考虑时空效应的泥岩隧道系统锚杆适用性数值分析
2022-04-20王勇杰李献民
王勇杰, 李献民
(1.河南交院工程技术集团有限公司,河南 郑州 450000; 2.中交一公局集团有限公司,北京 100024)
0 引言
新奥地利隧道施工法简称新奥法,于1960年由奥利地学者L.V.Rabcewicz 提出。其中,在隧道开挖后及时进行系统锚杆支护以控制隧道的变形是新奥法的具体措施之一,系统锚杆的主要作用是对隧道开挖周边的围岩松动区进行锚固,辅助隧道周边围岩承载[1]。目前,有关隧道锚杆的研究主要集中在锚杆的受力特性、单根锚杆理论计算和系统锚杆受力机理等方面,国内外工程界和学术界开展了相关的理论探索和技术革新[2]。陈建勋等[3]对不设系统锚杆的高含水量土质隧道进行了现场实测试验,结果表明,取消系统锚杆的隧道初期支护的结构变形和受力均在允许范围之内,对于高含水量土质隧道系统锚杆支护没有明显的支护效果,取消系统支护反而可以缩短工期。谭忠盛等[4]采用现场对比试验方法对深埋黄土隧道系统锚杆的作用效果问题进行研究,结果表明,拱部系统锚杆作用效果不明显,取消拱部系统锚杆可以减少工序,加快施工进度,节约工程投资。郭军等[5]通过理论推导、阐释了锚杆的作用,分析了浅埋大跨度黄土隧道中锚杆的受力性能,结果表明,浅埋黄土隧道中拱部系统锚杆的锚固效果较弱。章慧健等[6]通过数值模拟分析了隧道锚杆受力性能,结果表明,超大断面隧道锚杆轴力分布不均衡且拱顶锚杆轴力很小。陈建勋[7]采用 FLAC3D 建立软弱围岩隧道模型,通过对比多种工况下的隧道支护效果,认为取消拱部范围系统锚杆,不仅未影响隧道围岩稳定,而且可以缩短工序循环时间。李献民等[8]针对系统锚杆作用效果问题开展大量的现场试验,通过试验段测试得出,深埋泥岩隧道有无设置系统锚杆条件下围岩变形及受力都无明显差异,锚杆支护作用效果较差,取消系统锚杆不影响支护结构安全。陈力华[9]采用隧道稳定性定量计算方法对系统锚杆在黄土隧道中的效果进行了分析,结果表明,黄土隧道中设置系统锚杆对隧道整体稳定性影响不大,只有采用拱架支护才能有效地提高隧道的稳定性。刘洋等[10]以武西高速公路桃花峪隧道施工为依托,进行了有无锚杆现场对比试验,结果表明:锚杆对改善隧道围岩和初期支护受力作用相对较小,建议取消锚杆。
与上述结论相反,国内有些学者认为,在隧道中进行系统锚杆支护是新奥法必不可少的措施,具有不可替代的作用,尤其是在软弱破碎岩体中,系统锚杆可以提高岩体的完整性,从而起到加固隧道的结果,因此系统锚杆的效果不能忽视[11-13]。由此可见,对隧道系统锚杆的作用机理和使用条件业界缺乏统一的认识,对隧道锚杆的支护效果存在分歧。为了更好地研究系统锚杆在软岩隧道中的加固效果,依托贵州沿印松高速李家寨隧道工程,采用Midas软件建立了分析模型,对软岩隧道初期支护结构中的系统锚杆功效和适用性进行了分析,为软岩隧道设计和施工提供案例和依据。
1 考虑时间效应的模型实现及模拟工况
1.1 工程概况
李家寨隧道围岩为中风化泥岩、泥质结构、中厚层状构造,属IV级围岩。初期支护设计参数:I14型钢拱架,间距100 cm;φ6.5钢筋网,间距25 cm×25 cm;φ20药卷系统锚杆,长度为3.0 m,间距为100 cm×120 cm(纵×环),梅花形布置;20 cm厚C20喷射混凝土;二衬及仰拱为C30素混凝土,隧底填充采用C15混凝土。
1.2 数值计算模型
(1)几何模型
采用建模简便、网格划分少和计算速度快的二维数值模型进行仿真计算。由圣维南原理[14],隧道开挖对隧道周围3~5倍开挖宽度内岩体内应力应变产生影响,结合隧道正洞结构尺寸,二维平面应变几何模型宽×深尺寸为120 m×120 m。
(2)材料属性
本构关系方面,考虑围岩材料的弹塑性变形,采用摩尔-库伦准则[15];混凝土或钢材仅考虑其弹性工作范围,采用线弹性破坏准则[16]。网格单元类型,围岩视为连续介质采用平面应变单元模拟,初期支护C20喷射混凝土采用板单元模拟,锚杆采用植入式桁架单元模拟。
(3)荷载及边界条件
地表为自由面,其余各面均采用法向位移约束。初始应力场仅考虑自重应力场,不考虑围岩地层的构造应力场;由于地下水贫乏,不考虑地下水渗流场条件。图1给出了数值模拟分析的荷载边界条件和网格划分。

图1 数值分析模型
(4)材料物理力学参数
表1给出了隧道围岩与支护材料物理参数。
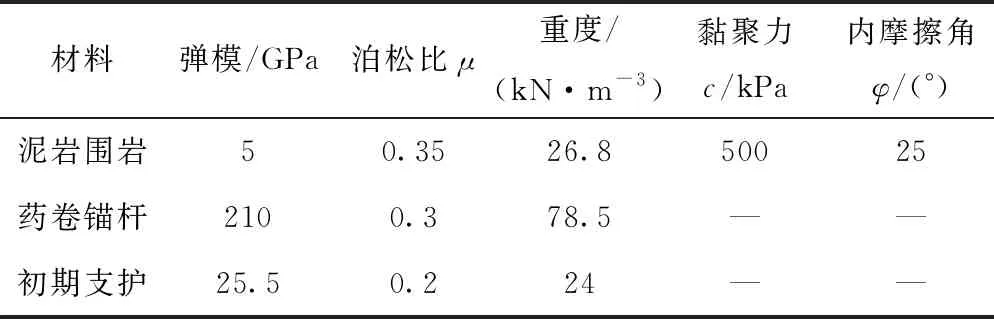
表1 材料性能
(5)数值模型修正验证
如图2所示,根据依托工程李家寨隧道试验段隧道断面特征点监测项目:围岩变形、锚杆轴力、C20喷射混凝土应力(可换算出初期支护轴力)的实测数据结果[8],反复修正所建立的2D平面应变数值计算模型,控制数值模型中参数计算结果与现场实测数据误差在±3%以内,以验证所建立的数值计算模型的合理性和适用性。

图2 隧道横断面特征点示意图
1.3 工况设计
(1)4种模拟工况
采用有限元软件Midas GTS进行数值模拟分析系统锚杆支护效果,重点考虑时间空间效应条件下,有、无设置系统锚杆情况下隧道围岩变形及初期支护结构受力机制,对比分析系统锚杆在软质围岩隧道初期支护结构中所发挥的作用效果。具体模拟工况分4种:工况1为有系统锚杆工况,工况2、工况3、工况4为取消系统锚杆工况。工况1系统锚杆布设范围180°,锚杆长度3 m,间距为100 cm×120 cm(纵×环),梅花形布置,其他设计参数与取消系统锚杆3个工况相同。
(2)考虑时空效应的施工阶段模拟
由于隧道开挖是一个应力释放的过程,具有显著的时空效应,通过设置应力释放率模拟隧道开挖过程中的时空效应。4种工况都采用两台阶开挖,但相应施工阶段应力释放率各不相同。比如,工况1为有系统锚杆的慢速支护工况,考虑时空效应的施工阶段模拟为:工序1为施工准备阶段,位移清零;工序2为上台阶开挖,应力释放40%;工序3为施作锚杆和上台阶初期支护,应力释放30%;工序4为下台阶开挖,应力释放30%;工序5为下台阶初期支护及仰拱施作,应力释放率为0,其他工况情况详见表2。
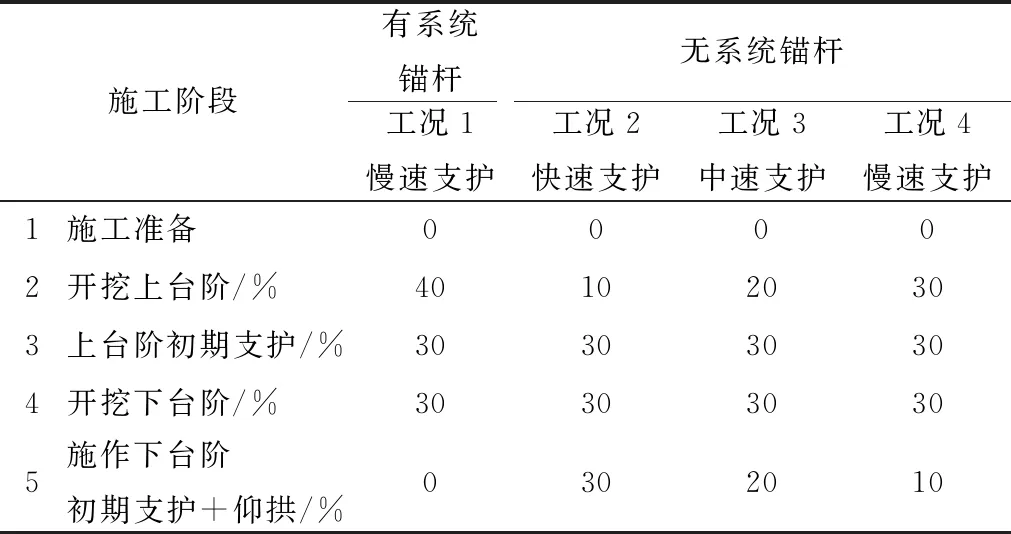
表2 考虑时空效应引起的应力释放率的模拟工况
2 隧道变形与结构受力分析
2.1 围岩变形总体特征
由图3可以看出各工况隧道围岩竖向沉降变形特征:(1)工况1~工况4拱顶下沉最大值分别为38.2,32.2 ,35.0 mm和37.8 mm,显示出隧道有无施作系统锚杆对围岩竖向沉降变形控制不显著。(2)初期支护时间越早,围岩应力释放率越小,围岩沉降变形越小,证明了取消系统锚杆可节省工序提高工效,及时进行初期支护可有效减少围岩竖向沉降变形。
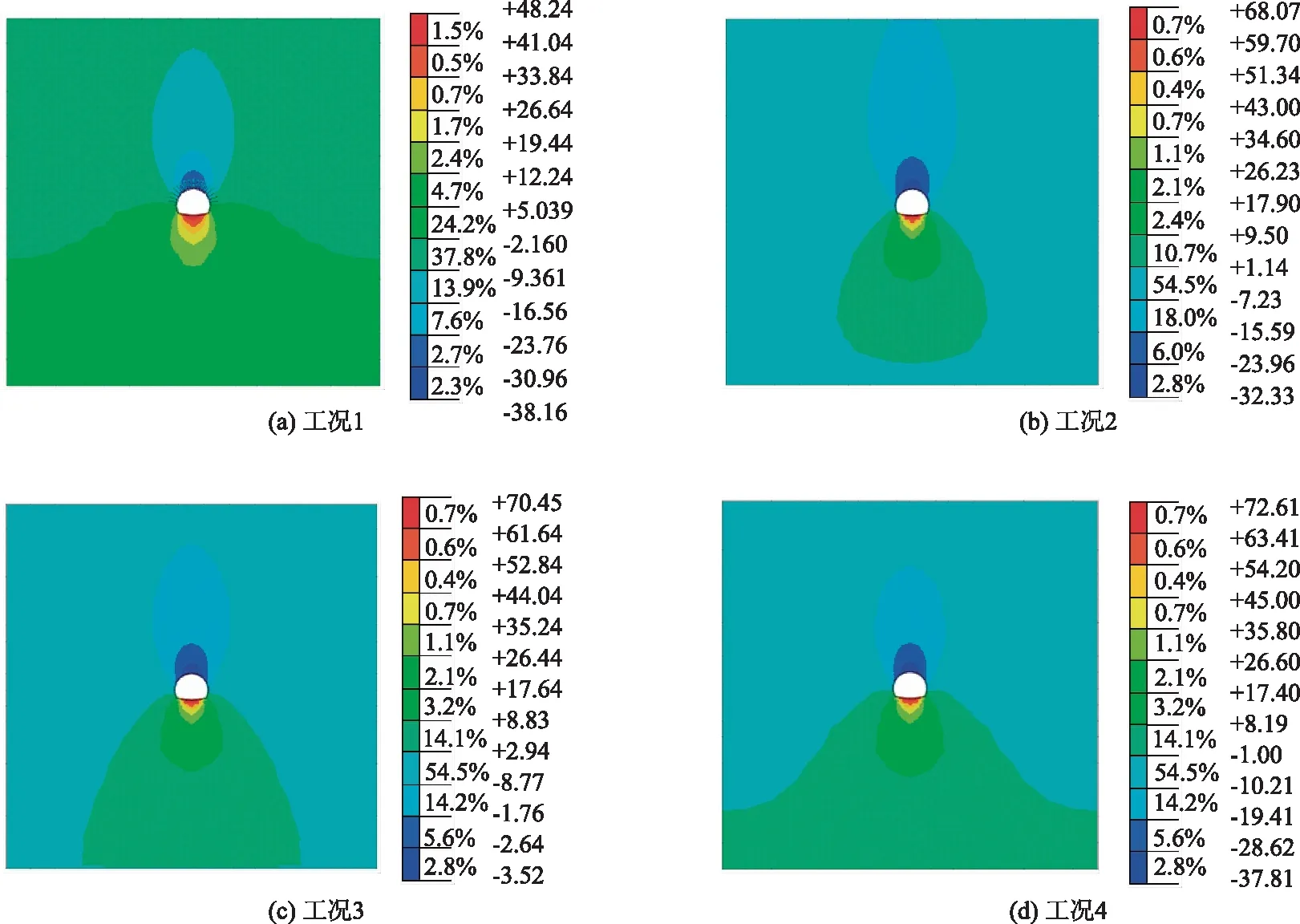
图3 各工况围岩竖向沉降变形云图(单位:mm)
由图4可以看出各工况隧道围岩水平收敛变形特征:(1)工况1~工况4水平收敛最大值分别为5.33,10.31,9.47 mm和9.07 mm,显示出施作系统锚杆能超到控制围岩水平收敛变形的作用。(2)初期支护时间越早,围岩应力释放率越小,围岩水平收敛会越大,且远大于工况1围岩的水平收敛,这是因为工况1中边墙系统锚杆起到了锁脚锚杆的作用,有效控制了围岩收敛。因此,如果取消系统锚杆,应加强隧道初期支护锁脚锚杆的施作。

图4 各工况围岩水平收敛云图(单位:mm)
2.2 隧道断面特征点变形
根据图5、图6及表3,不难看出围岩特征点变形特征。

表3 围岩特征点变形(单位:mm)

图5 各工况隧道各特征点变形
竖向沉降变形特征:(1)工况1拱顶(A点)、拱肩(B、C点)、拱脚(F、G点)竖向位移比取消系统锚杆3种工况对应特征点竖向位移稍大,最大极差达到5.9~6.6 mm;(2)工况1拱腰D、E点竖向位移比取消系统锚杆3种工况对应特征点竖向位移都小,最大极差达到9.4 mm。(3)除拱腰D、E点外,取消施作系统锚杆及时初期支护会减小竖向位移,且拱腰D、E点竖向沉降变形受时空效应影响显著。
水平收敛变形特征:(1)工况1拱肩(B、C点)大,最大极差达到1.7~2.0 mm。(2)工况1拱腰(D,E点)、拱脚(F,G点)水平位移比取消系统3种工况对应特征点水平位移都小,最大极差达到6.9 mm,原因是工况1拱腰系统锚杆起到了锁锚杆作用,控制制围岩水平收敛,取消系统锚杆,应加强初支锁脚锚管的施作。(3)除拱肩特征点B、C外,施作系统锚杆会减小隧道水平位移,且拱腰D、E点水平收敛变形受时空效应影响显著。
2.3 初期支护轴力
根据图6~图7得到初期支护轴力表现有如下特征:(1)4种工况初期支护受到的轴力都是压力,所受轴力极值大小分别为:-913,-3 263,-2 831,-2 462 kN,取消系统锚杆工况初期支护轴力显著大于施作系统锚杆工况,更有利于控制隧道结构受力、围岩变形和塑性区发展。(2)取消系统锚杆3种工况随着初期围岩应力释放率增大,初期支护轴力呈现出减小趋势。由于隧道开挖围岩应力时空效应引起原始应力重新分布,若支护时间过早,初期支护结构需要承担部分松动围岩荷载,从而导致初期支护结构轴力增大。(3)初期支护施作时间越早,初期支护受到的轴力越大。因此,取消系统锚杆首先必须保证初期支护强度,其次要根据新奥法施工理念和围岩地质岩性条件选择初期支护最佳施作时机[17]。

图6 各工况初期支护轴力峰值柱状图

图7 各工况特征点初期支护轴力
2.4 围岩塑性区
从图8可以看出,隧道开挖时空效应条件下围岩塑性区发展表现出以下特征:(1)相对于取消系统锚杆3种工况,施作系统锚杆工况对围岩塑性区发展控制效果较明显。(2)取消系统锚杆3种工况,随着初期围岩应力释放率的变大,围岩塑性区范围依次变大,说明隧道开挖应力释放过程时空效应显著,越早进行初期支护和封闭成环,对塑性区范围大小及其发展的控制越有利。

图8 各工况围岩塑性区云图
2.5 初期支护安全系数计算
按破损阶段验算构件截面强度应根据不同荷载组合并分别采用不同的安全系数K,见表4[18]。
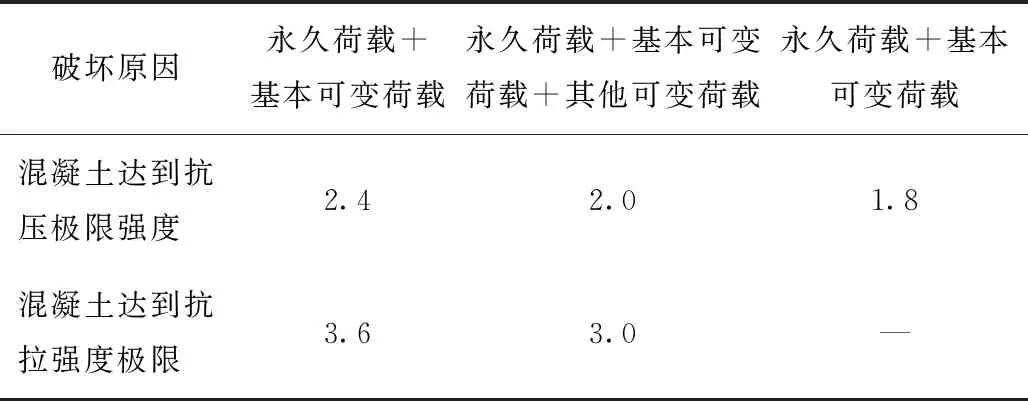
表4 混凝土结构各种荷载组合的强度安全系数
(1)隧道衬砌混凝土矩形截面轴心及偏心受压构件的抗压强度计算为:
KN≤φαRabh,
(1)
式中,K为安全系数,见表7;N为轴向力;φ为构件的纵向弯曲系数,对于隧道衬砌、明洞拱圈及墙背紧密回填的边墙可取φ=1,对于其他构件应根据其长细比选用[18],取φ=1;Ra为混凝土或砌体的抗压极限强度;b为截面宽度,取1 m;h为截面厚度,取0.2 m;α为轴向力偏心影响系数[18]。
(2)按抗裂要求,混凝土矩形截面偏心受压构件的抗拉强度计算为:
(2)
式中,R1为混凝土的抗拉极限强度,取R1=1.7;e0为轴向力偏心距。
(3)工况特征点强度及安全系数计算
根据破损阶段法验算安全系数,在最不利荷载组合的作用下,结构的控制内力不超过材料的极限承载力,即:
(3)
李家寨隧道安全系数验算结果见表5,未施作系统锚杆3种工况安全系数均满足规范要求。

表5 工况特征点安全系数计算数据
3 结论
(1)系统锚杆在中厚层泥岩隧道支护结构中的功效不明显且不适用。
(2)考虑时空效应因素条件,取消系统锚杆更有利于控制隧道结构受力、围岩变形和塑性区发展。
(3)泥岩隧道不施作系统锚杆工况计算结果表明,其初期支护安全系数满足规范要求,取消系统锚杆技术在安全上可行。
(4)取消系统锚杆应加强边墙锁脚锚杆施作和保证初期支护早期强度以利于有效控制围岩沉降收敛变形。
(5)软岩隧道支护结构系统锚杆的优化和取消,应经过现场试验段工程验证或工程类比分析验算后才可以推广应用。
