超高车辆-预应力混凝土箱梁桥碰撞荷载分析及撞后承载力评估

2022-04-20邹育麟邹品德张景峰

公路交通科技 2022年3期

邹育麟，邹品德，申鹏,3，张景峰

(1. 四川沿江攀宁高速公路有限公司，四川攀枝花 617112；2. 四川路桥桥梁工程有限责任公司，四川成都 610017； 3. 四川省交通建设集团股份有限公司，四川成都 610041； 4. 长安大学公路学院,陕西西安 710064)

0 引言

近些年，随着交通运输事业的飞速发展，桥梁遭受车辆、船舶等极端荷载冲击情况时有发生[1-2]。2019年5月18日，杭州庆春路人行天桥受运输盾构设备的超高车辆撞击，导致天桥落梁垮塌。虽然超高车辆撞毁跨线立交桥梁的概率较小，但其对受撞梁造成的损伤不容忽视，尤其是预应力筋在撞断失效情况下，存在极大的安全隐患。

目前，在桥梁结构遭受撞击的问题研究方面，船舶撞击桥梁的理论已较为成熟[3-5]。而车辆撞击桥梁的研究主要集中于桥墩[6-7]以及护栏[8]的抗撞性能及损伤破坏机理等方面，针对桥梁上部结构在超高车辆撞击下的问题研究则相对较少。陆新征等[9]基于精细化非线性有限元和事故案例分析，研究了不同车型撞击桥梁上部结构的损坏机理与撞击荷载；田力等[10]通过数值仿真研究了预应力混凝土箱梁桥在超高车辆撞击下的动态响应问题；张炎圣等[11]基于有限元仿真，建立了超高车辆-桥梁上部结构碰撞的简化计算模型；彭卫兵等[12]基于现场残骸和碰撞痕迹对杭州庆春路人行天桥在超高车辆撞击下的倒塌原因进行了深入分析；叶志雄等[13]基于数值仿真，研究了LRB隔震桥梁在超高车辆撞击下的整体响应问题。既有研究中采用的车辆模型大多为美国国家碰撞分析中心(NCAC)提供的8 t标准双轴卡车有限元模型[14]，而对于结构在重型货车(车重大于12 t)撞击下的损伤特征研究较少。此外，现有文献侧重于研究结构在车辆撞击荷载下的损伤机理分析，而对于碰撞荷载及结构损伤后承载力的劣化规律研究不足。

在城市以及高速路的跨线工程中，预制装配式箱梁桥应用广泛，其遭受超高车辆撞击情形时有发生。桥梁结构在碰撞荷载作用下，其损伤程度与荷载大小、荷载持时及其随时间的变化规律等因素密切相关，然而目前世界各国对桥梁的防撞设计均基于风险分析的等效静力设计法。我国规范参考国外桥梁设计规范规定：桥梁受到车辆撞击时，汽车撞击力设计值沿车辆行驶方向取1 000 kN，与车辆行驶垂直方向取500 kN，且两个方向撞击力不同时考虑，撞击力作用于行车道以上1.2 m处，直接分布于撞击设计的构件上。本研究采用LS-DYNA显式动力分析软件，对预应力混凝土箱梁桥在超高车辆撞击下的碰撞荷载及撞后结构竖向极限承载力进行了研究。通过将荷载时程曲线简化处理，分析了不同计算参数对4个关键指标(碰撞力峰值、碰撞力均值、均值力持时和碰撞冲量)的影响，为进一步建立碰撞荷载的简化计算模型提供参考。同时，为对比不同撞击荷载下结构的损伤程度，计算了被撞梁损伤后的竖向极限承载力，进而为结构的修补加固提供合理参考。

1 数值模型及模型验证

1.1 有限元模型

本研究参考文献[15]建立了典型预应力混凝土箱梁桥上部结构的有限元模型。桥梁标准跨径为30 m，全桥由5片预应力混凝土小箱梁组成，桥面宽14.6 m。主梁采用C50混凝土；预应力钢筋采用φ15.2 mm高强、低松弛钢绞线，张拉控制应力为1 395 MPa。除底板纵向钢筋为φ16HRB335外，普通钢筋均采用φR235。桥梁上部结构有限元模型如图1所示。

图1 桥梁有限元模型

车辆模型以美国国家碰撞分析中心(NCAC)发布的标准双轴卡车模型为原型，建立了该车辆的简化有限元分析模型。简化模型在准确模拟车厢尺寸、刚度、材料特性以及车重的基础上，结合我国车辆实际情况，将其改装成以“楚风前四后八厢式运输车”为原型的超高车辆有限元模型。该车整备质量12.8 t，满载时总质量31 t。在后续的分析计算中均采用改装后的车辆模型。车辆有限元模型如图2所示。

图2 车辆有限元模型

1.2 单元类型及材料本构

为提高分析效率，混凝土及支座单元均采用缩减积分8节点三维实体单元模拟。普通钢筋及预应力钢筋采用Hughes-Liu梁单元进行模拟。车厢采用基于Belytschko-Tsay算法的薄壳单元进行模拟，碰撞区域网格最小尺寸为10 cm。

与静载作用相比，结构在冲击作用下的材料应变率效应不容忽视，该效应可导致材料的强度、延性以及破坏模式发生较大改变。混凝土材料采用能够模拟其在低速冲击下的弹塑性变形以及失效行为的连续光滑帽盖模型进行模拟，其应变率效应通过黏塑性应力更新算法实现；壳单元采用分段线性材料模型(*MAT_PIECEWISE_LINEAR_PLASTICITY)进行模拟，通过定义材料在碰撞作用下的应力应变曲线来考虑其应变率效应。普通钢筋采用双线性弹塑性随动硬化模型(*MAT_PLASTIC_KINEMATIC)，失效应变设置为0.12，普通钢筋和车厢材料的应变率效应均采用Cowper-Symonds模型[8]进行计算。预应力筋单元采用*MAT_ELASTIC_PLASTIC_THERMAL材料模型，预应力荷载通过等效降温法进行模拟。

1.3 模型验证

根据足尺试验得到的预应力混凝土箱梁桥单梁在竖向荷载作用下跨中的荷载-位移曲线及裂缝开展规律，对本研究建立的桥梁有限元模型进行验证。图3给出了试验梁跨中位置的荷载-位移曲线。可以看出，竖向荷载下二者的位移变化规律相同，且在临近极限竖向荷载时，数值模型与足尺试验的跨中竖向位移吻合程度较高。结合文献[13]中对裂缝开展过程的描述：在750 kN的竖向荷载作用下，跨中附近腹板首先出现自底缘向上的竖向裂缝(长度约9.2 cm)；随着竖向荷载的持续增加，裂缝数量逐渐增多，裂缝宽度不断增大；当荷载达到1 700 kN(临近极限荷载)时，裂缝宽度迅速增加；在试验终止时，箱梁最大裂缝宽度达到6 mm，均分布在距跨中8 m范围内。图4给出了按照足尺试验布载方式下主梁跨中塑性损伤区域的演化过程。可以发现，主梁在竖向荷载作用下的塑性损伤开展过程及分布规律与足尺试验结果基本吻合。这说明本研究建立的桥梁有限元模型可以较好地反映其在实际荷载下的工作性能。

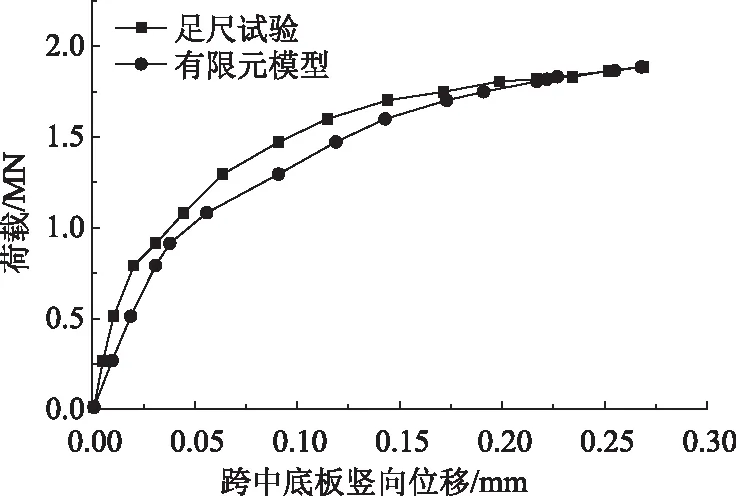
图3 主梁荷载-位移曲线

图4 竖向荷载下主梁塑性损伤区域演化过程

美国国家碰撞分析中心(NCAC)以碰撞试验为基础建立的标准双轴卡车模型，其模拟碰撞行为的有效性已得到众多研究者的验证[16-17]。本研究对比了简化模型和标准双轴卡车模型与结构碰撞后的计算结果。从图5(a)中可以看出，二者的碰撞力时程曲线变化规律基本保持一致，并且峰值力及荷载持时相差不大。图5(b)给出了桥梁受撞击位置沿行车方向的位移变化曲线。在两种车辆的撞击作用下，结构的动态响应基本相同。主梁损伤区域的分布情况如图5(c)所示。在两种车辆模型的碰撞作用下，受撞梁塑性损伤区域分布基本一致，损伤范围集中于碰撞位置附近的箱梁腹板及顶板与腹板交界位置处，并且碰撞点均出现了混凝土剥落及钢筋外露现象。由此可见，本研究建立的简化车辆模型可以用来模拟车-桥碰撞行为，并且计算结果具有一定的可信度。

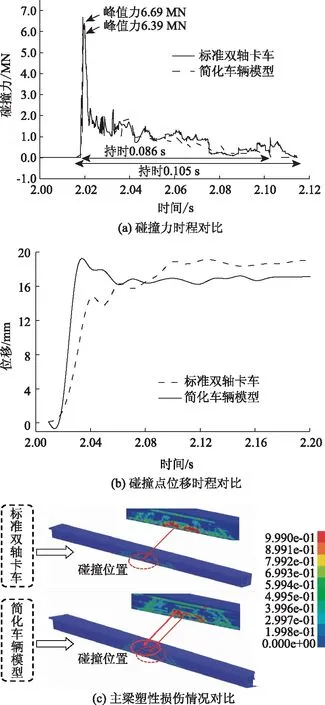
图5 简化车辆模型有效性验证

2 超高车辆-箱梁桥碰撞荷载

2.1 分析参数设定及计算工况说明

超高车辆与箱梁桥上部结构碰撞计算过程共历时2.4 s，具体可分为以下2个阶段：(1)初应力加载阶段:结构的自重、预应力荷载及二期恒载在这一阶段施加，持时2 s；(2)车-桥碰撞阶段:持时0.4 s，并选取边梁跨中作为车-桥典型碰撞位置。

本研究选取车辆速度、载重量、碰撞超高、车厢刚度、撞击角度以及主梁混凝土强度作为主要分析参数，研究了不同参数取值对撞击力峰值、均值力、均值力持时以及撞击冲量的影响，各工况参数取值见表1。考虑到货物的刚度差异较大，本研究暂不考虑其对主梁损伤的影响，仅考虑车厢与主梁的接触碰撞行为。

表1 工况参数

2.2 碰撞力、碰撞冲量及能量转化

2.2.1 碰撞力时程

图6给出了典型工况下(工况C3)的撞击力时程曲线。从图中可以看出，碰撞荷载随时间呈现明显的三阶段变化特征：碰撞初期，车厢与受撞梁腹板接触的瞬间，撞击力在短时间内迅速达到峰值，之后又迅速衰减至较低的水平；碰撞中期，由于材料非线性、接触非线性以及车厢的不均匀变形等因素影响，受撞梁受到的碰撞力在一定范围内不断波动，并且该阶段持时较长；碰撞末期，随着车厢塑性变形的增大，其与被撞梁接触面积逐渐减小，碰撞力呈下降趋势，最后衰减至0，车桥碰撞结束。基于以上分析和既有研究[18-19]，本研究将撞击力时程曲线简化为如下3个阶段：(1)突变阶段：车厢与受撞梁腹板接触瞬间，碰撞力短时间内增至峰值，之后又迅速衰减至较低水平。在该阶段内基于峰值力不变的原则，近似用三角形脉冲荷载代替突变阶段内的碰撞力；(2)振荡阶段：该阶段内碰撞力在一定范围内不断波动，持续时间相对较长，结构的损伤及变形主要在该阶段发生。为便于研究该阶段碰撞荷载的特性，基于荷载持时及碰撞冲量不变的原则将碰撞力时程曲线按矩形脉冲荷载的形式近似代替；(3)衰减阶段：在车桥碰撞的末期，碰撞力不断减小，最后衰减为0。基于第2阶段简化原则，将该阶段的碰撞力时程近似用三角形脉冲荷载替代。

图6 碰撞力时程及其简化曲线

由动量定理可知，任意时刻(0～t3内)撞击冲量I，撞击力F撞击时间t可用式(1)～(3)进行表示：

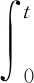
(1)

(2)

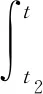
(3)

式中，Itri为突变阶段三角形脉冲荷载产生的冲量;Ivib为振荡阶段矩形脉冲荷载产生的冲量。分别可以用式(4)～(5)表示：

(4)

(5)

基于以上分析，突变阶段的撞击冲量主要由撞击力峰值及荷载持时决定，但各工况下该阶段持时往往较短(一般维持在0.01 s左右)，故撞击力峰值对撞击冲量的变化更为敏感；振荡阶段的撞击冲量除均值力起决定因素外，各计算工况下该阶段的荷载作用时间差异较大，因此荷载持时也是不可忽略的因素；衰减阶段的持时相对较短且荷载值不大，并且结构的损伤及变形在该阶段之前已基本完成，本研究暂不考虑该阶段的撞击影响。因此在以下分析中主要选取不同工况下突变阶段和振荡阶段的碰撞力峰值、碰撞力均值、均值力持时(振荡阶段)及碰撞冲量(前两个阶段之和)4个关键指标进行分析。

2.2.2 参数敏感性分析

图7中给出了不同速度、质量和碰撞高度下简化碰撞力时程曲线的关键指标值。可以发现，碰撞力冲量并不随着碰撞速度、碰撞质量和碰撞高度单调增长；随着碰撞速度的增大，碰撞力峰值基本呈线性增加，而其他计算参数对碰撞力峰值无明显影响；车辆速度、车辆载重和碰撞高度改变均会引起碰撞力均值以及均值力持时的较大变化。

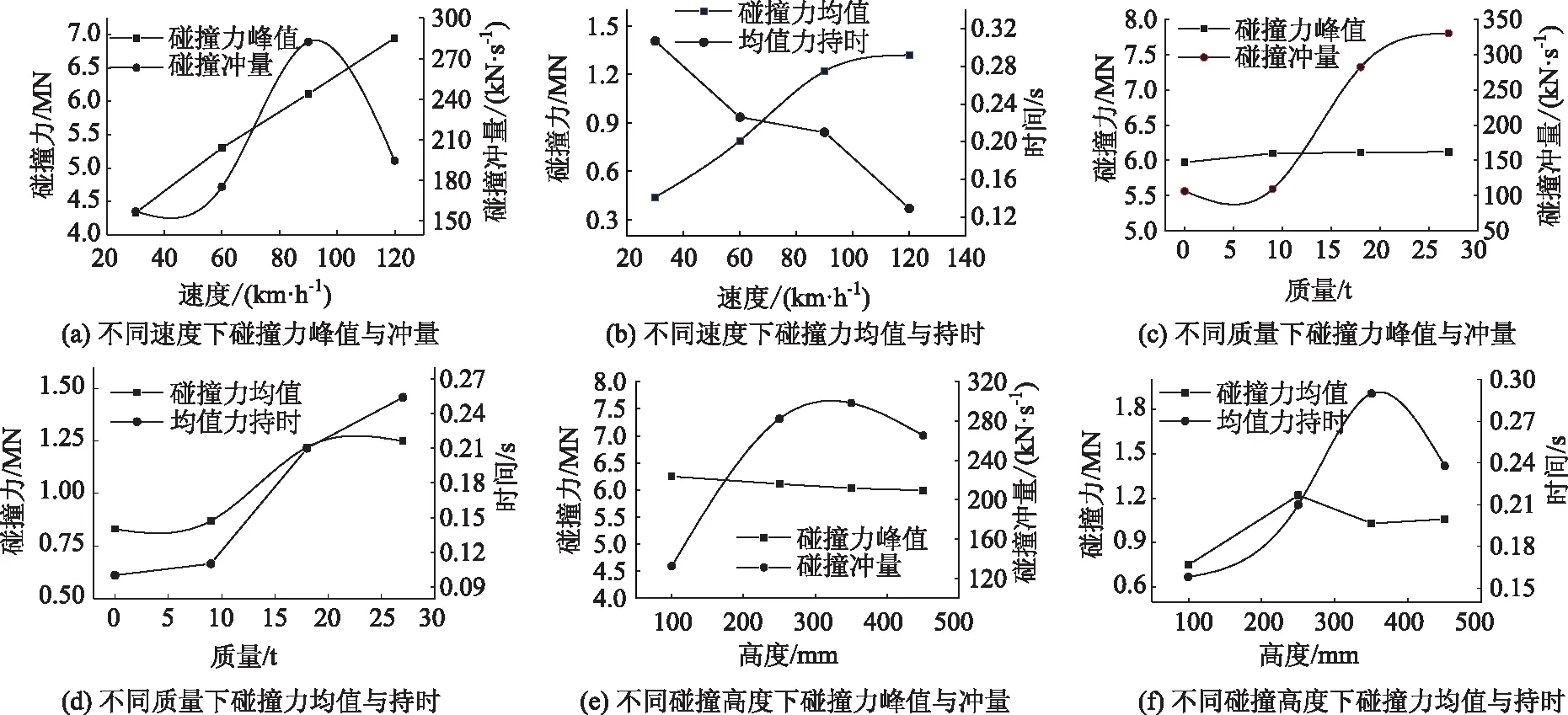
图7 不同碰撞速度、质量和高度下碰撞力关键指标值对比

2.2.3 碰撞冲量变化及能量转化

工况C1～C4碰撞过程中的冲量变化如图8所示。在初始碰撞阶段，由于不同速度下峰值力变化较大，导致撞击冲量有一定差别，但此时撞击冲量值均较小，整体差距不明显，随时间变化基本保持一致的增加速度；随着碰撞时间的推移，由于不同工况下的碰撞力及碰撞持时有较大差别，碰撞冲量的大小及增幅表现出较大不同；碰撞结束后，4种工况下冲量大小顺序：90 km/h>120 km/h>60 km/h>30 km/h。通过对碰撞过程进行分析，发现当车速在120 km/h时,车辆与主梁碰撞瞬间，车厢由于较强的局部冲击力作用而发生严重的塑性变形，车辆行驶速度大幅降低，并且在随后的碰撞过程当中与主梁的碰撞形式以冲切撞击为主，对结构的正面冲击能力减弱，此时的碰撞力及荷载持时出现较大变化，碰撞持时显著小于其他工况，导致其在碰撞结束后的碰撞冲量显著低于90 km/h下的冲量值。在工况C1～C3下，随着碰撞速度的增大，系统的输入能量亦增加，碰撞结束后碰撞冲量不断增大。图9给出了工况C1～C4碰撞后的能量对比。随着碰撞速度的提高，碰撞后车辆的残余动能的比例亦随之增大，而碰撞内能呈逐步下降趋势。可以发现，在碰撞过程中，碰撞前的能量大部分转化为系统内能(车厢及撞击区域混凝土的塑性应变能)和车辆的动能，其中车厢的塑性应变能是超高车辆撞击主梁的主要耗能机制，占总内能的比例达到90%以上，系统能量仅有少量以滑移能和沙漏能的形式耗散。

图8 工况C1～C4碰撞冲量对比

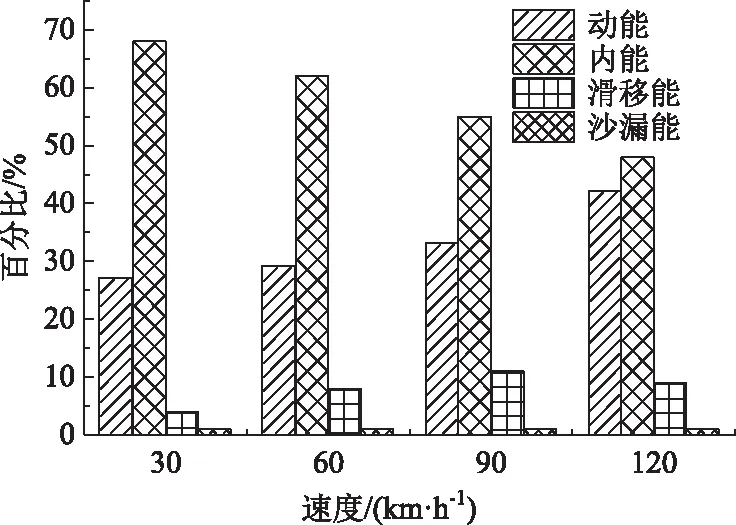
图9 工况C1～C4碰撞后能量耗散对比

3 被撞梁损伤分析及承载力评估

3.1 评估方法

桥梁上部结构受到车辆撞击后，除小跨径人行天桥外，其他跨线立交桥梁出现落梁破坏或者整体垮塌的概率较小。此时，被撞梁实际的承载性能很难通过结构损伤的分布范围及严重程度给出定量评估。本研究利用LS-DYNA的重启动功能，通过给被撞梁施加均匀增大的车道荷载来判断结构的实际剩余承载力。具体分析步骤为：(1)应力初始化阶段：在完成第2节中超高车辆撞击箱梁桥的损伤分析后，删掉除被撞梁及支座之外的其他无关单元组件，采用LS-DYNA中的*STRESS_INITIALIZATION命令进行应力初始化，使被撞梁单元继承上一阶段的损伤及变形，持时0.6 s；(2)竖向静力加载阶段：对损伤后的主梁施加随时间线性增大的公路Ⅰ级车道荷载，加载至主梁破坏结束，分析时长设定为1.5 s。

3.2 被撞梁损伤分析

图10给出了工况C1～C4下碰撞后主梁塑性损伤云图。随着碰撞速度的增大，被撞梁的塑性损伤范围逐渐扩大，损伤区域主要集中于碰撞区域腹板、腹板与顶板连接处、底板以及撞击区域另一侧腹板。在车辆行驶速度为30 km/h和60 km/h下，主梁仅撞击区域及腹板与顶板连接处，混凝土由于车辆的冲击作用出现轻微塑性损伤，未出现混凝土剥落及露筋现象。当车辆行驶速度达到90 km/h和120 km/h时，被撞梁撞击区域塑性损伤明显，局部出现混凝土剥落、普通钢筋外露及屈服现象，并且塑性损伤区域向梁端扩展明显，损伤范围明显大于工况C1和C2；此时，箱梁未受撞击侧腹板及顶板与腹板连接处由于局部弯剪作用出现较为严重的塑性损伤，在工况C4下出现了明显的斜向塑性发展区。

图10 工况C1～C4碰撞后主梁塑性损伤云图

工况C1～C4下桥梁上部结构的整体位移和变形如表2所示。与简支T梁桥及钢箱-混凝土板组合梁桥相比[9]，预应力混凝土箱梁桥在超高车辆撞击下的整体位移及变形较小，由此引起桥梁上部结构损伤并不明显。考虑到结构的整体位移及变形与结构的自重关系较大，本研究中的箱梁桥上部结构重629 t，远远超过车辆的质量。此外，箱梁桥底板厚度为180 mm，与车辆的超高值250 mm较为接近，可见直接冲击区域大部分都集中于箱梁底板范围内，相对于腹板，底板侧向抗弯刚度较大，承受冲击能力更强，在车辆的碰撞作用下产生的水平弯曲变形较小。

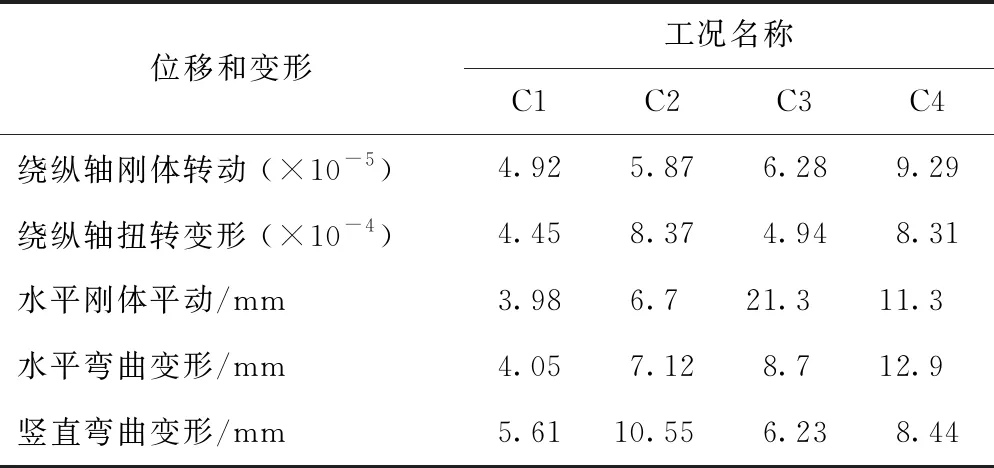
表2 桥梁上部结构整体位移和变形

3.3 被撞梁竖向承载力分析

图11中给出了不同车速撞击下被撞梁损伤后的荷载-位移曲线。工况C1～C4下曲线的变化规律基本保持一致，与结构损伤前相比，竖向极限承载力下降程度较低。按照同样的计算方法，计算了其他碰撞参数下被撞梁的竖向极限承载力，各工况下的竖向极限承载力见表2。为便于对比不同工况下竖向承载力的下降程度，图12给出了不同损伤工况下被撞梁的竖向剩余承载力百分比。总体上表现出结构的损伤越严重，结构的竖向剩余承载力越低的变化规律。可以看出，除工况C7，C13和C14外，结构的竖向极限承载力下降有限，都维持在10%以内。其中，工况C13下被撞梁的竖向承载力损失最为严重，但下降程度仅有18%。由此可见，对于预应力混凝土箱梁桥而言，在车辆撞击引起腹板局部损伤(混凝土剥落、普通钢筋屈服)下，对结构的竖向极限承载力及竖向变形刚度影响有限。

图11 主梁损伤后竖向剩余承载力

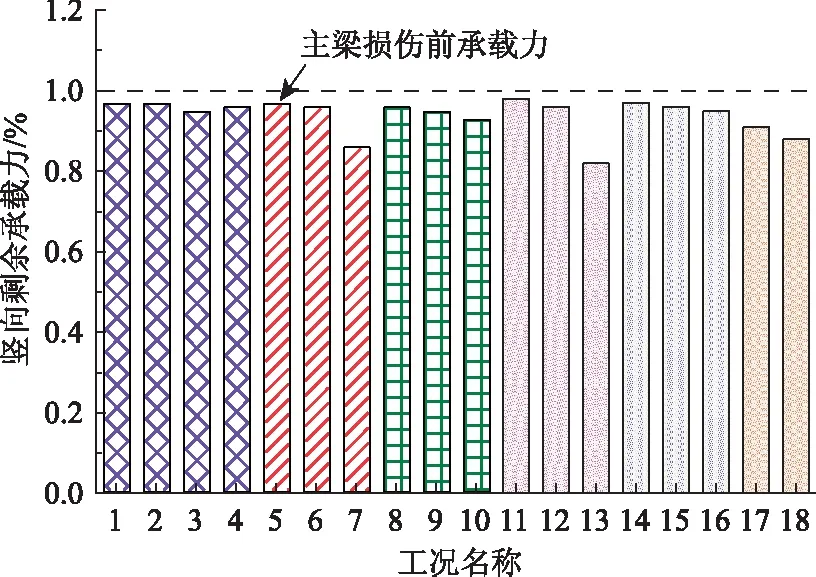
图12 工况C1～C18下被撞梁竖向剩余承载力

然而，在极端工况下(工况C7，C13)，超高车辆撞击很有可能引起主梁预应力钢束屈服断裂，进而退出工作，如图13所示。偏安全起见，在模拟中预应力筋一旦产生明显的塑性变形，本研究即认为其已退出工作，在竖向承载力分析过程中，将该预应力钢束单元删除。为研究预应力筋失效对结构竖向极限承载力的影响程度，分别计算了如图11所示的不同数量预应力筋失效情况下结构的荷载-位移曲线(P1,P2,P3,P4分别代表不同的预应力钢束，见图1)。当预应力筋屈服失效后，结构的竖向极限承载力及加载过程中的竖向抗弯刚度均发生明显下降。在撞击侧4根预应力束筋完全撞断失效的情况下，结构的竖向极限承载力仅为损伤前的46%，损伤程度达到一半以上。同时，结构在自重及二期荷载下就会产生明显的下挠，由此可见，对于预应力混凝土箱梁桥而言，一旦预应力钢筋受到撞击退出工作，结构的工作性能就会发生大幅衰减。