基于ANSYS 的多相输油管道弯管内流场数值模拟研究

赵盼婷，王素梅，文 杰

（中国石油长庆油田分公司第三输油处，宁夏银川 750006）

为改变流体输送方向，在管道转弯处常采用具有一定曲率半径的弯头，一方面弯头的连接使管道易于变形，但另一方面，由于弯头处压力与速度发生了极大的变化，使弯头处发生冲蚀磨损的概率往往比直管高很多[1]。分析弯径比、弯头数量对弯管流场的影响，确定最佳范围弯管参数，同时量化弯管处多相流的流动特性，分析油相及水相分布对于管道的优化设计及指导输油管道安全运行至关重要。

1 流体理论基础

1.1 控制方程

弯管中的多相流体各相之间在宏观尺度上混合，该混合尺度远小于网格尺度，但是远大于分子尺度。所有的相占有同一空间体积，在控制体内假设每一相占有的体积大小用变量体积分数来表示；每一相有自己的流场参数，各相通过相间的能量传输、动量传输、质量传输模型耦合，每一相具有各自的质量、动量、能量传输方程[2]。三维空间坐标下，混合介质遵循的控制方程如下：

（1）连续性方程：

式中：ρ－混合物料密度；uj－不同方向上的速度分量；Sm－质量源总和，满足质量守恒时有Sm=0。

（2）动量方程：

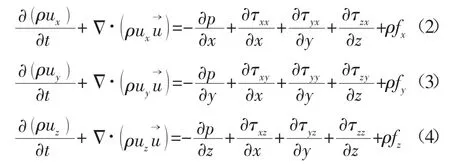
式中：p－作用在控制体上的压力，Pa；∂τxx、∂τyy、∂τzz－不同方向黏性应力τ 的分量，Pa；fx、fy、fz－质量力在不同方向的分力，m/s2。

（3）能量方程：

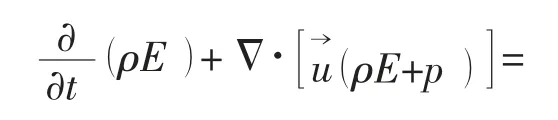
式中：E－系统的总能量，J/kg；hj-组分j 的焓，J/kg；T-流体温度，Tref=298.15 K；keff-热传导系数，W/（m·k），keff=k+ke；Jj-组分j 的扩散通量；sh-内热源项。

1.2 湍流模型

多相混合介质在弯管处速度急剧发生变化，由于速度的变化引起介质浓度、动量、能量的变化，此处的瞬时流场较为复杂，伴随随机性、扩散性、有涡性和耗散性，因此本文采用湍流模型对弯管内流场进行分析。其中的湍动能k 方程和耗散率ε 输运方程如下所示：

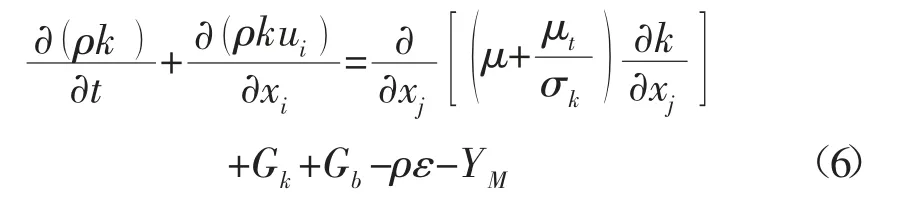
式中：Gk-平均速度梯度造成的湍动能生成；Gb-由于浮力影响引起的湍动能产生，对于不可压缩流体，在本研究中，流速比较低，故Gb=0；YM-可压缩湍流脉动膨胀对总的耗散率的影响，对于不可压缩流体，YM=0。

2 数值计算方法

2.1 建立模型及网格划分

确定弯管内流体遵循的流体控制方程后需建立数学模型对流体单元进行模拟分析。本文研究目标选取油房庄生产运行库站内手动进罐管线新老站连头处弯管作为研究对象，该管段使用DN350 的90°弯头，管道外径377 mm，壁厚10.5 mm。初始模型由三部分组成：进口直管段a=1 m、弯管半径R=0.356 m、出口直管段b=1 m。应用SolidWorks 软件建立初始模型后用Mesh软件进行网格划分。根据多相介质流动特性合理划分网格，弯管弯曲区域物理量变化剧烈需对网格适当加密，使得模拟结果与实际更吻合[3]。网格划分参数及方法（见表1）。

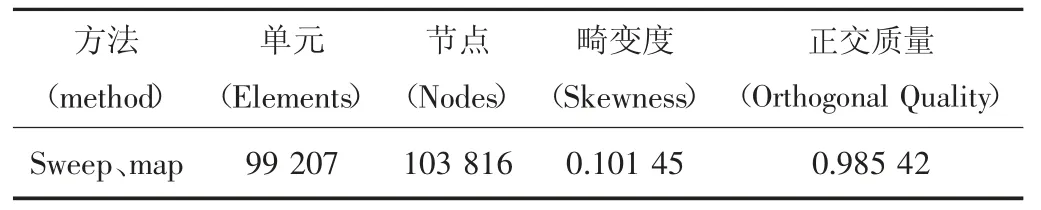
表1 网格划分

2.2 条件设置

多相流输油管道弯管内流体物性参数（见表2），模拟时需要假设：从入口进入的流体在管道内的流动属于稳态；切向入口处的流体流动速度一致且均匀；模拟过程中流场温度稳定[4]。根据管道尺寸所得水力直径DH=0.356，湍流强度I=5.4%。取油房庄生产运行库2021 年1 月1 日8:00 时，手动进罐管线的平均瞬时流量Q=423.5 m3/h 模拟。此时的平均流速为1.2 m/s，管道入口设置为速度入口（Velocity inlet），管道出口设置为自由出口（outflow），管壁设置为无滑移（no-slip wall）。

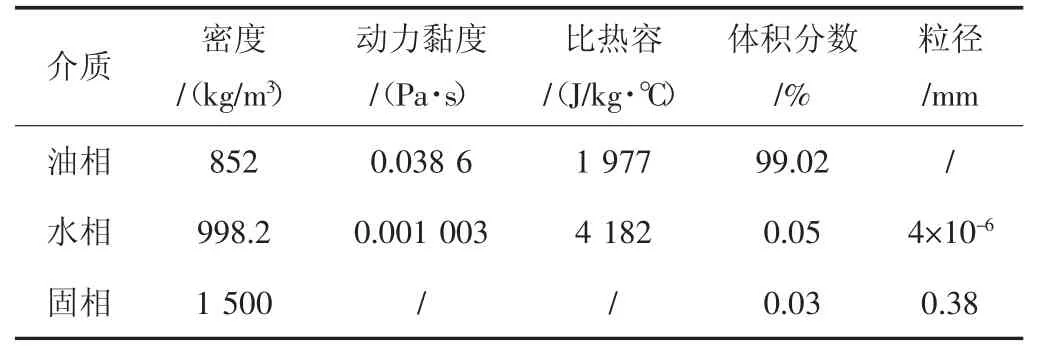
表2 介质物性参数

求解过程选择压力求解器，多相流模型选择mixture 混合模型，湍流方程选择标准k－ε 方程。压力与速度耦合算法选择SIMPLEC 方法，压力插补格式选择PRESTO 格式，动量及湍动能离散化采用二阶迎风（Second Order Upwind）的离散格式，体积分数离散化采用QUICK 格式。

3 数值模拟及结果分析

取Z=0 的截面分析多相流弯管处的压力与速度云图（见图1），从图1（a）压力云图可以看出流体在直管段压力均匀分布，流经弯头时内侧负压，外侧压力增至最大值，弯头断面上压差在弯头弯曲的顶点达到最大值，多相流体在出口直管段压力又恢复平稳。从图1（b）可以看出多相流体速度从弯头外侧到内侧速度值先增大后减小，在近壁面处由于摩擦阻力的影响，速度值近似为零。出现这种现象的原因主要是多相流体在流经弯头处时受离心力作用，而弯头内弧面较外弧面为短半径，因此靠近内弧面处速度增大[5]。压力分布与速度分布呈现相反趋势，因为大量流体流经弯头时被甩向曲率半径较大的外壁面，使得动能转化为压力势能，使得压力势能在外壁面有最大值。

图1 90°弯头压力与速度分布云图

从图2 弯头处的冲蚀磨损速率图可以看出，多相流体在除弯管外侧壁面的区域冲蚀速率基本不变，主要由于流体从管道入口流入后其流动方向与管道轴线平行，对管壁几乎没有冲击，当流经弯头处时管道几何形状改变，流体方向发生变化，受弯头外弧面较大压力的作用，此处的流体对该区域的冲击力也最大[6]，因此冲蚀速率最高的点分布在弯头外侧，本文所研究流体速度较低，固体杂质颗粒较少，因此冲蚀区域较小。

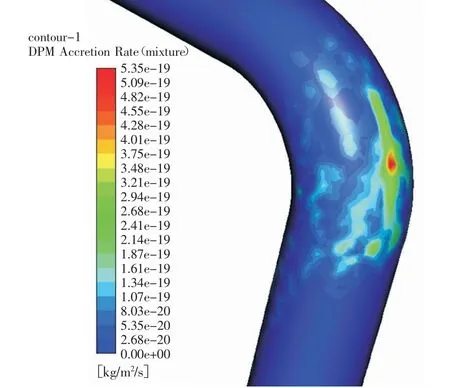
图2 90°弯头冲蚀速率云图

3.1 弯径比对弯管内流场的影响

为研究多相流体流经弯径比不同的弯管时内部压力与速度分布规律及弯径比对冲蚀速率的影响，建立弯径比R/D 为1、1.5、2、3 的弯管模型。取弯头处同一直线分析不同弯径比的弯管静压与速度分布，从压力分布曲线图（见图3）可以看出弯径比越小时，弯头内外侧压差越大，而此时的速度增至最大。从冲蚀磨损速率表中可以看出（见表3），随着弯径比的增大，冲蚀速率减小，由于弯径比增大时流体流经弯头时运行方向改变减缓，流体对壁面的撞击作用减弱，冲蚀磨损速率降低，因此管道安装时为减小冲蚀磨损可以考虑使用弯径比大的弯头[7]，但考虑到经济性及材料加工问题，推荐使用的弯头弯径比在2～3。

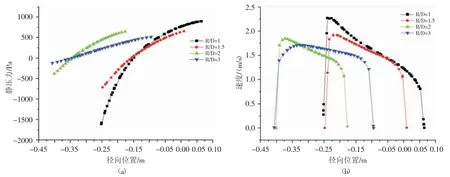
图3 不同弯径比静压与速度曲线对比图

表3 不同弯径比下弯头处最大冲蚀磨损速率

3.2 弯头数量对弯管内流场的影响

建立不同弯头数量的弯管模型模拟分析。从模拟结果可以看出随着弯头数量的增多，多相流体速度先增大后减小（见图4）。两个弯头连接处的立管较短，因此增大的速度会在流经下个弯头时再次被加速，流体速度在第三个弯头处速度、冲蚀磨损速率都增至最大值，由于第四个弯管连接直管段流动方向改变，受二次流的影响流速减小。速度增加时其中夹杂的固体颗粒撞击壁面的能量也增加，冲蚀磨损速率随之增加[8]（见表4，图5）。从图5 看出由于重力的影响水相在弯管外侧分布较多，当输油管道停输或不经常活动管线时管线底部局部死油，而水相会积聚在弯管外侧形成局部积液现象，长期积液会造成管道腐蚀穿孔。

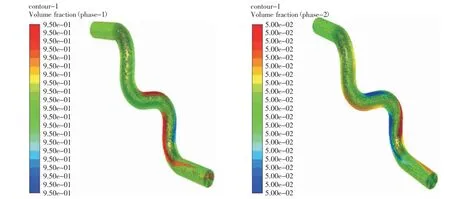
图5 弯管处水油相体积分布图

表4 不同弯头数量下弯头处最大冲蚀磨损速率

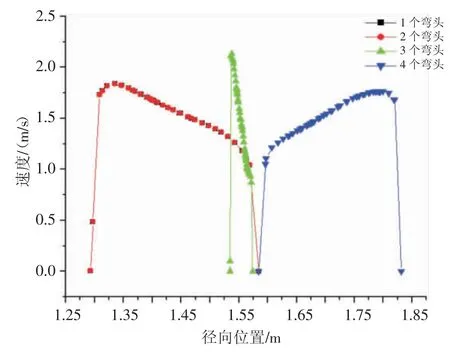
图4 不同弯头数量下速度曲线图

4 结论

（1）通过数值模拟分析表明，多相流体介质流经弯管时在弯头结构的影响下做圆周运动从而产生离心力，由于离心力的作用流体对弯管的外侧壁面施加正向的挤压力，对弯管的内侧壁则产生牵引力，因此沿离心力方向流速减小而压力增加，弯管外侧壁面的冲蚀磨损也最严重。

（2）通过控制变量法比较弯径比、弯头数量对弯管内流场的影响。结果表明：弯径比越小流体流经弯头时速度越大，此时冲蚀磨损速率也最大；随着弯头数量的增多弯管内流速先增大后减小，安装4 个弯头时，第三个弯头处流速最高冲蚀磨损最为严重。

（3）通过数值模拟分析建议管道设计单位在满足现场管道工艺走向的前提下，应尽可能减少流体流动方向的改变，弯头尺寸的选择应优先考虑弯径比在2～3 范围的弯头，并且在管道定期维护与壁厚检测中应增加外侧壁面的检测点，以便及早发现弯头壁厚异常，确保管道输送安全平稳。