用极大交换子群阶的集合刻画Sn①
2022-04-20高丽汪忠碧陈贵云
高丽,汪忠碧,陈贵云
西南大学 数学与统计学院, 重庆 400715
用群的局部性质研究有限群的结构是群结构研究的基本方法. 施武杰最早开始利用群的数量性质来研究有限群的结构, 特别是单群的刻画. 关于交错群和对称群的数量刻画, 文献[1]证明了G≅An当且仅当πe(G)=πe(An), |G|=|An|. 文献[2]证明了G≅Sn当且仅当πe(G)=πe(Sn), |G|=|Sn|, 后来又证明了交错群可以仅用元的阶之集合刻画, 即仅用πe(G)=πe(Sn)刻画. 文献[3]用群的第一ONC-度量刻画了Sn(n≤14). 文献[4]用群的第一ONC-度量和群的阶的最大素因子刻画了Conway单群和Fischer单群. 交换子群的阶和个数是群的重要特征, 文献[5]证明了群G的同阶交换子群的个数之集为{1, 3}等价于群G的同阶子群的个数之集为{1, 3}. 文献[6]仅用极大交换子群的阶刻画了K3-单群. 文献[7-8]仅用极大交换子群的阶刻画了A11、 部分李型单群和散在单群. 文献[9]用极大交换子群的阶刻画了Ap, 其中p和p-2是素数, 即: 全部素图分支数为3的交错群可以用极大交换子群阶的集合刻画.
本文继续探究极大交换子群的阶对群结构的影响, 研究与对称群的极大交换子群阶的集合相同的有限群, 得到Sn(n=5,7,8)可由其极大交换子群阶之集合刻画.
本文所涉及的群都是有限群. 文献[6]用M(G)代表有限群G的全部极大交换子群的阶的集合, 但此符号在不同文献中有不同含义. 本文为了方便, 用πmas(G)代表有限群G的全部极大交换子群的阶的集合, 其余符号都是标准的.
引理1[10]G是有限群且素图不连通, 则下列结论之一成立:
(i)G为Frobenius群;
(ii)G为2-Frobenius群;
(iii)G有正规列: 1◁_H◁_K◁_G, 使得H和G/K是π1-群,K/H是非交换单群,H是幂零群, 其中2∈π1, 且|G/K|||Out(K/H)| .
引理2[11]设G=HK是以K为Frobenius核,H为Frobenius补的Frobenius群, 则K幂零, 且|H||(|K|-1). 特别地, 若p∈π(H)且q∈π(K), 则|Hp||(|Kq|-1), |H||(|Kq|-1). 此时,t(G)=2,Γ(G)={π(H),π(K)}.
引理3[11]设G是2-Frobenius群, 则G=DEF, 其中D和DE是G的正规子群,DE和EF是分别以D和E为核的Frobenius群. 此时,t(G)=2,π1(G)=π(D)∪π(F),π2(G)=π(E).
引理4[12]设G是2a3b5c7d阶单群, 则G同构于下述群之一:
(i)Z2,Z3,Z5,Z7;
(ii)A5,L2(7),A6,L2(8),U3(3),U4(2);
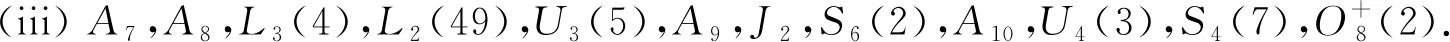
在以下定理的证明中, 若G为Frobenius群或2-Frobenius群, 则默认沿用引理2和引理3的记号, 并不再加任何说明.
定理1设G是有限群, 若πmas(G)=πmas(S5), 则G≅S5.
证由Magma计算知,S5的极大交换子群的阶分别为4,5,6, 则|G|=2n·3·5(n≥2). 由极大交换子群的阶可知G的素图不连通, 且t(G)=2,π1(G)={2, 3},π2(G)={5}. 由引理1, 需讨论如下3种情形:
情形1 若G为Frobenius群, 设G=HK. 由引理2知,π(K)=π1(G)={2, 3},π(H)=π2(G)={5}, |K|=2n·3, |H|=5. 由引理2, 得5=|H||(|K3|-1)=2, 矛盾. 因此,G不能是Frobenius群.
情形2 若G为2-Frobenius群, 设G=DEF. 由引理2知,π(D)∪π(F)={2, 3},π(E)={5}. 此时, |F||(|E|-1), 所以|F||4, 则3∈π(D). 因为D3E是一个以D3为Frobenius核的Frobenius群, 所以|E||(|D3|-1), 而|E|=5, |D3|=3, 矛盾. 因此,G不能是2-Frobenius群.
情形3 若G有正规列1◁_H◁_K◁_G, 使得H和G/K是{2, 3}-群,K/H是非交换单群,H是幂零群, 其中2∈π1, 且|G/K|||Out(K/H)| .
易知, 5∈π(K/H), 且π(K/H)⊆{2, 3, 5},K/H为非交换单群. 若H>1, 则Z(H)>1, 由G的极大交换2-群的阶为4, 知|Z(H)|=2,4. 再由Z(H) charH◁_G, 知Z(H)◁_G. 取P5∈Syl5(G), 由N-C定理知,P5在Z(H)上的共轭作用是平凡的, 则P5Z(H)是G的10阶或20阶交换子群, 矛盾. 因此,H=1. 此时,CG(K)=1, 否则,KCG(K)=K×CG(K),G有5的倍数阶交换子群, 矛盾. 因此A5≅K≤G≤Aut(K), 若|G/K|=1, 则G≅A5, 而A5的极大交换子群的阶与G的阶并不相等, 矛盾. 因此, |G/K|=2,G=S5.
定理2设G是有限群, 如果πmas(G)=πmas(S6), 则G≅S6.
证由Magma计算知πmas(S6)={5, 6, 8, 9}, 所以|G|=2n·3m·5(n≥3,m≥2). 由极大交换子群的阶可知G的素图不连通, 且t(G)=2,π1(G)={2, 3},π2(G)={5}. 于是有如下可能性:
若G为Frobenius群, 设G=HK. 由引理2知,π(K)=π1(G)={2, 3},π(H)=π2(G)={5}, |K|=2n·3m, |H|=5. 再由n≥3,m≥2, 知K有36阶交换子群, 矛盾.
若G为2-Frobenius群, 设G=DEF. 由引理2知π(D)∪π(F)={2, 3},π(E)={5}. 由|F||(|E|-1), 得|F||4, 从而π(F)={2}, 3∈π(D). 取D3∈Syl3(D), 易知D3E是以D3为核的Frobenius群, 由Z(D3) charD3◁_D3E, 得Z(D3)◁_D3E. 已知G的极大交换3-子群的阶为9, 则|Z(D3)|=3,9. 于是,E在Z(D3)上的共轭作用是平凡的, 从而D3E有15阶元,G有15阶交换子群, 矛盾. 因此,G不能是2-Frobenius群.
若G有正规列1◁_H◁_K◁_G, 使得H和G/K是{2, 3}-群,K/H是非交换单群,H是幂零群, 其中2∈π1, 且|G/K|||Out(K/H)| .
易知, 5∈π(K/H), 且π(K/H)⊆{2, 3, 5},K/H是非交换单群. 若|H|>1, 可设|H|=2l·3h(l≤n,h≤m), 由H是幂零群, 可知H=P2P3, 其中P2∈Syl2(H),P3∈Syl3(H),Pi◁_G(i=2,3), 若Pi≠1, 则Z(Pi)≠1, 且Z(Pi) charPi◁_G, 得Z(Pi)◁_G(i=2,3). 由πmas(G)={5, 6, 8, 9}知|Z(Pi)||8或|Z(Pi)||9. 取P5∈Syl5(G), 则P5在Z(P2)和Z(P3)上的共轭作用都是平凡的, 分别产生10阶元和15阶元, 这与πmas(G)={5, 6, 8, 9}矛盾. 因此P2=P3=1, 故H=1. 若CG(K)≠1, 则G有5的倍数阶交换子群, 矛盾. 因此CG(K)= 1. 进而K≤G≤Aut(K),π(K)={2, 3, 5}. 于是K可能是A5,A6, 或者U4(2).
若K≅A5, 则|G/K||2, 则|G|=60,120, 矛盾. 若K≅U4(2), 则K有12阶交换子群, 矛盾. 若K/H≅A6, 即K≅A6, 此时|G/K||4, 则G≅S6,PSO3(9),M10,PΓO3(9). 因为PSO3(9)和PΓO3(9)有10阶交换子群, 所以G≅S6,M10. 若G≅M10, 则6∉πmas(G), 矛盾. 综上所述,G≅S6.
定理3设G是有限群, 若πmas(G)=πmas(S7), 则G≅S7.
证由Magma计算知πmas(S7)={6, 7, 8, 9, 10, 12}, 则|G|=2n·3m·5·7(n≥3,m≥2). 由极大交换子群的阶可知G的素图不连通, 且t(G)=2,π1(G)={2, 3, 5},π2(G)={7}. 于是有如下可能性:
若G为Frobenius群, 设G=HK. 由引理2,π(K)=π1(G)={2, 3, 5},π(H)=π2(G)={7}. 因此, |K|=2n·3m·5, |H|=7. 由|H||(|K5|-1)可得矛盾. 因此,G不是Frobenius群.
若G为2-Frobenius群, 设G=DEF. 由引理2和引理3,π(D)∪π(F)={2, 3, 5},π(E)={7}, |F||(|E|-1). 于是|F||6, 5∈π(D). 同理由|E||(|D5|-1)可得矛盾. 因此,G不是2-Frobenius群.
若G有正规列1◁_H◁_K◁_G, 使得H和G/K是{2, 3, 5}-群,K/H是非交换单群,H是幂零群, 其中2∈π1, 且|G/K|||Out(K/H)| . 易知7∈π(K/H), 且π(K/H)⊆{2, 3, 5, 7}.
设|H|=2l·3h·5(l≤n,h≤m), 由H是幂零群, 可设H=P2P3P5, 其中P2∈Syl2(H),P3∈Syl3(H),P5∈Syl5(H). 根据PicharH◁_G, 得Pi◁_G(i=2,3,5). 若Pi≠1, 则Z(Pi)≠1, 且Z(Pi) charPi◁_G, 得Z(Pi)◁_G(i=2,3,5). 取P7∈Syl7(G), 则P7在Z(P2),Z(P3)和Z(P5)上的共轭作用都是平凡的, 从而G有7的倍数阶交换子群, 矛盾. 因此,P2=P3=P5=1, 从而H=1. 再次由G无7的倍数阶交换子群得CG(K)=1. 从而K◁_G◁_Aut(K).
因为7∈π(K/H),π(K/H)⊆{2, 3, 5, 7}, 由引理4得K同构于下列单群之一:
A7,A8,A9,U3(3),U4(3),L3(2),L2(8),L3(4),S6(2)
若K同构于L3(2),L2(8)或U3(3)之一, 则Aut(K) 无12阶交换子群, 从而G也无12阶交换子群, 矛盾. 因为A8有15阶交换子群, 所以KA8. 另外, 由L3(4),A9,U4(3),S6(2)分别有16,16,81,15阶交换子群知,K不能为L3(4),A9,U4(3),S6(2). 因此K≅A7,A7◁_G◁_S7. 由于A7无12阶交换子群, 所以G≅S7.
定理4设G是有限群, 若πmas(G)=πmas(S8), 则G≅S8.
证由Magma计算知πmas(S8)={7, 8, 10, 12, 15, 16, 18}, 则|G|=2n·3m·5·7(n≥4,m≥2). 由极大交换子群的阶可知G的素图不连通, 且t(G)=2,π1(G)={2, 3, 5},π2(G)={7}. 于是有如下可能性:
若G为Frobenius群, 设G=HK. 由引理2知,π(K)=π1(G)={2, 3, 5},π(H)=π2(G)={7}. 因此, |K|=2n·3m·5, |H|=7. 仿照定理3G为Frobenius群的情形, 由|H||(|K5|-1)可推得矛盾.
若G为2-Frobenius群, 设G=DEF. 由引理2,π(D)∪π(F)={2, 3, 5},π(E)={7}. 同定理3G为2-Frobenius群的情形, |F||6, 于是5∈π(D). 又因为D5E是以D5为核的Frobenius群, 所以|E||(|D5|-1), 但是|E|=7, |D5|=5, 矛盾. 因此G不能为2-Frobenius群.
若G有正规列1◁_H◁_K◁_G, 使得H和G/K是{2, 3, 5}-群,K/H是非交换单群,H是幂零群, 其中2 ∈π1, 且|G/K|||Out(K/H)| . 易知, 7∈π(K/H). 仿照定理3可证H=1, 并且CG(K)≠1 将导致G含有7的倍数阶交换子群, 因此CG(K)=1, 进而K◁_G◁_Aut(K).
因为7∈π(K/H)⊆{2, 3, 5, 7},K/H是非交换单群, 由引理4可知,K/H≅A7,A8,A9,U3(3),U4(3),L3(2),L2(8),L3(4),S6(2).
若K≅A7, 则A7◁_G◁_S7, 但S7无15 阶子群, 故G无15阶子群, 矛盾. 由A9有27阶极大交换子群, 则KA9. 当K为L3(2),L2(8),U3(3) 之一时,G无15阶极大交换子群, 所以K≠L3(2),L2(8),U3(3). 因为U4(3)中有81阶交换子群, 所以K≠U4(3). 又由S6(2)有32阶交换子群知K≠S6(2). 若K=L3(4), 由于G含有15阶交换子群, 而L3(4)却没有, 因此G必定包含L3(4)被3阶群的扩张PGL3(4), 但由Magma计算知PGL3(4)包含21阶元, 矛盾. 综上所述,K≅A8, 从而A8◁_G◁_S8, 易得G≅S8.
