基于多种模型组合的短时交通流预测

王德广, 张轶楠

(大连交通大学, 软件学院，辽宁, 大连 116028)

0 引言

短时交通流预测在改善日益复杂的现代交通方面是极其重要的一环。通过对现有交通数据的分析，预测出各个路段未来短时间内可能产生的交通流量，从而提前掌握交通管控的主动权。一方面，由于短时交通存在时间短、不确定性高的特点，受到的影响因素有很多，比如节假日、天气等；另一方面，每个人生活出行又呈现出固定性，比如日常的上班、上学等，这样短时交通流预测就可以从中找出规律，进行合理预测。

在过去的几十年间，很多从业者及专家学者不断钻研、创新，建立了多种指挥交通的管理系统，与此同时许多数据分析模型也已逐步成熟[1]。例如循环神经网络(Recurrent Neural Network, RNN)等。20世纪90年代，在机器学习的基础上衍生出集成学习的概念：通过构建并结合多个学习器来完成学习任务[2]。

因此，本研究针对短时交通流量预测设计了以长短时记忆神经网络(Long-and Short-Term Memory，LSTM)[3]、门控循环单元(Gated Recurrent Unit，GRU)[4]及栈式自编码器(Stacked Auto Encoder，SAE)，在简单循环单元(Simple Recurrent Units，SRU)模型中进行融合的回归组合预测LGSS模型。

1 回归组合预测模型

1.1 集成学习

在各种机器学习任务中为了追求预测结果准确率更高，可采用组合多个基分类器的方式，这种方式称为集成学习(Ensemble Learning)，如图1所示。

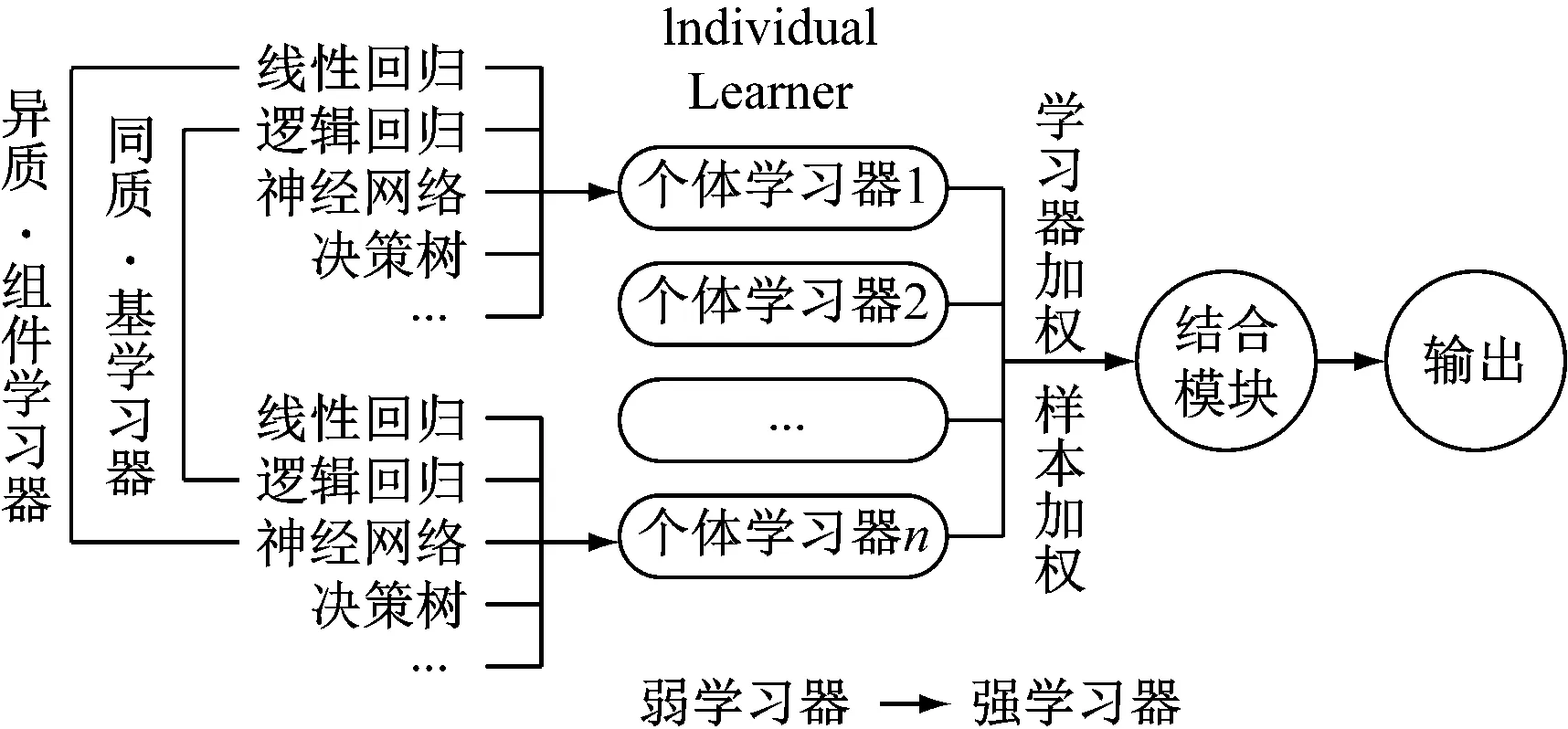
图1 集成学习示意

基分类器通常指的是单一的弱可学习(Weakly Learnable)，分类器使用集成学习的方法，可组合成一个强可学习(Strongly Learnable)分类器[5]。在图1中可以看出强学习器由弱学习器组成的过程。

本研究从回归问题的角度采用集成学习中的Averaging方法进行交通流预测实验。

1.2 LSTM神经网络

LSTM相较于RNN的优势在于利用门限机制，对信息的累计速度进行把控。该模型主要由3个阶段组成，分别为输入门(it)、遗忘门(ft)以及输出门(ot)。这3个门控制可以把控传输状态，保存需要长时间记忆的信息，遗忘不重要的信息。LSTM模型的控制特点使其能够长时间记忆历史数据的状态及自动匹配最佳的时间间隔[6]。

整个存储单元计算过程可以用如下公式表示:

it=σ(wxixt+whiht-1+wcict-1+bi)

(1)

ot=σ(wxoxt+wh0ht-1+wcoct-1+b0)

(2)

ft=σ(wxfxt+whfht-1+wcfct-1+bf)

(3)

ct=ft⊙ct-1+it⊙tanh(wxcxt+wkcht-1+bc)

(4)

ht=ot⊙tanh(ct)

(5)

式中,LSTM模型在t时刻的所有输出定义为ht，σ()及tanh()为激活函数，w和b表示权重系数矩阵和偏置，σ和tanh分别代表Sigmoid和双曲线正切函数。

1.3 GRU神经网络

GRU与LSTM类似，针对门控制进一步优化。在结构和计算上更加简单，只存在更新门和重置门，同时能够保证避免梯度消失以及爆炸的出现[7]，如

zt=σ(wz·[ht-1,xt])

(6)

rt=σ(wr·[ht-1,xt])

(7)

(8)

首先将xt与ht-1拼接进行线性变换，使用Sigmoid激活，计算得出更新门(zt)和重置门(rt)的门值，通过重置门门值作用在ht-1上，就可以得到上一时间所传来信息可利用的数量。接着将重置后的ht-1代入基础的RNN算法中进行计算，得到新的ht。最后不同时间的更新门的门值会作用在相对应的ht上，计算得到的ht之和，从而确定隐含状态输出的ht。

1.4 SAE神经网络

SAE模型作为深度神经网络模型，是由多层稀疏自编码器组成的[8]。

SAE属于非监督学习算法，使用它进行计算操作时必须同时满足以下2种约束。

(1)autoencoder(输入等于输出)：

hw,b(x)≈x

(9)

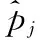
(10)

1.5 SRU神经网络

SRU是依据循环神经网络(RNN)演化而来的深度学习模型。与LSTM 和GRU拥有类似的结构，SRU也是基于“门控”结构构建[9]。

在图2所示的单层SRU中轻度循环(Light Recurrence)和高度网络(High Network)是2部分创新。

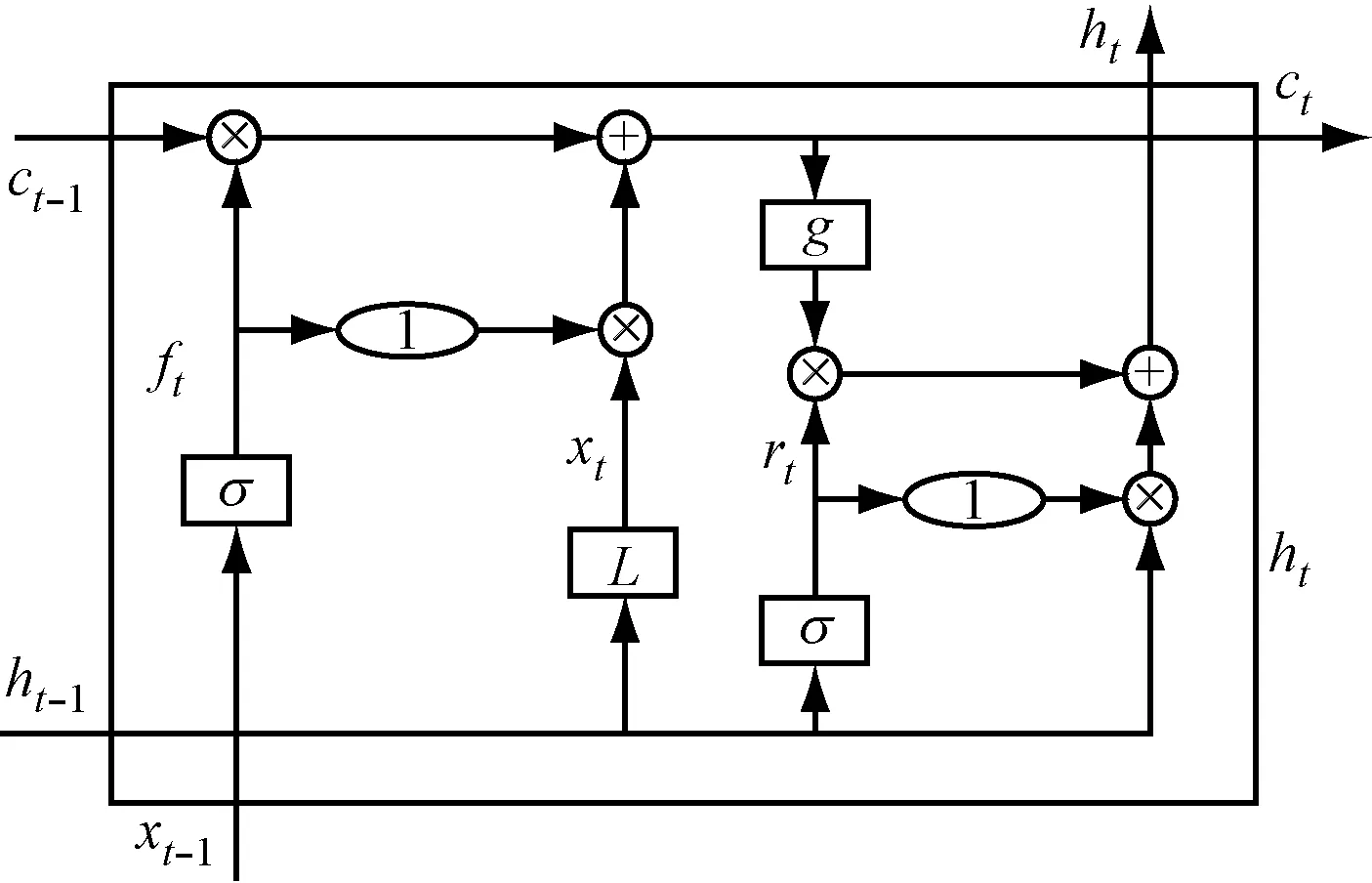
图2 SRU 神经网络结构图

SRU第一个重要部分通过“高度网络”读取输入数据信号xt并计算细胞状态ct的序列，从而获取序列信息。其中Wf、W、bf是需要进行训练得出的参数矩阵，ft是遗忘门。

SRU第二个重要部分是高度网络，又被称为跳跃连接，重置门rt用于组合数据信号xt以及当前细胞状态ct，跳跃连接式为

rt=σ(Wtxt+br)

(11)

ht=rt×g(ct)+(1-rt)×xt

(12)

其中，Wt和br为神经网络训练得出的参数矩阵，(1-rt)×xt称为跳跃式传递，也可称为残差连接。

1.6 评价指标

在交通流预测领域，主要通过以下指标来评价模型的预测准确性[10]。

(1)绝对平均误差(MAE)

(13)

(2)平均绝对百分比误差(MAPE)

(14)

(3)根均方误差(RMSE)

(15)

(4)均方误差(MSE)

(16)

(5)决定系数(R2)

(17)

将所获数据中的实际值(xi)以及对应时间的预测值(yi)代入式中，得到最终的预测精准度。

为了充分比较本研究使用的LGSS组合模型与3种单一模型的预测精准度，采用上述5种评价指标多角度分析。

2 LGSS模型

在处理许多机器学习问题中，将多种预测值取平均，能得到更为准确的结果。因此，采取对多个结果取平均值的方法建立LGSS模型，如图3所示。

图3 LGSS模型示意图

在 Pycharm中导入Keras模块，将训练集时间序列数据以CSV格式存储，用np.array()方法将数据提取，分别放入LSTM、GRU和SAE 3种单一模型中，并设置R2、RMSE、MAPE、MSE、和 MAE函数对模型预测的精准度进行评估，反复进行实验、调整参数，最终训练后在3种神经网络模型中得到各自预测的结果以及精准度。

接下来是LGSS模型中最重要的部分，将3种单一模型预测的结果放入SRU模型中进行融合，取3种单一模型预测结果值的平均值。数据导入步骤与前3种单一模型相同，接着导入封装好的 SRU 程序。在RNN 模型众多同类变形中，计算的先后顺序不同会直接影响结果值，前一期细胞状态的数值大小决定后一期遗忘门和细胞状态的数值大小。因此，必须等到前期计算全部结果完成后，后期计算才可以开始。以下是SRU的计算式：

(18)

ft=σ(wfxt+bf)

(19)

ct=ft×ct-1+(1-ft)×Wxt

(20)

式(14)和式(15)中并没有t-1的滞后项存在，这是SRU模型的最大特点，它采用逐点乘积的计算方式，可以在多个维度和不同步骤中实现并行计算，因此SRU模型相较于其他模型进行相同数据量计算操作时，所用计算时间更少。用Sequential函数将整个神经网络进行初始化，设置隐含层单元数量为32，输入向量长度为6，输出是1。SRU具有高度网络的特点，神经网络中使用了残差连接，相当于为每一个损失函数对当前细胞状态的偏导数提供一个恒等项1，导数值df/dh很小，此方法依旧可以保证误差反向传播的有效性，因此高度网络能够有效防止梯度消失。最后依旧使用R2、RMSE、MAPE、MSE、和MAE函数进行计算和度量，最终输出LGSS组合模型的拟合效果值。

此算法模型的资源消耗主要集中在3种基本模型对各个时间段的交通流数据进行训练:时间复杂度是O(1+n2+n)，根据推导大O阶的方法，时间复杂度确定为O(n2)；在SRU模型计算的时间复杂度为O(n)，最终LGSS模型的时间复杂度为O(n2)。

3 实验

实验环境：Windows 7

开发工具：PyCharm、Tensorflow

3.1 数据集

采用PeMS系统(Performance Measurement System)中的数据进行分析预测，该系统由美国加州交通运输部提供，其数据集在交通流的预测研究中使用最广泛。此数据集中选取多个路段，每5 min对各个路段的交通流数据进行采集。选取2016年1月到4月共12 098条数据，按照约4∶1的比例划分训练集与测试集。

3.2 组合算法分析与结果比较

(1)首先，使用 LSTM、GRU、SAE等3种单一模型对数据进行计算、训练和结果预测，见表1、图4。

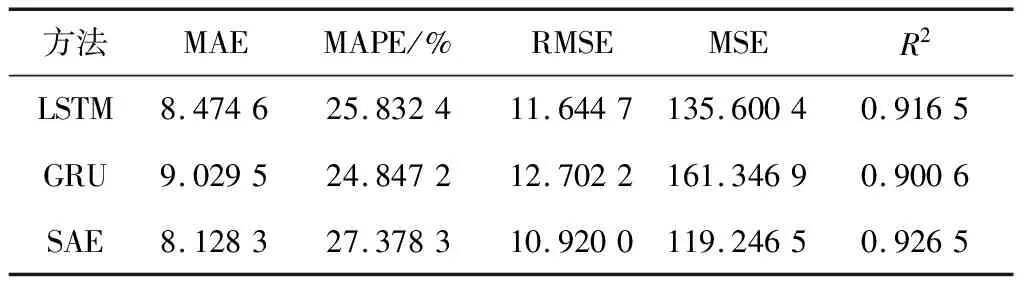
表1 LSTM/GRU/SAE预测结果误差比较

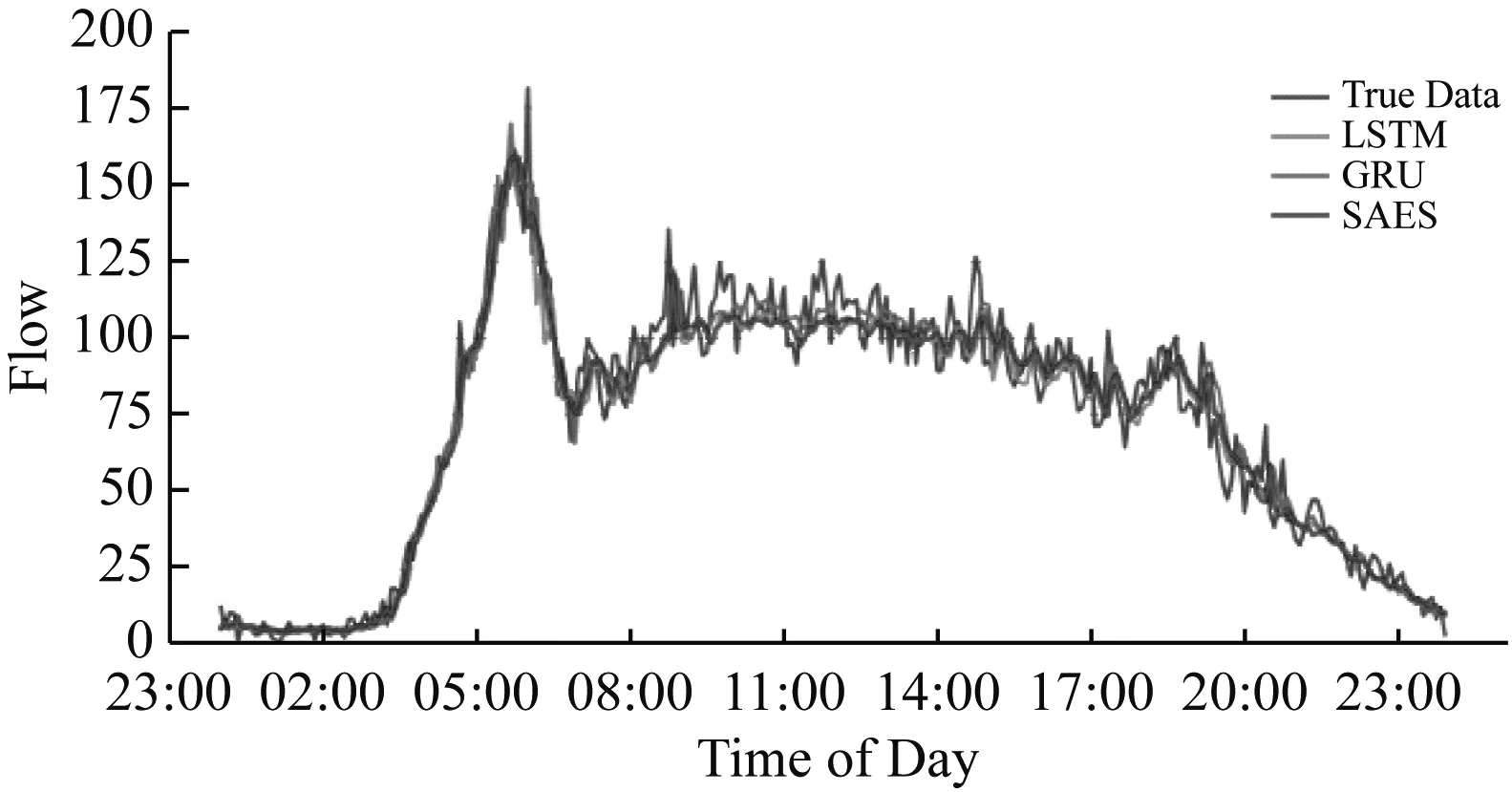
图4 3种单一模型与真实值比较曲线图

(2)将LSTM、GRU、SAE等3种单一模型得到的预测结果值放入SRU单层模型中，最后获取LGSS组合模型的预测精准度：MAE为7.894 6，MAPE为25.004 7%，RMSE为10.550 6，MSE为111.316 2，R2为0.931 5。

从以上5个指标可以看出，LGSS模型相较其他3种单一模型预测精准度更高，如图5所示。

图5 单层SRU模型与真实值比较曲线图

(3)在单层SRU的基础上进行多次迭代，结果见表2。

从表2可以看出，当LGSS模型中SRU进行4次迭代时预测精准度最高、误差最小，如图6所示，但是迭代次数超过5次后，精准度下降、误差变大。

图6 SRU多次迭代时LGSS模型与真实值比较曲线图

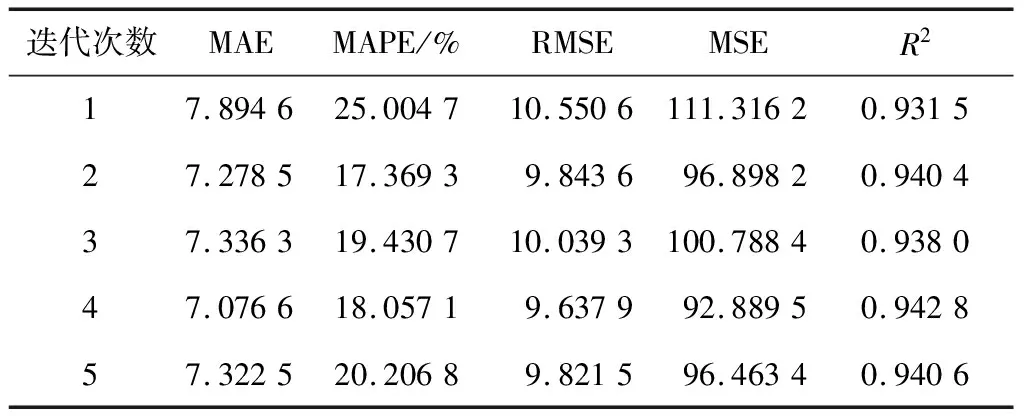
表2 SRU多次迭代时LGSS预测结果值

用本研究其中3个评价指标与文献[11]和文献[12]所做的短时交通流预测实验结果对比见表3。

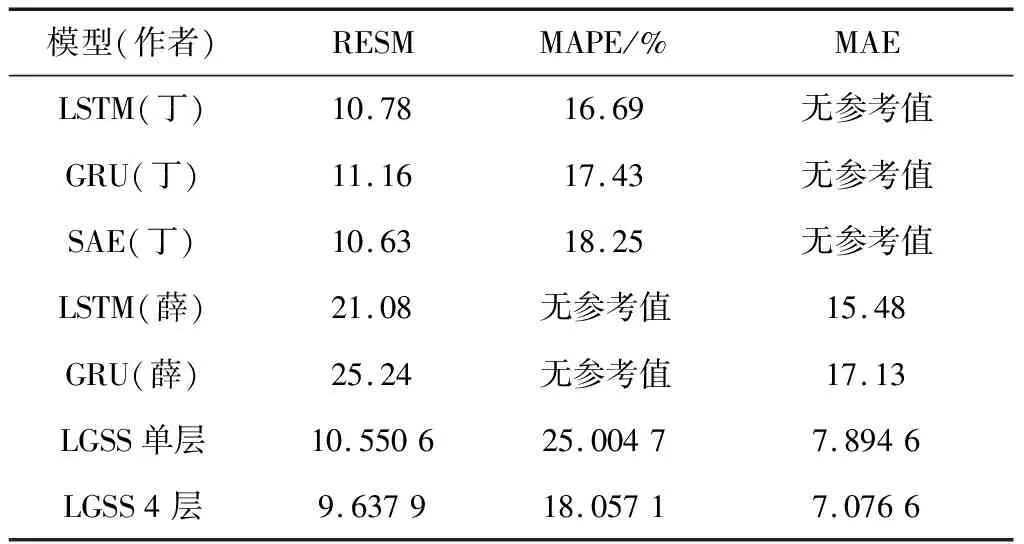
表3 与其他作者实验结果对比

从表3中结果对比可以看出，本论文所进行的一系列实验结果效果优于其他作者的实验结果，LGSS模型中SRU为单层时，预测精准度已经优于其他单一模型，在SRU经过4次迭代后精准度已经有明显提升。

(4)SRU模型具有的高度网络和轻循环结构特点使其可进行并行运算，使其在计算速度上优胜于其他模型。在同为2次迭代时，将LSTM与LGSS组合模型(此时为单层SRU)分别运行10次，取10次运行时间的平均值，在LSTM模型下每次运行时间为1.056 4 s，组合模型运行的模型为0.530 6 s。在保证精度的前提下，组合模型(此时SRU为4次迭代)每次运行时间为0.749 1 s。通过比较单一模型与组合模型的计算时间，可以看出，由于SRU的存在，组合模型比单一模型计算时间缩短很多。

4 总结

LGSS模型样本数据采集时间间隔为5 min一次，平均反映时长0.75 s，MAE值可控制在7.8%以下。当采集时间间隔更短时，LGSS模型计算所需时间略长于采集时间间隔为5 min的计算时间。由于在日常生活中节假日占比较少、极其恶劣天气发生概率较低，其产生的影响不大，所以为了保持LGSS模型的适用性，在数据清洗阶段将节假日期间的数据删除，并排除了天气影响的因素。如果需要研究节假日及特殊时间的短时交通流预测，将指定数据放入LGSS模型计算即可。

由于现代交通相较于传统交通更加复杂，交通流不确定性很高，同时具有高度非线性的特点，单一模型进行短时交通流预测时往往精准度不高。本论文采用集成学习的Averaging方法，将LSTM、GRU、SAE等3种单一模型与SRU模型进行融合组成LGSS模型，将3种单一模型的预测结果取平均值。实验结果表明，组合后的模型较单一模型能有效地避免数据过度拟合，提升了预测的精准度，减小了误差。