不同剪跨比的无腹筋UHPC梁抗剪承载力有限元分析
2022-04-20孔杰威郑小红
孔杰威, 郑小红
(华南理工大学土木与交通学院,广州 510640)
0 引言
近年来,超高性能混凝土(Ultra-High Perfor⁃mance Concrete,简称UHPC)由于其超高强度、超韧性、极好的耐久性等优势在桥梁工程领域备受关注。研究表明UHPC中的钢纤维在混凝土开裂时具有“桥接”的效应,抗拔出的阻力具有抗剪作用,因此,UHPC梁中可以少配甚至配箍筋就能满足抗剪要求[1,2]。
国外,Voo[3,4]对 8 根无腹筋预应力工字型 UHPC梁进行了抗剪试验研究的基础上采用塑性上限模型法对抗剪承载力进行预测比较,计算值和试验值吻合较好,但该模型基于深梁建立的,对于常规尺寸的UHPC梁的适用性还有待考究。Aziz等[5]对9根无腹筋UHPC矩形梁、3根无腹筋HSC梁、3根无腹筋NSC梁进行了抗剪试验研究,分析了混凝土抗压强度、剪跨比和梁高对无腹筋梁抗剪性能的影响,结果表明混凝土抗压强度和剪跨比对抗剪承载力影响较大。
国内,金凌志[6]对无腹筋UHPC简支梁进行了抗剪试验研究,试验结果显示,随着剪跨比的增大,UH⁃PC梁的斜裂缝倾角不断减小。在试验数据的基础上还推算了高强钢筋UHPC梁的抗剪承载力计算式,此公式将UHPC的软化效应、纵筋销栓作用以及UHPC抗拉能力纳入到公式的考虑范围,在桁架-拱模型的基础上做了进一步的拓展与延伸。
从上述研究可以看出剪跨比是无腹筋UHPC梁抗剪承载力的主要影响因素,为了更深入地研究剪跨比对无腹筋UHPC梁抗剪承载力影响,文中通过有限元分析,以剪跨比为主要参数,对无腹筋UHPC梁抗剪承载力进行详细探讨。
1 试验梁设计
为探究剪跨比对无腹筋UHPC梁的抗剪承载力的影响规律,文中以剪跨比λ为参数设计了3组共6根无腹筋UHPC梁,进行抗剪试验。试验梁的截面尺寸为170mm×270mm,长 度 l=2200mm,计 算 跨 径 l0=2000mm。试验梁的受拉/受压纵筋配筋为6C25/2C25,为了使试件发生斜截面抗剪破坏,纵筋配筋率取为8.15%。UHPC钢纤维含量取2%。
设计分组如下表1所示,试验梁详细配筋构造及尺寸如图1所示。
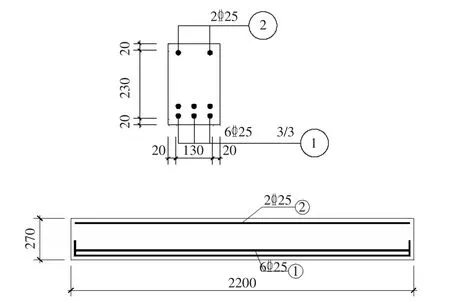
图1 无腹筋UHPC试验梁配筋(单位:mm)

表1 试件梁设计
2 有限元模型
采用有限元ABAQUS软件建立试验梁的有限元分析模型。
2.1 材料本构
2.1.1 钢筋本构
参考文献[7],模型中所有的钢筋本构关系采用如图2所示的钢筋本构模型,钢筋应力在线弹性段(0≤ε≤εy)采用σ=Esε,当钢筋应力达到屈服强度fy时采用强化模型σ=fy+Eu(ε-εy)。钢筋的材料参数如表2所示。

表2 钢筋材料参数
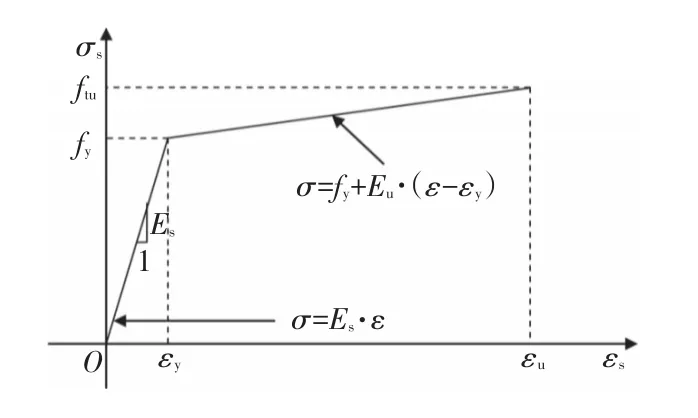
图2 钢筋本构模型
2.1.2 UHPC本构
文中将采用混凝土损伤塑性模型(CDP模型)对UHPC材料进行本构定义。
UHPC单轴受压应力-应变曲线采用杨剑等[8,9]拟合的曲线方程,如式(1)所示。其中ε0=3500με,ξ=ε/ε0,n=Ec/Es,Ec、Es是分别是初始弹性模量和峰值割线模量,根据DBJ 43/T325-2017《活性粉末混凝土结构技术规程》[10]表3.4,Ec取40000MPa。fc取90MPa。
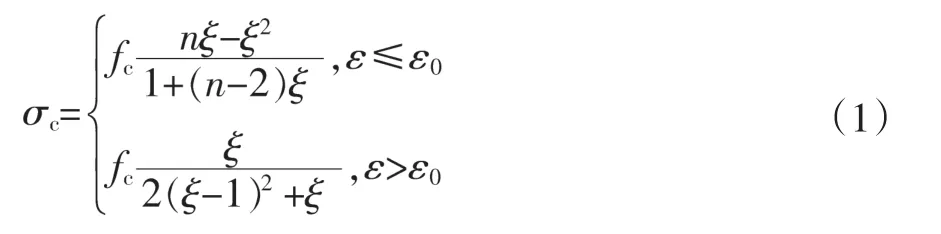
UHPC受拉应力应变曲线分为应变硬化阶段和应力软化阶段[11],在UHPC极限拉应变前用双线性曲线拟合如式(2),其中fct是硬化阶段平均应力,计算中取5MPa;应变软化段采用式(3)的应力-裂缝宽度函数,根据法国规范AFGC2013,混凝土应变和裂缝开展的关系如式(4)所示,LR是建议长度,LR=2/3h,h为梁截面高度。
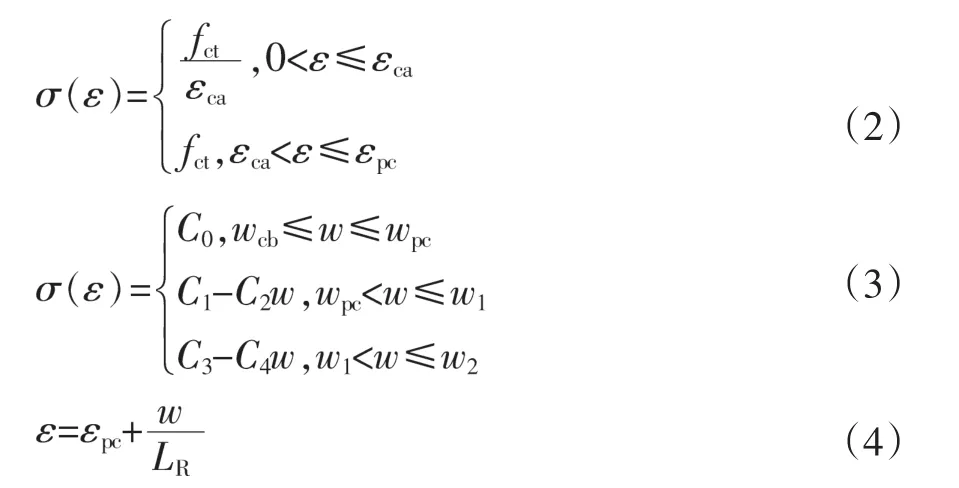
参考普通混凝土损伤因子的确定方法,目前主要有能量损失法[12]和比例应变法[13]对损伤因子进行计算,文中将采用比例应变法中的计算式(5)、式(6)对UHPC的损伤因子进行计算确定。
UHPC受压时:
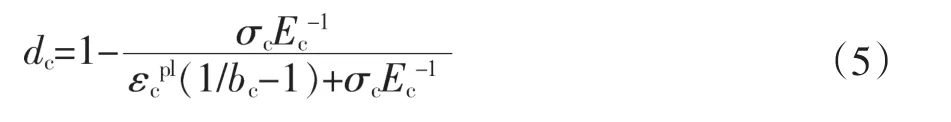
式中,dc为UHPC压缩损伤因子;Ec为UHPC的初始弹性模量;σc为UHPC的抗压强度;εtpl为UHPC的压缩塑性应变;bc为常量,0<bc≤1。
UHPC受拉时:
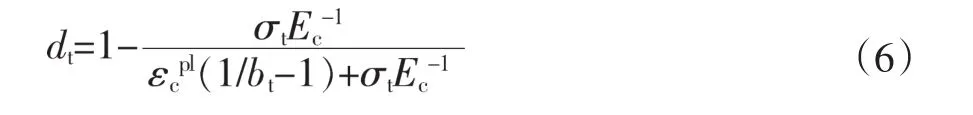
式中,dt为UHPC拉伸损伤因子;Ec为UHPC的初始弹性模量;σt为UHPC的抗拉强度;εtpl为UHPC的拉伸塑性应变;bt为常量,0<bt≤1。
参考文献[14],文中有限元分析过程中采用的UHPC塑性参数如表3所示,其中μ为粘性系数,合适的粘性系数可以使计算收敛得更快。

表3 UHPC塑性参数
2.2 单元选取与边界条件
采用有限元ABAQUS软件建立和试件梁条件相同的分析模型,图3为建立的试验梁有限元几何模型。UHPC梁体使用实体单元(C3D8R)模拟,网格尺寸采用25mm,钢筋使用桁架单元(T3D2)模拟,网格尺寸采用50mm。
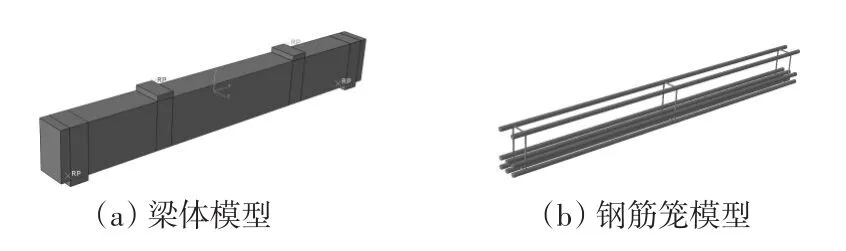
图3 有限元几何模型
有限元模型中的边界条件设置和试验中的边界条件保持一致,即两端铰接。在支座和加载头位置建立钢垫片模型,钢垫片与UHPC梁体间建立粘结(Tie)的相互关系。将支座垫片的底面和加载垫片的顶面自由度分别耦合(Coupling)到参考点上,对支座钢垫片参考点施加简支约束,在加载钢垫片参考点处施加一y轴负方向的位移,位移根据定义表格幅值的形式进行线性加载,施加30mm的位移于加载点处。
3 计算结果分析
3.1 有限元模型的验证
对试验梁VD-1~VD-3(即剪跨比为1.4、2.4、3.2的情况)进行无腹筋UHPC梁的抗剪性能试验研究。将有限元结果和试验结果进行对比,极限荷载值如表4所示,对比曲线如图4所示,破坏形态对比如图5所示。
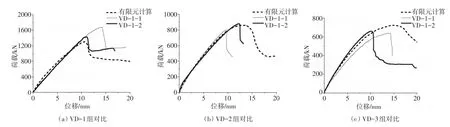
图4 荷载-位移曲线对比
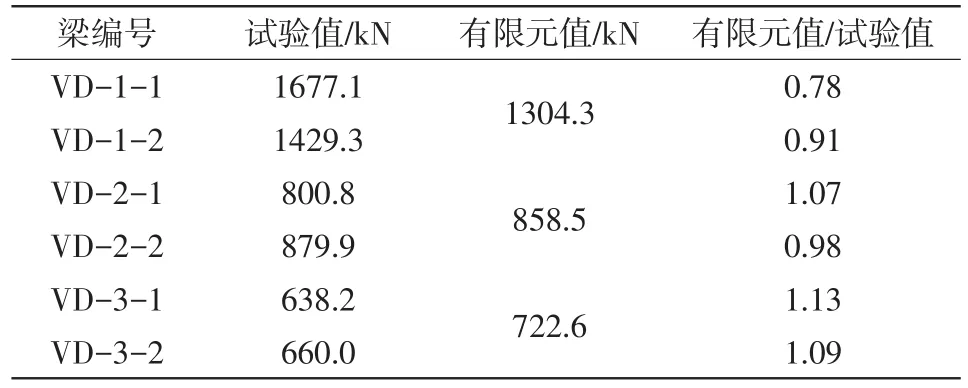
表4 有限元与试验极限荷载比较
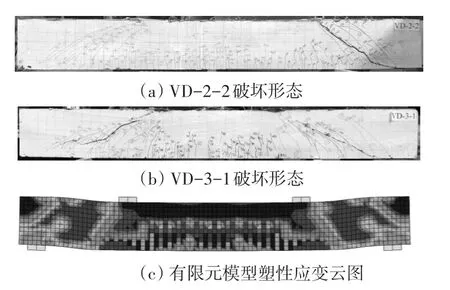
图5 梁破坏形态对比
从表4和图4分析可得,除试验梁VD-1-1承载力偏高外,其他试件的有限元数值模拟对极限承载力的计算较为准确,文中的有限元分析方法能很好预测试验梁的极限荷载,有限元模拟的梁刚度和试验梁刚度上升段非常接近。如图5所示,试验梁VD-1和VD-2的破坏形态为剪压破坏,VD-3为斜拉破坏,有限元模型梁的混凝土塑性应变云图基本可以还原试验梁的破坏形态,若要获得更好的效果,可进一步细化网格尺寸。以上对比结果说明CDP模型对UHPC的模拟具有良好的适用性。
但是荷载-位移曲线下降段的有限元计算值和试验值有一定差别,试验中UHPC梁达到极限承载力后,荷载-位移试验曲线均是突然竖直下降,这是因为UHPC是一种纤维和混凝土的复合材料,试验中斜截面的钢纤维全部拔出后,截面突然失去了抗剪能力,破坏具有一定的脆性;而有限元模拟中,UHPC的破坏是通过定义本构曲线的软化段来考虑的,与钢纤维逐渐拔出、截面突然失效的实际破坏情况有区别。
3.2 剪跨比的影响规律
为详细探究剪跨比的影响规律,因此把有限元分析在试验梁的基础上增设剪跨比为1.0、1.9、2.8、3.6的模型梁。
如图6和表5所示,随着剪跨比的增大,荷载-位移曲线上升段的刚度逐渐减小,试验梁的承载力峰值位置后移,且极限承载力不断减小,与剪跨比为1.0的模型梁相比,其余模型梁极限承载力分别减小了28.2%、44.0%、52.7%、57.2%、60.2%、63.3%。这是因为剪跨比越大,在相同荷载作用下,梁弯剪段斜截面弯矩越大,因此梁的斜裂缝开展越早,斜截面剪切破坏更快,但随着剪跨比的增大,无腹筋UHPC梁的承载力降低速率逐渐减小。
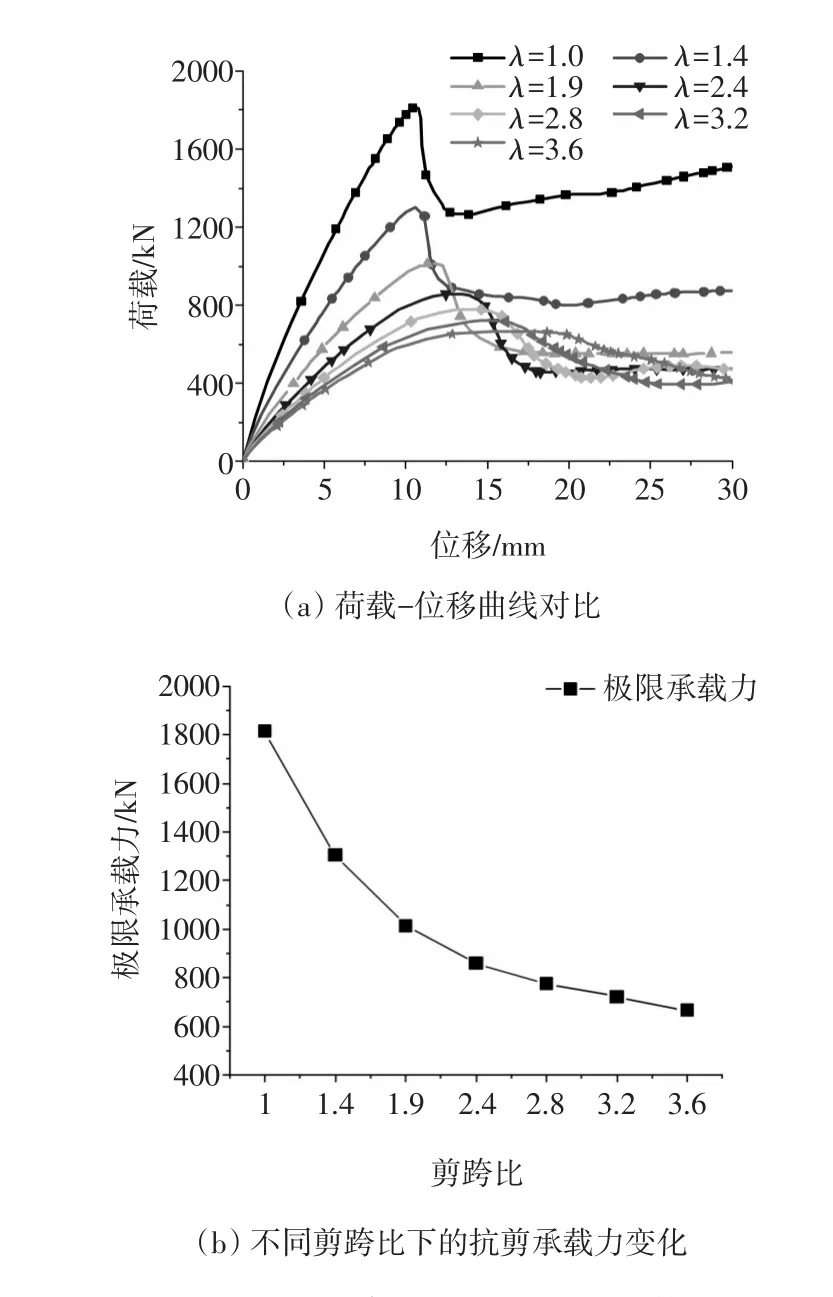
图6 不同剪跨比下的有限元分析结果
3.3 不同剪跨比下的不同配筋率的影响规律
为进一步研究剪跨比的影响规律,在不同剪跨比下(1.4、2.4、3.2)增设了不同配筋率(5.44%、6.64%、9.85%、11.25%)的情况。
计算结果如图7和表6所示,由图表可知,在不同剪跨比下,试验梁的极限承载力均随着配筋率的提高而提高。随着剪跨比的增大,纵筋配筋率对极限承载力的提高幅度越来越小,这是因为随着剪跨比的增大,纵筋的销栓作用越来越小,因此配筋率对极限承载力的影响也越来越小,在不同剪跨比下,纵筋配筋率对无腹筋UHPC梁的抗剪承载力的影响不同,剪跨比和纵筋配筋率对抗剪承载力的影响存在一定的耦合现象。
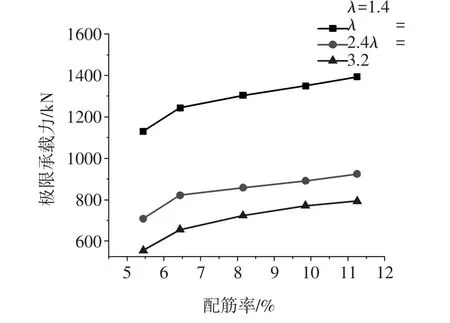
图7 不同剪跨比、配筋率下梁的抗剪承载力
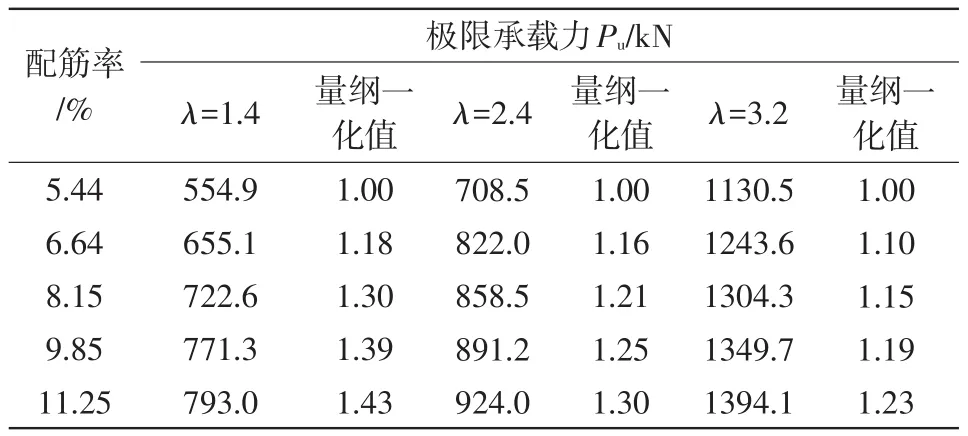
表6 不同剪跨比、配筋率下的极限荷载
4 结语
通过有限元分析结果,可以得出以下结论:
(1) 除试验梁VD-1-1承载力偏高外,其他试件的有限元数值模拟对极限承载力的计算较为准确,文中的有限元分析方法能很好预测试验梁的极限荷载,有限元模拟的梁刚度和试验梁刚度上升段非常接近,说明CDP模型对UHPC的模拟有良好的适用性。
(2) 随着剪跨比的增大,极限承载力不断减小,与剪跨比为1.0的模型梁相比,其余模型梁极限承载力分别减小了28.2%、44.0%、52.7%、57.2%、60.2%、63.3%。随着剪跨比的增大,无腹筋UHPC梁的承载力降低速率逐渐减小。
(3) 在不同剪跨比下,纵筋配筋率对无腹筋UHPC梁的抗剪承载力的影响不同。随着剪跨比的增大,纵筋配筋率对极限承载力的提高幅度越来越小。剪跨比和纵筋配筋率对抗剪承载力的影响存在一定的耦合现象。
