基于GMF方法的捕风一号风速反演分析

2022-04-20范东栋卢敏健陈趁新高涵尉昊赟

中国空间科学技术 2022年2期

关键词：反演镜面风速

范东栋，卢敏健，陈趁新，高涵，尉昊赟,*

1. 航天东方红卫星有限公司，北京 100094

2. 清华大学精密仪器系，北京 100084

1 引言

海面风是海洋各种运动的主要动力来源，是形成海面波浪的直接动力，维持着区域与全球气候；同时海面风也是气象预报的必要参数，直接影响海上航行、海洋工程、海洋渔业等。

传统的海面风探测手段，如海洋浮标、船舶、海洋站等，存在观测点少、观测区域受限、难以实现大范围和恶劣天气条件下的实时有效观测等问题。为此，基于微波散射计[1]、激光测风雷达[2]、全球导航卫星系统-反射测量(global navigation satellite system-reflectometry，GNSS-R)[3]等技术的星载海面风探测技术得到了广泛关注。其中，GNSS-R技术直接利用卫星导航系统全球覆盖的微波信号源，具备全天时全天候观测、星载设备体积小成本低等优势，发展前景良好，应用潜力巨大[4]。2000年，Zavorotny和Voronovich基于双基雷达方程[3]，提出了二维时延-多普勒模型。进一步，研究者结合不同海面反射条件下GNSS-R波形不同的特点，利用波形的不同特征，如平均功率、前沿斜率、后沿斜率等，构建波形特征参量与风速的回归模型，实现风速反演。2003年，UK-DMC卫星进行了首次星载GNSS-R探测试验，验证了在轨海面风探测应用的可行性[5-6]。之后，国外相继启动了多个星载GNSS-R计划，其中最为著名的是2016年 NASA发射的用于热带气旋监测的低轨卫星星座——飓风卫星导航系统(cyclone global navigation satellite system，CYGNSS)[7]。CYGNSS的发射，极大地推动了GNSS-R风速反演技术的发展，C. Ruf 等人基于归一化双基雷达散射截面(normalized bistatic radar cross-section，NBRCS)和前沿斜率两个特征量，分别构建了经验性地球物理模型函数(geophysical model functions，GMF)，并通过高低风速不同建模及反演风速最小方差融合等方法，实现了风速反演性能的提升并向高风速段迈进。特别值得一提的是，对飓风核心处的风速反演结果与NOAA P-3机载测量数据具有较好的一致性[8-9]。近年来，随着人工智能和深度学习技术的发展，新型反演算法也得到了快速发展。在各级算法发展的大力支持下，CYGNSS星座持续提供L1数据及风速反演L2、L3数据[8-9]，并将反演数据产品延拓到土壤湿度[10]等。在CYGNSS取得一系列成果和国内GNSS-R技术走向成熟[11-13]的共同推动下，2019年6月5日，中国成功发射捕风一号A/B 卫星，开展GNSS-R技术在轨试验。

本文基于GMF方法，实现了中国首颗GNSS-R卫星捕风一号数据的风速反演及初步性能评估，可为后续卫星星座设计提供参考。

2 风速反演原理

捕风一号卫星接收机与CYGNSS接收机类似，在轨接收到的前向散射信号主要来自导航卫星、地表、探测卫星三者在满足以地表为“镜面”的镜面反射几何条件下的反射信号，如图1所示。其中，T、R分别为GNSS卫星和GNSS-R卫星；XYZ、XTYTZT、XRYRZR分别为地心惯性坐标系、GNSS卫星本体坐标系和GNSS-R卫星本体坐标系。S为镜面反射点，以S为原点，建立镜面反射点本体坐标系，其中Z0轴指向镜面反射点法线方向，Y0轴位于OTR平面内，X0轴垂直上述平面。此外，VT，VR分别为GNSS卫星和GNSS-R卫星的速度矢量；Re、HT、HR分别为地球半径、GNSS卫星高度和GNSS-R卫星高度；RT、RR分别为GNSS卫星和GNSS-R卫星到镜面点的距离；θ为镜面点入射角。

图1 GNSS-R观测几何示意Fig.1 Geometry of GNSS-R measurement

根据Zavorotny和Voronovich模型(ZV模型[3])，导航卫星、镜面点、探测卫星三者位置与速度关系在镜面点附近形成椭圆环带的等延迟面(等传输路径长度)和呈曲线状分布的等多普勒条带(等相对运动速度)。按相应时延-多普勒二维分割得相关功率信号，形成延迟-多普勒映射图(delay-Doppler mapping，DDM)。每一DDM单元对应的相关功率可表示为：

(1)

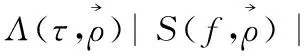
进一步考查式(1)中NBRCS (即σ0)项，图2给出了按照捕风卫星在轨参数及镜面点入射角20°条件仿真得到的σ0分布情况。可以看出在风速1 m/s时，以镜面点为中心20 km×20 km仿真区域内的σ0为曲面分布，此时洋面与海面风场之间的耦合也较弱；而在风速2 m/s时，σ0趋于一个恒定值。更高风速的仿真同样表明，σ0在镜面点区域附近保持恒定。因此，GNSS-R分析建模中，可将式(1)中σ0项在整个镜面点附近区域视作单一取值置于积分项外，这样，通过对公式中其他参数的定标及校准计算即可由观测量导出与洋面风速直接相关的镜面点区域σ0。图3给出了仿真得到的不同镜面点入射角时，NBRCS与风速的对应关系，可以看到，在给定镜面点入射角的情况下，两者呈一一对应关系。正是基于这一内在关联，可通过建立NBRCS和风速的回归GMF模型，实现风速反演。

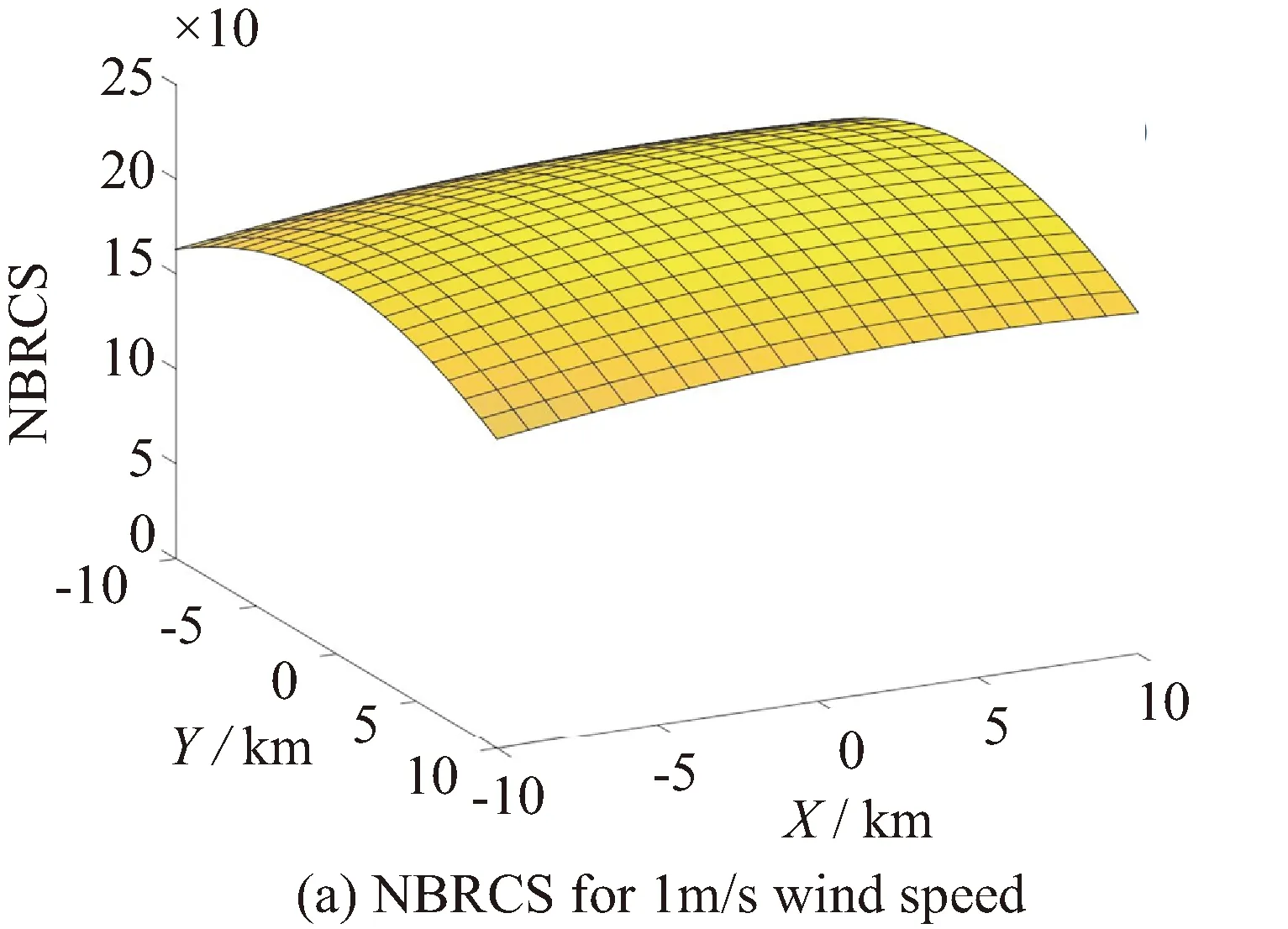
图2 不同风速下NBRCS仿真Fig.2 Simulation of NBRCS with different wind speed

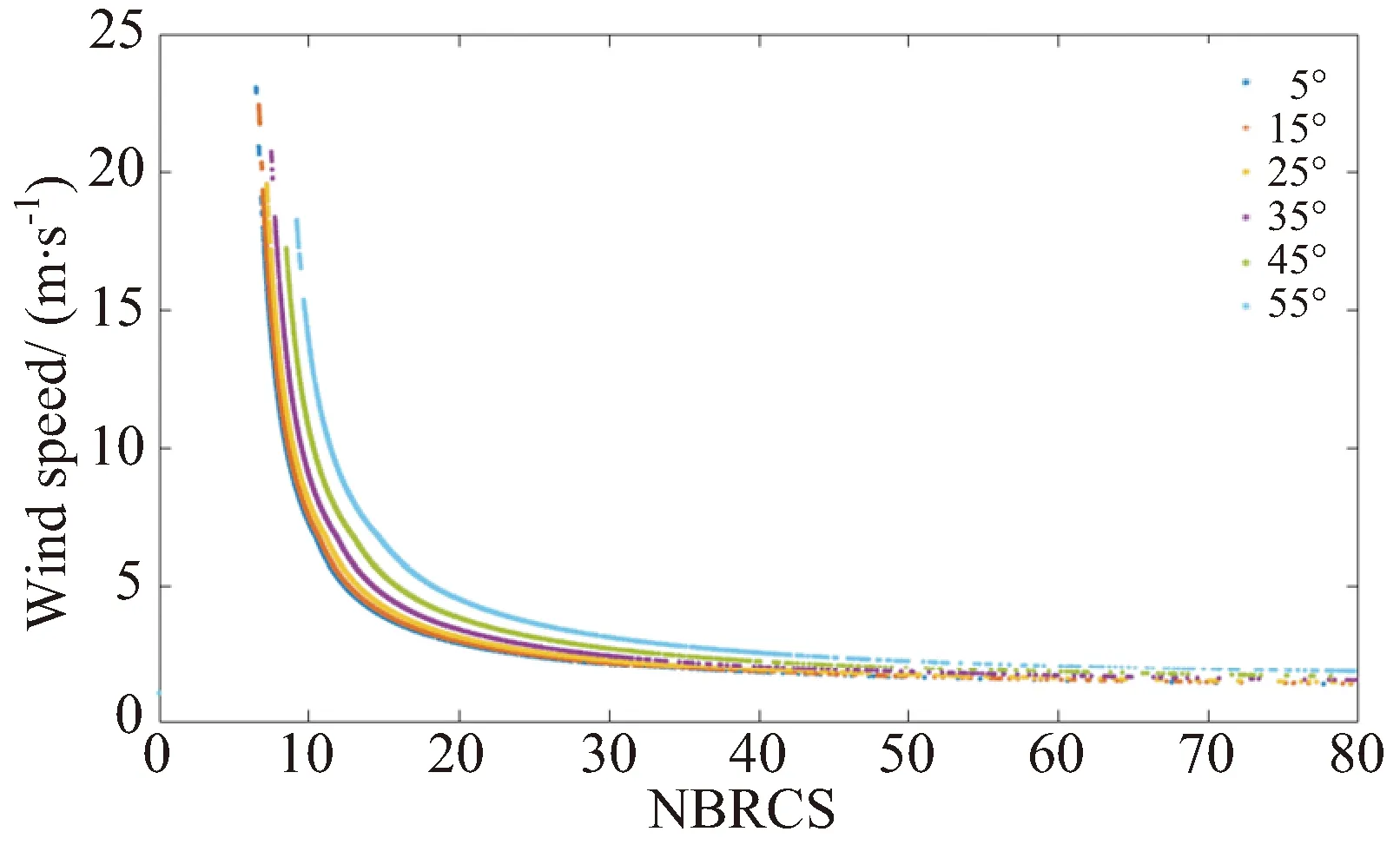
图3 不同入射角时NBRCS与风速关系仿真结果Fig.3 Simulated relationship between NBRCS and wind speed for different incident angles

3 风速反演流程与建模

3.1 反演分析流程

为了便于反演性能的验证评估，本文采用CYGNSS风速反演的同一算法，该风速反演算法以文献[14]为基础，利用在轨观测数据和约定风速参考构建经验性参数化GMF回归方程，实现风速反演。图4给出了风速反演的基本流程。其中地理数据用于筛选出洋面数据，以全球陆地1 km级基准海拔数据(global land one-kilometer base elevation，GLOBE[15])为基础，并将陆面区域延拓15 km以避免近岸效应的影响。参考风速集选用欧洲中期天气预报中心(European center for medium-range weather forecasts，ECMWF)ERA-Interim[16]小时级再分析海面风速数据。通过将ERA-Interim再分析数据的空间位置二维线性差值和时间一维线性差值与观测数据进行时空匹配，并将匹配后的风速作为建模的参考风速。

图4 风速反演流程Fig.4 Flow chart for wind speed retrieval

3.2 反演输入观测数据集

捕风一号试验卫星1级数据包含15个数据变量：观测时间参数(week，second，time_utc)；观测时刻捕风卫星位置速度参数(remote_ecef)；导航卫星类型、PRN和位置速度(gnss_type，gnss_prn，gnss_ecef)；镜面点位置速度和反射信号角度(reflect_ecef，elevation_angle)以及观测特征量降采样DDM、功率校准DDM、信噪比和NBRCS(ddm_0，ddm，ddm_snr和NBRCS)。图5给出了典型的功率校准DDM，呈典型的马蹄形分布。NBRCS数据是用于反演分析的基础观测特征量，每个观测点对应一个7 delay×5 Doppler的二维数据，其中delay为-0.5 ～ 1 chip，0.25 chip分辨间隔；Doppler为-1.0～ 1.0 kHz，500 Hz分辨间隔。

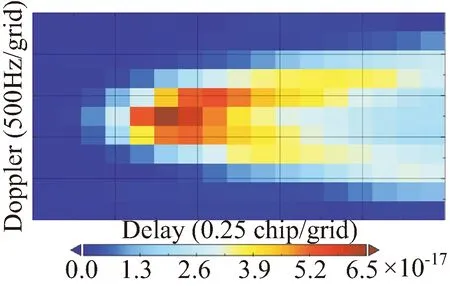
图5 典型的功率校准DDMFig.5 Typical power calibrated DDM

1级数据产品中A星和B星日均观测点数均约为6 000点，最高可到8 000点。反演建模中以2019年7～9月的数据作为建模数据集。图6给出了1级数据观测的洋面空间分布图。可以看出，捕风一号可实现±45°范围内的有效覆盖。图中颜色深浅代表了观测频次的大小，可见在当前的轨道设计下，在南北纬30°～45°之间观测的频次最高。相比较于CYGNSS，捕风一号可以获得更高纬度的观测数据。

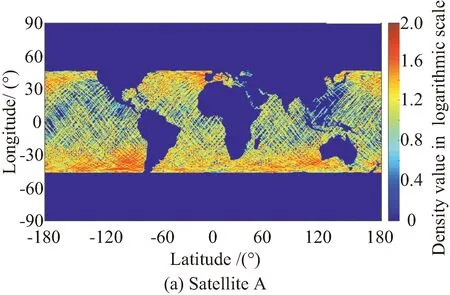
图6 2019年7月全月卫星数据观测区域及频次分布Fig.6 Satellite observation region and frequency distribution in the full month of July, 2019

3.3 基于GMF方法的经验模型构建

按理论模型，逐像元的NBRCS表征的是图2中的洋面特征量，在镜面点附近近似为一常数，但实际探测信号由于定标及噪声等因素，逐像元的NBRCS存在明显的数据波动。为此，综合考虑区域NBRCS均值及标准差，选取3 delay×5 Doppler区域的NBRCS均值作为反演建模分析观测特征量。

分析捕风一号1级数据中影响GMF建模的敏感性因素发现：除镜面点入射角因素外，不同卫星和不同增益天线明显影响NBRCS和风速之间的关系。图7给出了A星天线1和天线2在2个月时段内的数据对数密度图，可以发现在同样的参考风速段内，天线2得到的观测数据更为分散，直观可视。数据的分散性差异会直接影响GMF建模的模型参数值及模型参数误差大小。

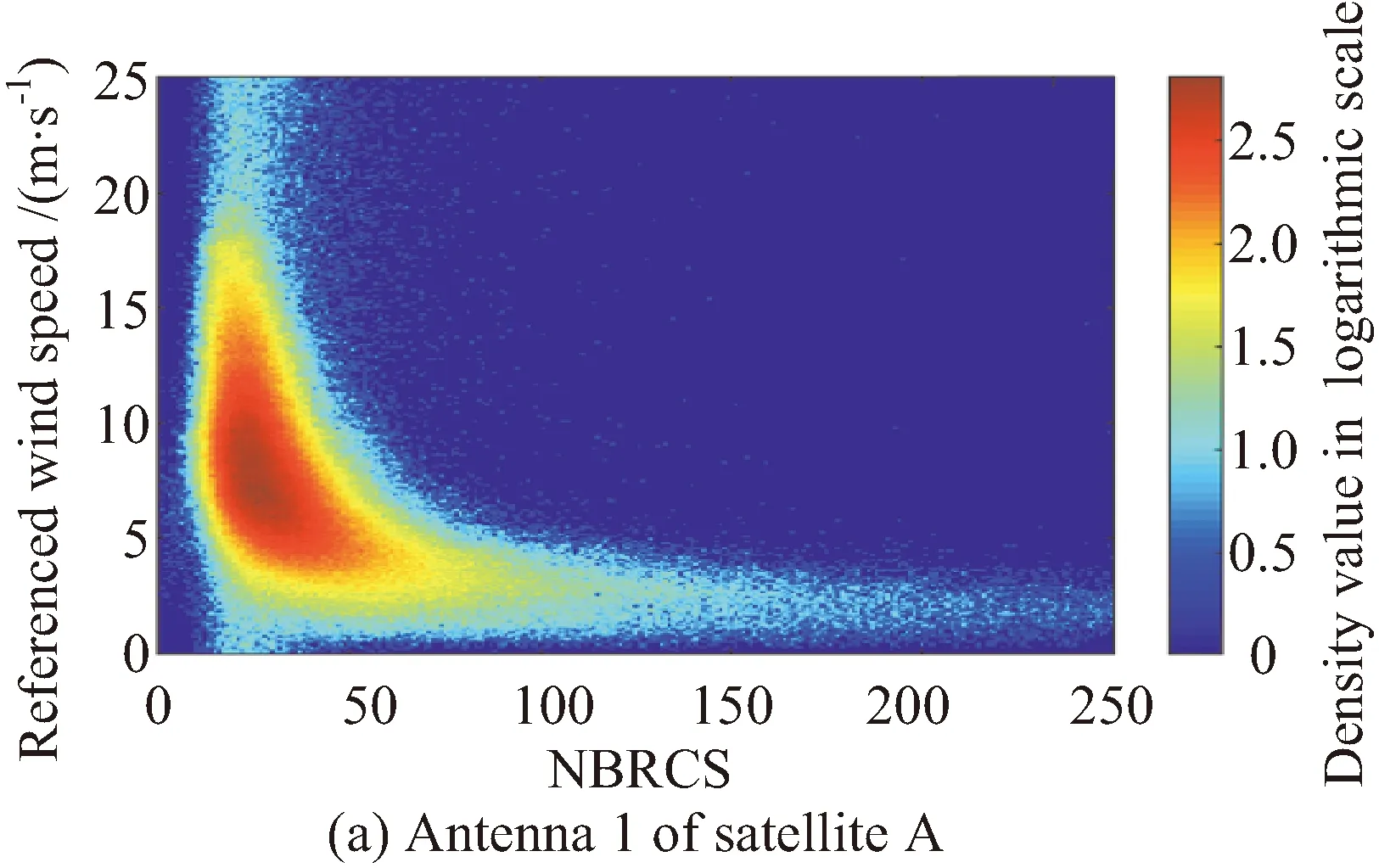
图7 2019年8～9月A星不同接收天线NBRCS与参考风速关系的对数密度图Fig.7 Log (density) scatterplot of NBRCS of satellite A antennas in August and September, 2019 vs. reference wind speed

为了直观展示由此带来的差异，图8给出了A星和B星不同天线数据在20°±2.5°镜面点入射角范围内的提取曲线。其中曲线上的数值点为各参考风速对应的实测NBRCS数据点均值。需要特别指出的是，当高风速对应NBRCS均值大于低风速对应值时，以低风速值替代，以保持曲线的单调性。对比图8可以看到，两星的天线2数据明显比天线1数据小，且B星两天线间数据的分离更为显著。据此，建模过程中，除了理论上需要按入射角分开建模外，还需要根据数据实际情况，对不同卫星、天线建立不同的GMF模型参数。

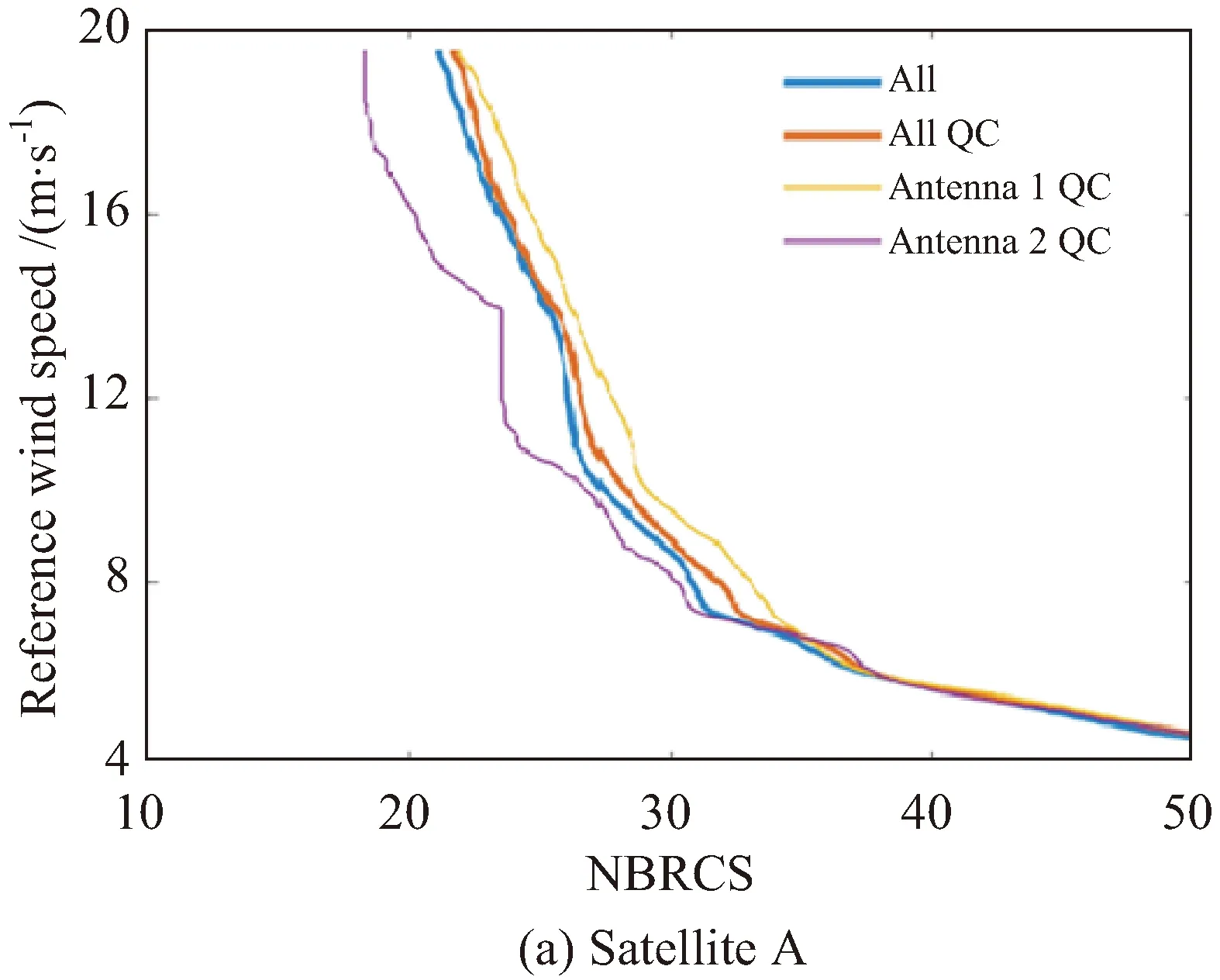
图8 A星、B星不同接收天线NBRCS与参考风速关系Fig.8 Relationship between NBRCS and reference wind speed of satellite A and satellite B with different antennas

进一步，分析观测数据SNR和参考风速关系，如图9所示，发现高信噪比数据对应低风速数据，而高风速数据则整体上处于低信噪比状态，SNR>4的数据表现出较好的综合曲线特征，但易缺失较大比例高风速数据。因此，建模过程中，按SNR对数据进行分组构建不同的GMF模型参数，能更好地体现观测数据特征。

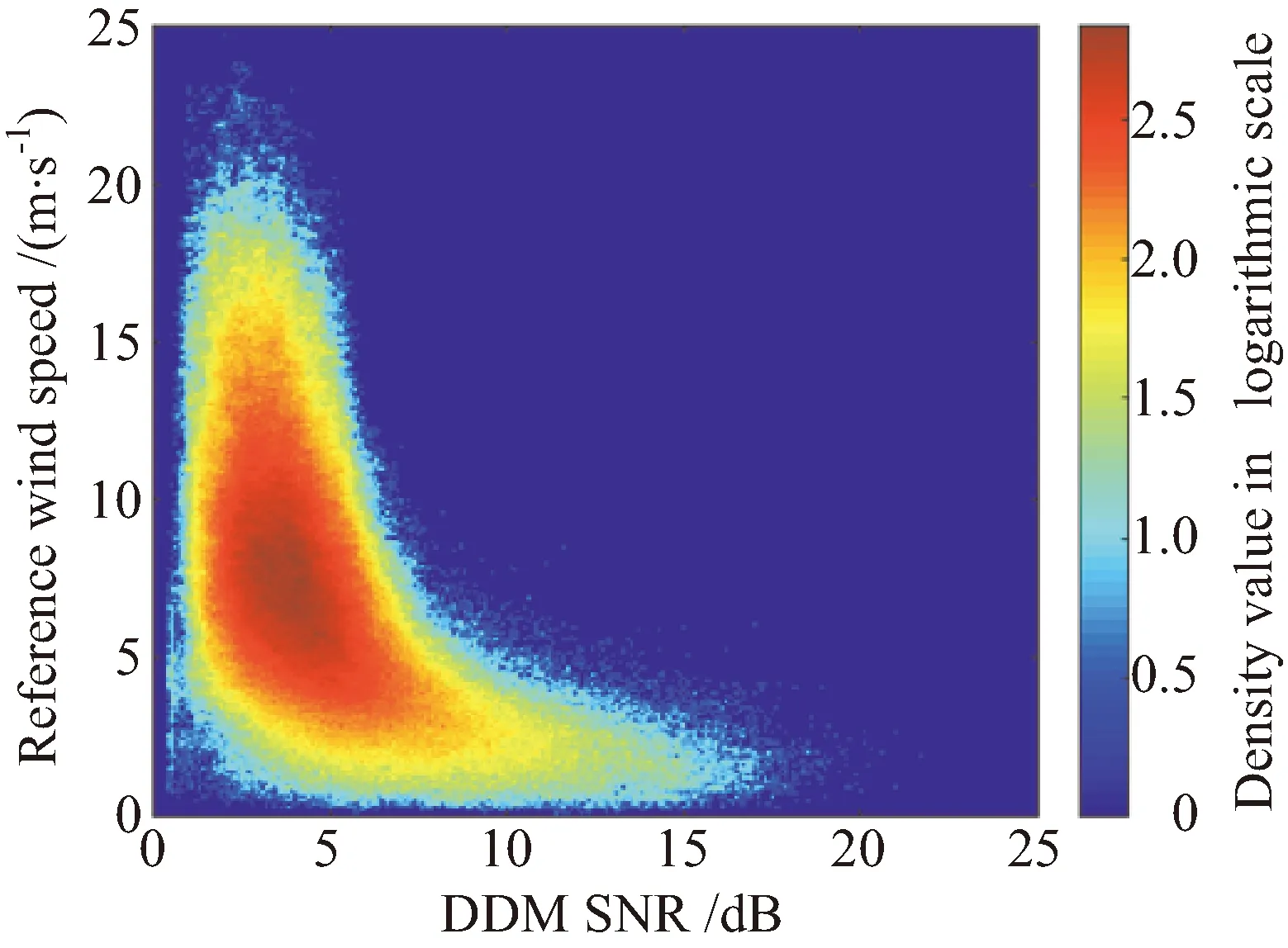
图9 DDM SNR与参考风速关系密度图Fig.9 Log (density) scatterplot of measured DDM SNR vs. reference wind speed

综上，考虑到现阶段数据的上述敏感性特征，本论文在CYGNSS按镜面点入射角建模的基础上，引入更多的建模细分，按卫星(A星/B星)、天线(1号天线/2号天线)和DDM SNR等影响因素进行分类筛选。实际建模过程，还包括以下几方面特色处理：1)为避免不同风速段建模数据量差异造成的模型对高风速段不敏感性，以参考风速值给定窗口(通常±0.5 m/s)内建模数据的NBRCS均值为该风速下特征值的表征，从而获得离散的特征数据点。2)为了进一步提升高风速段数据在建模中的有效性，在离散数据构建GMF参数化模型时，中低风速(<12 m/s)和中高风速(>10 m/s)独立构建模型，并以10～12 m/s区域为过渡区，通过两段拟合参数衔接获得最终的GMF模型数据。逻辑上，建模依赖的地面参考风速具有更小的误差，所以在模型建立过程，选用参考风速为自变量，观测特征量为应变量。中低风速段和中高风速段选用的GMF拟合函数分别如式(2)及(3)所示：

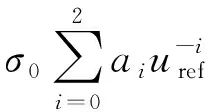
(2)

(3)

式中：σ0为NBRCS；ai，bi为模型参数；uref为参考风速。

图10给出了其中一个条件组合下的建模示例，其中对数密度图反映的是观测数据的实际分布，粉色曲线为提取出的离散的特征量统计表征值，黑色曲线为拟合得到GMF参数化模型曲线。图11给出了以A星天线1数据为例提取的不同角度离散特征值和GMF参数化模型曲线。总体而言，这种差异性与理论分析基本一致，且与CYGNSS相关数据处理理论与算法分析中反映的特征基本相符，说明可以以此进行捕风一号数据的风速反演。

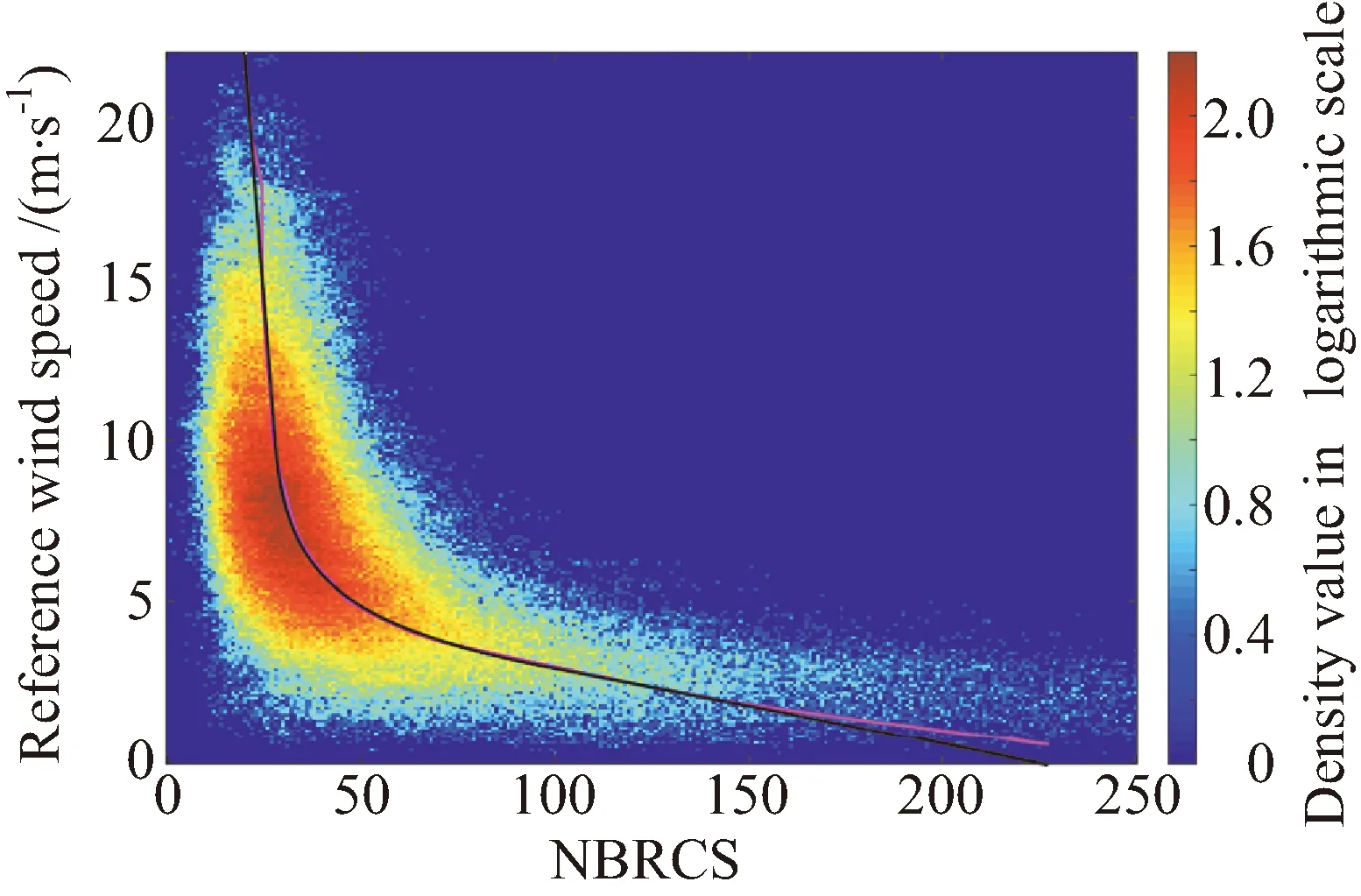
图10 GMF参数化曲线构建Fig.10 Diagram of GMF parameterized modeling

图11 A星天线1按镜面点入射角划分的GMF参量化曲线Fig.11 Discrete and continuous GMF curves with different specular incident angles for antenna 1 of satellite A

4 风速反演结果分析

利用模型构建导出模型参数，对捕风1级观测数据进行风速反演分析，此处以GNSS-R同类型观测模式CYGNSS的结果作比对来评估风速反演的性能。图12给出了反演获得捕风一号A、B双星及CYGNSS星座8颗卫星在2019年8月6日同一天内的观测结果。其中捕风一号数据采用NBRCS数据反演得到2级轨道数据，CYGNSS数据为融合NBRCS和LES观测量反演结果的3级网格风速产品。比对数据可以很明显看到两者数据具有很好的全局一致性，如日本东侧太平洋区域、马达加斯加岛附近有明显的低风速区域，孟加拉湾和西风带具有明显的高风速区域。需要指出的是，因为比对数据级别不同，时空对应关系也不能完全匹配，因此图12仅是一个定性的比对。对捕风一号卫星而言，可用于反演的反演特征量目前仅为NBRCS，反演数据质量分析也存在多方因素受限，数据产品中离散出现的高风速数据点较CYGNSS偏多，也制约了更为详尽的定量比对。后续尚需要提取更多的数据特征量和反演算法的持续改进。下文将主要从反演数据的统计特性上与CYGNSS作比对分析，间接验证本文的反演水平。

图12 捕风一号和CYGNSS同日(2019-08-06)观测反演数据比对Fig.12 Comparison of the retrieved wind speed of BF-1 and CYGNSS data in the same day (2019-08-06)

为了进一步展示本反演结果的统计特性，在此展示与CYGNSS ATBD[17]文档相对应的两组结果，并与之相对比。

图13给出了本文和CYGNSS ATBD利用NBRCS反演得到的结果与参考风速之差随镜面点入射角的变化特性对数密度图。其中颜色越暗红，表明这类结果出现的频次越高。图13(a)为捕风一号反演结果，(b)为CYGNSS L2 ATBD的结果。可以看到，两者反演结果的偏差趋势基本一致。两者反演风速偏差大部分落在±5 m/s的区域内，且两者反演风速大于参考风速的情况明显偏多。分析数据可以发现，这部分多出现于低信噪比和高风速情况。图10中目前的1级数据中低参考风速仍存有不少偏小的NBRCS值即直接造成大负偏差数据的产生。比较图13(a)和(b)还可以发现，捕风一号卫星反演数据在入射角10°～20°范围偏差相对偏大，这可能和载荷与卫星太阳翼间的相对关系有关。

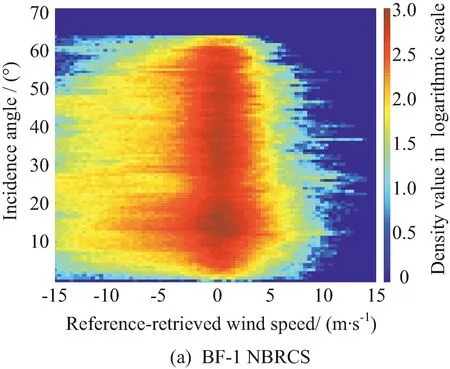
图13 反演偏差随镜面点入射角分布特性对比Fig.13 Comparison of retrieval deviation vs incidence angles of BF-1 NBRCS and CYGNSS result in ATBD

图14给出了不同参考风速对应的风速反演偏差特性，图中颜色表示数据的对数频次，其中(a)图为捕风一号，(b)图为CYGNSS L2 ATBD的结果。可以看到，与图13结果类似，两者反演结果的偏差趋势基本一致，在风速较低的情况下，反演偏差对称性较好，偏差比较集中；随着风速的提高，风速偏差分布也逐渐增大。这与两方面因素密切相关：1)NBRCS特征观测量变化灵敏度降低，无论图3理论分析还是图10实际数据特征，都表明在高风速时NBRCS特征观测量随风速变化趋于陡直，变化不明显；2)观测数据信噪比降低，高风速信号散射明显，NBRCS特征量值较小，从而造成探测信噪比下降，如图9所示，普遍低于5 dB。上述两个因素造成NBRCS特征量相对误差明显，进而体现到风速偏差分布显著增大。对比(a)图和(b)图可以看出，本文针对捕风一号数据特征，引入比CYGNSS更多的建模分类因子，以增加模型复杂性和牺牲模型适用性为代价，得到反演结果的整体分散性略优。后续针对1级数据的高精度定标，特别是在低信噪比区域，减小定标误差，将是提升反演性能重要切入点之所在。