航天员失重环境下运动策略与效能分析
2022-04-20李志昌黄倬然李剑飞曹哲魏承
李志昌,黄倬然,李剑飞,曹哲,魏承,*
1. 北京大学人民医院骨关节科,北京 100044
2. 哈尔滨工业大学 航天学院,哈尔滨 150001
3. 北京空间飞行器总体设计部, 北京 100094
4. 中国航天科工集团有限公司,北京 100048
1 引言
中国空间站天和核心舱发射升空,准确进入预定轨道,任务取得成功标志着中国空间站工程在轨建造大幕正式开启。中国空间站在后续进行在轨组装建造、空间实验平台搭建与研究、空间站维护维修和应急安全任务时都会涉及大量载人航天活动。空间站为航天员提供更大活动空间,因此也对航天员空间活动提出了更多需求。与地面环境不同,由于空间为微重力环境,航天员空间活动与地面活动动力学特性存在差别。在制定载人航天任务以及进行航天员训练时必须要考虑力学环境特点,需要以航天员为对象进行动力学实验研究[1-3]。
航天员的动力学特性研究是一种在特殊环境下对人体力学行为的研究。人体的研究由于受到实验条件、成本、伦理等限制经常需要依靠计算仿真。在人体动力学仿真计算方面,近年来主要围绕基于骨骼关节建立的人体多刚体模型,基于骨骼-肌肉结构建立的人体生物力学模型以及基于神经-肌肉-骨骼建立的力学-控制综合模型三个方面进行了大量研究。如秦菲菲等基于UK(Udwadia-Kalaba)理论建立人体下肢刚体模型[4],对下肢运动过程关节力矩进行分析;Lee S H等考虑软组织应变而耦合有限元单元建立人体上半身骨骼-肌肉综合生物力学模型,并设计控制器计算出必要的肌肉激活信号[5];Dzeladini F等考虑人体神经反射效应建立基于反射的神经肌肉模型,评价其在人体行走过程中的调节作用[6];Joo H. Kim等基于优化算法对人体运动动力学进行预测和分析,说明了不同的外部负载和任务导致了不同的人体运动和执行器扭矩分布[7]。总体而言,近年来对人体动力学的理论研究愈发完善,相关生物力学理论以及控制思想也大量应用于机械仿人机器人领域[8-9]。
国内人体动力学在航天中的应用,主要体现在航天服外骨骼开发、航天员地面模拟方法以及针对航天员局部简单活动的仿真[10],譬如李照阳等设计了航天服关节助力外骨骼结构并优化[11];李昊等以搬运载荷为例,针对航天员舱外作业过程进行了动力学仿真等,对航天员失重状态下全身协调运动以及自身姿态调整方面研究较为有限[12]。
近年来随计算技术的发展,许多计算工具被开发用于模拟仿真人体自然运动,如LifeMod、SIMM、AnyBody等商业软件以及开源软件OpenSim。这些商业软件目前广泛应用于跟踪描述人体运动行为、计算人体动力学特点、分析正常和病态生理现象[13-15]。然而,由于商业软件可能存在的使用限制以及OpenSim在与环境交互时对实验的依赖,本文基于多体系统动力学软件(MBDyn)[16]建立微重力环境航天员多体系统动力学模型,分析空间环境下航天员运动的动力学特征与姿态调整策略,拓展MBDyn在人体动力学仿真方面应用。
2 航天员微重力环境虚拟人体模型
人体运动由多个骨骼、关节、肌肉、软组织同时共同作用而成,因此为实现对人体运动的跟踪、定量描述,就需要对人体系统进行分析简化并抽象出可计算的多体系统动力学模型。
2.1 人体系统空间姿态及运动学描述
为统一运动描述,首先对空间惯性坐标方向进行规定。根据人体的运动规律,一般将人体在三维空间内划分矢状面(XOY)、额状面(YOZ)和水平面(ZOX)三个相互垂直的基准面,从而对应将基准面交线矢状轴(X)、垂直轴(Y)和额状轴(Z)作为基准轴。
本文的研究对象为整个航天员人体系统,根据航天员身着航天服时的空间运动状态,忽略手指、脚趾等小关节对系统运动影响,考虑上肢的肩、肘、腕关节以及下肢的髋、膝、踝关节对人体自由度进行分配。人体肩、髋关节可进行屈曲/伸展、外展/内收、内/外旋活动,可抽象为球铰链接,具有三自由度;肘关节、膝关节主要进行屈曲/伸展活动,可抽象为转动副,具有单自由度;踝关节主要可实现屈伸同时也可实现内旋外展,因此分配二自由度。综上,规划出人体上肢单臂七自由度、下肢单腿六自由度模型,结合本文主要涉及航天员肢体简单运动,忽略肩关节内外旋活动,进一步简化肩关节为二自由度。最终建立人体四肢二十四自由度模型如图1,其中关节内数字为自由度数目,人体可视化模型来源于OpenSim人体骨骼几何模型,相关动力学参数配置见表1。

图1 人体运动学描述Fig.1 Description of human kinematic

表1 人体骨骼模型动力学参数
2.2 人体动力学建模
定义躯干为漂浮基座,在骨骼质心、关节、末端设立坐标系,建立树状结构计算模型。通过沿X、Y、Z轴平移及绕轴转动的6个参数对模型进行运动学描述,并计算相应坐标变化矩阵。多个自由度的实际关节由多个长度、质量均为0绕其坐标系Z轴运动(转动/平移)的单自由度计算关节表示。


式中:γj、βj、αj分别为绕各主轴姿态变换角度;qj为关节i的旋转角度。当基座的速度v0与角速度ω0给定后,可以通过递归算法得到速度和角速度,求导后可得相应关i的速度vi及角速度ωi:
式中:cij为质心i到关节j位移;vBi,ωBi分别为骨骼i连接的上一骨骼的速度及角速度。整理后可得末端速度xe的雅克比矩阵,其中Jm为关于关节角q的雅可比矩阵,Jb为关于躯干位姿xb的雅可比矩阵:
单个刚体的受力情况由Newton-Euler方程得出,Fi为力矢量,Ni为力矩,mi、Ii分别为骨骼i的质量和转动惯量:
定义Bi为骨骼i连接的上一个骨骼的编号,则骨骼间连接关系可表示为:
从末端向基座逆向迭代后可得各关节广义力:
式中:fj和ni为作用在关节i上的力和力矩;fe和ne为作用在末端关节上的力和力矩。最终模型的动力学方程可以表述为:
式中:Fe为末端外力/力矩;cb,cm为速度相关非线性项;Fb/τ为基座上外力/力矩;其余各项表示为:

式中:r0i≡ri-r0∈R3;ri为骨骼i质心位置;HMq表达式为:
式中:JRi≡[k1,k2,…,ki,0,…,0]∈R3×n;ki为关节i轴线方向向量;JTi表达式为:
JTM表达式为:
2.3 基于逆动力学控制器设计
基于公式(1)可移项得到关节力矩:
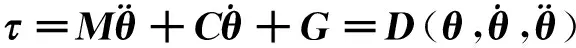

系统误差在计算模型与实际模型完全一致的情况下,各关节误差解耦可表示为:
综合以上动力学与控制理论建立航天员动力学与控制系统如图2,其中基于逆动力学计算出的关节力矩项输入MBDyn,在MBDyn中进行动力学求解得到关节实时运动数据,再由运动数据计算反馈项完成系统的闭环控制。
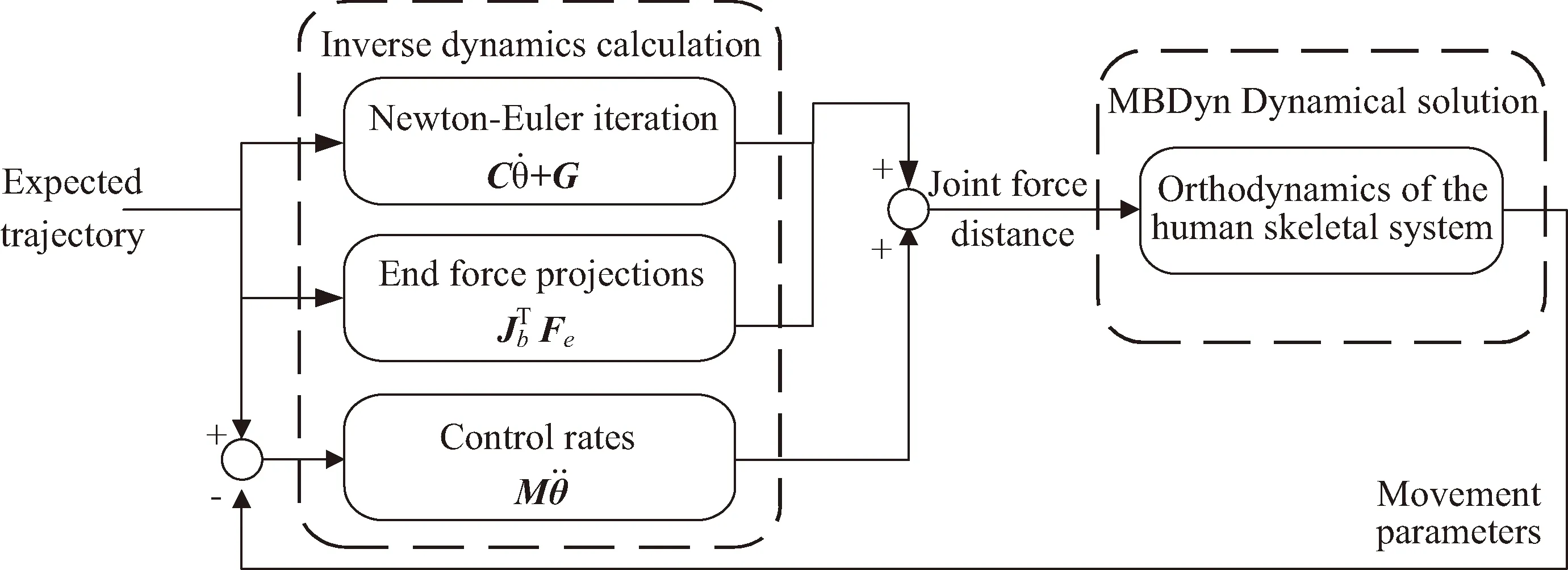
图2 系统动力学-控制流程图Fig.2 Dynamics - control flow diagram
2.4 动力学-控制系统验证
相较于逆动力学计算,闭环控制系统可通过负反馈修正误差,抗干扰能力强,控制精度较高[17-18]。首先利用人体蹲起这一简单全身运动过程,对2.2节中闭环系统的控制精度进行验证:
通过对蹲起过程仿真计算,人体上下肢期望运动,与实际控制跟随效果的对比曲线分别为图3、图4。由曲线重合程度可以看出,上述控制系统对期望运动全过程的跟随效果较好,系统的精度较高。

图3 上肢关节角度曲线Fig.3 Upper limb joints angle curve

图4 下肢关节角度曲线Fig.4 Lower limb joints angle curve
3 航天员姿态调整策略分析
3.1 单个肢体简单调节
航天员在空间运动中由于微重力环境,在不接触航天器时身体会处于漂浮状态,因此身体运动规律与地面条件有所区别,需要依靠自身动作来对姿态进行调节。
根据质心动量矩定理,处于空间自由状态的人体可以通过肢体的摆动来实现对姿态的调整或保持运动稳定,因此本文首先对人体上肢活动对躯干姿态的影响进行定量分析。
设计人体右臂首先绕肩关节由自然下垂摆动至身体侧方平举,之后右臂保持与躯干90°绕垂直轴方向旋至身体前方,上述过程如图5,具体关节角度变化如图6所示。

图5 肢体简单调节示意Fig.5 Simple limb adjustment diagram

图6 关节角度曲线1Fig.6 Joint angle curve 1
经过仿真计算得到运动过程中人体躯干姿态变化如图7,对比肢体运动与姿态变化曲线可以看出,右上臂分别通过沿x轴外展和沿z轴内旋可以实现对躯干延矢状轴和额状轴滚转和偏航的调节。同时由于人体自身结构所致延矢状轴方向转动惯量相比Y轴方向明显较大,因此手臂调节躯干进行绕Y轴的偏航作用较为明显,且手臂侧摆动作也会引起其他方向姿态偏移。

图7 躯干姿态角度变化曲线1Fig.7 Torso posture angle change curve 1
3.2 全身肢体协调姿态调整
(1)肢体协调躯干绕额状轴方向运动
通过上述分析说明了肢体对航天员姿态的可调节性,但同时从结果也可看出肢体对除垂直轴外的其他方向姿态调整能力有限,因此需依靠四肢协调运动而实现航天员姿态较大幅度改变。
参考相关文献[19]设计运动过程如图8所示,首先双臂侧平举过头顶同时小腿向后方摆动,之后大腿内收蜷至胸前后小腿向外伸展,随后双臂沿侧方摆回身体两侧,最后双腿展开伸直至动作完成,具体关节角度变化如图9所示。
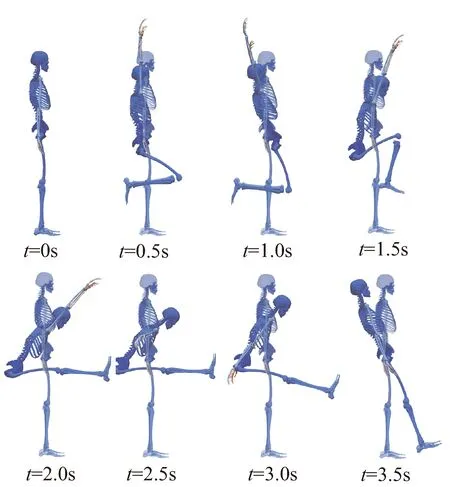
图8 人体四肢协调运动示意1Fig.8 Diagram 1 of coordinated movement of human limbs

图9 关节角度曲线2Fig.9 Joint angle curve 2
经过仿真计算,上述运动过程躯干姿态变化如下图10所示,由图所示通过以上肢体组合动作最终可使人体躯干在额状轴方向偏移20°左右,并且由于人体以额状面为对称面进行动作,且双臂在运动中起到一定平衡作用,相较于单肢体调整,躯干另外两个未调整方向姿态角度偏移较小。
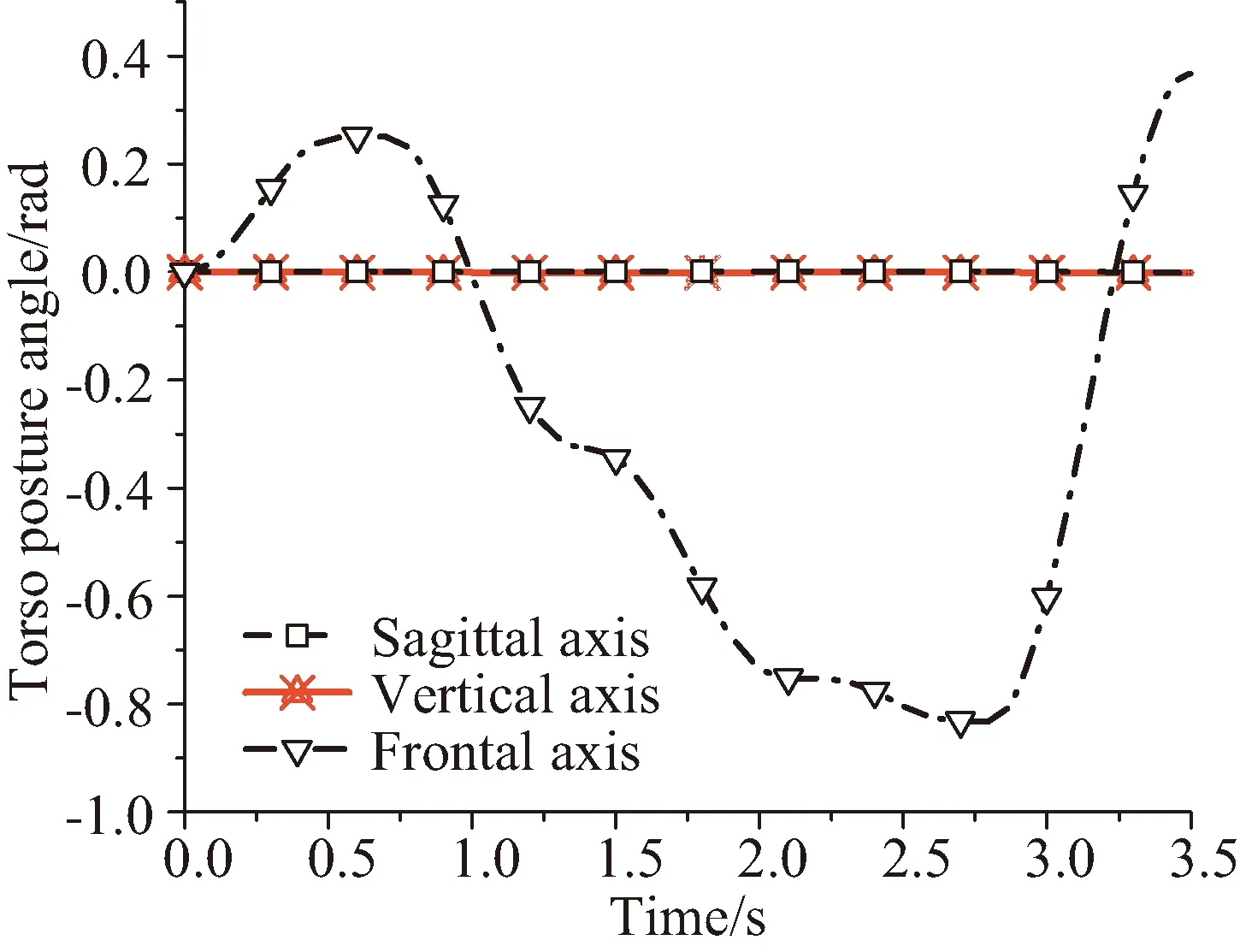
图10 躯干姿态角度变化曲线2Fig.10 Torso posture angle change curve 2

图11 关节力矩曲线1Fig.11 Joint torque curve 1

图12 关节功率曲线1Fig.12 Joint power curve 1
(2)肢体协调躯干绕矢状轴方向运动
由于人体质量分布整体绕矢状轴方向惯量较大且腿部关节在绕矢状轴方向自由度存在约束限制,人体绕矢状轴方向调节较为困难。根据对图11、图12中髋关节的力矩特点分析,设计人体下肢屈膝蜷在身前减小惯量,由双臂在身侧摆动调节运动方向,具体运动过程如图13所示。
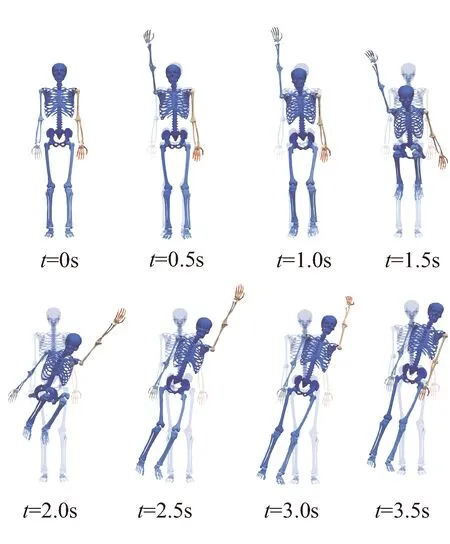
图13 人体四肢协调运动示意2Fig.13 Diagram 2 of coordinated movement of human limbs
图14为关节角度曲线,图15为人体躯干姿态角度曲线,从图中可以看出,通过上述运动规划最终可使躯干绕矢状轴偏移30°左右,但由于人体结构以及运动过程沿额状面的非对称性在运动过程中姿态在其他方向也存在偏移。

图14 关节角度曲线3Fig.14 Joint angle curve 3

图15 躯干姿态角度变化曲线3Fig.15 Torso posture angle change curve 3
计算得到图16、图17关节力矩及关节功率曲线,对比可得相似膝关节力矩、功率小于髋关节的结论,同时由于屈膝动作使得髋关节运动功率明显降低,肩关节在力矩和功率消耗相近的条件下使得躯干角度偏移更明显。

图16 关节力矩曲线2Fig.16 Joint torque curve 2

图17 关节功率曲线2Fig.17 Joint power curve 2
4 结论
本文针对航天员在空间微重力特殊环境下的姿态调整问题,首先建立了人体系统动力学与控制计算模型,其次对航天员通过肢体按相关运动策略进行姿态调整的过程依靠动力学模型仿真进行验证。仿真显示了:
1)人体依靠单肢体的简单调节以及四肢的协调运动均可实现无外力驱动下躯干进行一定程度的姿态主动调整。
2)对比各运动关节的力矩、功率曲线说明了在相同直臂条件下,腿部髋关节力矩大于上肢肩关节,对于同一肢体上不同位置关节,靠近躯干的关节力矩更大。因此在航天员关节助力设备设计时可针对受力较大关节进行助力设计。
3)屈膝动作可有效减小人体髋关节在抬腿过程的力矩及功率并且使上肢对躯干绕矢状轴方向的调整作用更为有效。
本文基于MBDyn建立了人体系统动力学模型,对微重力环境下航天员姿态调整策略进行了动力学验证。所得到的相关人体运动规律及动力学特点对后续载人航天中任务动作设计具有一定的参考意义,后续可围绕运动稳定性、人体建模精确性以及人-机交互等方面进行进一步的完善和深入研究。
