基于N-BEATS的单站对流层天顶总延迟预报

苏行，杨韬，孙保琪，杨旭海

1. 中国科学院 国家授时中心，西安 710600

2. 中国科学院 精密导航定位与定时技术重点实验室，西安 710600

3. 中国科学院大学，北京 100049

4. 西北工业大学 无人系统技术研究院，西安 710072

1 引言

全球导航卫星系统(global navigation satellite system，GNSS)参数估计中，对流层延迟与测站钟差、测站高程强相关[1]，是GNSS数据处理中最重要的误差源之一。信号传输过程中，由对流层引起的信号时延一般称为对流层延迟。不同高度角的对流层延迟通常可由对流层天顶延迟与相应的映射函数计算而来。对流层天顶总延迟(zenith total delay，ZTD)主要由天顶干延迟(zenith hydrostatic delay，ZHD)和天顶湿延迟(zenith wet delay，ZWD)两部分组成[2]。与水汽强相关的ZWD变化幅度较大，而ZHD较为稳定。因此在实际应用中，通常将ZWD作为未知参数来进行估计[3]。而高精度的对流层延迟先验值有助于参数估计的快速收敛[4]，从而提升其在实时应用中的可能性[5]。

目前，通过使用事后精密产品进行精密单点定位解算，国际GNSS服务(international GNSS service，IGS)可提供数据间隔为300 s的对流层ZTD事后精密产品。包含350余个IGS跟踪站的对流层ZTD及其水平梯度分量，产品延迟约为3周[6]。维也纳科技大学基于高精度ECMWF气象数据库[7]，提供数据间隔为6 h，以地表为基准的VMF1[8]及VMF3[9]事后格网对流层产品，包含ZHD、ZWD及其映射函数系数，其中VMF1的分辨率为2°×2.5°，VMF3的水平分辨率为1°×1°，该格网产品的延迟为1 d。

为了满足实时、近实时的需求，通常使用经验模型来进行先验对流层延迟建模，常见的有GPT及其映射函数GMF[10]、GPT2[11]、GPT2w[12]、UNB3m[13]等。此外，基于ECMWF高精度预报产品，维也纳科技大学提供了对流层预报格网产品VMF1-FC[14]，预报范围为42 h，数据间隔为6 h。

大气中水汽含量变化迅速且幅值不定，因此对流层产品的时间分辨率越高，越适合于实时应用。利用传统回归方法可设计手工特征学习有效模式，而基于数据驱动的深度学习，通过大量有标签样本，可端到端进行模式学习，规避传统建模中的手工特征提取，即基于大量训练样本，学习较难建模的特征。本文基于高精度高分辨率气象数据库，利用深度学习N-BEATS算法，进行时间分辨率为2 h的对流层ZTD短期预报研究，并进行了精度评估。

2 N-BEATS算法

经典的时间序列预测方法，例如自回归滑动平均模型(ARMA)和差分整合滑动平均自回归模型(ARIMA)，要求时间序列数据具有平稳性或者微分后是平稳的。 本质上，此类方法只捕获线性关系。近年来，随着算法的进步和计算机算力的提升，深度学习方法强大的自动模式学习能力和非线性函数拟合能力逐渐凸显，在许多领域的性能都优于传统方法，例如计算机视觉、语音识别、自然语言处理和时间序列预测。包括卷积神经网络(CNN)[15-17]、递归神经网络(RNN)[18]和注意力机制[19]在内的经典神经网络模块均被用于时间序列预测。

最近，基于神经网络基底扩展分析的可解释的时间序列预测(neural basis expansion analysis for interpretable time series forecasting，N-BEATS)在几个著名的公开数据集上显示出优于其他时间序列预测方法的性能[20]。N-BEATS的网络结构可以快速训练并使神经网络具有一定的可解释性。

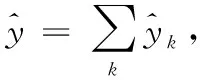
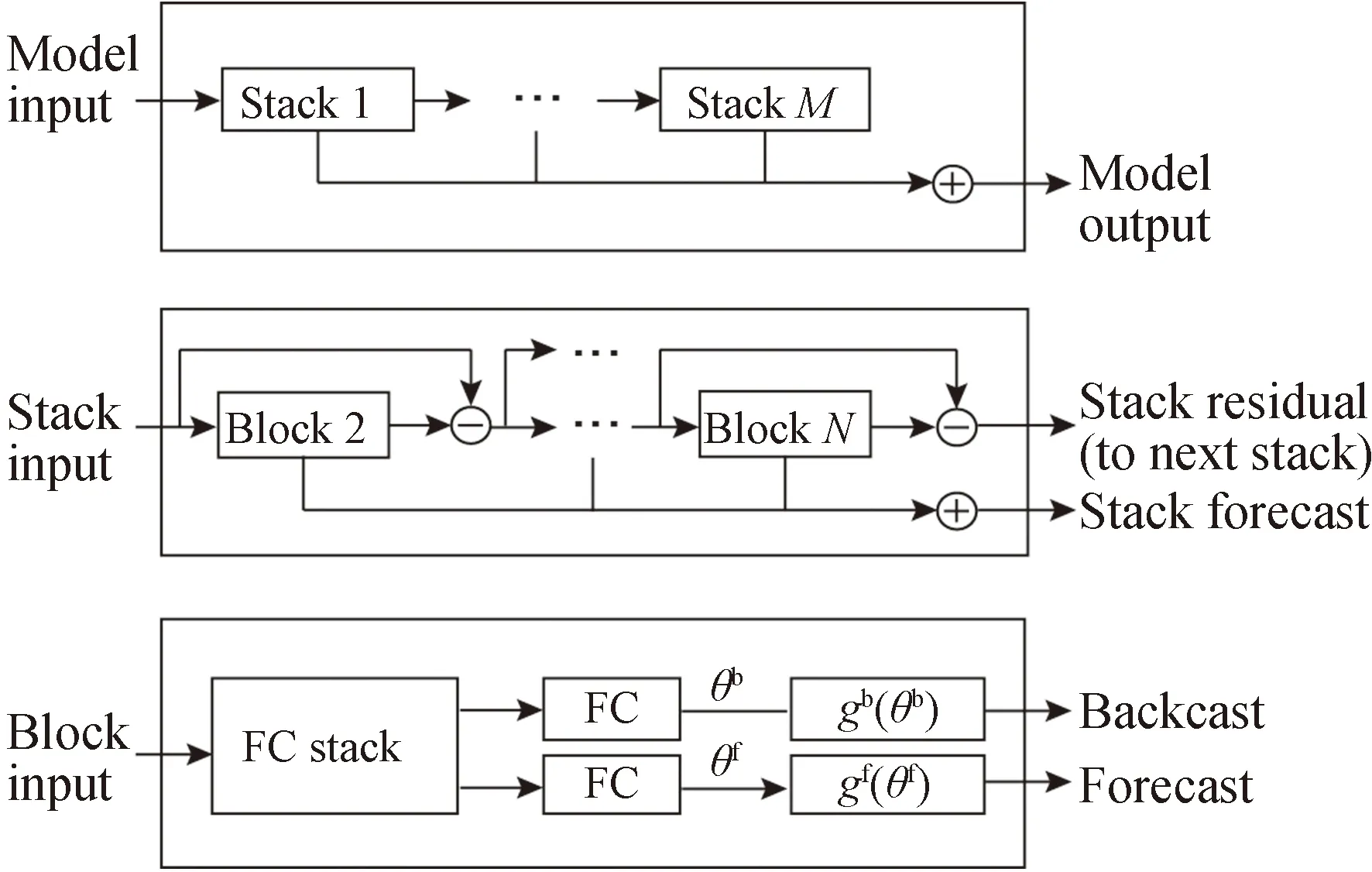
图1 N-BEATS网络结构Fig.1 The network architecture of N-BEATS

3 ZTD预报试验设计

3.1 数据源

本文使用的高精度高分辨率对流层延迟数据来源于捷克Pecny天文台GOP-TropDB对流层气象数据库[21]。GOP-TropDB基于ECMWF的再分析数据库ERA-Interim[7]，为用户提供对流层相关气象参数，避免了用户直接从ECMWF获取气象参数时面临的巨大数据量及复杂的数据处理。由于深度学习的模型训练特点是基于大量数据来进行特征提取，数据量越大越有利于特征的提取。因此本文选取了较长数据弧段，即2002年1月1日至2019年6月30日，采样间隔为2 h，研究对象为9个在全球分布较为均匀的IGS跟踪站，如图2所示。其中，HARB和KOKB的测站高程高于1 000 m，分别为1 558 m、1 167 m，WTZR高程约为666 m，其余6个测站均低于200 m。

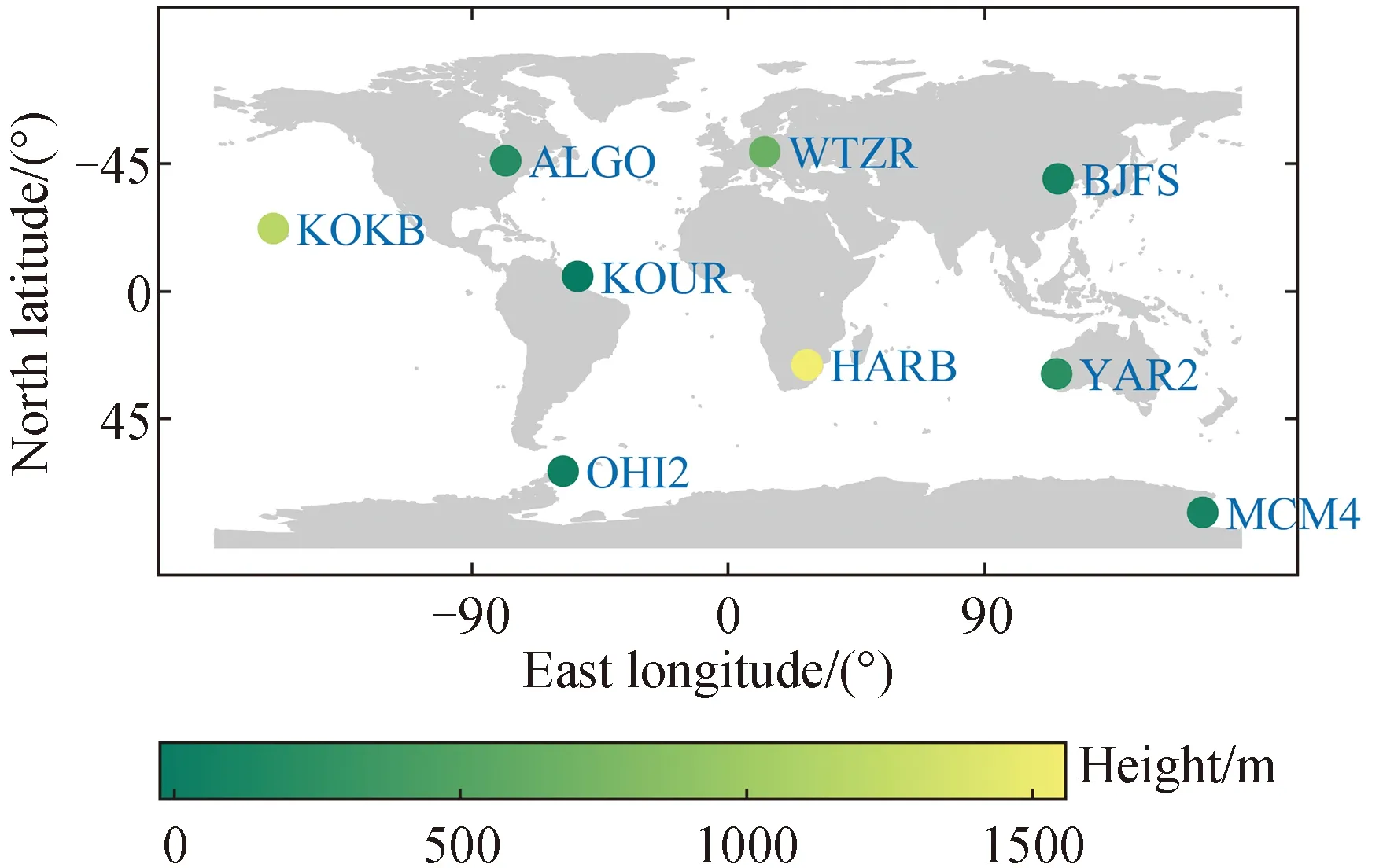
图2 9个IGS跟踪站椭球高程及分布Fig.2 Global distribution and ellipsoidal heights of 9 IGS tracking stations

3.2 基于N-BEATS的ZTD预报策略

在模型搭建中，根据实测数据的规律，可基于N-BEATS进行趋势项及周期项模型的混合搭建。首先针对所选测站的ZTD序列进行快速傅里叶变化，以进行周期项的探测。结果表明，除了周年项、半周年项此类长周期项以外，还存在多个短周期项，例如与地球自转相关的24 h周期项、与月球潮汐相关的12 h短周期项。在本文的模型搭建中，根据不同周期项对各站影响的显著性，为各站设定不同的周期项个数。此外，经验证，趋势项采用默认值即可。

模型搭建好之后，进行输入及预报步长的设定，本文针对分辨率为2 h的24 hZTD预报，根据输入弧长设计了3种ZTD预报策略，如表1所示，以2 h为滑动窗口，分别以24 h、48 h、72 h为输入步长，进行以24 h为步长的预报，示意如图3所示。

表1 三种策略的输入及预报弧段设置

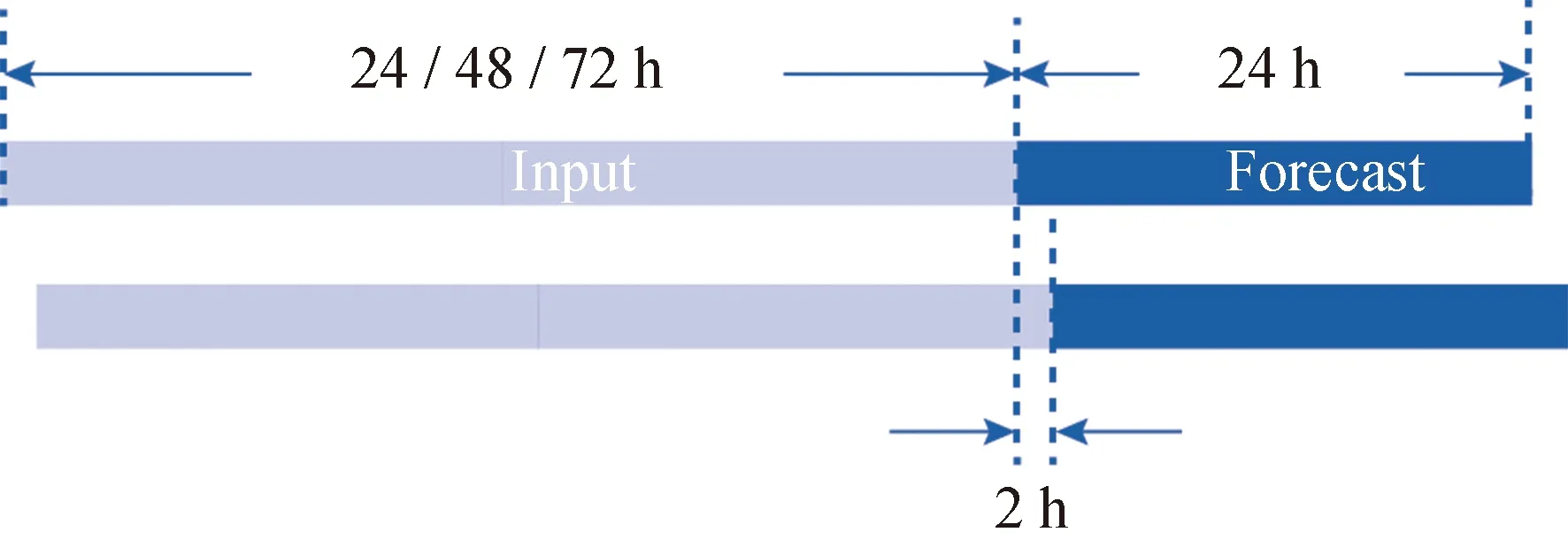
图3 预报策略示意Fig.3 Schematic diagram of forecast strategy

随后确定学习率，学习率决定了目标模型的收敛速度及精度，经试验，本文选取的学习率为0.000 1。最后通过大量数据样本进行模型训练。以2018年7月1日为分界，将数据分为训练数据集和验证数据集。模型的训练将在训练集上进行，由此训练出的模型在验证集上进行验证。以图4中 BJFS站对流层ZTD时间序列为例，取最后一年为验证集(红线)，时段为2018年7月1日至2019年6月30日，其余时段(蓝线)为训练集。

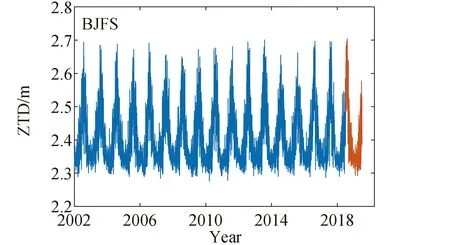
图4 训练集与验证集示意Fig.4 Schematic diagram of training set and validation set

4 ZTD预报精度评估

4.1 重复性评估

为了衡量该算法的鲁棒性，针对BJFS站ZTD，使用3种策略，各重复训练了9组模型，对该算法进行了重复性评估。

选取了连续365 d的ZTD预报值进行预报精度的重复性评估。图5为该365 d预报序列的示意。弧段从2018年7月1日至2019年6月30日。以24 h为边界，将每天0点的24 h预报值拼接为365 d的预报值。

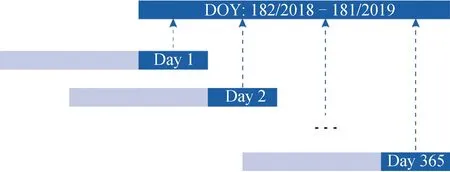
图5 365 d预报序列示意Fig.5 Schematic diagram of 365 days forecast

将ZTD预报值与真值相减得到残差序列，表2为S1、S2、S3三种策略各自所训练的9组模型的365d残差序列的均值及其STD(standard deviation)。图6为3种策略各9组残差序列均值(左)和STD(右)的箱图。可以看出，残差序列的均值大多在亚毫米量级，STD大多约为27～28 mm。由此可见，该算法具有较为稳定的重复性。

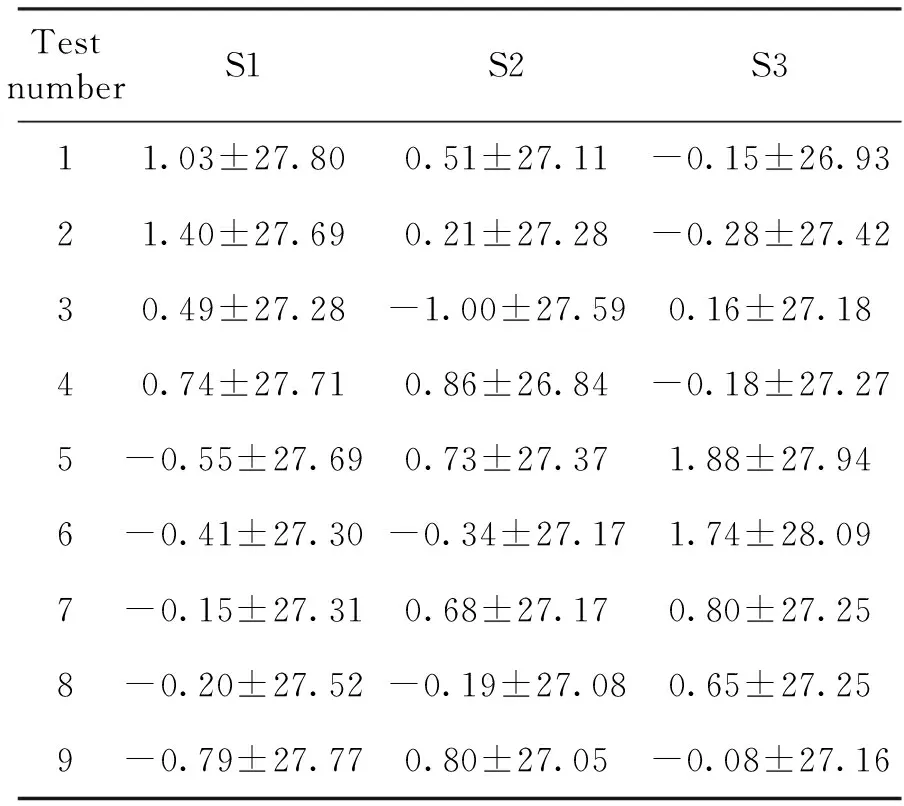
表2 9次365d预报均值及其STD的统计结果

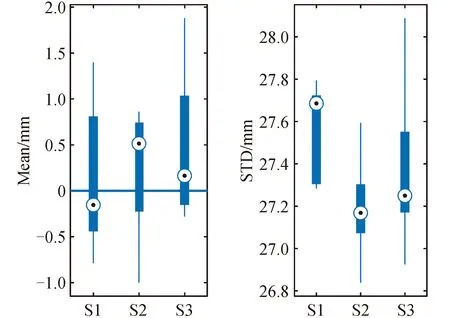
图 6 三种预报策略的均值与STDFig.6 Mean and standard deviation of 3 forecast strategies

4.2 不同弧段ZTD预报精度评估

第4.1小节的结果表明，该算法具有较为稳健的重复性。本小节针对不同策略，对选取的9个IGS跟踪站的ZTD，进行不同预报弧段的精度评估。由于预报策略为每2 h进行一组预报，且每组以2 h为间隔，预报24 h，将每组的第0、2、4、…、22小时的2 h预报数据分别进行拼接得到2018年7月1日至2019年6月30日共365 d的预报值。示意如图7所示，图中以第2小时的2 h预报值所拼接的365 d预报时序为例，称之为4 h 365 d预报时序。

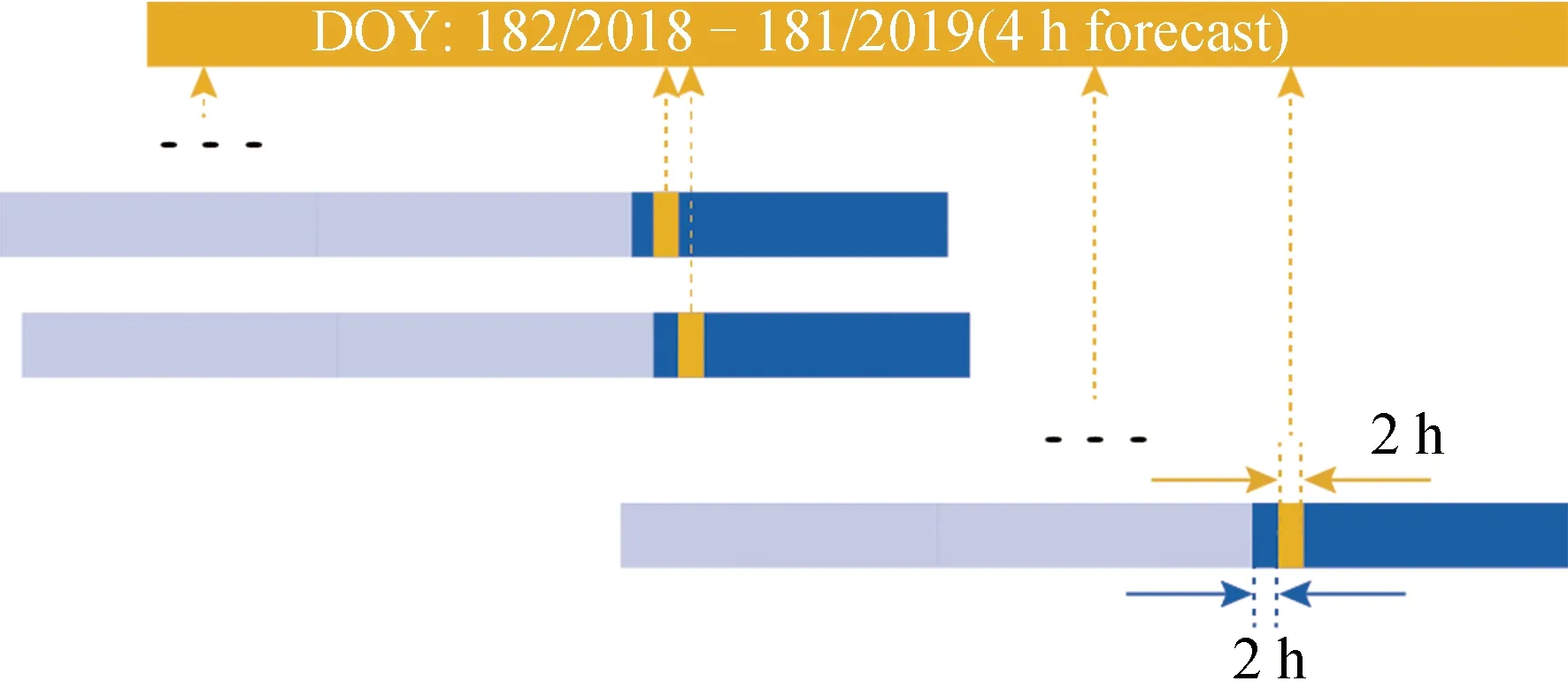
图7 4 h 365 d预报序列示意Fig.7 Schematic diagram of 365 days forecast of the 4th hour

(1)残差序列均值

对9个跟踪站的ZTD使用S1、S2、S3三种策略的不同弧段拼接所得的365 d预报值的预报残差均值进行评估。3种策略不同弧段的预报残差均值的统计结果如图8所示。

从图8中可以看出，策略S1中，有个别跟踪站诸如BJFS、HARB、KOUR的残差均值随着预报弧段的增加没有明显的起伏变化，但整体上随着预报弧段的增加，9个跟踪站的残差均值呈发散趋势，6 h以内的预报残差均值可小于1 mm。策略S2中，除了YAR2站的预报残差均值随着预报弧段的增加有明显的发散趋势，其余跟踪站的预报残差均值的波动大约在2 mm以内。策略S3中，随着预报弧段增加，YAR2站的预报残差均值依然比较发散，其余跟踪站预报残差均值的波动大多在1 mm以内。

图8 分别使用S1、S2以及S3策略所得的第N小时预报值的全年残差均值Fig.8 Mean of the Nth hour forecast residuals of 365 days using strategy S1, S2 and S3

由此可见，随着预报弧段的增加，预报残差的均值越发散；用于预报的输入弧段越短，随着预报弧长的增加，预报弧段残差均值越发散。策略S3性能良好，但同时需要较多数据量。表3为所有站不同预报弧段的预报残差绝对值的均值，可以看出，总体上，3种策略的24 h内预报值均小于3 mm，12 h内的预报值大多优于1 mm；6 h内的预报精度均可达亚毫米量级。

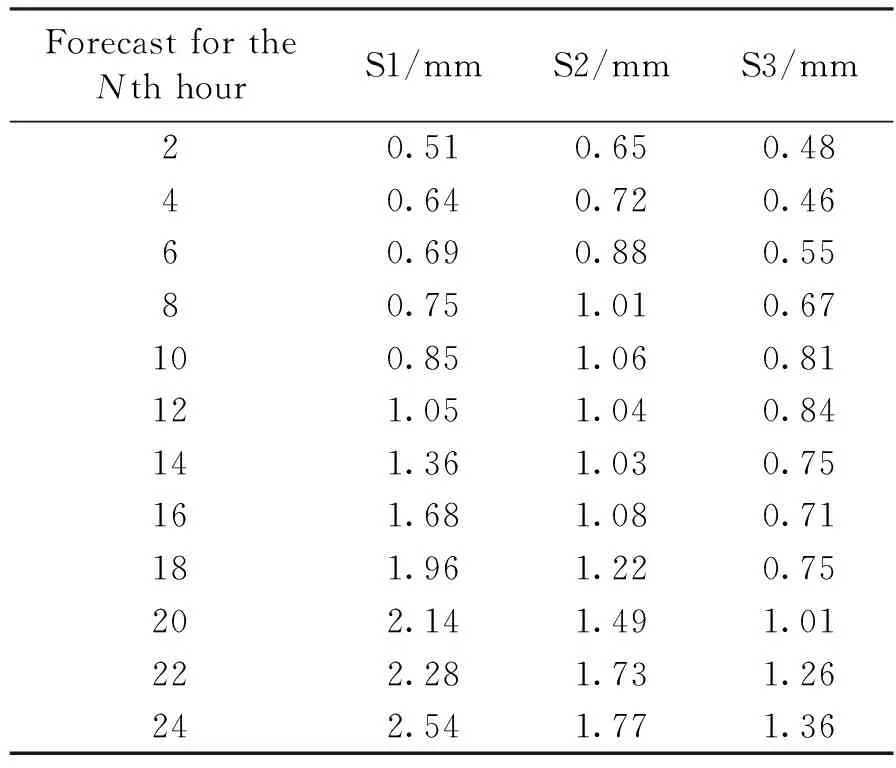
表3 九个站不同预报弧段预报残差绝对值的均值

(2)残差序列的标准差

本小节对9个跟踪站3种策略的ZTD预报残差序列的标准差进行评估。图9为策略S1、S2、S3对应的不同预报弧段的预报残差STD统计结果。

图9 分别使用S1、S2以及S3策略所得的第N小时预报值的全年残差STDFig.9 STD of the Nth hour forecast residuals of 365 days using strategy S1, S2 and S3

从图9中可以看出，随着预报弧长的增加，ZTD预报残差的STD随之增加；但随着用于预报的输入弧长增加，预报残差的STD并没有明显的改善趋势。表4将所有站不同预报弧段预报残差STD的均值进行了统计。可更清晰地看到，24 h预报残差STD的均值小于30 mm，6 h的预报残差STD的均值小于13 mm。但3种策略不同弧段的预报残差STD均在同一量级。

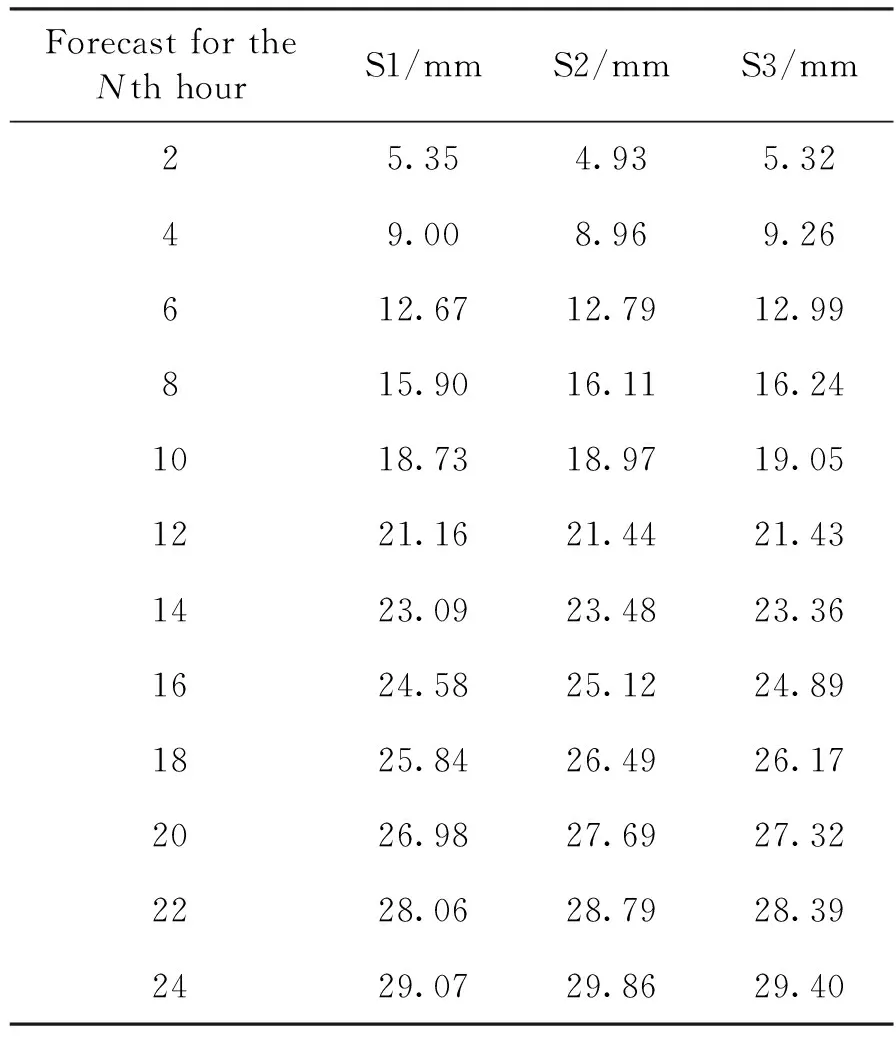
表4 九个站ZTD不同预报弧段预报残差STD的均值

5 分析与讨论

由于对流层延迟变化频繁，为了更直观地进行分析，对9个站的对流层ZTD、ZHD及ZWD进行了二次多项式拟合并绘图，拟合弧段从2018年7月1日至2019年6月30日共365 d，如图10所示。

从图10中可以看出，ZHD较为平稳且幅值较大，决定了ZTD的幅值量级，ZWD幅值比ZHD小但变化幅度较大，具有较为明显的季节性趋势，是构成ZTD波动的主要因素。除HARB和KOKB站以外，其余的ZHD幅值均约为2.2 m，结合9个站的地理位置分布(见图2)，可以看出测站高程与ZHD幅值成反比。位于赤道附近的KOUR站的ZTD幅值虽大，但波动范围适中，其预报残差序列的均值及STD均处于中间水平。位于南极洲的OHI2站、MCM4站的ZTD幅值及波动较小，其预报残差的均值及STD均处于较好水平。可见，预报精度与ZWD的波动密切相关。

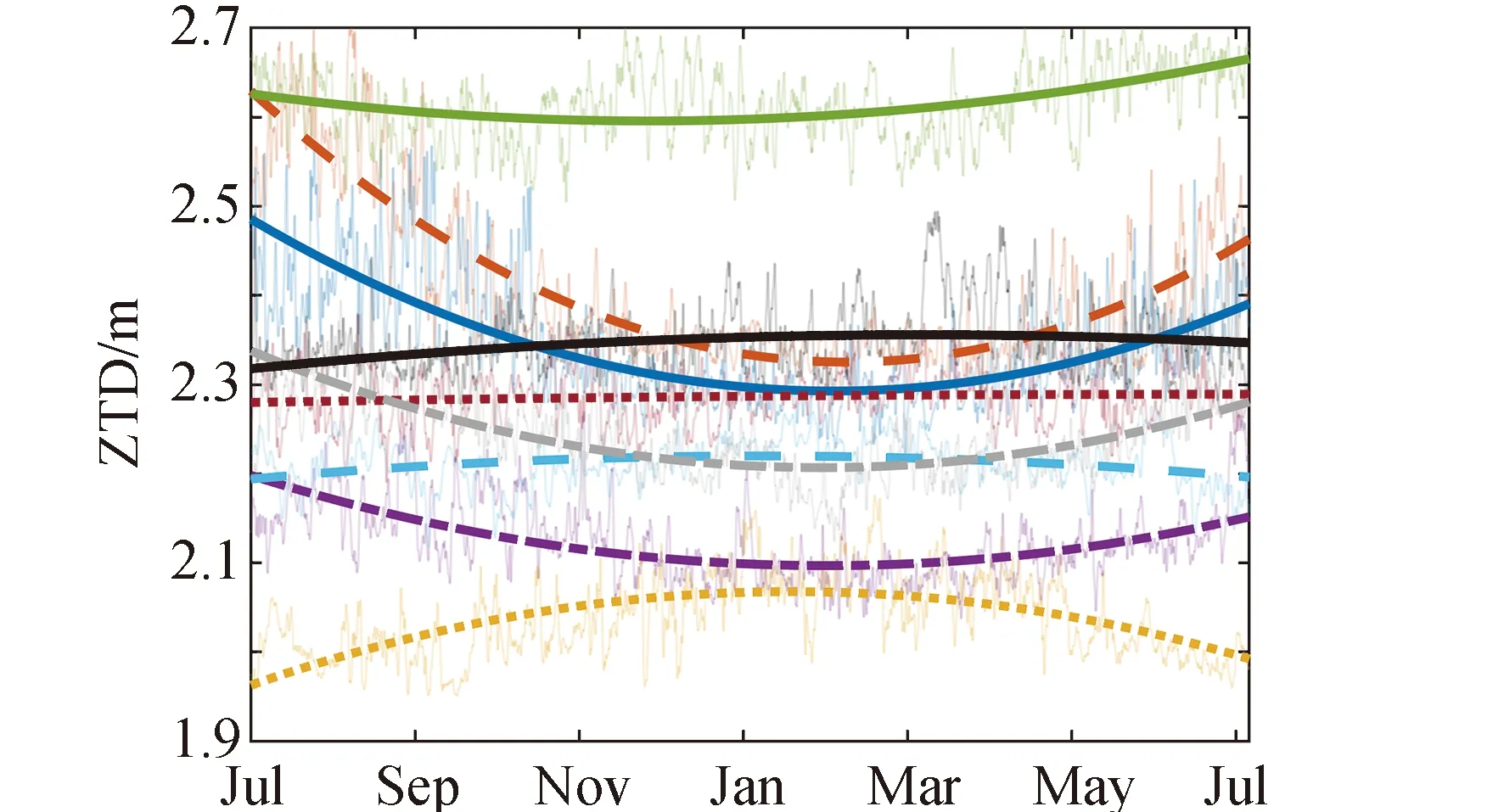
图10 2018年7月至2019年6月9个IGS跟踪站的对流层的平滑曲线ZTD，ZHD，ZWDFig.10 Smoothed tropospheric ZTD, ZHD and ZWD of 9 IGS tracking stations from Jul. 2018 to Jun. 2019

随着输入步长的增加，预报残差的均值均呈降低趋势。但3种策略的预报残差STD均在同一量级。经观察，该量级与ZWD的变化范围有关。对使用策略S1的9个站的不同弧段ZTD预报残差的STD求均值，然后对9个站的STD均值和其各自对应的ZWD变化范围求相关性系数。如图11所示，预报残差的STD与ZWD变化范围的相关性系数为0.85。作为影响ZTD波动的主要因素，ZWD变化频繁、较难捕捉规律，导致其仍是限制ZTD预报精度的主要原因。而预报残差所对应的是数据中未能进行有效建模的部分，因此预报残差STD与ZWD变化范围具有强相关。结合图2中的地理分布及图10中的ZWD幅值，可以看出ZWD幅值与纬度强相关，并且赤道与极地范围内的ZWD变化范围较小。因此，在后续的模型改进中，可考虑将纬度作为重要因素引入模型。

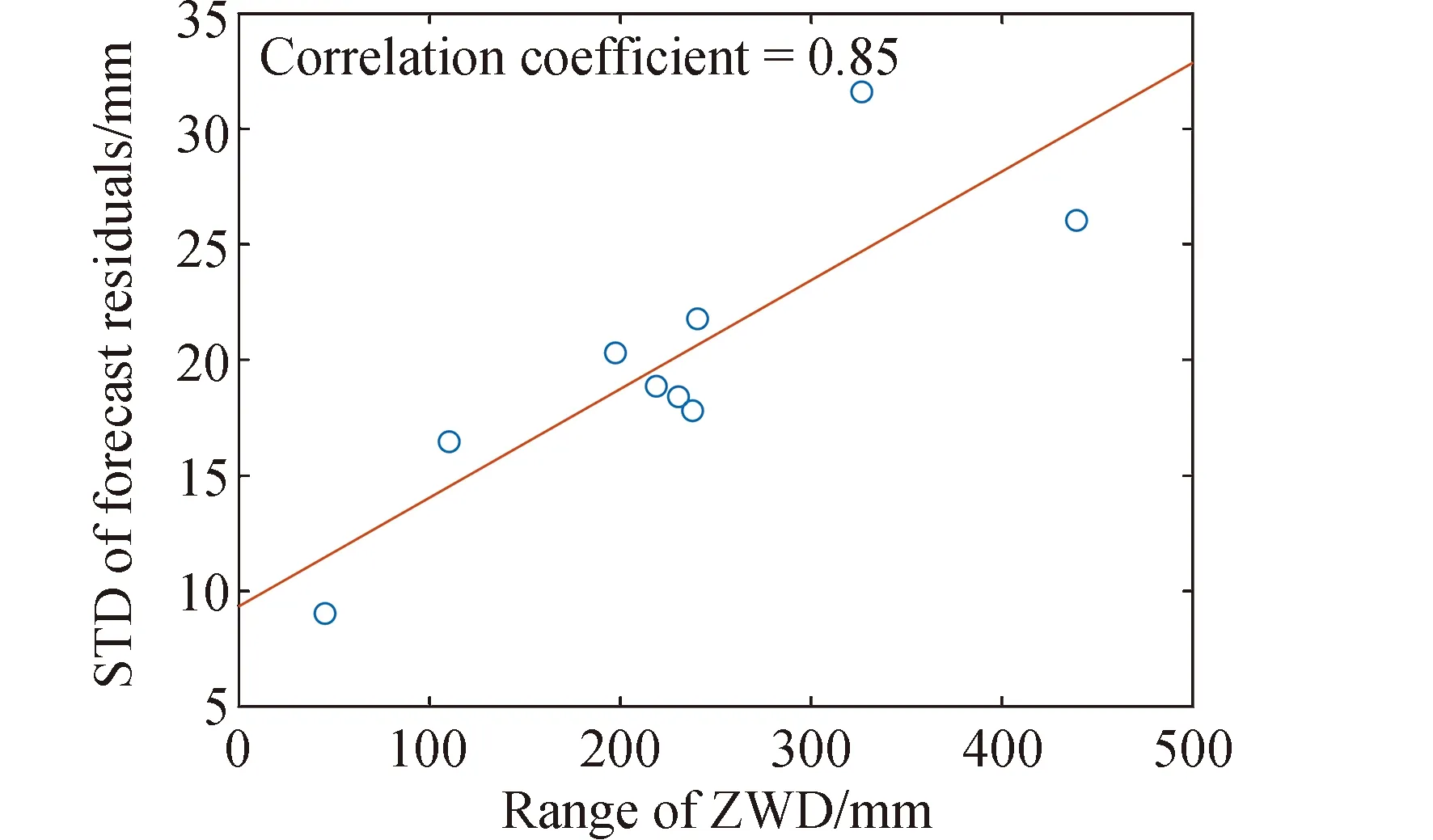
图11 九个站ZWD与预报残差STD的相关性示意Fig.11 Correlation between ZWD and standard deviation of forecast residuals of 9 stations

6 结论

基于N-BEATS数据驱动算法，设计了3种对流层ZTD预报策略，用于预报的输入数据弧长分别为24 h、48 h和72 h。选取了9个分布均匀的IGS跟踪站进行研究，数据弧段从2002年1月1日到2019年6月30日共计18.5 a，选取前17.5 a来训练模型，最后一年用来进行精度评估验证。

首先对N-BEATS算法的重复性进行了评估。从BJFS站3种策略的9组预报残差结果来看，该算法具有良好的重复性。

然后对N-BEATS算法的不同弧段预报精度进行了评估。统计结果表明，ZTD的波动范围决定预报残差的均值及STD。12 h以内预报残差的均值大多在亚毫米量级。随着预报弧长的增加，残差均值的精度逐渐衰减。但随着用于预报的输入弧长的增加，残差均值的精度衰减可得到有效改善。预报残差STD的幅值随着预报弧长的增加，呈增大趋势，但不同策略的预报残差STD没有明显区别。经观察分析，预报残差的STD与ZWD变化范围有较强相关性，而ZWD变化范围与纬度存在相关性，因此，在未来的预报研究中将侧重于通过引入纬度因子来改善ZWD的影响。

基于N-BEATS的预报策略的12 h以内的平均预报精度可达亚毫米量级，且具有较高时间分辨率，有利于进行诸如实时精密单点定位等GNSS实时应用。

致谢：感谢中国科学院国家授时中心iGMAS 分析中心、国家科技基础条件平台-国家空间科学数据中心(http:∥www.nssdc.ac.cn)。