神奇的质心

邵勇

周末，宁宁跟着妈妈一起去参观科技馆。科技馆里各式各样的小发明让宁宁看得眼花缭乱，她只能一边感叹发明者的巧思，一边目不转睛地看着各类新奇有趣的物件。突然，角落里一个奇怪的跷跷板引起了宁宁的注意。

跟公园里的跷跷板不同的是，这个跷跷板的支点是可以随意调整的。跷跷板的旁边还竖着一个展示牌，上面写着“给我一个支点，我可以撬起整个地球”。宁宁凑到跷跷板跟前观察了很久，发现跷跷板被分成了相等的三段。旁边的工作人员看见宁宁这么感兴趣，就走上前询问：“小朋友，你想不想用跷跷板把你妈妈‘跷’起来啊？”宁宁很是疑惑：“妈妈比我重这么多，我怎么能把她‘跷’起来呢？”工作人员微微一笑：“当然可以。”

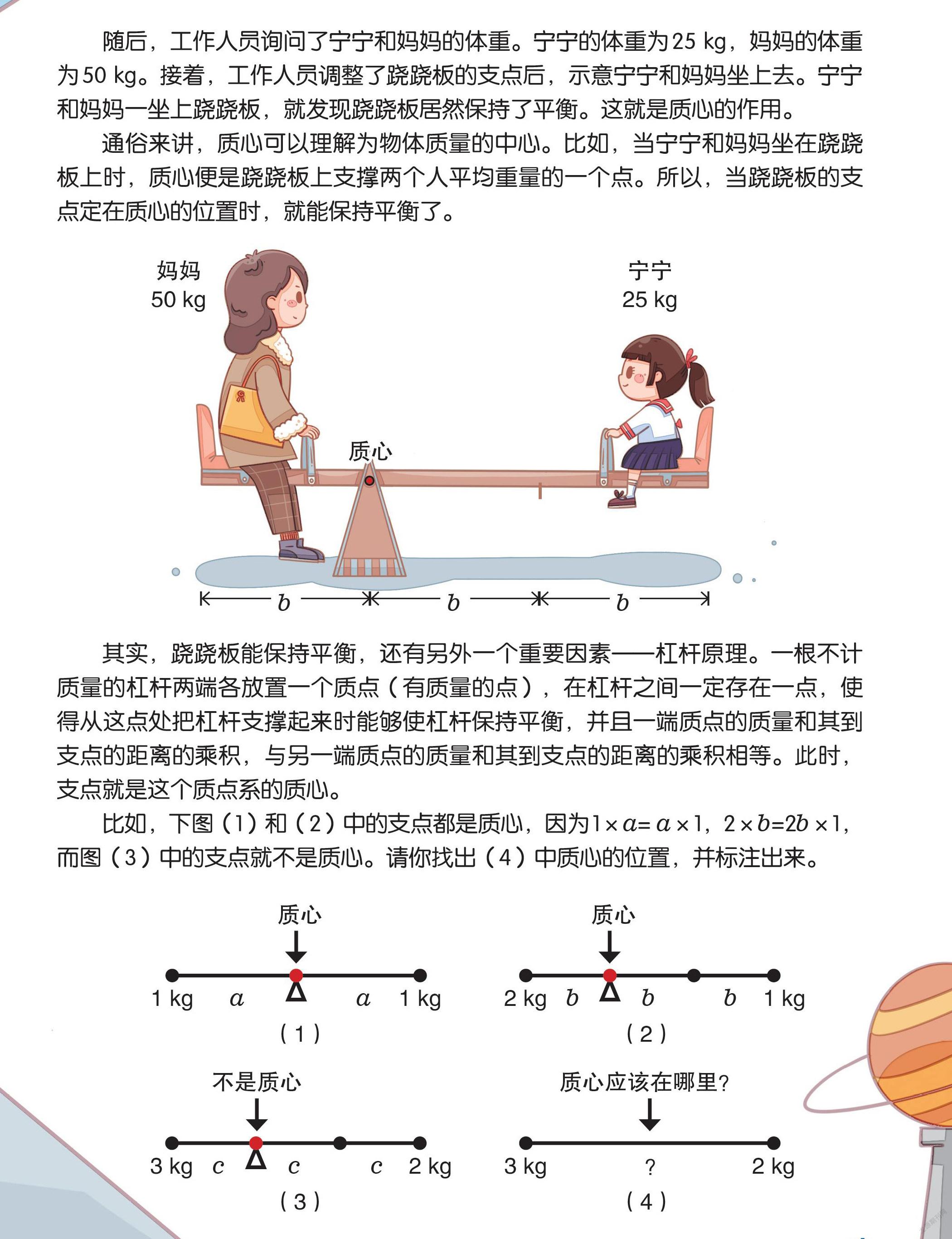
随后，工作人员询问了宁宁和妈妈的体重。宁宁的体重为25 kg，妈妈的体重为50 kg。接着，工作人员调整了跷跷板的支点后，示意宁宁和妈妈坐上去。宁宁和妈妈一坐上跷跷板，就发现跷跷板居然保持了平衡。这就是质心的作用。

通俗来讲，质心可以理解为物体质量的中心。比如，当宁宁和妈妈坐在跷跷板上时，质心便是跷跷板上支撑两个人平均重量的一个点。所以，当跷跷板的支点定在质心的位置时，就能保持平衡了。

其实，跷跷板能保持平衡，还有另外一个重要因素——杠杆原理。一根不计质量的杠杆两端各放置一个质点（有质量的点），在杠杆之间一定存在一点，使得从这点处把杠杆支撑起来时能够使杠杆保持平衡，并且一端质点的质量和其到支点的距离的乘积，与另一端质点的质量和其到支点的距离的乘积相等。此时，支点就是这个质点系的质心。

比如，下图（1）和（2）中的支点都是质心，因为1×a= a×1，2×b=2b×1，

而图（3）中的支点就不是质心。请你找出（4）中质心的位置，并标注出来。

梦中的宝藏

很久很久以前，有这么一个人，他住在罗曼。某日，累得筋疲力尽的他在花园中的无花果树下睡着了。他梦见有一个人来到他面前，对他说他的好运在罗兰。第二天，他便上路去罗兰。

到达罗兰时，天色已晚，于是他就在一个寺庙外露宿。半夜时分，人们把他当作打劫的强盗，打了一顿之后就送他去了警察局。刑警队长问他：“你是谁？从哪里来？”他说：“我从罗曼来。有人托梦说我的好运在这里，我就来了。没承想，好运还不知在哪里呢，却先挨了这么一顿暴打。命苦啊！”说着，他便痛哭起来。

刑警队长听了，反而哈哈大笑起来，对这个罗曼人说：“真是可笑，只是梦中人说你在这里有好运，你就来了。曾经我还三次梦到过在罗曼有一所大宅子，宅子后面有一个花园，花园中有一棵无花果树，树后面有一个喷泉，喷泉下面埋着宝藏。但是，我才不信这些乱七八糟的怪梦呢。你赶紧拿了这几块钱，回家去吧。”

罗曼人回到家，突然发现罗兰刑警队长梦中所见与他家的花园非常相似。他恍然大悟，马上冲到花园喷泉旁挖了起来。他果真挖到一个盒子，打开后，里面却没有宝藏，只有一块木板。这不是一块完整的长方形木板，而是一块形状像手枪一样的木板。木板上有字迹，虽然被长久埋在地下，但字迹仍依稀可辨。

这块木板的形状与花园的形状相似，而宝藏就埋在花园的质心处。但你——也就是找到这块木板的你，一定要记住，必须精确定位质心的位置，且误差不得超出一个人的手掌范围，否则会有意外发生，后果不堪设想。

宝藏的位置

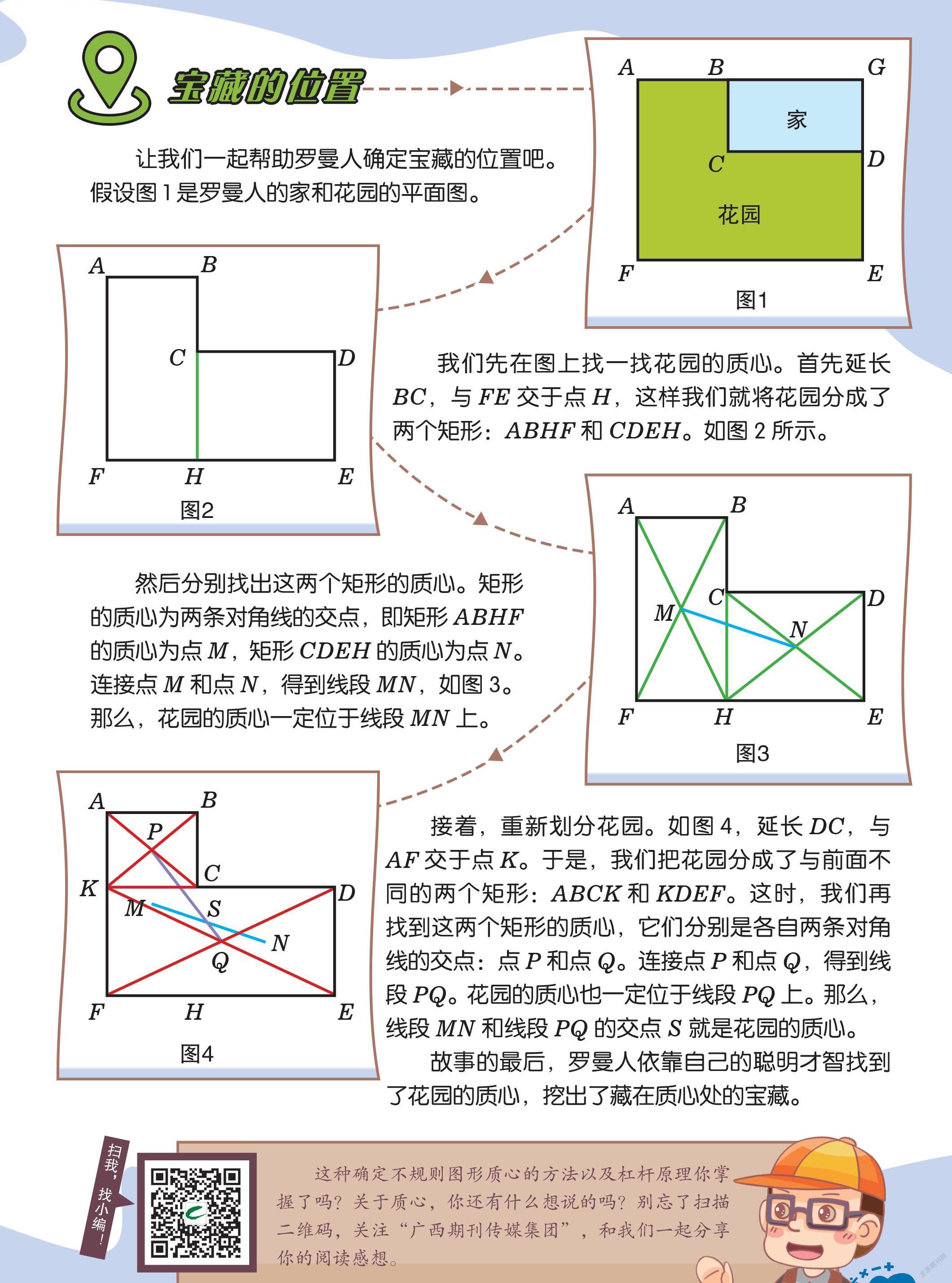
让我们一起幫助罗曼人确定宝藏的位置吧。假设图1是罗曼人的家和花园的平面图。

我们先在图上找一找花园的质心。首先延长BC，与FE交于点H，这样我们就将花园分成了两个矩形：ABHF和CDEH。如图2所示。

然后分别找出这两个矩形的质心。矩形的质心为两条对角线的交点，即矩形ABHF的质心为点M，矩形CDEH的质心为点N。连接点M和点N，得到线段MN，如图3。那么，花园的质心一定位于线段MN上。

接着，重新划分花园。如图4，延长DC，与AF交于点K。于是，我们把花园分成了与前面不同的两个矩形：ABCK和KDEF。这时，我们再找到这两个矩形的质心，它们分别是各自两条对角线的交点：点P和点Q。连接点P和点Q，得到线段PQ。花园的质心也一定位于线段PQ上。那么，线段MN和线段PQ的交点S就是花园的质心。

故事的最后，罗曼人依靠自己的聪明才智找到了花园的质心，挖出了藏在质心处的宝藏。