一般位置下凸体的截面与投影体积不等式

李爱军, 曹子昕

(河南理工大学 数学与信息科学学院, 河南 焦作 454000)

0 引言

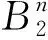
(1)

(2)

其中：u⊗u是Rn上秩为1的投影算子,In是Rn上的恒等映射。值得注意的是,John位置是由正交变换唯一确定的。显然立方体[-1,1]n和半径为1的正则单纯形均在John位置。当K是对称凸体时,条件(1)显然成立。

近来,MARKESINIS[9]得到了在John位置上的中心对称凸体的任意k-维截面的体积至多为(4n/k)k/2。随后,ALONSO-GUTIÉRREZ等[4]证明了凸体在更多情况的体积估计,例如:k-维仿射子空间和最小表面积位置。

本文目的是应用BALL[3,12]和BARTHE[5]提出的思想,并使用了Brascamp-Lieb不等式的几何版本以及它的逆不等式(引理1)。建立比John位置更一般的位置上,中心对称凸体的k-维截面及其极体投影的体积不等式。

1 预备知识

本节给出凸几何的一些基本定义和符号[13-14]。Rn表示n-维欧式空间(n≥2)，记‖·‖为Rn中的范数。

对于任意的x∈Rn,Rn中内点非空的紧凸集称为凸体，凸体K的支撑函数h(K,·):Rn→R定义为:

h(K,x)=max{〈x,y〉:y∈K}，

其中〈x,y〉是x和y的标准内积。

如果原点是凸体K的内点,那么K的极体K°定义为:

K°={x∈Rn:〈x,y〉≤1,对于所有y∈K}。

由极体定义可以立即得到:如果K1、K2是包含原点为内点的两个凸体,那么对于任意x∈Rn,有

K1⊆K2⟹h(K1,x)≤h(K2,x),

(3)

(4)

若F是Rn中的一个子空间,由文献[13],则有

(K∩F)°=PFK°。

(5)

设K是包含原点为内点的凸体,那么凸体K的Minkowski泛函‖·‖K定义为:

‖x‖K=min{t>0:x∈tK},x∈Rn。

在这种情况下,

‖x‖K=h(K°,x)。

(6)

对于任意的p∈(0,∞),凸体K的体积表示为:

(7)

其中积分是关于Rn上的Lebesgue测度。

2 主要结果

首先给出Brascamp-Lieb不等式及其逆的几何形式。

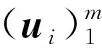
(8)

那么对于积分函数fi:R→[0,∞),i=1,…,m,有

(9)

(10)

值得一提的是,BRASCAMP等[15]第一次得到Brascamp-Lieb不等式。BALL[3]证得的不等式(9)几何形式在解决逆等周不等式中起着至关重要的作用。利用质量传输理论,BARTHE[5]给出了Brascamp-Lieb不等式一个新的证明并建立了逆Brascamp-Lieb不等式(10)。然后BARTHE使用这些不等式获得了新的逆等周不等式,也证明了BALL的逆等周不等式的等号成立的唯一性。

对等式(8)两边同时取迹，可以得到

(11)

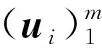
C={x∈Rn:|〈x,ui〉|≤ai,i=1,…,m},

设J={1≤i≤m:PFui≠0},其中PF是Rn中子空间F上的正交投影。

定理1 设K是Rn中的中心对称凸体且K⊆C,那么,对于Rn中k-维子空间F,有

其中δi=ci‖PFui‖2。

证明设J={1≤i≤m:PFui≠0}。对于任意的x∈F,由等式(2),可以得到

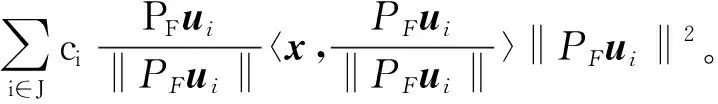
设

则有

(12)

其中IF表示F上的恒等映射。明显地,对任意的i∈J,vi是单位向量,对等式(12)两边同时取迹,则有

(13)

首先,证明不等式

对于任意的i∈J,可以得到

K∩F⊆C∩F=

{x∈F:|〈x,ui〉|≤ai,1≤i≤m}=

{x∈F:|〈x,PFui〉|≤ai,1≤i≤m}=

{x∈F:|〈x,vi‖PFui‖〉|≤ai,i∈J}=

{x∈F:|〈x,vi〉|≤hi,i∈J},

其中

因此,根据等式(12),并应用Brascamp-Lieb不等式的几何形式(9)和等式(13),得到

|K∩F|≤|C∩F|=

其中χA(·)表示集合A的特征函数。

由几何算术平均不等式和等式(11),有

(14)

进而可以得到不等式

其次,证明不等式

对于对称凸体C={x∈Rn:|〈x,ui〉|≤ai,1≤i≤m},可以立即推出

其中conv表示集合的凸包。

根据式(4)和式(5),有

(K∩F)°⊇(C∩F)°=PFC°=

其中J={1≤i≤m:PFui≠0}。

因此,对于任意的x∈F,由不等式(3)和等式(6),得到

h(K∩F,x)≤h(C∩F,x)=

‖x‖(C∩F)°=

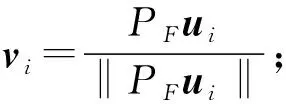
对任意的i∈J,定义:

fi(t)=exp(-|t|hi),t∈R。

根据等式(7)和式(12),并在F上使用逆Brascamp-Lieb不等式(10)、等式(13)和不等式(14),得到

k!|(K∩F)°|≥k!|(C∩F)°|=

所以

证毕。

注意到,当ai=1(i=1,…,m)时,定理1已被MARKESINIS[9]和ALONSO-GUTIÉRREZ等[4]证明。

3 结束语

通过对John位置上凸体的任意k-维截面的体积的分析,利用Brascamp-Lieb不等式的几何版本及其逆不等式,解决了一般位置下中心对称凸体的k-维截面及其极体投影的体积不等式问题,为估计一般位置下凸体的k-维截面及其极体投影的体积不等式提供了可以借鉴的思路。后续有望对一般位置下凸体的k-维截面体积不等式进行深入研究,得到更一般的凸体截面不等式。