ΦS,F-调和映射的稳定性
2022-04-19韩英波薛玉莹韩晓园
韩英波,薛玉莹,王 艳,韩晓园
(信阳师范学院 数学与统计学院, 河南 信阳 464000)
0 引言
设(Mm,g)和(Nn,h)是紧致无边的黎曼流形,u:M→N是光滑映射,u的能量定义为

的解, 那么称u是调和映射。
NAKAUCHI[1]引入泛函
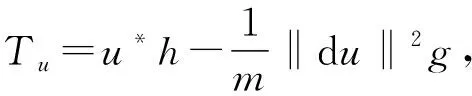
的临界点, 那么称u为F-调和映射。
韩英波等[5]引入泛函
得到泛函ΦF(u)的第一、第二变分公式, 并证明了从球面Sm(m≥4)出发或到达球面Sn(n≥4)的F-稳态映射是弱共形的。

divS=-〈τ(u),du〉。
为了研究S=0成立的条件, 韩英波[7]引入泛函
其中dvg是M上的体积元。 在局部正交标架场{ei}下, 应力-能量张量的范数为

文献[9-11]定义了Φ-能量密度、Φ-能量、Φ-调和映射及稳定Φ-调和映射, 得到Φ-能量泛函的第二变分公式, 找到一些Φ-超强不稳定(Φ-SSU)流形, 并证明了每个紧致的(Φ-SSU)流形一定是Φ-强不稳定(Φ-SU)流形。
1 预备知识
引入一个新的能量泛函:
其中dvg是(M,g)上的体积元, ‖Su‖表示应力-能量张量的范数, 在局部正交标架场{ei}下,有
对Mm(m≥5) 上任一向量场X, 取M上的一个局部正交标架场 {ei}, 定义张量σu如下:
设映射F:[0,∞)→[0,∞), 且有F(0)=0,F′(t)>0, 那么u的F-张量场τF(u) 为
定义1 若u是Euler-Lagrange方程τF(u)=0的解, 则光滑映射u称为泛函ΦS,F(u)的ΦS,F-调和映射。
设u:(M,g)→(N,h) 是光滑映射, 对M上任意的向量场X、Y, 泛函ΦS,F的2阶对称张量SF称为SF-应力能量张量, 且
2 ΦS,F-调和映射的第一变分公式


(1)
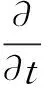

其中利用等式
设Xt是M上的紧支集变分向量场, 使得对M上的任意向量场Y有

则
(2)
由式(2)和Green’s公式, 可得
证毕。
命题1 设u:(M,g)→(N,h)是光滑映射,SF是F-应力能量张量, 对M上任意向量场X, 有
(divSF)(X)=-h(τF(u),du(X))。
证明在p∈M点附近取局部正交标架场{ei}使得∇eiej|p=0。 设X是M上的向量场,在p点处有
h(σu(ei),(∇eidu)(X)]-h(τF(u),du(X))。
由于(∇Xdu)(ei)=(∇eidu)(X),所以
(divSF)(X)=-h(τF(u),du(X))。
证毕。
由命题1可知, 如果u:(M,g)→(N,h)是ΦS,F-调和映射, 那么
divSF=0,
(3)
即u满足ΦS,F-守恒律。
对于2-阶张量T1、T2∈Γ(T*M⊗T*M), 设{ei}是度量g下的一组正交基, 定义内积如下:
(4)
对任意X∈Γ(TM),Y∈Γ(TM), 对于1-形式θX(Y)=g(X,Y), 2-阶张量场∇θX为:
(∇θX)(Y,Z)=g(∇YX,Z)。
(5)
引理1[6]设X为张量场,T是(0,2)型张量场, 对于X方向上度量g的李导数LX, 有
(6)
事实上, 在正交标架场{ei}上, 有


定理2(第一变分公式(II)) 设u:(M,g)→(N,h)是光滑映射, 对于李导数LX, 取M上的局部正交标架场{ei}, 则有
证明根据定理1, 由ut=u°φt易得ut的变分向量场du(X), 因此
(7)
取局部正交标架场{ei}, 在点p有
h(du(∇eiX),σu(ei))]=
(8)
由式(7)和式(8),可得

证毕。
3 第二变分公式



其中RN是N的曲率张量。

(9)



(10)
式(10)右边第一项为
B1+B2,
(11)
式(11)右边第二项为

(12)
对于M上任意向量场Y, 设X1、X2、X3、X4和X5是M上的紧支集变分向量场, 使得
式(11)右边第一项为


(13)
当s=0,t=0时, 式(13)为
B1=div(X1)+div(X2)+div(X3)+
根据Green’s公式, 上式积分为0, 结合式(10)~式(13), 即得结论。证毕。

4 从球面Sm出发的ΦS,F-调和映射
定理4 设Sm(m≥5)是m维球面,N是黎曼流形,u:Sm→N是ΦS,F-调和映射, 假设
则u是不稳定的。
证明在p∈Sm附近取局部正交标架场{ei}, 使得∇eiej|p=0, 再选定em+1使得{ei,em+1}是Rm+1上的正交标架场。 在Rm+1上取一个固定正交基EA(A=1,…,m+1), 设
(14)
其中〈·,·〉表示标准欧式内积, 则du(VA)∈Γ(U-1TN)且
(15)
(16)
(17)
由条件
以及式(15), 得
(18)
对于M的任意光滑向量场X, 根据Weitzenböck公式, 有
du(RicSm(X))=(Δdu)(X)+
(∇2du)(X),
(19)




I1+I2+I3+I4+I5+I6+I7。
(20)
在p点的局部正交基{ei}下分别计算I1、I2、I3、I4、I5、I6及I7,其中对任意的i,j=1,…,m, 有∇eiej|p=0。
(21)
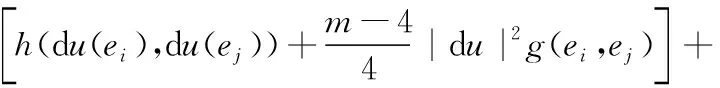
(22)
(23)
h((∇ekdu)(ei),du(ej))×
h(du(ei),(∇ekdu)(ej))],
(24)
h((∇ekdu)(ej),du(ej)),
(25)
(26)
d((∇ekdu)(ei),du(ej))-
d((∇ekdu)(ej),du(ei))-
h((∇ekdu)(ej),du(ej))。
(27)

5 到达球面Sn的ΦS,F-调和映射
定理5 设M是m-维紧致黎曼流形,Sn(n≥5)是n-维标准球,u:Mm→Sn是ΦS,F-调和映射, 若
则u是不稳定的。
证明取p∈SN附近的局部正交标架场{ei,…,en}, 且满足∇eiej|p=0, 取en+1使得{en,en+1}是Rn+1上的正交标架场。 在Rn+1上取一个固定正交基EA(A=1,…,n+1), 设
(28)

[h(du(εα),du(εβ))+


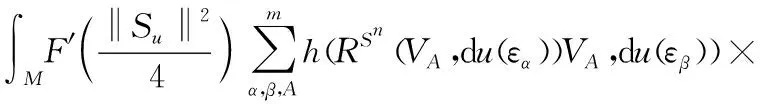
J1+J2+J3+J4+J5+J6。
(29)
在p点处,计算
(30)
通过式(28)和式(30),可得下列结果:
(31)
类似于J1的推导过程,可得
(32)
(33)
(34)
(35)

h(du(εα),σu(εα))h(ei,ei)]=
(36)
结合式(31)~式(36), 可得
(39)
因此u是不稳定的。 证毕。
6 结语
首先引入ΦS,F-调和映射的能量泛函, 然后结合SF应力能量张量, 计算得到ΦS,F-调和映射的第二变分公式, 并证明了在一定条件下,从球面Sm(m≥5)出发的或到达球面Sn(n≥5)的ΦS,F-调和映射是不稳定的映射。
