基于勒让德多项式的MMC自适应反步控制策略

2022-04-19徐雷夏向阳敬华兵刘奕玹贺烨丹易海淦

中国电力 2022年3期

徐雷，夏向阳，敬华兵，刘奕玹，贺烨丹，易海淦

(1. 长沙理工大学电气与信息工程学院，湖南长沙 410114；2. 株洲中车机电科技有限公司，湖南株洲 412005)

0 引言

模块化多电平换流器（modular multilevel converter, MMC）作为新一代的电压源型换流器因为其模块化设计、拓展性强、有效冗余、最小化无源滤波器尺寸和谐波水平低等优点[1-4]，近年来在新能源并网、STATCOM、高压直流输电、变速电机驱动器和储能系统等领域中得到广泛关注[5-10]。与常规电压源型换流器不同，MMC系统中拥有众多控制变量，动态方程中又表现出非线性的特征，常规使用的线性控制器没有考虑桥臂电流、子模块电容电压等动态特性带来的影响，这使得线性控制器无法兼顾稳定性和响应速度之间的平衡，控制器参数难以整定[11-12]。

目前已有文献采用不同方法针对MMC的非线性特征对系统所带来的不利影响进行了相关研究。文献[13-14]采用滑模控制，但该控制方法的颤振问题没有得到解决，容易损坏电力电子器件。文献[15-16]采用模型预测控制，该控制方法基于目标函数最优的目标，避免了控制器参数整定，可实现对多个系统变量的控制，但需要精确的MMC模型。文献[17-18]采用反馈线性化方法，使所得到的闭环系统成为线性化，但非线性抵消的问题无法解决。

反步控制法（back-stepping control,BSC）将Lyapunov函数的选择与控制器的设计相结合，是一种具有不确定系统综合方法的系统控制器，已在多领域应用[19-21]，可以提供出色的瞬态性能，以满足系统对快速响应能力的要求。

反步控制法在电力电子换流器中的应用也是目前的研究重点。文献[22]采用反步控制法在三相静止坐标系下建立了空间动态模型，从而无需锁相环，但在高度复杂的动态系统中效果不佳。文献[23]针对升压换流器建构了四阶非线性状态空间模型，采用反步控制方法用于内环矫正功率因数，但控制目标具有局限性。文献[24]采用自适应反步法对MMC进行控制，但该方法直接加入自适应变量进入反步控制系统，导致计算量过大，并且使用回路过多，难以实现。上述方法都没有考虑系统内部参数的不确定性，由于信号大干扰、操作环境和温度的变化等因素的影响，电路中的元件参数会产生不确定性的变化，而这些变化在工程应用中是要有所考虑的。加装滤波电容、嵌入温度平衡算法等方法的适用性是有限的，外接电容所带来的电压传感器同样会有噪声干扰，额外的控制回路会增加整个系统的计算压力, 并且无法完全修正变化参数。在非线性模型中，若不对动态模型进行补偿修正，必然影响动态模型的准确性，从而影响系统的安全运行。

本文提出一种基于勒让德多项式的MMC反步控制策略，可对输出电流和子模块电容电压进行追踪控制。另外，在MMC动态模型中引入勒让德多项式来估计不确定性变化，补偿由于参数变化所带来的误差。MMC系统的实验结果也证明了所提控制策略的优越性。

1 MMC拓扑结构及静止坐标系下的动态模型

1.1 MMC系统拓扑结构

MMC的拓扑结构如图1所示，其中，Vdc为直流侧电压；R0和Rt分别为桥臂等效电阻和交流侧等效电阻；L0和Lt为桥臂等效电感和交流侧等效电感；ipj和inj（j=a,b,c）分别为j相的上桥臂和下桥臂电流；upj和unj分别为j相的上桥臂和下桥臂电压；ij为交流侧输出相电流；uj为交流侧输出相电压。在正常情况下，子模块的输出电压为0或者电容电压，这取决于IGBT的工作状态。

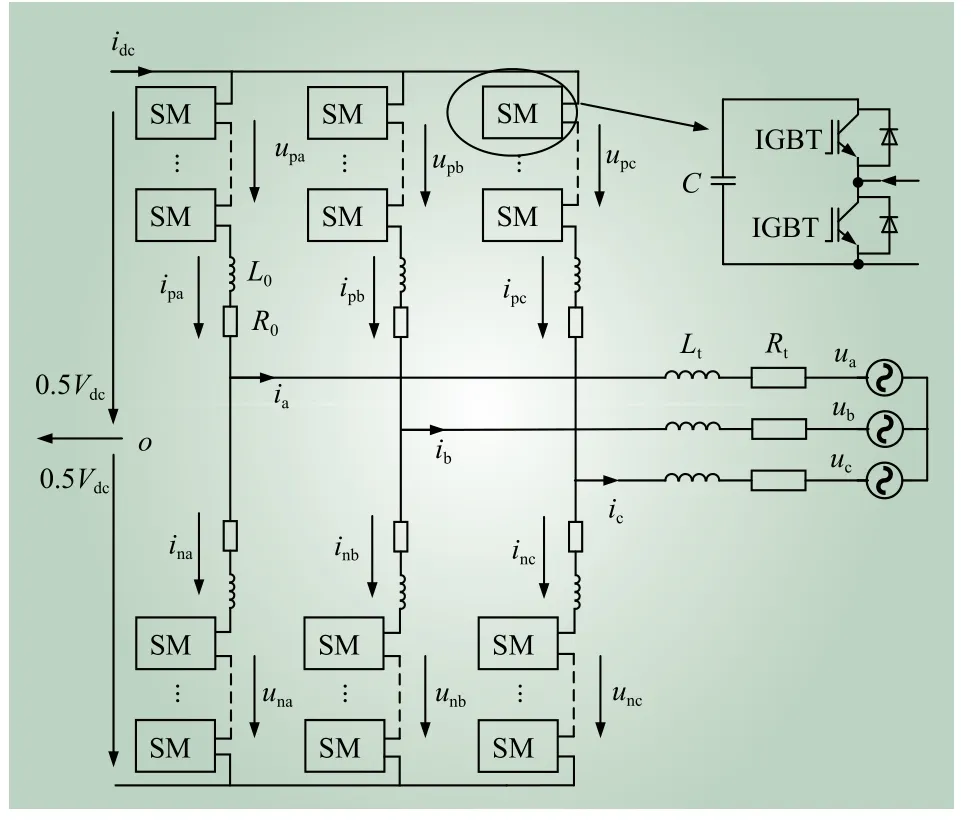
图1 MMC拓扑结构Fig. 1 Topologic structure of MMC

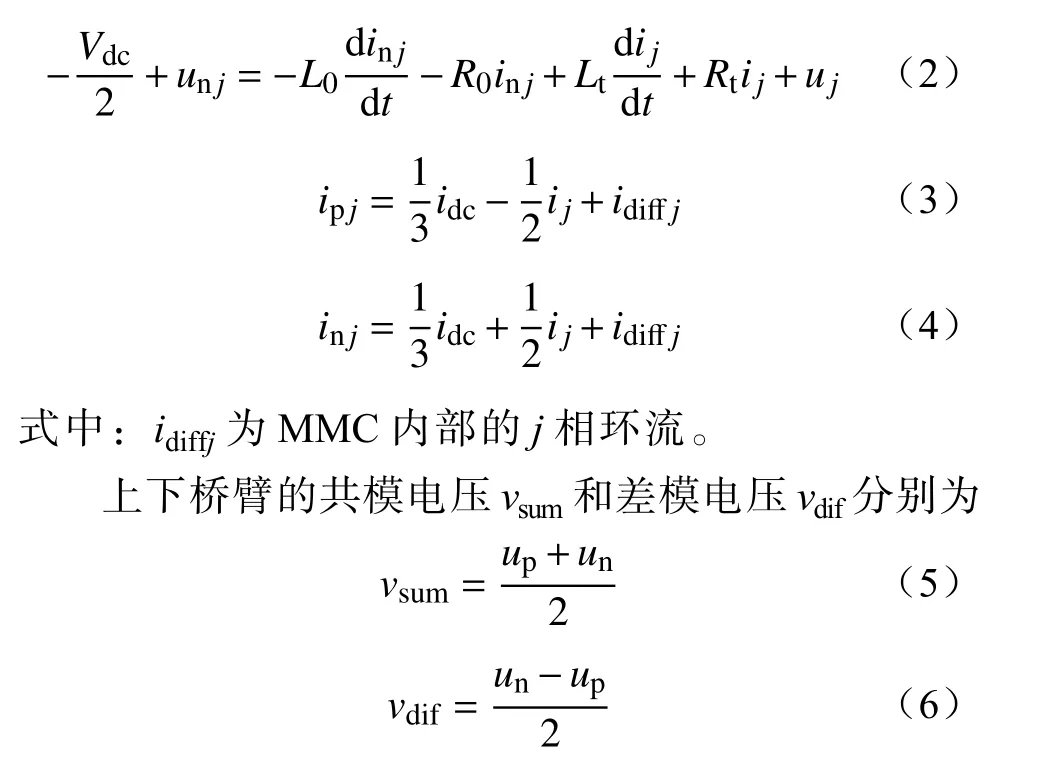
1.2 MMC静止坐标系下的动态模型

由式（10）可知，桥臂输入能量对时间的导数中存在桥臂电流ip_n（j），桥臂电流可作为桥臂输入能量的调控参数，进而桥臂输入能量、桥臂电流和桥臂电容电压之和作为状态变量构成一个反步控制系统，其结构原理如图2所示。

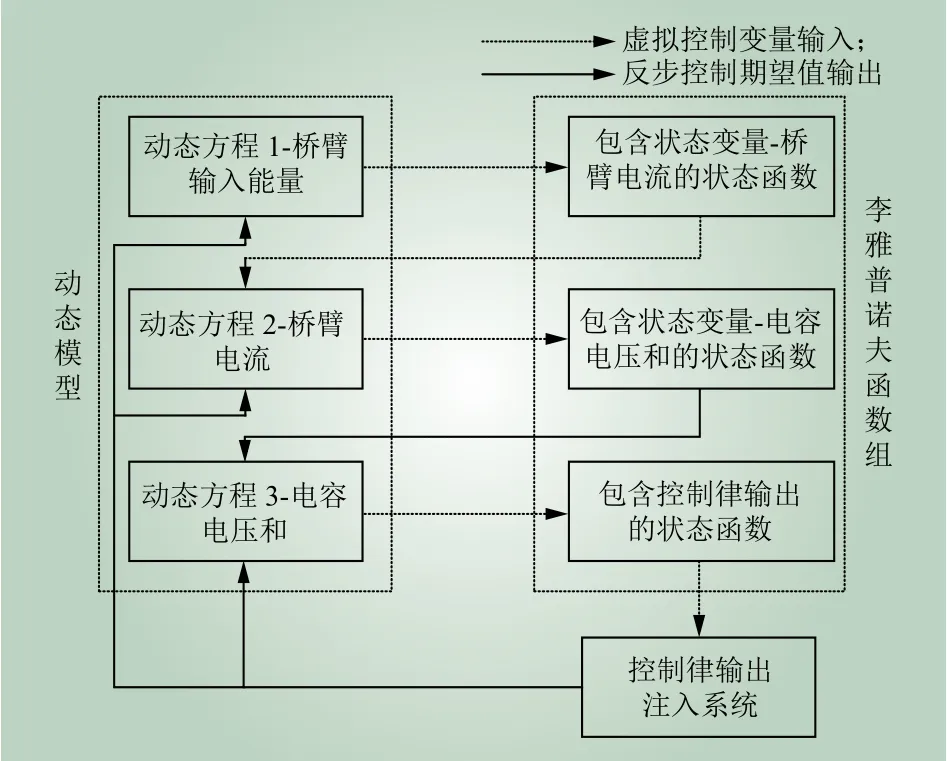
图2 反步控制系统原理Fig. 2 Schematic diagram of back-stepping control system

2 基于勒让德多项式的自适应反步法控制器设计

首先，根据状态变量和误差函数建立Lyapunov函数组，由Lyapunov稳定性定理求得正常工况下的控制率输出。然后，针对系统参数变化，在状态变量中加入自适应变量，并引入勒让德多项式进行逼近跟踪，求得更新后的控制率输出。最后，通过Barbalat引理验证控制器效果。

2.1 设计步骤1

2.2 设计步骤2

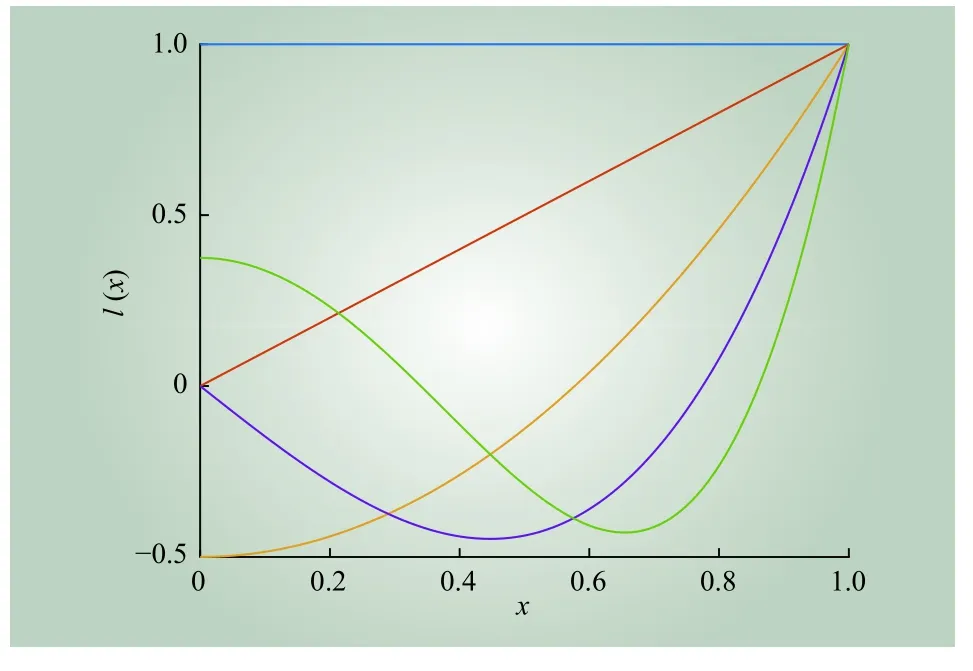
图3 勒让德多项式前5项示意Fig. 3 Schematic diagram of the first 5 terms of Legendre polynomial

图4 本文所提控制策略的总控制框图Fig. 4 The overall control block diagram of the proposed control strategy

3 仿真测试与实验验证

通过PSCAD仿真软件搭建三相MMC仿真模型，对本文所提出的新型稳定控制策略的有效性进行验证，并与PI控制器进行对比分析。仿真参数如表1所示。

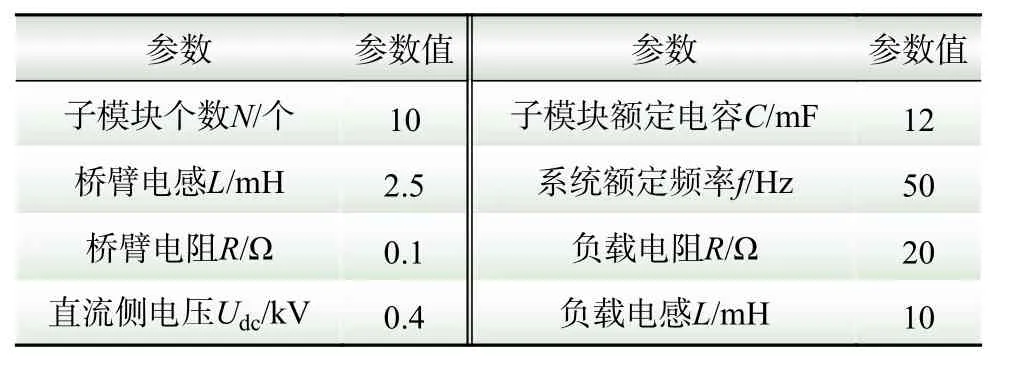
表1 仿真系统参数Table 1 Simulation system parameters

3.1 负载突变下暂态性能测试

当系统工况发生改变或者系统内部发生故障时会对MMC内部参数产生影响，该扰动可以体现在负载参数发生变化上，这使得实际负载的参数会偏移理论值，导致动态模型精准性下降，影响系统的暂态性能和控制能力。设置直流电压为0.4 kV，0.5 s时有功负载突变，图5给出了有功负载突变情况下2种控制方法的对比仿真结果。

图5 有功阶跃时2种控制方法的对比仿真结果Fig. 5 Comparative simulation results of two control methods during active power step

对比图5a)、b)可以发现，2种方法的输出电流和输出电压值都能维持三相电流电压对称且被控制在合理范围内，但本文所提控制中的输出电流在0.5 s后拥有更小的过冲值。由图5c)可以看出本文所提控制中的桥臂环流幅值更小，被良好抑制在限定区域内；而PI控制器控制的循环电流幅值较大，高频次分量较多。由图5d)可以发现，以0.5 s为基准，自适应反步控制下达到稳定峰值的时间为t1=0.019 32；PI控制下达到稳定峰值的时间为t2=0.037 30，这说明本文所提控制器的控制精准度更高，暂态性能更好。

通过图5e)可以说明，2种方法都能抑制电容电压之和的改变，但本文所提控制器的误差相对更小。PI控制器在应对非线性特征明显的MMC系统时，稳态和瞬态误差较大，而本文所提出的控制策略利用勒让德多项式的无模型化的逼近特性和自适应反步法的稳定性，有效降低了瞬态误差，在面对有功负载突变的情况下具有更好的控制能力。

类似的，设置直流电压为0.4 kV，0.5 s时无功负载突变。无功负载突变情况下2种控制方法的对比仿真结果如图6所示。当无功功率发生阶跃变化时，采用本文所提控制方法得到的输出电流过冲仍小于PI控制方法下输出电流过冲；并且循环电流的控制效果也优于PI控制方法。自适应反步控制法的无功功率阶跃峰值时间为t3=0.013 85，PI控制下的无功功率阶跃峰值时间为t4=0.031 97；自适应反步控制的电容电压误差小于PI控制下的电容电压误差。图6的结论与图5的结论类似，进一步验证了基于勒让德多项式的自适应反步控制的显著优越性。

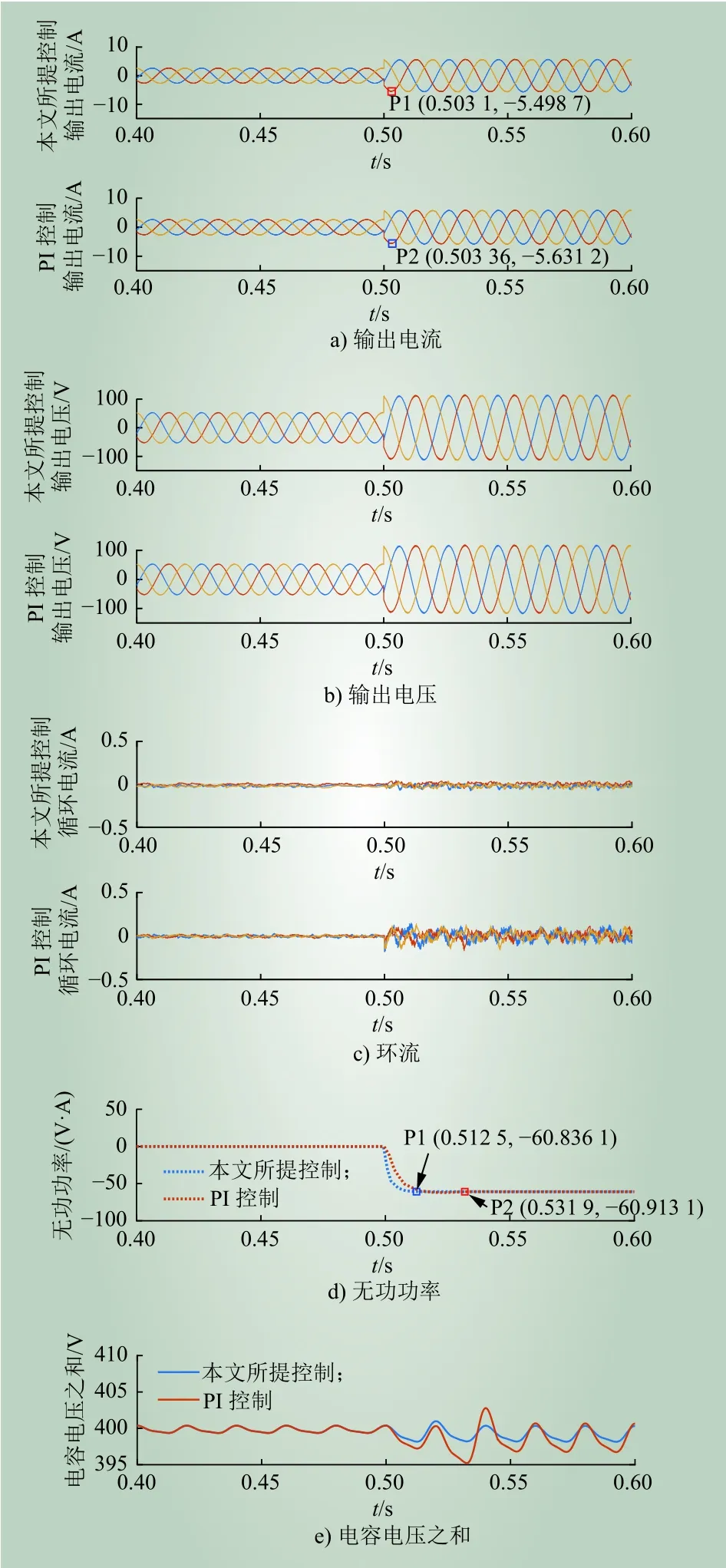
图6 无功阶跃时两种控制方法的对比仿真结果Fig. 6 Comparative simulation results of two control methods during reactive power step

为验证勒让德多项式的逼近效果，设用于估计自适应变量勒让德系数初始值为0，自适应学习率y为0.08，勒让德系数估计值如图7所示。观察图7可以发现，在0.5 s时负载突变，估计值全部趋于稳定且最后收敛于某一常数，实现了对不确定误差的逼近。

图7 勒让德系数估计值Fig. 7 Legendre coefficient estimate

3.2 鲁棒性能测试

当MMC系统桥臂内部的电路参数发生变化时，探究自适应反步控制器在不同桥臂电路参数运行条件下的鲁棒性能。假设系统在0.5 s时发生负载突变，其输出电流波形如图5a）所示，现在给定桥臂电阻和桥臂电感的取值范围0.05≤R0≤0.15（Ω）,1≤L0≤4（mH），图8和图9给出了桥臂不同参数下输出电流的变化趋势。

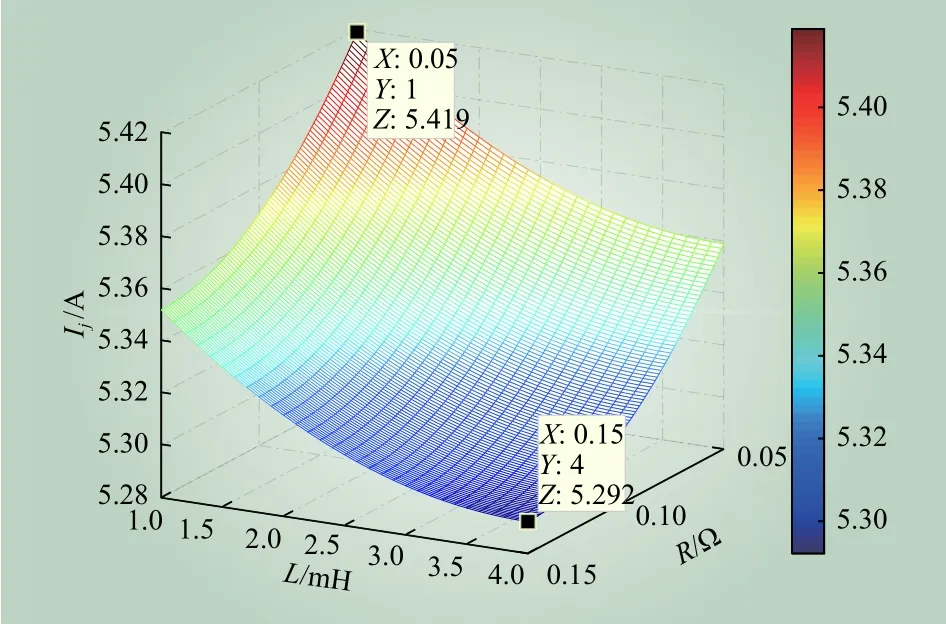
图8 桥臂不同参数下输出电流峰值变化趋势Fig. 8 Change trend of output current peak value under different parameters of bridge arm

图9 桥臂不同参数下的输出电流曲线Fig. 9 Output current curve under different parameters of bridge arm

根据图8可知，在给出的参数浮动范围内，输出电流的最大变化率控制在2.34%，其变化曲面较为平缓，对MMC输出电流的影响较小。由图9可知，在2种极端情况的MMC参数下，对0.5 s负载突变后的输出电流产生了微弱的影响，其改变仍在可控范围内。由上述结果可以说明，本文所提出的控制方法对控制目标的跟踪能力优越，即使是在内部参数改变的情况下，依旧能控制暂态和稳态误差在合理范围内，抵御电路参数改变所带来的负面影响，保证优越的控制性能。

3.3 实验验证

实验样机外观如图10所示，实验平台主电路参数如表2所示。实验结果如图11所示。

表2 实验系统参数Table 2 Experimental system parameters

图10 实验样机照片Fig. 10 Experimental prototype photos

图11 负载突变下的实验结果Fig. 11 Experimental results under load mutation

图11中，ib为b相的输出电流；idiffj（j=a,b,c）分别为a、b、c三相桥臂环流；idc（b）为桥臂电流直流分量；vCu（b）为b相桥臂电容电压之和。由图11可知，本文所提控制策略能有效控制负载突变情况下的输出电流过冲，使其稳定在合理范围内。由三相环流的实验波形可以确认，基于勒让德多项式的反步控制器能显著控制负载突变下的环流幅值，环流幅值有效降低26%，并且满足10%的可控最大阈值。本文所提控制策略能有效消除桥臂电流中直流分量的脉动，降低负载变化情况下对系统功率传输的影响。

在图11d)中，t1时刻前，系统处于正常运行状态；t1时刻后，负载突变，采用传统控制方法；t2时刻后，改用新型稳定控制方法。由图11d)可以看出，本文所提控制策略与传统控制策略都能将桥臂电容电压和稳定在合理范围内，但本文所提的稳定控制策略无论是在稳态还是暂态下都能拥有更小的误差值。由上述实验结果可以验证所提出的基于勒让德多项式的MMC自适应反步稳定控制策略的可行性和理论分析的有效性。