基于SAE-DBN的联合收割机液压系统运行状态监测

2022-04-19姜洪远杨光友刘威宏

液压与气动 2022年4期

姜洪远，杨光友,2，刘浪, 刘威宏

(1.湖北工业大学农机工程研究设计院，湖北武汉 430068； 2.湖北省农机装备智能化工程技术研究中心, 湖北武汉 430068)

引言

目前，国内外的各种类型联合收割机已广泛应用液压控制技术。液压系统的应用使收割机机械结构整体布置更紧凑、质量更轻，操作更方便，更易于实现自动控制[1]。由于联合收割机作业环境恶劣且粉尘较多，为保障联合收割机的正常运行，对联合收割机液压系统的监测显得尤为重要[2-3]。国内外学者进行了广泛的研究；何丽平[4]将模糊系统和神经网络相结合，建立模糊神经网络的数学模型，构造了基于模糊神经网络的联合收割机液压故障诊断系统；陈章位[5]研究了信号时域-频域分析处理的小波分析，提出了机械系统状态特征提取的新途径，并将其应用于电液伺服系统状态监测中，实现了系统状态特征的定量描述；周汝胜等[6]团队提出了基于模糊化规则的FARX模型，并将此模型应用于挖掘机液压系统之中；张若青等[7]采用多步预测神经网络对多级液压伺服系统进行故障诊断，并通过仿真和实验验证了多步预测神经网络对多级液压伺服系统进行故障诊断的有效性；SEPASI M,SASSANI F[8]设计了应用无迹卡尔曼滤波器对液压系统进行在线故障诊断系统；MOZAFFARI A等[9]提出了一种用于具有分组方法、数据处理和基于语法仿生监督的可进化自组织神经模糊多层分类器的液压系统故障诊断方法。

基于液压系统非线性特点，本研究提出了一种将SAE和DBN融合的联合收割机液压系统运行状态监测系统，该系统先使用SAE直接对由传感器输入的原始信号进行特征提取，然后通过DBN进行二次特征提取，建立联合收割机液压系统状态参数和状态类型之间的非线性映射，摆脱了对人工经验诊断的依赖，提高了对联合收割液压系统工作状态监测的准确率和实时性，为液压系统故障诊断打下基础。

1 SAE-DBN模型的建立

1.1 堆叠自动编码器

由Rumelhart等提出的自动编码器与其他前馈神经网络类似，都是由输入层、隐藏层和输出层组成，如图1所示。自动编码器的输出层和输入层具有相同的神经元个数，且隐藏层的神经元个数小于输入层和输出层。通过最小化输入层和输出层之间的重构误差，使得自动编码器学习到原始数据的特征表示。

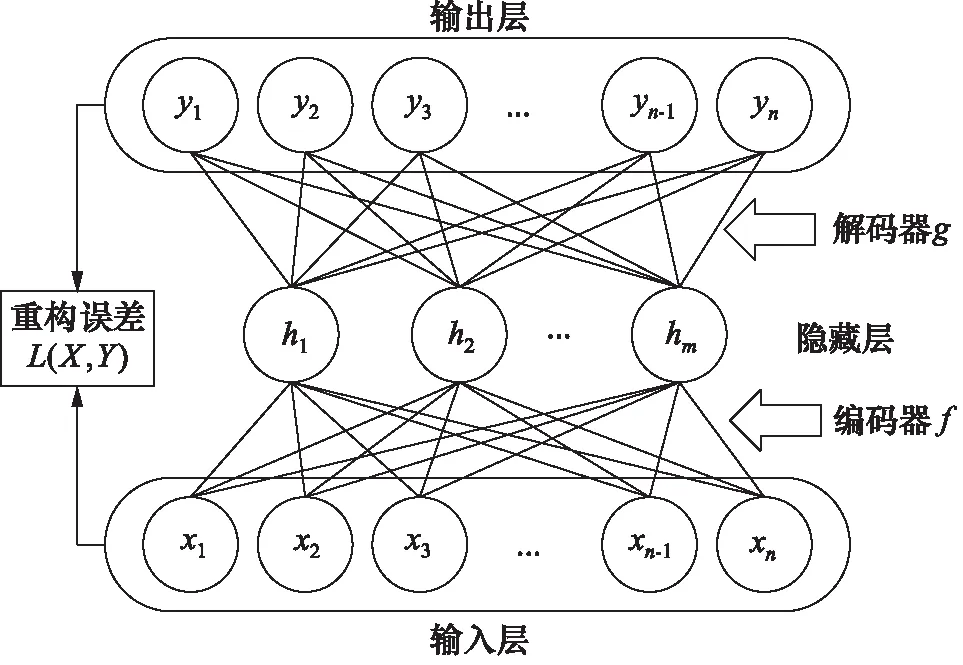
图1 自动编码器网络结构Fig.1 Autoencoder network structure

编码器是将原始数据映射到数据的隐含表示，如式(1)所示；解码器尽可能的将隐含表示重构为原始输入数据，如式(2)所示。将编码器的输出h作为原始数据的特征表示，而解码器的输出主要用于训练过程中的重构误差的计算，通过重构误差反向传播以调整神经网络的权值和偏置值。

编码器f通过式(1)将输入层的数据X=[x1,x2,…,xn]映射到隐藏层，得到原始数据的特征表示h：

(1)

其中,sf为编码器非线性激活sigmoid函数，Wij为输入层第i个神经元与隐藏层第j个神经元之间的连接权值，bj为编码器偏置值，hj为隐藏层第j个神经元的输出值，n为输入层的神经元个数。解码器g通过式(2)将原始数据的特征表示h映射到输出层，得到原始数据的重构数据Y：

(2)

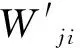
输入层的值X和输出层的值Y之间的误差为重构误差，其计算公式如式(3)所示：

(3)

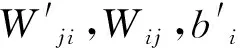
BENGIO Y等[10]在Rumelhart等提出的自动编码器(AE)的基础上提出的堆叠自动编码器(SAE)，能够逐层的学习原始数据更加抽象和更加复杂的特征表示。SAE是在贪婪逐层非监督预训练之后经过有监督的微调得到的，其由多个自动编码器堆叠而成，如图2所示。堆叠自动编码器的每个自动编码器以上一层自动编码器的隐藏层输出h作为输入层的输入，从而使得SAE能够获得原始输入数据更深层次的特征表示。经过无监督预训练得到的自动编码器的编码器f都将被保存，并在有监督的微调过程中作为编码器的初始权重和偏置值[11-12]。

图2 堆叠自编码器预训练原理图Fig.2 Stack Autoencoder pretraining schematic

使用自动编码器的方法训练AE1层，使用AE1层的隐藏层的值H训练AE2层，得到H的特征表示G。同理训练AE3层，直到所有AE层训练完成。将所有训练好的自动编码器的编码器依次连接，得到预训练好的SAE模型[13]。预训练好的SAE顶层加入Softmax分类器，用于对SAE的有监督微调，其网络结构如图3所示。

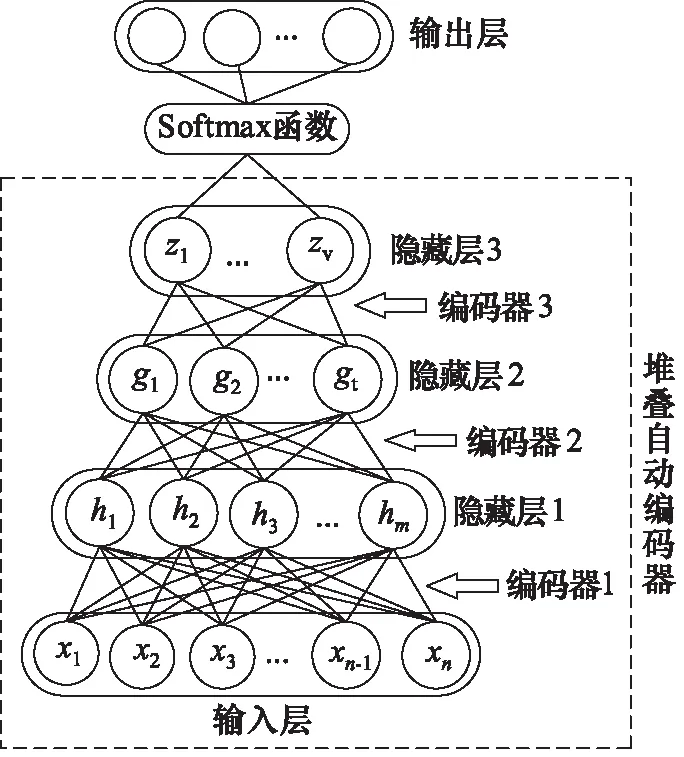
图3 堆叠自动编码器网络结构Fig.3 Stack autoencoder network structure

将预训练过程中所得到的所有编码器的权值和偏置值作为有监督微调的初始值。Softmax函数用于分类，其输出神经元个数和分类数相同。Softmax分类层的各个神经元的输出由式(4)和式(5)计算得出：

li=WiZ+bi

(4)

(5)

式中，σi(l)为第i个Softmax神经元的输出，表示该样本属于第i个类别的概率；r为类别数；Z为SAE求得的样本深层特征表示；zb为Z的第b个元素；Wi为SAE的最后一个隐藏层所有神经元到第i个Softmax神经元的权值矢量；bi为偏置值。Softmax分类函数的损失函数使用式(6)所示的交叉熵函数进行度量：

(6)

式中,yi为该样本经过one-hot编码后的标签；L为Softmax分类函数的损失函数。

1.2 深度信念神经网络

深度信念神经网络(Deep Belief Network，DBN)由Geoffrey Hinton[14]教授在2006年提出，是一种由多层非线性变量连接组成的概率生成模型[15]。DBN通过建立观察数据和标签之间的联合概率分布，对P(Observation|Label)和P(Label|Observation)均作了评估，其学习能力非常强大,可以在原始样本数据中提取有效的低维特征,以便于进行准确分类。DBN的网络结构如图7所示，由图7可知DBN是由多个受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)叠加构成的。通过贪婪逐层算法[7]训练DBN网络，从最底层的RBM开始训练,从下往上边训练边保存模型参数,直到DBN网络完成训练。与其他神经网络相比较，大大提高了训练效率[16-18]。不仅解决了局部最优问题，而且此方法是无监督的。本研究使用BP神经网络对DBN进行微调优化[19]，以提高网络的分类能力，DBN的网络结构如图4所示。

(7)

图4 DBN的网络结构Fig.4 DBN network structure

DBN网络的训练包括无监督的学习和反向调优两个过程[20]。

1) 无监督的学习

利用CD-K算法(Contrastive Divergence，对比散度算法)进行权值初始化。

(1) 随机初始化权值{W，a，b}，其中W为权重向量，a是可见层的偏置向量，b为隐藏层的偏置向量，随机初始化为较小的数值。

(2) 将X赋给显层v(0)，计算使隐层神经元被开启的概率：

(8)

其中，式中的上标用于区别不同的向量，下标用于区别同一向量中的不同维。

(3) 根据计算的概率分布进行一步Gibbs抽样，对隐藏层中的每个单元从{0,1}中抽取得到相应的值，即h(0)～p(h(0)|v(0))。详细过程如下：

首先，产生一个[0,1]上的随机数rj，然后由式(9)确定hj的值如下：

(9)

(4) 用h(0)重构显层，需先计算概率密度，再进行Gibbs抽样：

对于贝叶斯可见层神经元[21]

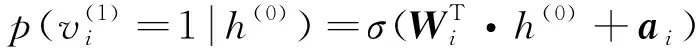
(10)

对于高斯可见层神经元

(11)

其中，N表示为正态分布函数。

(5) 根据计算到的概率分布，再一次进行一步Gibbs采样，对显层中的神经元从{0,1}中抽取相应的值来进行采样重构，详细过程如下：

首先，产生[0,1]上的随机数，然后确定vj的值：

(12)

(6) 再次用显元(重构后的)，计算出隐层神经元被开启的概率：

对于高斯或者伯努利可见层神经元

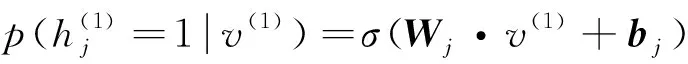
(13)

(7) 按照式(14)～式(16)更新得到新的权重和偏置。

W←W+λ[p(h(0)=1|v(0))v(0)T-

p(h(1)=1|v(1))v(1)T]

(14)

b←b+λ[p(h(0)=1|v(0))-p(h(1)=1|v(1))

(15)

a←a+λ[v(0)-v(1)]

(16)

其中，λ为学习率。

2) 反向调优

进行有监督的调优训练时，需要先利用前向传播算法，从输入得到相应的输出值，然后再利用后向传播算法来更新网络的权重值和偏置值。

(1) 前向传播

利用CD算法预训练好的W，b来确定相应隐元的开启和关闭。逐层向上传播，一层层地将隐藏层中每个隐元的激励值计算出来并用sigmoid函数完成标准化，如下所示：

(17)

最后由式(18)和式(19)计算出输出层的激励值和输出：

h(l)=W(l)·h(l-1)+b(l)

(18)

(19)

(2) 反向传播

采用最小均方误差准则的反向误差传播算法来更新整个网络的参数，则代价函数如式(20)：

(20)

其中，E为DNN学习的平均平方误差，Xi表示理想的输出，i为样本索引。(Wl,bl)表示有待学习的权重和偏置的参数。

采用梯度下降法，来更新网络的权重和偏置参数，如(21)所示：

(21)

其中，λ为学习效率。

1.3 SAE-DBN算法原理

SAE作为特征提取的一类模型，能够提取出良好的数据特征。如果将SAE提取出的特征进行二次特征提取，会产生更好的分类效果。因此本研究将SAE和DBN结合得到SAE-DBN模型。其模型结构图如图5所示。底层为SAE层，提取输入数据的深层次特征；DBN层对输入数据的深层次特征进行降维操作，得到的数据作为Softmax层的输入，Softmax层对输入样本进行分类处理，得到当前样本的种类。

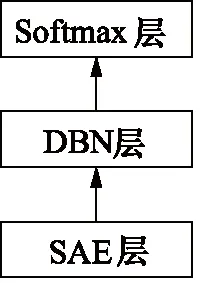
图5 SAE-DBN结构Fig.5 SAE-DBN structure

2 模型应用

为验证SAE-DBN在联合收割机液压系统运行状态监测上的有效性，于2019年5月在山东潍坊进行了联合收割机收割作业实验。采集的数据为GM80型联合收割机液压系统的压力以及相关部位的转速，而所需作物以及实验环境等信息通过人员现场测试获得。

该型号联合收割机液压系统原理示意图如图6所示，联合收割机的主要动作包括拨禾轮升降、割台升降、主离合控制、滚筒位置调节、喂入搅龙转动以及拨禾轮转动等，这些动作由拨禾轮升降油缸、割台油缸、主离合油缸、滚筒油缸、喂入搅龙液压马达和拨禾轮液压马达等执行元件来完成。该液压系统还包括换向阀、溢流阀液压锁、单向节流阀等控制元件以及液位计、冷却器、过滤器等辅助元件。

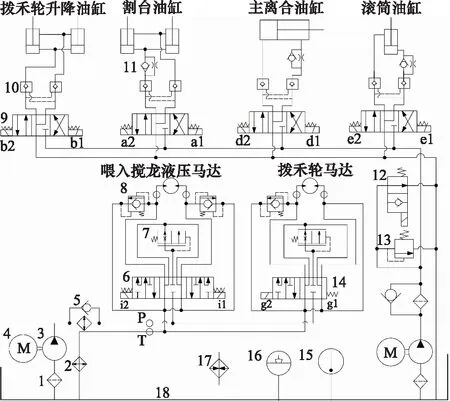
1.过滤器 2.冷却器 3.液压泵 4.电机 5.单向阀6.三位八通换向阀 7.二位二通换向阀 8.顺序阀9.三位四通换向阀 10.液压锁 11.单向节流阀12.卸荷阀 13.溢流阀 14.二位八通换向阀15.温度计 16.液位计 17.加热器 18.油箱图6 联合收割机液压系统原理示意图Fig.6 Hydraulic system schematic diagram of combine harvester

联合收割机作业时，首先接通割台油缸(a2通电)，调节割台高度，使得割台处于合适的位置；同时接通喂入搅龙液压马达和拨禾轮液压马达(i2和g2受力)，驱使喂入搅龙和拨禾轮旋转；然后接通拨禾轮升降油缸(b2通电)，油缸有杆腔进油时，油缸回缩，拨禾轮下降接触小麦。此时可驱动联合收割机进行小麦收获作业。在作业时，可接通滚筒油缸调节滚筒位置(e2通电)，以获得更优异的脱粒性能。作业结束，依次断开喂入搅龙液压马达(i2失力)、拨禾液压马达(g2失力)，接通滚筒油缸调节滚筒位置(e1通电)，回复脱离滚筒初始位置，接通割台油缸(a1通电)，调节割台高度，接通拨禾轮升降油缸(b1通电)，调节拨禾轮位置，完成联合收割机的停车作业。

实验依据国家标准GB/T 8097—2008《收获机械联合收割机试验方法》的要求，选取适当大小的试验田。由于数据采集系统存在干扰，采集到的原始数据中存在异常值和缺失值等，因此对原始数据进行预处理。若1个样本中所有属性都为0，则删除该样本；对于异常值，通过前后样本的均值取代该异常值；对于缺失值，通过样条插值法进行填补，表1为经过预处理之后的实验数据。驾驶员操作使联合收割机处于不同工作状态,采集该状态下的液压参数，如图7所示为联合收割机进行实验的实验现场图和传感器安装图。

图7 实验现场及所用传感器Fig.7 Field diagram and sensors

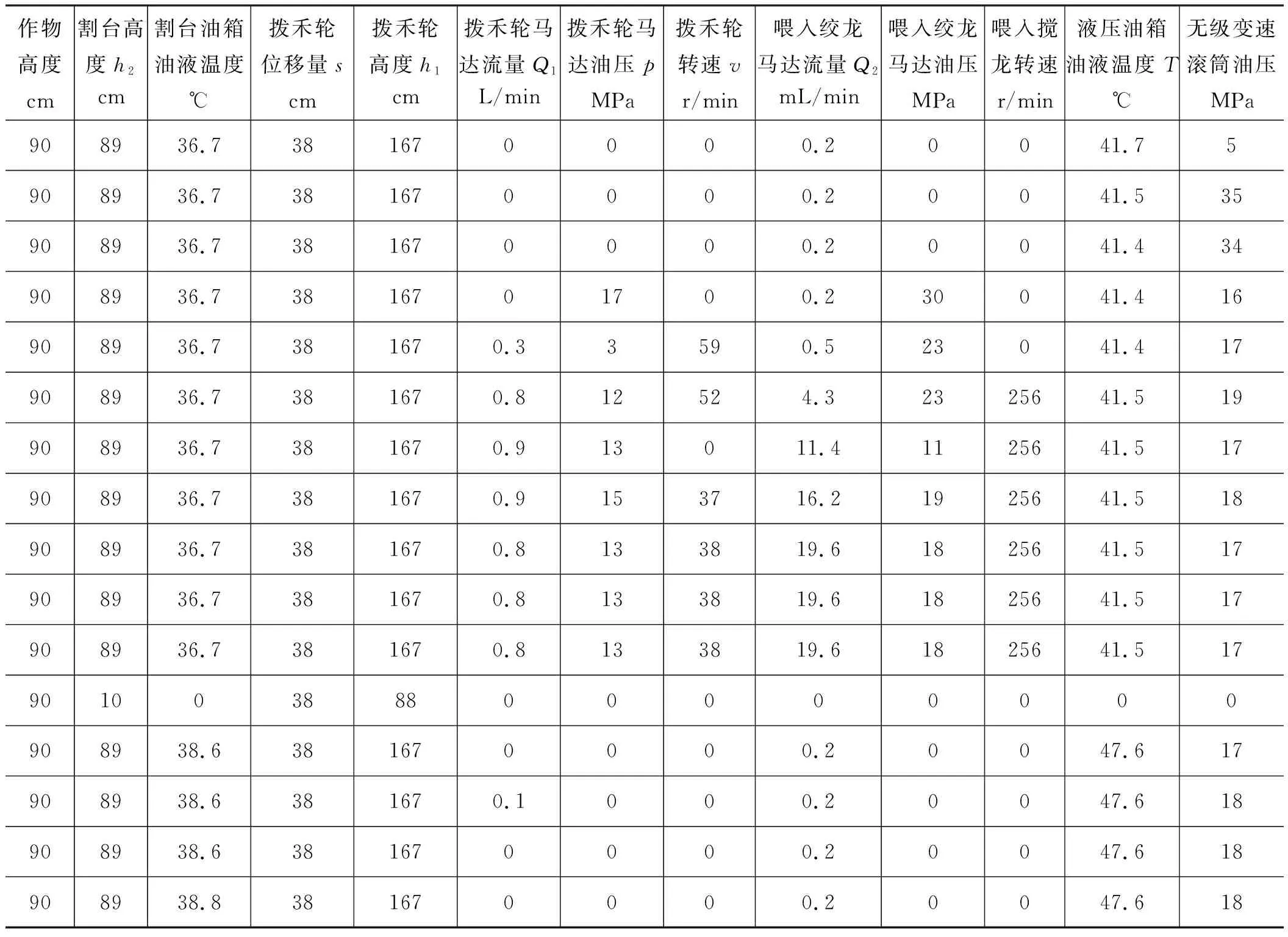
表1 主要实验数据Tab.1 Main experimental datas

实验数据经过预处理之后得到65677个样本数据，包括了联合收割机待机状态、割台低位收割短时稳定运行、割台低位收割长时稳定运行、联合收割机原地拨禾轮转动、收割时仅喂入搅龙转动、割台高位收割短时稳定运行、割台高位收割长时稳定运行、原地拨禾轮和喂入搅龙转动、喂入搅龙为高转速等九种作业状态时相应部件的液压数据。其中联合收割机处于割台低位收割短时稳定运行和割台高位收割短时稳定运行时，液压系统参数变化曲线如图8所示，作业时对应的液压系统状态One-hot编码[22]标签如表2所示。

图8 液压系统部分参数Fig.8 Partial parameters of hydraulic system

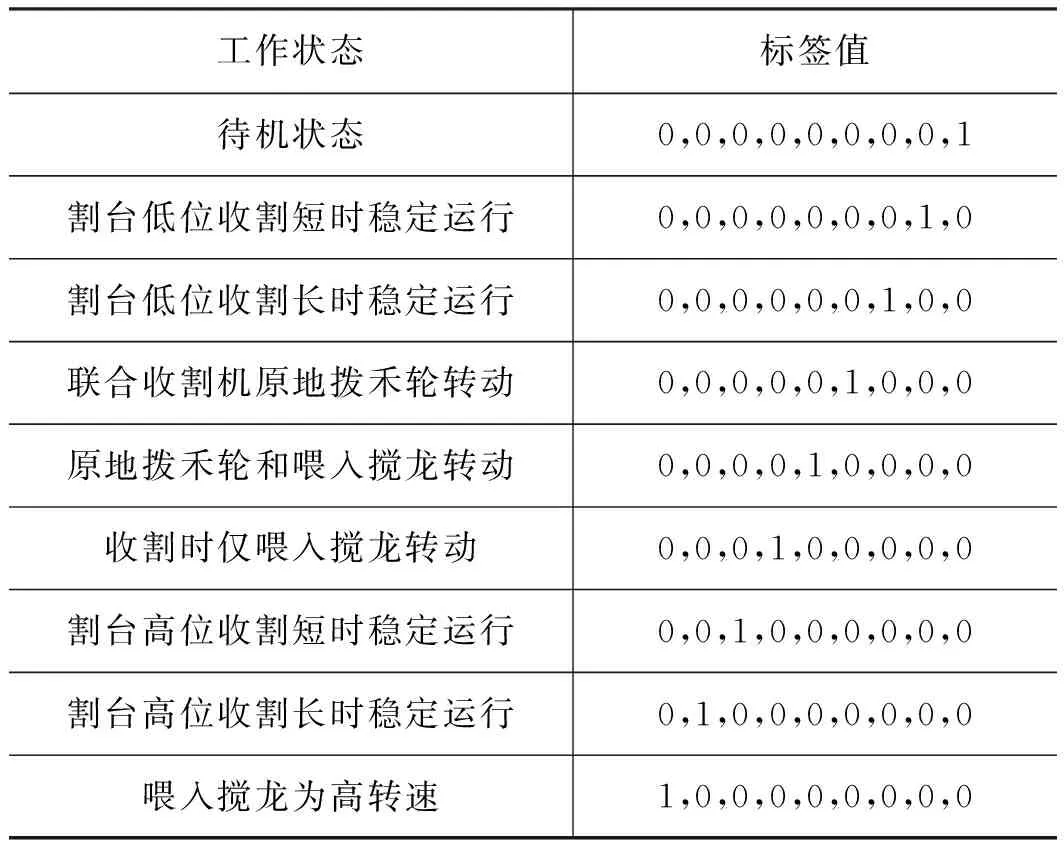
表2 液压系统工作状态对应标签Tab.2 Corresponding label of hydraulic system working state

2.1 实验有效性验证

1) 实验数据集构建和实验环境

在每个类取1000个样本数据组成测试集(9000个样本)，其余样本数据作为训练数据集(56677个样本)。实验软件环境为Windows10 64位操作系统，采用Tensorflow深度学习框架，选用Python3.5作为编程语言，硬件环境：计算机内存8GB，搭载Intel(R)Core(TM) i5-7500 CPU@3.40GHz处理器。

2) SAE-DBN模型训练

对数据进行归一化能够提升模型的收敛速度、运行速度以及模型的精度[23]，因此在模型训练之前首先用Min-Max标准化方法对数据集进行归一化处理，使得结果落在[0,1]区间内，转换函数如下：

(22)

其中,x为样本数据，xmax为数据集中的最大值，xmin为数据集中的最小值，x*为归一化后的数据。

本研究使用的SAE-DBN模型中，SAE层拥有3个自动编码层在模型的无监督深层次特征学习训练阶段，对于每个自编码网络均使用sigmoid作为激活函数[24]。DBN层拥有3个RBM网络，通过贪婪逐层算法进行训练。最后通过Softmax分类层[25]对整个网络进行有监督的微调。

3) SAE-DBN实现过程

(1) 对样本数据集进行标准化处理后，按要求将数据集分为训练集和测试集；

(2) 建立基于SAE-DBN的联合收割机液压系统运行状态监测模型；

(3) 随机初始化SAE中的所有参数，同时使用训练集中的无标签样本对SAE进行逐层预训练；

(4) 采用训练集中的标签样本通过Softmax函数对SAE进行有监督的网络调优；

(5) 随机初始化DBN网络的参数值{W，a，b}，同时使用SAE提取的无标签特征数据通过CD算法对RBM进行逐层预训练[26]；

(6) 采用SAE提取的标签特征数据通过Softmax函数对SAE进行有监督的网络调优；

(7) 将SAE和DBN叠加，使用训练数据集中的标签样本对SAE-DBN进行整个模型的参数调优[27]，直至误差小于规定值。

4) 模型训练结果

在模型训练过程中，发现联合收割机液压系统运行状态监测的准确率与AE层数和RBM层数均有一定的关系。有训练数据集经过大量的实验，绘制出三者之间的关系，如图9所示。

图9 SAE-DBN模型准确率与RBM层和AE层数之间的关系Fig.9 Relationship among accuracy of SAE-DBN model and numbers of RBM layer and AE layer

由图9可知，随着SAE中AE层数的增加，模型的准确率呈现上升趋势，且趋势逐渐变缓；准确率随着RBM层数的增加出现上升趋势。但是当RBM层数大于5层时，SAE-DBN模型的准确开始出现下降趋势。因此确定本研究使用的SAE-DBN模型由3个AE层叠加形成的SAE和5层RBM构成的DBN组成，SAE-DBN模型的每层神经元个数如表3所示，SAE-DBN网络模型训练过程中的训练准确率如图10所示，不同层的损失变化σ曲线如图11所示。

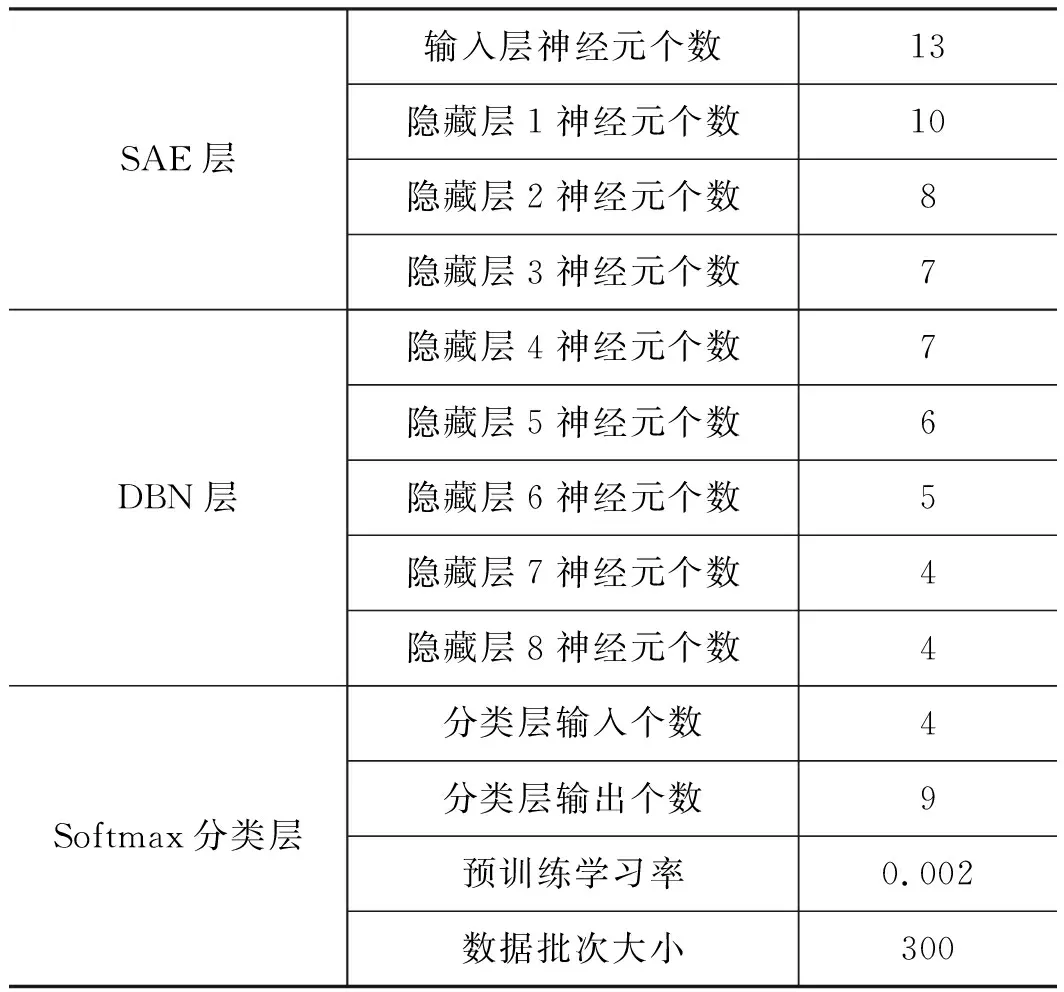
表3 SAE-DBN深度网络模型的参数设置Tab.3 Parameter setting of SAE-DBN depth network model

从图10的准确率ζ变化曲线可以看出模型的准确率随着训练次数n的增加而趋于稳定，SAE-DBN的准确率为92.47%。

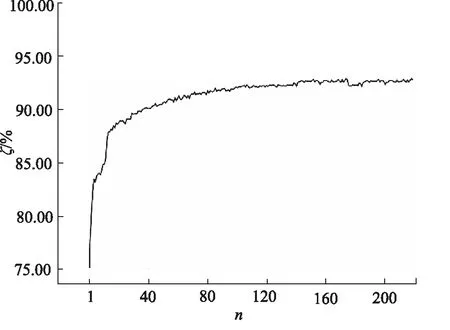
图10 SAE-DBN训练过程准确率变化曲线Fig.10 Training accuracy curve of SAE-DBN

图11 不同层的损失变化曲线Fig.11 Loss variation curves at different layers

此SAE-DBN模型在测试集上的结果如表4所示，由表4可知当操作联合收割机割台低位收割短时稳定运行、割台低位收割长时稳定运行、割台高位收割短时稳定运行、割台高位收割长时稳定运行，模型的准确率较低。本研究使用的SAE-DBN模型在联合收割机待机状态下、收割时仅喂入搅龙转动、联合收割机原地拨禾轮转动、原地拨禾轮和喂入搅龙转速同时转动等状态下有优异的性能。对基于SAE、DBN和BPNN的联合收割机液压系统运行状态监测方法，采用与SAE-DBN同样的训练集进行训练，4种模型在不同收割机状态下的性能如图12所示。

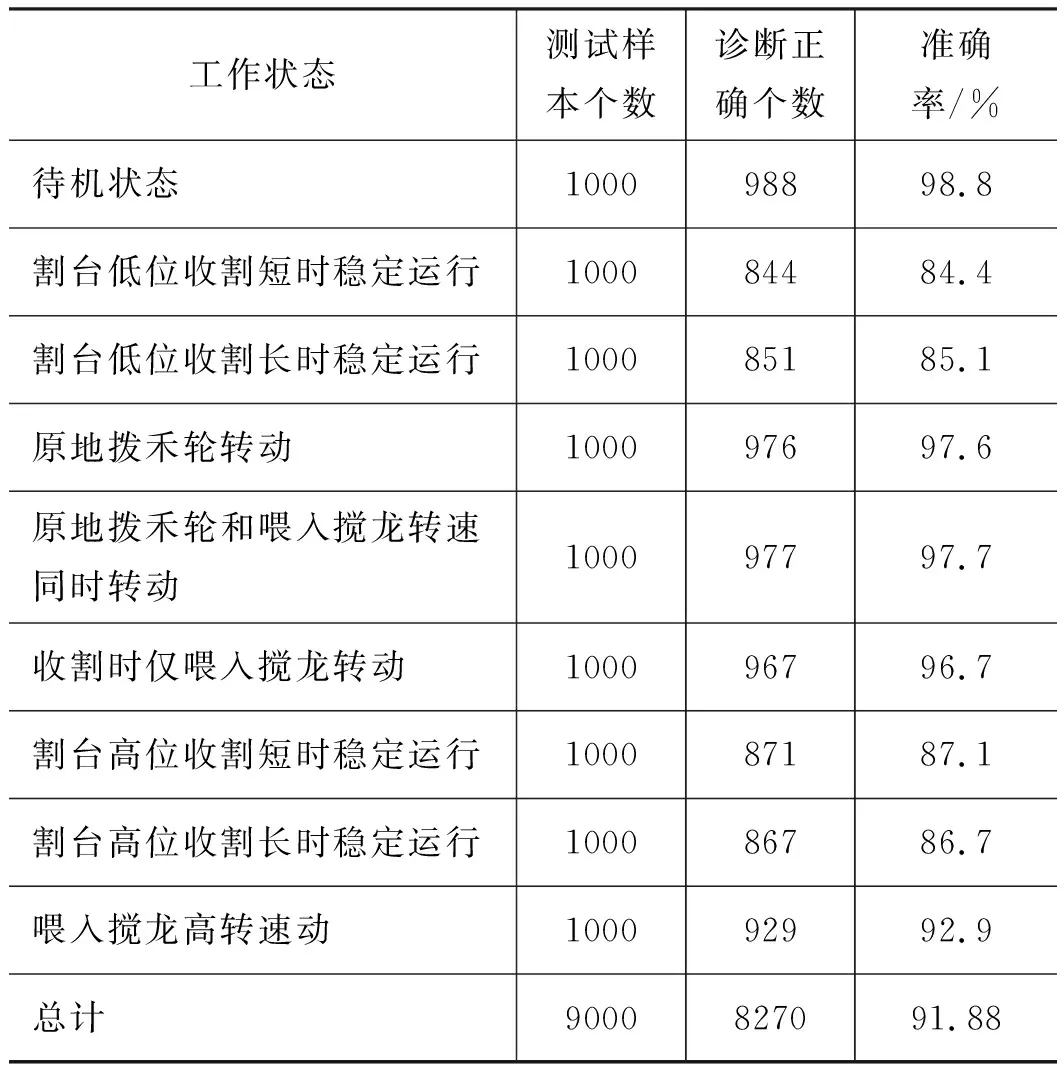
表4 SAE-DBN对联合收割机工作状态辨别结果Tab.4 Result of combine harvester's working state identification based on SAE-DBN

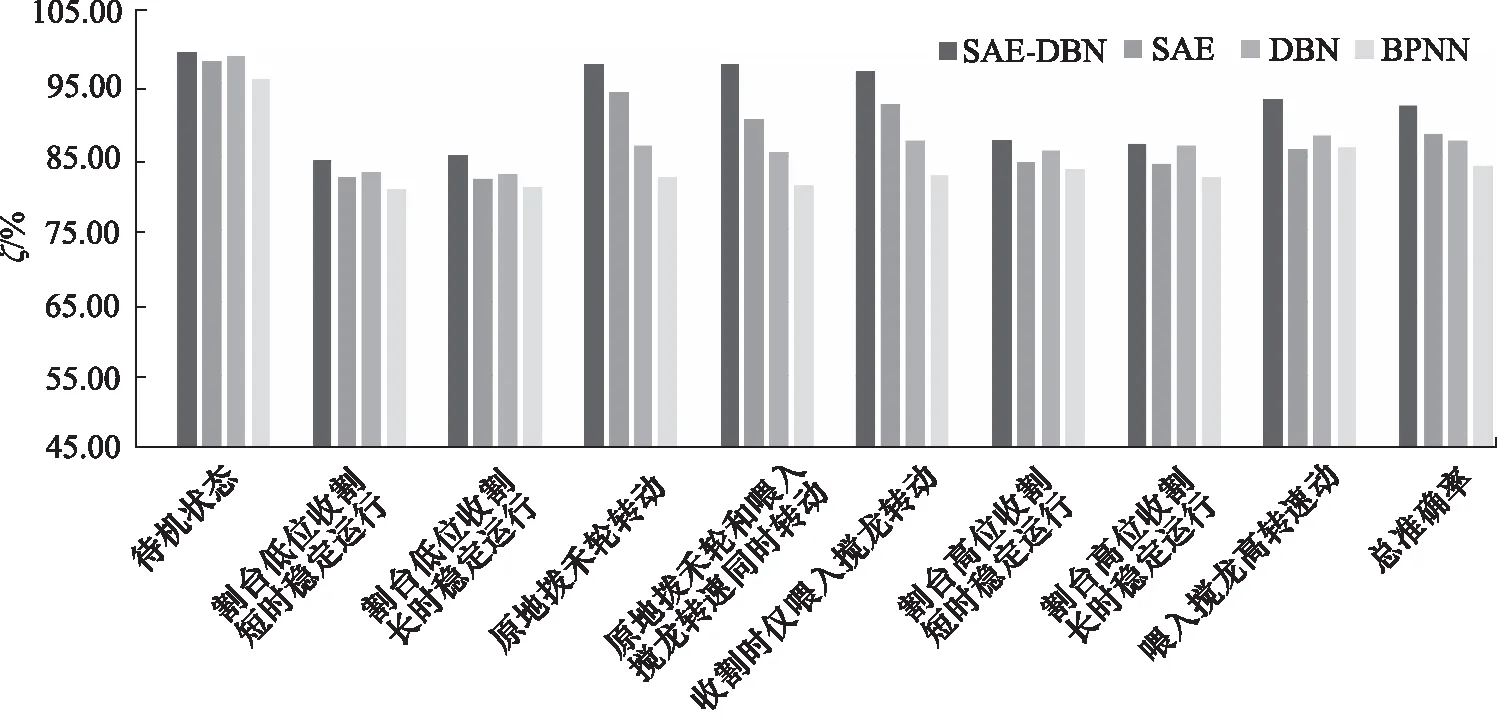
图12 SAE-DBN和SAE、DBN以及BPNN之间的比较图Fig.12 Comparison diagram between SAE-DBN and SAE, DBN and BPNN

由图12可知SAE-DBN模型准确率为91.88%，与SAE、DBN以及BPNN等相比，分别提高了3.82%，4.81%和8.09%；但是在割台低位收割短时稳定运行、割台低位收割长时稳定运行、割台高位收割短时稳定运行以及割台高位收割长时稳定运行状态下性能与其他模型相比，准确率提升不显著；在联合收割机原地拨禾轮转动、原地拨禾轮和喂入搅龙转速同时转动、收割时仅喂入搅龙转动状态下，SAE-DBN模型准确率有显著提高。

由实验结果可知SAE-DBN模型在联合收割机液压系统状态分类有优异的表现，为联合收割机液压系统故障诊断与预警提供了一种比较先进的技术手段。