膨胀土水射流清洗机理的实验及建模研究

龙品瀛， 林义忠

(广西大学 机械工程学院， 广西 南宁 530000)

引言

土方机械在作业时其触土部分不可避免的产生土壤粘附现象，土壤粘附会消耗额外的能量，降低作业效率[1-2]。如果粘附土壤质量占其工作满负荷的20%～30%，则会导致总功率的30%～50%用于克服额外的阻力[3-4]。目前土方机械的清洗主要是通过人工水射流清洗，需要消耗大量的人力物力，为了实现清洗过程的自动化和智能化，需要进一步研究水射流的清洗机理与清洗模型。

相关研究资料显示，水射流冲击靶面后，射流液体会以冲击点为中心呈辐射状散开，并且在距冲击点一定距离处出现液膜高度突然增加的水跃现象。WILSON 等[5]提出一个简单的径向流域(RFZ)模型，认为在径向流域的边缘处射流的径向动量与液膜上的表面张力相平衡，并以此预测水跃的半径。BHAGAT[6]证明了WILSON模型的准确性，并且还证明重力对径向流域内的流动影响很小。随后，WILSON[7-8]发现射流的清洁速率与单位宽度的动量流率成比例，提出射流垂直撞击靶面的清洗模型并推广到射流移动。为了解决RFZ边界内极限清洗半径问题，GLOVER 等[9]和FERNANDES 等[10]在清洗速率公式中引入经验项，该模型在工业领域得到了广泛的应用。

上述水射流清洗模型的清洗对象多为人工合成的化合物(PVA或者凡士林)，对于触土机械的水射流土壤清洗，其适用性还有待于进一步的分析和实验验证。为了更好地描述膨胀土射流清洗的机理过程，本研究在上述模型的基础上，引入了清洗阻尼系数，并修正了清洗速率公式。以华南地区广泛分布的红壤膨胀土为研究对象，采用机器视觉技术记录和分析了水射流的清洗过程，开展了在不同射流压力、射流倾角和膨胀土含水量条件下的水射流清洗实验，并将理论模型计算结果与实验结果进行对比分析，研究结果可以为触土机械的射流清洗装置设计提供一定的参考依据。

1 水射流清洗模型

国内在水射流清洗的研究多为基于计算流体力学的数值仿真分析和实验研究[11-12]，对清洗模型建模分析较少 。不同材料的水射流清洗理想模型是一致的，清洗的三种基本模型为射流静止清洗模型、射流移动清洗模型和射流倾斜清洗模型，实际工业应用的工况可表示为三种基本模型的耦合。

1.1 射流静止清洗模型

如图1，喷嘴静止清洗时，射流撞击靶面后会形成一个半径为a的圆形清洁区域[13-14]。WILSON发现土壤的清洁速率与清洁前沿处的动量流率成比例，GLOVER 等考虑土壤对清洗的阻碍作用后提出：

(1)

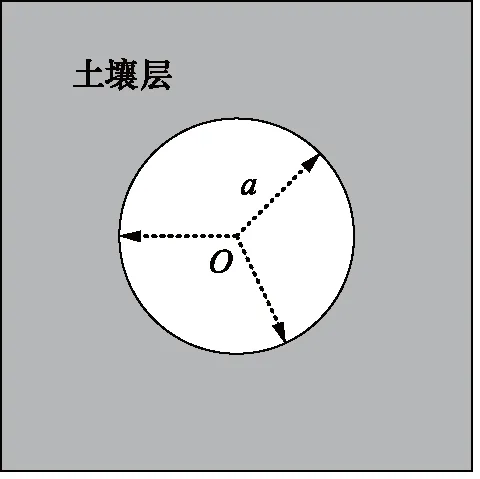
图1 喷嘴静止清洗模型Fig.1 Cleaning model of static jet

在RFZ中，a是t时刻从撞击点到清洁前沿的径向距离，k是清洁速率常数，M和M0分别是在a处每单位宽度的液体动量流和产生清洗效果而必须克服的应力，在本研究中，将引入2个更为直观的参数来表示M0。BHAGAT 等[15]将清洗模型分为强、中、弱三种土壤模型，在膨胀土的清洗实验中，与弱土壤模型吻合良好，因此以下推导均使用弱土壤模型：

(2)

解式(2)微分方程可得：

(3)

(4)

1.2 射流移动清洗模型

射流移动时，会形成一个近似椭圆形的清洁前沿和一条宽度为wc的带状清洁区域，如图2。WILSON等[8]通过速度矢量分析建模，当射流相对靶面的横向移动速度远小于射流撞击在靶面上形成的液膜的流动速度时，清洗行为由一阶非线性微分方程描述为：

(5)

(6)

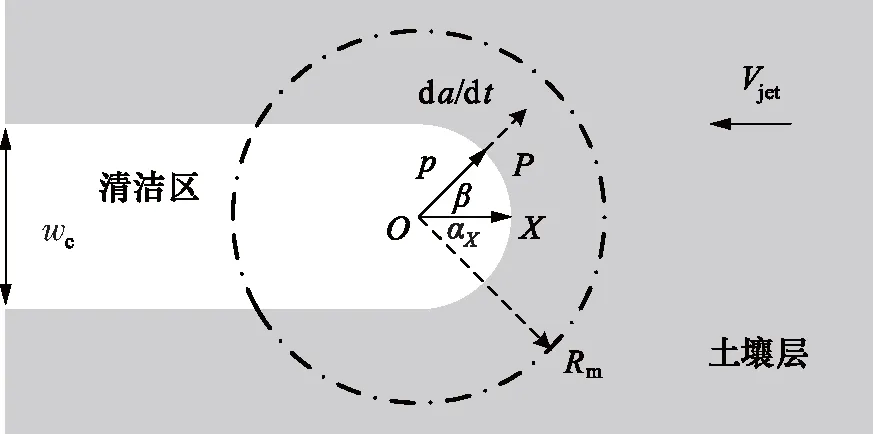
图2 射流移动清洗模型Fig.2 Cleaning model of moving jet

在清洗的正前方的点X处，此处的清洗速度等于射流的移动速度。式(6)最后一项为引入M0产生的屈服应力项。式(6)两边同乘以p3，并令p*=p4可以化为一阶线性微分方程：

(7)

由式(7)可得：

(8)

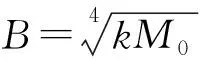
1.3 射流倾斜清洗模型

WANG等[16]对WILSON 等提出的径向流域模型进行了拓展，使得其能够适用倾斜的情况，但是其模型需要数值积分，本研究提出另一种更为方便的表示法。半径为r0的圆柱射流以角度φ(射流与靶面的夹角)撞击壁面后，产生的截面是一个椭圆。如图3所示，点S为射流撞击后产生滞止压力的位置，O为射流中心，S与O的距离为偏心距b，椭圆边缘任意一点到S的距离为q，椭圆上一点与S的连线与椭圆长轴的夹角为方位角θ，于是该椭圆截面可用以下方程描述：

(9)

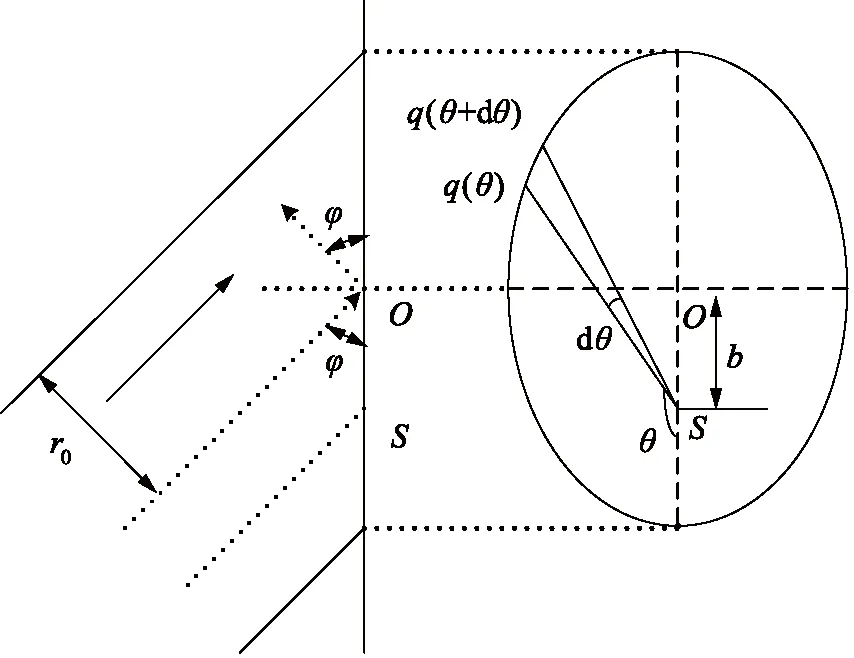
图3 倾斜射流撞击靶面的理论分析模型Fig.3 Theoretical model of inclined jet impinging on surface

椭圆边缘任意一点到S的距离为：

(10)

对于均匀流，文献[17]推导得到b=r0cosφ，式(10)简化为：

(11)

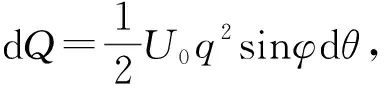
(12)

(13)

从F′的表达式可以看出，F′仅由φ和θ决定，F′可以表征倾斜角为φ时靶面上液膜流量沿不同方位角θ的分布规律。倾斜射流撞击靶面后会产生反射现象，因此实际参与清洗的为F′在靶面上的分量F=F′cosφ。于是方位角θ处的动量流量Mθ和距离滞止点rθ处的液膜平均流速Uθ为：

(14)

(15)

因此方位角θ处的清洁速率：

(16)

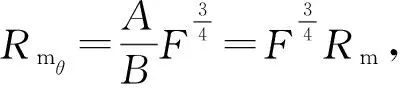
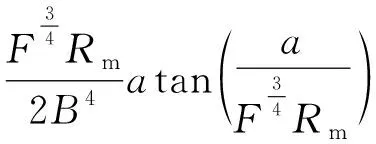
(17)

2 实验装置及实验材料

实验装置示意图如图4所示，实验时靶面的移动速度在300～1800 mm/min之间，射流压力控制在0.5～1.0 MPa。基板使用Q235钢，摄像机以60帧/s跟踪清洗过程，实验用水为城市自来水，喷嘴的孔径dN=2r0=1.2 mm，靶距(喷嘴到射流撞击点的直线距离)为20 mm，保证射流连贯而不会因表面张力而产生破裂[19-20]。启动水泵后将挡板放置在喷嘴与靶面之间至少30 s，确保形成稳定的射流后移开。

图4 射流清洗实验装置示意图Fig.4 Experimental device diagram of jet cleaning

实验材料为华南常见的膨胀土，膨胀土的物理性质指标如表1所示。膨胀土从建筑工地取得，烘干之后研磨成粉。实验时通过电子秤精确称取土和水的质量，然后混合并充分搅拌至土样无结块、大颗粒为止。膨胀土试样的含水率m控制在25%～30%之间。含水率的计算公式如下：

(18)

其中，mw是水的质量，ms是土的质量。不同的土壤层厚度对应的阻尼系数也不同，但都表现出相似的清洗行为，为了验证模型的正确性，本研究中将控制土壤层的厚度为常数。制作清洗的靶面时，将厚度为2 mm 的模具固定在基板上，然后将土样均匀地涂抹在模具内，再用一个切削板沿着模具表面切削，撤去模具后得到与模具厚度相同的土样。

表1 实验用土的物理性质Tab.1 Physical properties of nanning expansive soil

3 结果与分析

3.1 射流静止

图5是在膨胀土含水量28%、压力0.5 MPa下的清洗过程。t=0 s时清洗开始，在初始的一段时间，清洁区域的面积增长速度非常快；清洁前沿呈锯齿形，大致轮廓是比较近似的圆形，并且在清洁前沿处形成一个“堤坝”，FERNANDES 等[10]指出堤坝的形状与液膜厚度和土壤层厚度的比值有关。

图5 射流静止清洗过程Fig.5 Photograph of cleaning process of static jet

如图6所示提取出每个时刻的清洁前沿的半径，图7是各时刻清洗前沿的半径的拟合结果，通过数据拟合可以得到B=0.60，Rm=28.81，可见式(4)拟合的结果与实验数据非常吻合。图7显示两种压力条件下的Rm非常接近，其原因是当压力较大时，射流撞击靶面产生大量飞溅，造成了能量损失。尽管如此，1.0 MPa 压力下的初始清洁速度仍然比0.5 MPa要快。考虑能源的利用率，仍不建议使用较高的压力。

图6 清洁前沿的圆拟合Fig.6 Circle fitting of cleaning front

图7 0.5 MPa和1.0 MPa压力下清洁前沿随时间变化规律Fig.7 Changes of cleaning front with time at 0.5 MPa and 1.0 MPa pressures

3.2 射流移动

射流移动的实验数据均是在水平射流撞击垂直壁的条件下获得。射流的压力固定为0.5 MPa，通过靶面的水平移动产生相对运动。清洁前沿的形状通过图像处理算法提取，图8b中接近清洁前沿的曲线是式(8)预测的结果。y是清洁前沿一点在射流移动法方向到撞击点的距离，将y=psinβ代入式(5)可得：

(19)

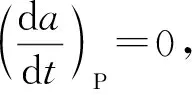
图8 射流移动清洗照片和清洁前沿的预测Fig.8 Photos of jet moving cleaning and prediction of cleaning front

3.3 射流倾斜

实验中射流倾斜角为20°～45°，射流压力为0.5～1.0 MPa。实验结果显示不同倾角和压力均有相似的清洗行为，图9是倾斜角30°，射流压力0.5 MPa的清洗过程。与射流垂直清洗类似，初始阶段清洗速度非常快，土壤在射流的冲击下快速剥落。不同的是射流倾斜清洗时不同方位角的清洁前沿半径不一致，呈近似的椭圆形。

图9 射流倾斜清洗过程Fig.9 Photographs of cleaning process of tilt jet

图10a是t=25 s时式(17)的预测结果，与实际的清洁前沿非常接近。然而式(17)的准确性并不总是有效，如图10b，t=82 s时大方位角处的清洁前沿远比预测的值要小，事实上，所有的视频均显示在接近π的方位角处都不能达到式(17)预测的位置。大方位角处，液膜流动逐渐由层流向紊流过渡，式(17)将不再那么精确。即便如此，实际应用时不大可能长时间清洗同一个位置，因此式(17)仍然适合工程应用。

图10 25 s和82 s时清洁前沿预测与实验对比图Fig.10 Comparison of prediction and experiment of clean front at 25 s and 82 s

4 结论

基于机器视觉技术研究了膨胀土在1.2 mm的喷嘴和0.5～1.0 MPa的压力下的清洗行为，实验数据与理论计算结果的一致性表明PVA或凡士林等粘塑性化合物质的清洗模型可以移植到膨胀土的水射流清洗过程，引入清洗阻尼系数可以更为直观地计算最大清洗半径，使得模型更加符合实际的生产应用情况。

清洗模型计算表明：

(1) 射流的清洗速率和清洁前沿的最大半径随着射流流量的增大而增大；

(2) 射流移动清洗产生的清洗带宽度随射流移动速度的增大而减小；

(3) 射流倾斜清洗时射流与靶面的夹角会改变液膜在靶面上的流量分布，倾斜清洗模型等效于射流垂直清洗模型乘以射流与靶面夹角有关的比例因子。