滑阀V形阀口漩涡空化数值仿真分析

陆 亮， 王 健， 凌扬洋， 李鸿向

(1.同济大学 机械与能源工程学院， 上海 200092； 2.江苏金陵智造研究院有限公司， 江苏 南京 210022)

引言

在工程机械电液控制应用中，通常使用具有节流阀口的液压滑阀进行位移-开度-流量调节，通过各种阀口的组合实现稳定的比例流量控制[1]。阀口体积较小且结构复杂，油液经过阀口时会形成射流、涡流等复杂湍流流场，并伴随空化现象等[2]。阀口是滑阀的核心结构，其流场特征直接决定节流槽式滑阀的流量控制性能。其中V形阀口节流刚度高、线性度好，多用于流量控制精度要求高的场合[3]，出现空化会破坏其控制精度。因此，对滑阀V形阀口空化形成机理及其行为机制的研究具有重要意义。

针对液压阀空化流场的研究，多采用实验观测和数值模拟的方法。杜学文等[4]采用实验方法对不同阀口结构内压力分布、气穴形态和噪声频谱进行了研究。陆亮等[5]采用实验和数值方法研究了U形阀口中空化噪声、空化形态和空化流量特性等多种空化问题。随着数值计算方法和计算机算力的不断发展，计算流体动力学(CFD)方法在研究液压元件内复杂流场细节方面提供了巨大帮助，已被应用于流场结构和液动力等多个方面的研究[6～7]。HAN等[8]选用三种不同结构的锥阀对水力液压系统中锥阀空化状态下液动力性质进行了数值方法研究，分析了几何参数和出口压力对锥阀流动特性、空化和液动力的影响。LU等[9]采用实验和数值方法分析了U形滑阀在不同背压和阀口尺寸下空化喘振特性及形成机理，并提出了抑制方法。郑智剑等[10]采用数值方法研究了液压滑阀在高压状态下的空化流动特性，分析了不同入口压力下液压滑阀内空化流场特征。张鑫等[11]采用数值方法分析了不同阀口滑阀在不同开度下压力场和空化分布及气体体积分数的变化趋势。毛伟等[12]对V形球阀进行了数值方法研究，分析了不同锥角和开度下V形球阀流场特性和空化特性的变化规律。

如上所述，现有阀口空化数值仿真研究多采用时均湍流模型，获悉空化分布与剧烈程度，其本质上是遵循哈维空化核子模式，从气核分布角度采用统计学方法认知空化。但已有不少研究采用DNS或LES模型，着重描述了流场中的漩涡特性，提出了漩涡汇聚成形空化的观点[13～14]。由此，本研究使用LES模型对V形阀口空化进行仿真建模，以此深入研究空化成形过程及其宏观尺度分布的机理与规律，为空化耦合的阀口通流设计提供理论依据。

1 滑阀流域及V形阀口结构

如图1为基于实际比例阀的单进单出液压滑阀结构，阀芯上对称分布有2个V形阀口。为节省计算资源，将图1中虚线部分作为仿真流域，并进一步定义两个对称面来简化仿真流域，如图2所示。图3为V形阀口结构，本研究中阀口长度l为5 mm，深度h为1.5 mm，开度x为3 mm，夹角θ为90°，槽弧半径R为12.5 mm。

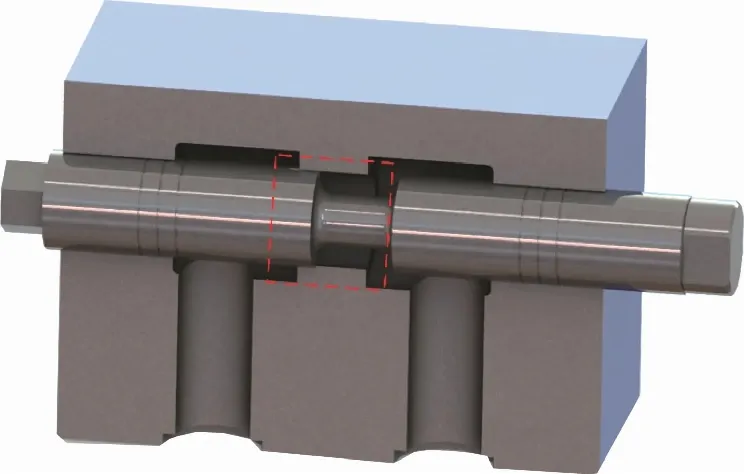
图1 液压滑阀结构Fig.1 Hydraulic spool valve structure

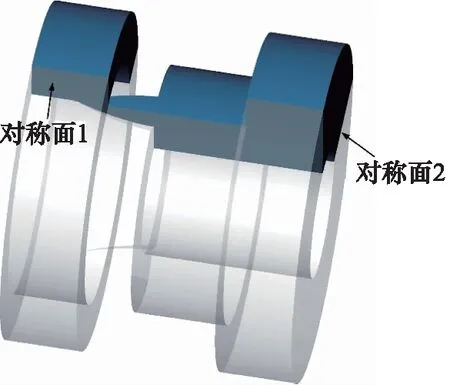
图2 简化滑阀仿真流域Fig.2 Simplified spool valve simulation flow domain

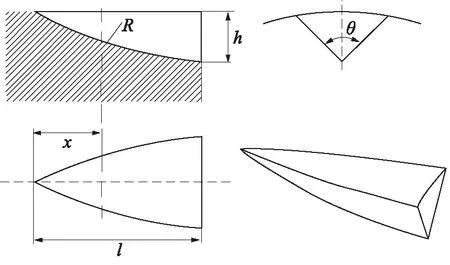
图3 V形阀口结构Fig.3 V-shape notch structure

2 数值计算方法

2.1 计算模型

液压滑阀阀口内流体为湍流运动，同时带有漩涡运动和空化现象。采用LES模型相比RANS模型能够获得更精细的流场特征和精确的漩涡结构。因此采用LES湍流模型、Mixture多相流模型和Schnerr-Sauer空化模型配合结构化网格展开研究。

2.2 控制方程

在Mixture模型中质量和动量守恒方程为：

(1)

(2)

式中，p为压力；u为速度；下标(i,j,k)表示笛卡尔坐标系的方向。混合相密度ρm和动力黏度μm为：

ρm=ρlαl+ρvαv

(3)

μm=μlαl+μvαv

(4)

式中，ρl，ρv—— 分别是液体和气体密度

μl，μv—— 分别是液体和气体动力黏度

αl，αv—— 分别是液体和气体体积分数

对式(1)和式(2)经滤波处理后可得LES控制方程为：

(5)

(6)

式中，τij为亚格子尺度应力，体现了小尺度涡对大尺度涡运动的影响，根据亚格子尺度(SGS)模型可表示为：

(7)

Schnerr-Sauer空化模型的质量输运方程为：

(8)

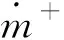
(9)

(10)

式中，空泡半径Rb与气体体积分数αv和气核数密度nb有关，可表示为：

(11)

2.3 边界条件

入口边界设为3.0 MPa压力入口，出口边界设为0.1～1.0 MPa压力出口，流域壁面设为无滑移固定壁面，求解算法采用压力基的耦合(Coupled)算法，流体介质参数如表1所示。

表1 流体介质参数Tab.1 Fluid parameters

2.4 网格划分

节流槽结构复杂，往往使用非结构化网格进行划分，但LES湍流模型需要高质量的网格进行计算，因此采用结构化网格进行划分。结构性网格中分块的好坏直接决定了网格质量，因此分块尤为重要。如图4a为整体分块方案，总共有30个六面体块，其中V形阀口结构最复杂，采用了7个块进行划分如图4b所示。该分块方案可使越接近V形阀口网格越密，能够更好的捕捉阀口附近流场特征。

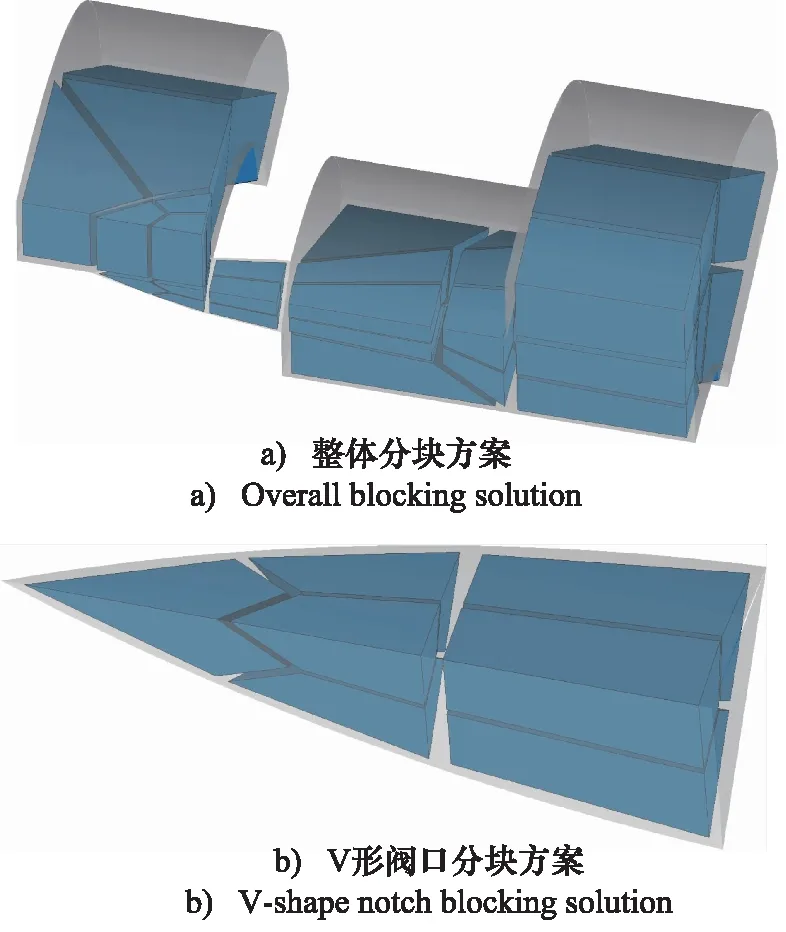
图4 1/4滑阀流域分块方案Fig.4 1/4 spool valve flow domain blocking solution (x=2 mm)

为验证网格独立性，在相同的边界条件和仿真参数下，使用商业软件ICEM设置了6种网格密度进行对比仿真如表2所示，并进一步展示了6种网格的网格质量，均符合计算要求。图5展示了不同网格密度下的时均流量，网格数为n。可以发现，从网格1到网格5时均流量变化较大，但网格5之后流量基本不变。因此可认为当网格密度大于网格5时就满足网格独立性。

表2 六种网格密度及质量Tab.2 Six grid densities and quality

图5 不同网格密度时均流量对比Fig.5 Comparison of time-averaged flow rate at different grid densities

图6展示了网格密度为网格5时流域结构化网格划分结果，可以看出V形阀口处网格密度最高。一般LES要求y+值为1左右，不能超过5。所用网格划分方式生成的网格中98%的网格y+值小于2，同时最大不超过5，满足LES的仿真要求。图7中对比了不同出口压力下实验和仿真时均流量大小，可以看出在不同出口压力下实验和仿真时均流量变化规律一致，且最大偏差σ小于5%，这验证了仿真模型的合理可靠性。

图6 结构化网格结果及细节Fig.6 Structured mesh results and details

图7 实验和仿真时均流量对比Fig.7 Experimental and simulation time-averaged flowrate comparison

3 结果分析与讨论

3.1 滑阀阀腔漩涡运动

图8展示了滑阀阀腔中的涡核心区(以Q判据水平值0.045等值面表示)变化的瞬态过程，并在涡核心区表面展示了压力云图。可以看出涡主要分布在阀口上半部分和阀腔中，其中阀口上半部分的涡是连续分布的，而阀腔中的涡则是离散分布的。如图9a所示，当流体从入口边界进入阀口时会发生流束收缩并脱离上边界，使得阀口下半部分流体速度迅速增加，而上半部分流体速度则基本不变，阀口上下部分流体之间形成巨大的速度梯度，在剪切应力的作用下阀口上半部分流体形成稳定的漩涡运动。高速流体从阀口进入阀腔为自由射流运动，会与阀腔周围静止流体形成速度不连续的间断面，在剪切应力作用下速度间断面会变得不稳定，进而引起流体波动并发展成漩涡，阀腔中的离散漩涡即为射流漩涡配对生成。

如图8所示，在T0时刻阀腔中存在5个涡，其中涡1在阀腔中刚开始形成，涡2处于发育阶段，涡3～5均已基本发育完成，在T0～T0+42 μs这段时间内5个涡均向后运动， 并且涡1～4位置逐渐变的和T0时刻涡2～5类似，涡5则向后运动脱离阀腔，在T0+42 μs时刻又在阀腔中形成一个新的涡0，对应T0时刻的涡1。之后在T0+ΔT(42 μs)～T0+ΔT+42 μs时间内又重复展现了这一涡运动过程，可以得出在当前流场参数中涡的运动周期约为42 μs。

图8 涡核心区周期性运动过程(pout=0.6 MPa)Fig.8 Periodic motion process of vortex core region (pout=0.6 MPa)

图9b展示了T0时刻阀腔中涡核心区(表面无压力云图)和对称面1(图6)处压力云图，可以看出阀口上半部分压力均较低，因为漩涡中心的压力较低且阀口上半部分漩涡是连续分布的；阀腔中大部分区域压力和出口压力接近，而涡分布区域则压力较低，两涡中间区域则压力较高。阀腔中涡在向后运动过程中必然会引起阀腔各处压力变化，为此在阀腔中取四个点(图9b中y值为距V形阀口出口距离)以分析其压力时域信息如图10a所示。可以发现各点存在周期性的压力脉动，在对各点时域压力统一减去出口边界压力(0.6 MPa)后再进行快速傅里叶变换进一步获得其压力频域信息如图10b所示。可以发现点1处由于无漩涡运动而没有压力脉动，其余3点压力脉动主频一致，约为23.35 kHz。根据图8得出的涡运动周期约为42 μs，换算为频率则约为23.81 kHz。二者频率十分接近，可以说明正是阀腔中漩涡的运动过程引起了阀腔中压力脉动。

图9 阀腔对称面1处流场特性(pout=0.6 MPa)Fig.9 Flow field characteristics at the symmetry 1 of valve chamber(pout=0.6 MPa)

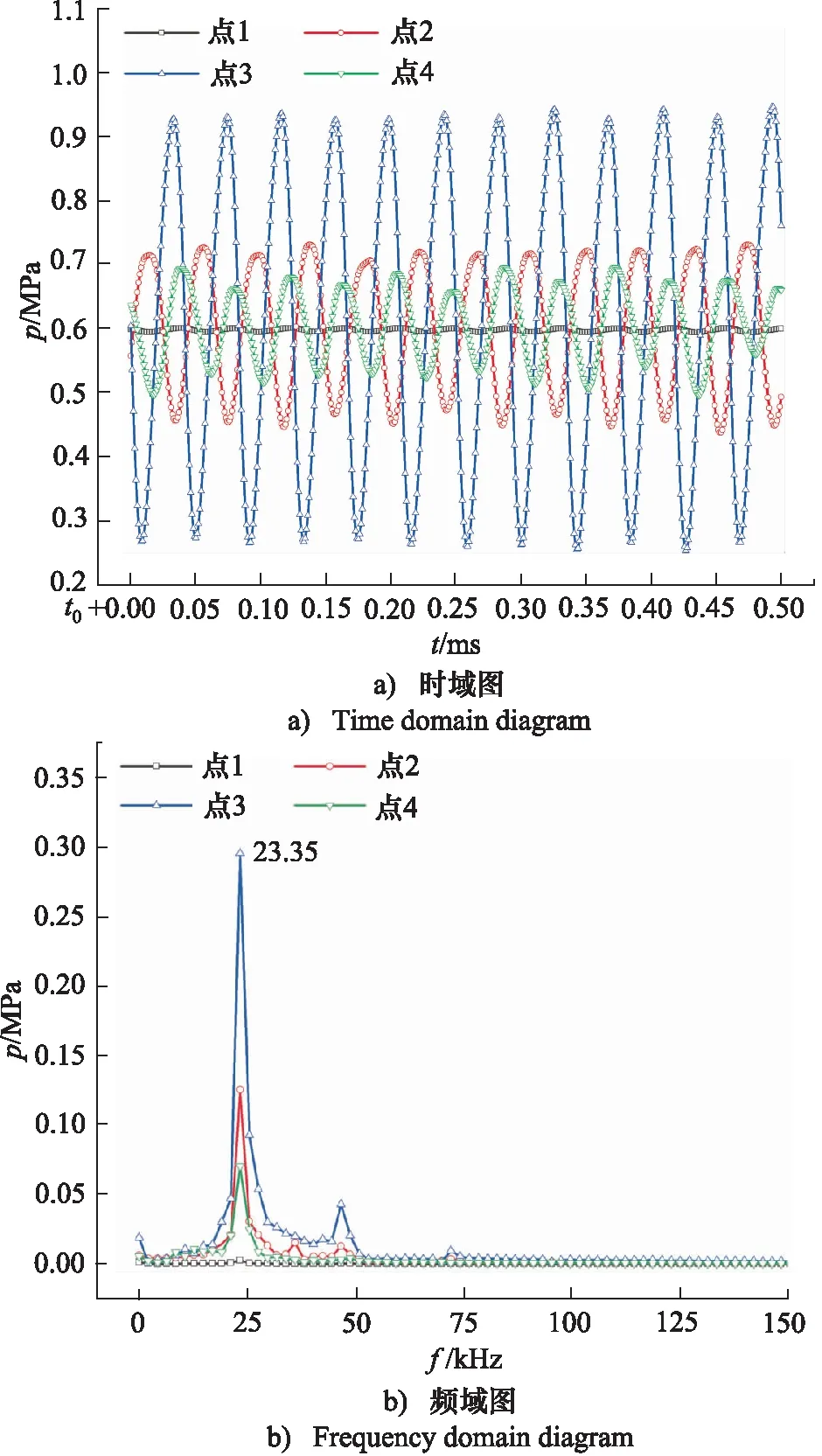
图10 阀腔压力脉动特性(pout=0.6 MPa)Fig.10 Valve chamber pressure fluctuation characteristic (pout=0.6 MPa)

3.2 出口压力对滑阀流场特性的影响

图11展示了不同出口压力下阀腔中图9b虚线上四个点位置的压力时域图，可以发现在出口压力较高时(图10a、图11d)阀腔中各点存在周期性的压力脉动，压力脉动为漩涡运动单独引起。随着出口压力降低(图11a～图11c)压力脉动逐渐变得无周期性。这是由于随着出口压力降低，一方面进出口压差增大使阀口射流速度增加，漩涡强度增强从而使得压力脉动幅度增大，另一方面压力脉动的基准值(出口压力)也在降低。这两方面使得阀腔中更易出现低压区域，为空化的产生创造了合适的条件，空化出现后也会引起阀腔中压力变化，在空化与漩涡运动耦合作用下破坏了阀腔中原本漩涡运动单独引起的压力脉动周期性。

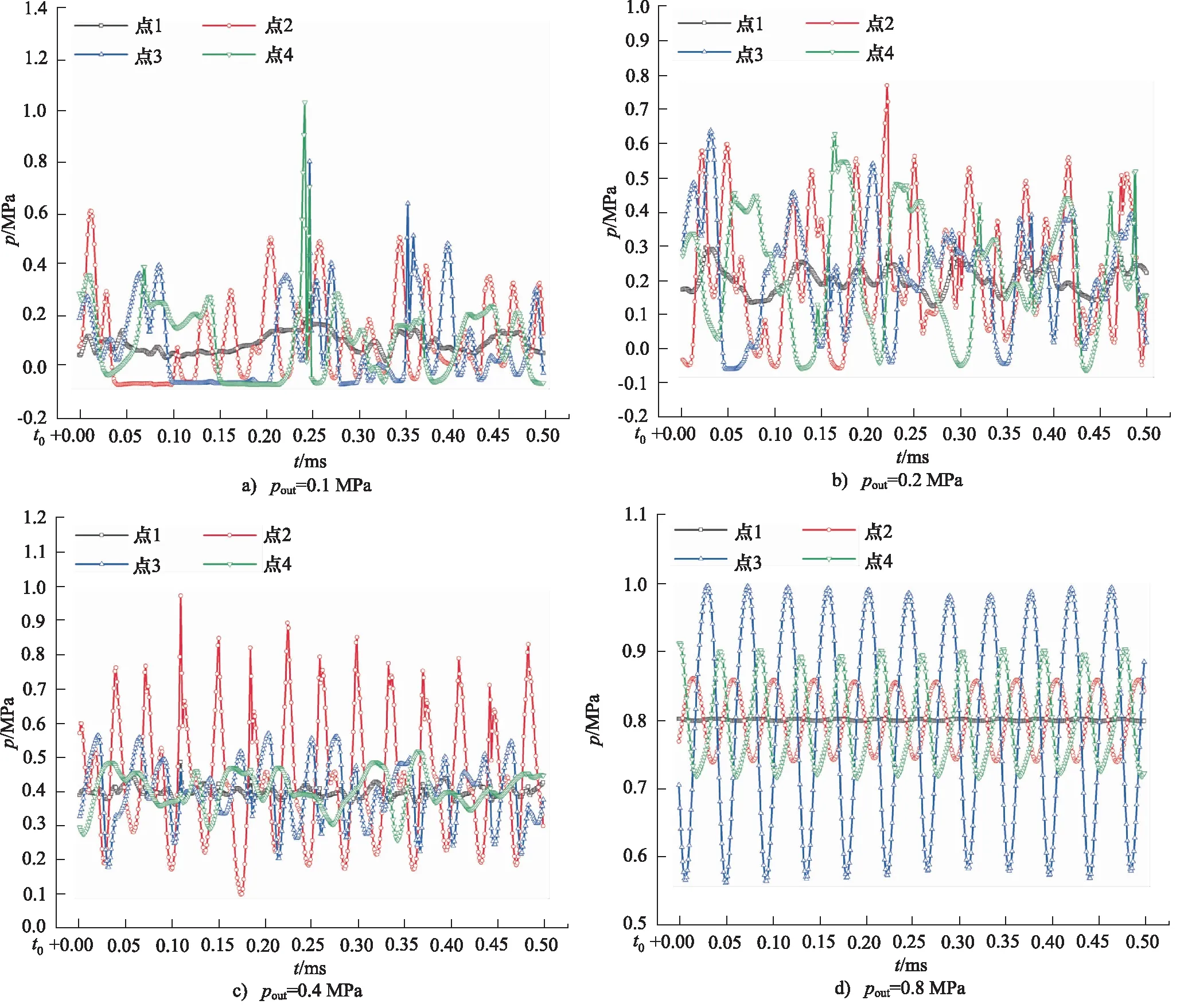
图11 不同出口压力下阀腔中各点压力脉动时域图Fig.11 Valve chamber pressure fluctuation time domain diagram at various points with different outlet pressure

图12a展示了滑阀流域内数个切片上的气体体积分数云图，图12b展示了滑阀流域内气体体积分数0.3等值面，可以看出二者形状和位置十分接近，因此后续分析中统一采用气体体积分数为0.3的等值面图像以表示滑阀流域内的空化。如图13展示了不同出口压力下阀腔中的空化图像，可以看到在出口压力较高时(图13c和图13d)阀腔中没有空化，压力脉动只由漩涡运动引起存在明显周期性， 随着出口压力降低(图12b、图13a和图13b)阀腔空化变得明显，压力脉动也变得无明显周期性。需要指出的是在出口压力为0.4 MPa时阀腔中四点压力在时域上均高于0.1 MPa但阀腔中也有空化出现是因为空化存在区域与4点位置不同。

图12 滑阀流域空化分布(pout=0.1 MPa)Fig.12 Spool valve basin cavitation distribution (pout=0.1 MPa)

图13 不同出口压力下空穴图像Fig.13 Cavity images at different outlet pressure

根据图10a和图11c可以发现阀腔无空化时点3位置的压力脉动幅值较大，因此选取点3代表不同出口压力下的主频以分析出口压力对漩涡运动压力脉动主频的影响，如图14所示。可以发现随着出口压力降低，压力脉动的主频升高。因为出口压力较低时射流速度更快，使得漩涡运动的速度更快，因此压力脉动主频更高。

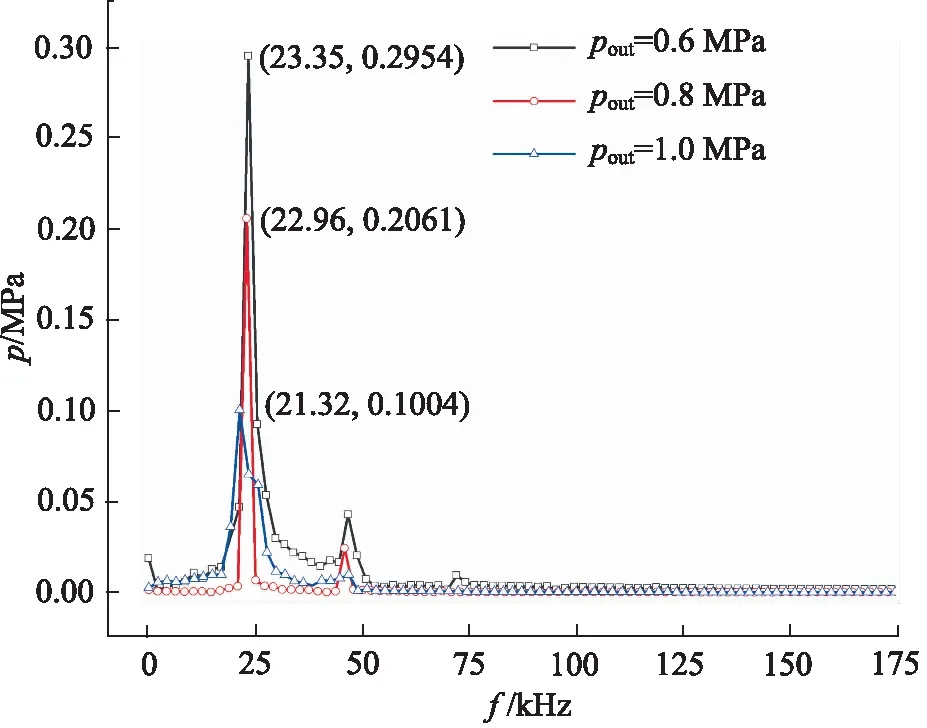
图14 出口压力对漩涡运动压力脉动主频影响(点3)Fig.14 Effect of outlet pressure on vortex motion pressure pulsation main frequency (point 3)

3.3 V形阀口空化机制

根据以上讨论，选取出口压力0.1 MPa案例来分析V形阀口滑阀的空化机制。如图12b中所展示的滑阀流域内的空化图像，可以看出空化主要存在于V形阀口节流边后上半部分和阀口后的阀腔中。图15和图16分别展示了滑阀流域内的压力和涡核心区与气体体积分数等值面分布情况。可以看出涡核心区基本覆盖了空化部分，且空化均出现在离散涡的中心处。当流体从入口边界进入阀口时会发生流束收缩并脱离上边界，在剪切应力的作用下阀口上半部分流体形成稳定的漩涡运动(图16)，漩涡中心的持续低压导致阀口中空化发生(图15)。当流体从阀口射流进入阀腔中后，会在阀腔中引起漩涡配对现象，使得阀腔中生成离散的漩涡(图16)，漩涡运动会引起阀腔中压力脉动(图15)，压力脉动低压导致阀腔中生成离散的空穴。

图15 滑阀流域压力云图(pout=0.1 MPa)Fig.15 Spool valve flow domain pressure contour (pout=0.1 MPa)

图16 涡核心区和空化区域对比(pout=0.1 MPa )Fig.16 Comparison between vortex core region and cavitation region (pout=0.1 MPa)

4 结论

在本研究中，使用大涡模拟和结构化网格对V形滑阀进行了数值方法研究，根据研究总结如下。

(1) V形阀口节流边后上半部分在剪切应力作用下形成漩涡运动，漩涡中心的低压引起阀口漩涡空化。阀腔中离散生成的漩涡在向后运动过程中会使阀腔产生持续的压力脉动，在压力脉动剧烈时会在阀腔中产生离散的空化。

(2) 阀腔漩涡运动引起的压力脉动具有固定主频，且阀腔各处主频一致，该主频随出口压力降低而增加。阀腔中出现空化后会破坏压力脉动的周期性。