遗传算法下弧齿锥齿轮齿面接触特性优化
2022-04-19姜志宏王兴卫池汉佳赵小涛
姜志宏,王兴卫,池汉佳,赵小涛
(江西理工大学 机电工程学院, 江西赣州 341000)
弧齿锥齿轮副的传动性能表现在齿面接触迹线的角度、接触区的大小及传动误差,可通过调整机床初始加工参数进行修正[1]。Argyris等[2]采用集成的计算机优化方法,对弧齿锥齿轮轮齿间的应力进行分析。Artoni等[3-4]提出一种自动程序来优化加载情况下的齿面接触区域,该程序能够识别接触区图案的形状并对其进行优化。严宏志等[5]定义出最佳齿面修形量,以最小化LTE和降低接触压力,同时将加载的接触区约束在齿面规定的区域内,可避免任何边缘或角接触。Samani等[6]提出了生成最佳弧齿锥齿轮齿面的方法。杨林和刘大鹏[7]通过对小轮控制参数的不断调整,使实际接触区域和传动误差达到较为理想的状态。王琪等[8]研究了弧齿锥齿轮齿面加载性能多目标优化问题数学模型的建立及求解。张卫青等[9]提出基于共轭差曲面的弧齿锥齿轮接触特性的控制方法。刘卫平等[10]基于机器视觉技术快速获得弧齿锥齿轮的齿面接触区,并通过计算齿面接触区偏离齿面型心的程度及齿面接触区的二维分形维数达到评价齿轮质量的目的。周凯红等[11]通过点啮合齿面加载接触的实验数据,建立了点啮合齿面整体优化设计的变分不等式模型。
本文通过一种基于遗传算法的弧齿锥齿轮齿面接触区和传动误差曲线的全局优化设计方法,以提高摆辗机弧齿锥齿轮性能。
1 控制参数及优化目标的确定
传统的TCA技术仅是在轻载的情况下对齿面进行接触分析,不合理地修改大轮和小轮的机床调整参数会导致各种类型的传动误差曲线,包括直线形误差到“S”形误差,对称的误差到不对称的误差;计算弧齿锥齿轮刀具参数和机床调整的传统方法只能控制计算点的法向量和曲率,而不能保证整个齿面接触,使齿面接触区的位置、大小和形状出现如对角接触、菱形接触、鱼尾形等不良接触[12]。
1.1 控制参数的确定
小轮的螺旋角 βP、小轮的节锥角 Γp、小轮的节锥距Rp、齿高方向的法曲率Ap、齿长方向的法曲率Bp和短程挠率Cp都可以作为优化问题的控制参数。然而,前3个参数只与大轮轮坯有关,而与齿形无关。小轮在节点P(小轮节锥与大轮节锥的切点)处齿高方向的法曲率Ap、齿长方向的法曲率Bp和短程挠率Cp是确定小轮切齿节锥的主要因素。因此选Ap、Bp、Cp作为优化问题的控制参数,符合啮合特性主要由齿面曲率决定的原则[13]。
1.2 确定优化目标
齿面接触区和传动误差曲线存在多种缺陷形式,采用尽量少的优化目标,限制尽量多的缺陷种类,选择瞬时接触椭圆长半轴、接触迹线方向角及传动误差曲线交叉点纵坐标作为优化目标。
1.2.1 瞬时接触椭圆长半轴l
瞬时椭圆长半轴l可以控制接触区域的大小,防止接触区出现宽接触、窄接触、长接触和短接触等不良现象。瞬时接触椭圆长半轴最优值为

式中:F为齿长接触系数;b为 齿宽;β为螺旋角。
由于啮合周期内有无数的瞬时接触椭圆,且每个椭圆长半轴的长度是不一样的,因此瞬时接触椭圆长半轴l可用平均值表示,即

式中:lk为第k个瞬时椭圆长半轴最优值;n为啮合周期内瞬时椭圆的数量。
1.2.2 接触迹线方向角γ
方向角 γ为接触迹线与根锥母线夹角。当大轮齿面为凸面且 γ <0时,传动误差曲线不相交;当γ>0时,传动误差曲线的重叠部分随着 γ的增大而增多,这表明齿轮传动的接触比在不断增大,但是过大的 γ将会导致接触区出现严重的内对角接触现象,同时对齿轮副安装精度要求极高。而当大轮齿面为凹面,情况与上述正好相反。因此 γ的最优值为:

可以看出:γ可同时影响着接触区域和转动误差曲线。虽然 γ可以防止转动误差曲线出现不重叠的现象,但是不能有效地防止传动误差曲线出现不相交的现象。将接触迹线上的接触点进行线性拟,即

式中 :Pax和Pay分 别为 接触 点在x轴和y轴 的位 置;ci为第i个接触迹线函数拟合系数。
因此接触迹线方向角 γ可表示为

1.2.3 传动误差曲线交叉点纵坐标δ
δ可避免转动误差曲线形状出现向上弯曲、不重叠、不相交等现象。 δ应为负且绝对值尽可能小,使实际传动比接近理论值。但 δ绝对值过小将导致转动误差曲线出现弯曲向上的现象。因此 δ的最优值δOPT∈ [−6×10−5−4×10−5]。
采用多项式函数表示传动误差曲线,即

式中:cj为传动误差曲线拟合系数; ψg为大轮齿面上任意接触点从机床调整位置到接触位置所需旋转的角度。
可求解得到转动误差曲线交叉点纵坐标 δ为
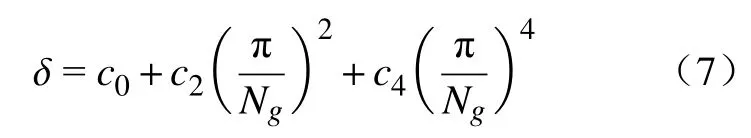
式中Ng为接触点M在大轮上的法向矢量。
2 设计优化算法
理想的齿面接触效果应使接触轨迹线为近似垂直于根锥的直线,毎个瞬时接触椭圆的长轴应大致相等,传动误差曲线应向下弯曲且能够相交,交点尽量靠近横坐标等[14-15]。
2.1 建立目标函数
有3个优化目标:lOPT、 γOPT和 δOPT。显然,要实现总体优化目标,l、γ和 δ应分别达到目标值。因此全局优化的目标函数设置如下:

式中: Δ ε为优化精度;当f(l,γ,δ)=3Δε时表明优化目标得到了总体优化。
2.2 约束条件
接触点M的位置应在大轮和小轮的齿面范围内。接触点接触点位置如图1所示。

图1 接触点位置
假设大轮和小轮的齿面在轴截面内的面积分别是 ΔSg和 ΔSP,则:

式中: ΔStop为接触点M和齿高线划分的三角区域 ;ΔStoe为接触点M和齿面小端划分的三角形区域;ΔSroot为接触点M和齿根线划分的三角形区域;ΔSheel为接触点M和齿面大端划分的三角形区域。
若接触点M超出大齿轮齿面的范围(见图1b)),则

若接触点M超出小齿轮齿面的范围(见图1b)),则
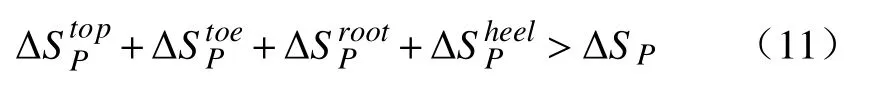
2.3 优化方程的求解
采用二进制编码的方法对控制变量进行编码;适应度函数fitvalue(l,γ,δ)= −lg(f(l,γ,δ)); 选择操作中采用“轮盘赌法”的方法,种群中每个个体被选中进入下一代的概率为Pi,计算公式为
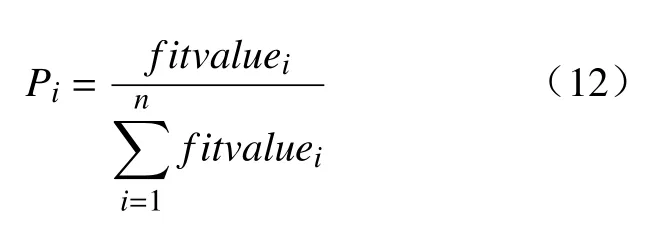
设置遗传算法参数为:种群m=30,种群内交叉概率Pc=0.6,种群内变异概Pm=0.09,选择最大代数m作 为终止准则,终止迭代数为 2 50。齿面接触区域和传动误差曲线优化方程的求解过程如图2所示,优化结果如图3所示。

图2 齿面接触区域和传动误差曲线优化方程的求解过程

图3 基于遗传算法的齿面接触区及传动误差曲线优化结果
优化目标lOPT=3.0036mm,γOPT=59.9693°,和δOPT=−5.00077×10−5rad ,计算精度Δ ε=0.001,曲率参数AP=−0.0026、BP=0.031988和CP=−0.01723,其优化后小轮机床加工参数修正量如表1所示。迭代具有良好的收敛性,这表明优化目标、控制参数和优化算法是匹配的。

表1 优化后小轮机床加工参数修正量
3 优化结果验证
3.1 有限元模型的构建
建立优化后摆辗机弧齿锥齿轮传动有限元模型,重合度 ε =1.6134,简化成两对齿啮合,见图4。选用ANSYS对整体模型进行面映射网格划分,对其中一对接触齿面进行局部网格细化,见图5。

图4 摆辗机弧齿锥齿轮简化模型图

图5 小轮接触齿面局部网格细化
3.2 大轮齿面接触区
图6是负载扭矩Tg对大轮凸面接触区的影响。
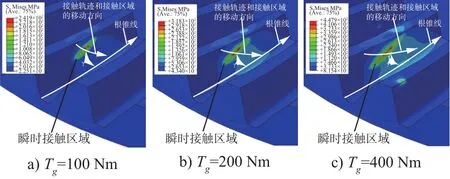
图6 负载情况下大轮凸面接触区
从图6中可以发现:
1)当Tg=100Nm时,齿面载荷由齿面中心部位最大值 2 41.9MPa向四周扩散,并有向齿根处发展趋势,其数值逐渐减小至 2.016MPa ;2)当Tg=200Nm时,齿面载荷由齿面中心部位最大值 3 18.3MPa向四周扩散,扩散到齿根处,在该部位的齿面载荷载荷为7.959Nm,但其接触区的面积和接触迹线长度有明显增加,接触迹线方向角γ 明显减小;3)当Tg=400Nm时,齿面载荷由齿面中心部位最大值 3 18.3MPa向四周扩散,扩散到齿根处,在该部位的齿面载荷增大到14.93MPa,但其接触区面积和接触迹线长度继续增加,接触迹线方向角 γ继续减小。
结果表明,齿面载荷分布均匀,变化平稳,齿面接触区基本呈椭圆形分布在大轮凸面中心区域,与优化结果(Tg=0)一致,验证该优化方法的正确性。对于齿面接触区面积、接触迹线长度及其方向角变化,说明接触区随着负载扭矩的增加,逐渐向齿根部位扩展,而不向齿面小端扩展。在实际应用中,可充分利用整个齿面的承载能力,齿轮传动装置的安装位置应到达靠近齿面小端的轻载接触区域。
3.3 传动误差曲线
负载情况下齿轮传动的传动误差曲线及瞬时传动比如图7所示。

图7 负载情况下齿轮传动的传动误差曲线及瞬时传动比
由图7a)知:传动误差曲线为理论值时,传动误差最大值为− 4.64×10−11rad,最小值为− 5.743×10−5rad,波动值为 5.743×10−5rad,呈周期性变化。
Tg=100Nm时,传动误差最大值为3.055×10−8rad,最小值为 − 2.351×10−5rad,波动幅值相比理论值增大到 2.3541×10−5rad,其曲线在一个运动周期中有3个波动区域,表示齿轮传动的啮合状态为单齿啮合与双齿啮合之间不断切换。Tg=200Nm时,传动误差最大值为− 2.973×10−8rad ,最小值为− 3.279×10−5rad,波动幅值相比理论值增大到 3.260×10−5rad,其曲线在一个运动周期内也有3个波动区域。Tg=400Nm时,传动误差最大值为 − 2.053×10−7rad,最小值为−5.431×10−5rad,波动幅值相比理论曲线增大到5.4105×10−5rad,曲线在一个运动周期内不包含明显的波动区域,运动跃迁变得更平滑,是因为啮合状态变为双齿啮合或三齿啮合,其小轮工作转角的取值、工作齿面啮合位置和轮齿间载荷分配发生了变化。
当Δi=ΔψP/Δψg在理论值2.083附近波动(图7b))。Tg=100Nm时 , Δi=0.006; 当Tg=200Nm 时 , Δi=0.006;Tg=400Nm时 , Δi=0.009。说明,当Tg增加到一定值, Δi振幅会随着Tg的增加而增加,这意味着齿轮传动的稳定性降低。
4 结论
1)提出以瞬时接触椭圆长半轴、接触线方向角和传动误差曲线交点纵坐标为优化目标,基于遗传算法的摆辗机弧齿锥齿轮齿面接触区和传动误差曲线全局优化算法,并得出优化后的齿面接触迹线方向、齿面接触区大小和传动误差曲线交叉点位置数值均在合理范围内。
2)通过建立优化后弧齿锥齿轮副系统有限元模型,并对负载下瞬态接触特性进行分析,齿面载荷分布均匀、变化平稳,齿面接触区基本呈椭圆形分布,其传动误差曲线的整体变化趋势与优化后的理论传动误差曲线基本保持一致。
