矿用提升机减速器复合故障的分段融合诊断方法

于宁，金宁，陈洪月

（辽宁工程技术大学 机械工程学院，辽宁阜新 123000）

矿用提升机减速器为重载、低速传动系统，齿轮、轴承等核心零件极易发生疲劳失效，导致减速器发生复合故障[1]。在对减速器故障问题进行诊断、识别的过程中，由于故障的结构、位置不同使得故障成分的特征信号差异较大，复合故障中弱故障成分信号往往会被强故障成分信号及噪声信号所淹没，使得故障特征难以提取，故障诊断困难[2]。因此，对矿用提升机减速器的复合故障进行精确诊断与辨识对提升机减速器的健康状态评估及煤矿安全生产意义重大。

Endo 和 Randall[3]首次将最小熵解卷积方法（MED）应用于齿轮传动的故障诊断。汪洋和郭利进[4]针对新型DSCNN-GRU结构，提出了一种基于Tensorflow与Keras深度学习平台的故障诊断模型。Purushotham等[5]采用小波分析和隐马尔可夫模型对滚动轴承元件综合故障诊断问题进行了研究。McDonald等[6]提出采用最大相关峭度解卷积方 法 （Maximum correlated kurtosis deconvolution,MCKD）研究齿轮故障问题。Shao等[7]通过采用PSO算法对深度置信网络进行改进，从而实现轴承故障诊断。Meng等[8]结合小波分析和集合经验模式分解，研究了轴承综合故障诊断问题。王宏超等[9]针对轴承故障诊断问题，提出了一种强抗噪时频分析方法。朱丹宸等[10]以滚动轴承为研究对象，基于故障信号特征提出一种基于自适应最大二阶循环平稳盲卷积和互相关谱的故障诊断方法。刘旭南等[11]基于虚拟样机技术，通过对故障信号进行小波包分解，采用神经网络算法构建了采煤机截割部齿轮传动系统故障诊断模型。赵小强等[12]基于粒子群优化细菌觅食算法（PSO-BFA）和第二代卷积神经网络（Alexnet）算法对复杂工况下滚动轴承进行故障状态辨识。陈鹏飞等[13]基于LMD-SVM方法，对航空发动机减速器一级齿轮的轮毂裂纹故障进行了诊断、识别。

以上研究对于齿轮与滚动轴承的复合故障研究尚存在不足。而矿用提升机减速器由于工况环境恶劣，存在的故障类型往往是复杂的、多样的，为对矿用提升机减速器复合故障进行精确诊断与特征辨识，基于CMF模态分解提出一种分段融合的故障诊断方法。利用CELMD和MPE计算对低频啮合分量进行包络分析；利用MCKD和Average Infogram对高频共振分量进行包络分析，最后对分析结果融合、辨识，通过搭建减速器故障模拟实验台进行验证，为矿用提升机减速器的复合故障的快速、准确诊断提供了参考。

1 矿用提升机减速器复合故障诊断的分段融合方法

在矿用提升机减速器复合故障振动信号特征中，低频分量主要集中在各阶啮合调制频带，高频分量主要集中在系统共振调制频带。因此，首先将原始振动信号分解为高频共振带和低频啮合带，再分别进行处理和包络分析。

1.1 原始信号故障特征分解

组合模态函数(CMF)方法可在一定程度上抑制经验模态分解(EMD)产生的模态混叠现象，避免振动信号中因大量间断性噪声信号干扰而产生的误诊现象[14]，其基本原理为：将含有低频和高频的若干IMFs分量组合成两个IMF。利用CMF分解得到低、高频分量分别为：

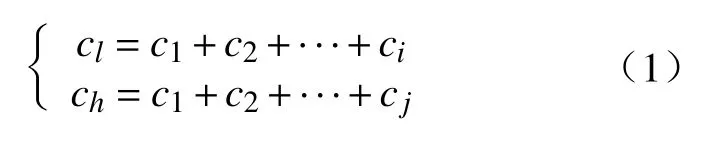
式中：cl为低频分量；ch为高频分量；i，j分别为低频和高频的IMFs分量点数。

1.2 低频信号故障特征提取

为获得可供多尺度排列熵法(MPE)计算的PF分量，且保证信号的完整性，对低频分量cl采用改进局部均值分解(CELMD)法进行再分解。CELMD分解步骤[15-16]为：

1）对低频分量cl(t)中添加白噪声序列+n1(t)，即

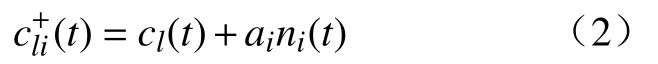
2）对添加白噪声的序列进行局部均值分解，得出第一组PF1i和余项u1；

3）对目标函数x(t)中添加白噪声序列–n1(t)，即

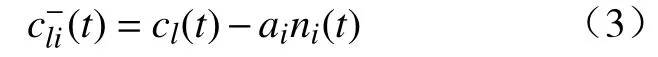
4）与步骤2）相同，对添加白噪声的序列进行局部均值分解，得出第二组PF−1i和余项u−1；

5）重复执行步骤 1）~步骤 4）；

6）将得到的两组PF分量和余项u进行求和即可得到分解后的信号分量，即：

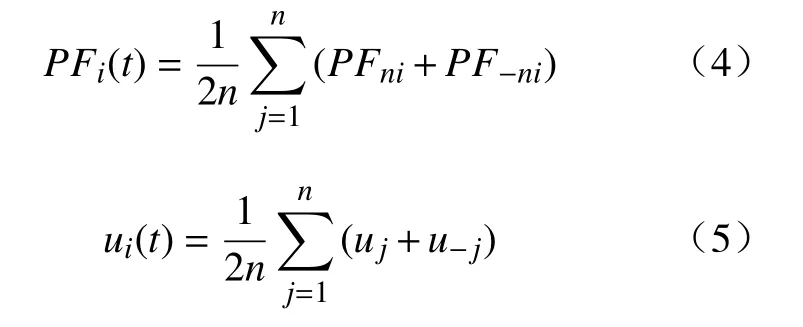
根据多尺度排列熵法对PF分量进行处理，基本原理如下：

设长度为N的时间序列：X={x1，x2，…，xN}，对其进行粗粒化处理，得到序列yj(s)，即

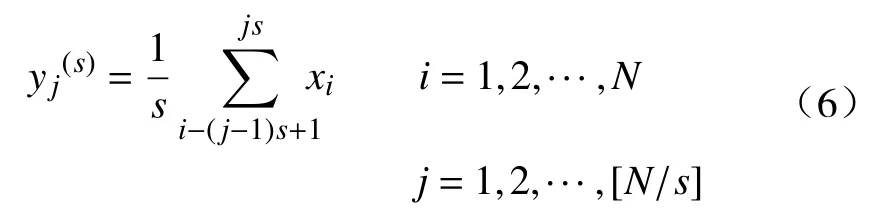
式中：yj(s)为粗粒化序列；s为尺度因子；[N/s]表示对N/s取整。当尺度因子s=1时，粗粒化序列即为原始序列。

MPE计算步骤如下：

1）对时间序列进行粗粒化处理及相空间重构；

2）将重构后的分量进行升序排列，计算每一种符号序列出现的概率；

3）计算每一个粗粒化序列的排列熵，并进行归一化处理得到MPE均值。

本文通过计算MPE的均值选取PF敏感特征低频分量并进行包络分析，识别故障特征。

1.3 高频信号故障特征提取

最大相关峭度解卷积算法(MCKD)以相关峭度最大化为解卷积滤波系数寻优目标函数，可达到突出信号冲击成分的目的。相关峭度表达式为

式中：yn为周期冲击故障信号，为解卷积周期；N为原输入信号的采样点数；M为移位数，一般取 1～7[17]。

振动信号中周期性冲击成分与环境噪声en及传递路径之间为一种卷积关系，解卷积滤波器可使冲击成分更加突显。假设hn为冲击信号，yn为通过周围环境及传输路径时的衰减响应，ch为分解得到的高频分量，则有[18]

MCKD法通过解卷积从卷积信号中还原被传递路径中卷积成分干扰的原始信号，即

式中：f为滤波器系数，f= [f1,f2,···,fL]T；L为滤波器长度。

最大相关峭度则为

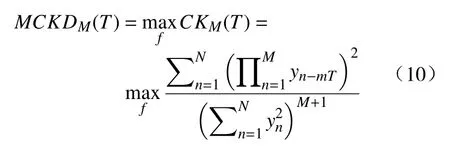
当MCKDM(T)最大时，则有

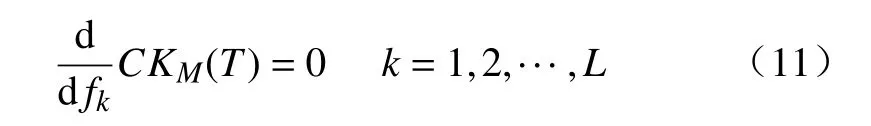
对式（11）求解，可得到滤波器系数矩阵，即

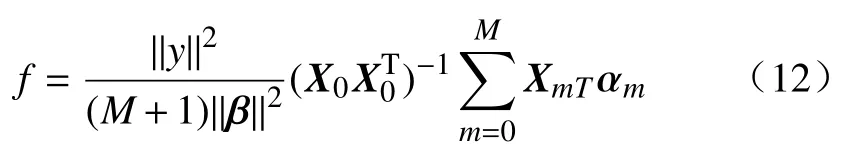
其中：

将滤波器系数矩阵代入式（9），对高频分量ch处理得到解卷积信号，即冲击故障信号yn。

故障会破坏系统的正常状态，使得系统信号频带上谱熵值发生变化[19]。减速器正常运行时，信号的能量波动为常值，谱熵值最大；当减速器出现故障时，信号的能量波动改变，谱熵值最小。利用信号时、频域内的谱熵值可对能量的波动进行度量[20]。谱熵值的计算原理为：

对于长度为L离散时域信号x(n)，n∈[0，L]，在频带区间[f−Δf/2，f+Δf/2]内分别利用希尔伯特变换H(·)，得到时域信号的平方包络SEx(n；f，Δf)：

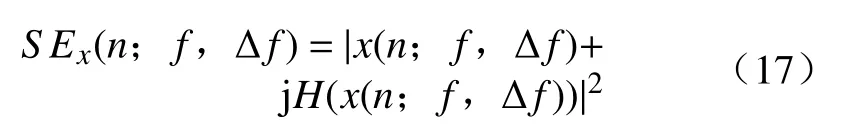
对时域信号的平方包络SEx(n；f，Δf)进行傅里叶变换F(·)，得到频带区间内的频域平方包络谱，即

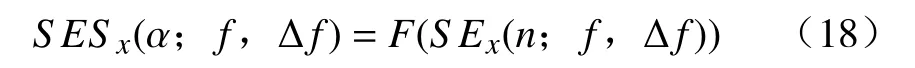
式中α为循环频率。

对式（17）、式（18）作均值运算可得到时域、频域内信号的谱负熵值：

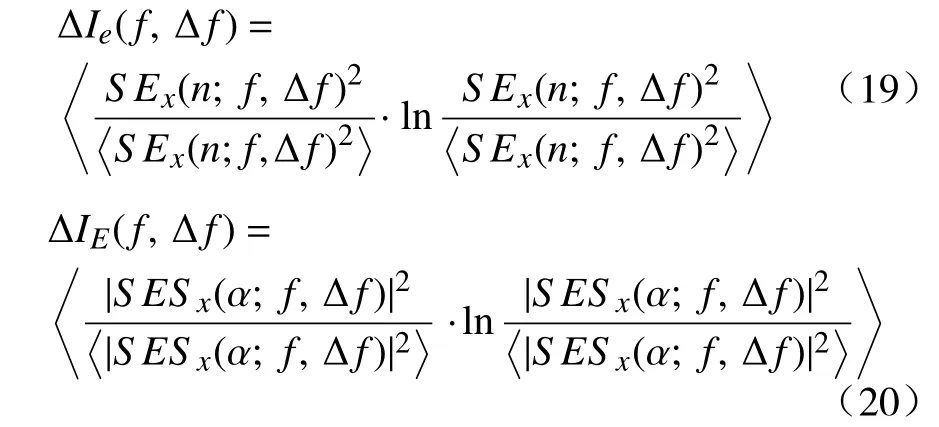
由于故障信号中往往混杂着噪声信号，通过对式（19）、式（20）取均值，即可得到频带区间内信号的平均谱负熵值，即

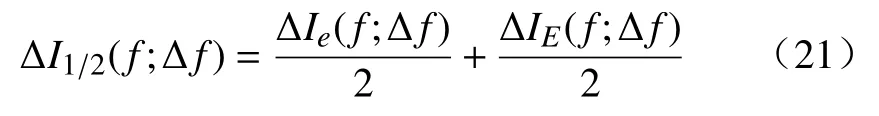
由平均谱负熵值包络成的信息图即为平均信息图（Average infogram），利用平均信息图即可确定信号的共振频带。

2 分段融合复合故障诊断流程

利用分频融合方法对矿用提升机减速器进行复合故障诊断，其流程如图1所示。

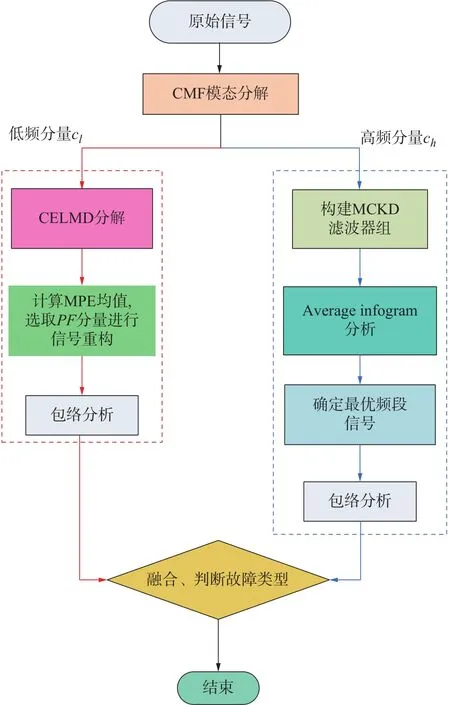
图1 分频融合复合故障诊断流程

诊断过程如下：

1）对原始故障信号进行CMF分解，得到低频模态分量cl和高频模态分量ch。

2）将低频模态分量cl进行CELMD分解，计算MPE，选取PF分量并进行信号重构。

3）对重构后的低频模态分量进行包络分析，并与减速器齿轮的理论故障频率进行对比。

4）利用公式Ti=fs/fi、To=fs/fo、Tb=fs/fb分别计算滚动轴承故障特征的解卷积周期，其中，fs为采样频率，fi、fo、fb分别为内圈、外圈和滚动体故障特征的理论计算频率。得到解卷积周期后设定滤波器长度，并构建与故障冲击相匹配的MCKD滤波器组，将高频模态分量ch进行滤波处理后分别计算各故障分量的平均谱负熵值，得到关于频带分量的Average infogram图，确定最优滤波频段信号。

5）对最优滤波频段信号进行包络分析，并与理论故障频率进行对比。

6）根据低频、高频的包络分析结果确定矿用提升机减速器的复合故障类型。

3 试验验证

针对矿用提升机减速器的工况特性，搭建矿用提升机减速器故障模拟试验台如图2所示。

图2 矿用提升机减速器故障模拟试验台

矿用提升机减速器故障模拟试验台中选用的滚动轴承型号为 GB/T 276−2013−6206，选用的齿轮参数如表1所示。

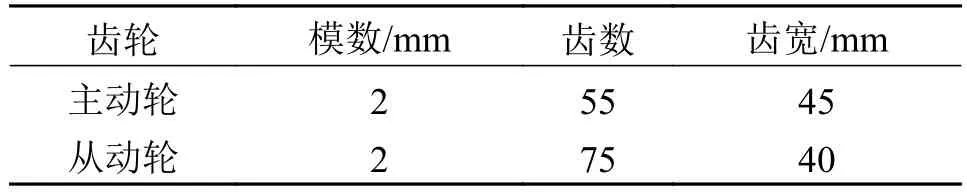
表1 齿轮参数

矿井检修数据表明：矿用提升机减速器主要故障为由齿轮、轴承组合成的复合故障。其中齿轮故障类型主要为磨损、裂纹和断齿，轴承故障类型主要为内圈故障、外圈故障和滚动体故障，如图3和图4所示。

图3 齿轮故障特征

图4 轴承故障特征

为验证矿井提升机减速器复合故障的分段融合诊断方法的有效性，以典型输出轴齿轮裂纹和轴承内圈裂纹作为复合故障形式进行实验分析。设定实验台额定负载为5 Nm、转速为450 r/min，由三相交流电机驱动实验台传动系统，通过变频装置调整输入轴转速，由磁粉制动器、载荷控制器及扭矩传感器构成负载系统。实验测得该工况下减速器故障信号时域、频域波形如图5所示。

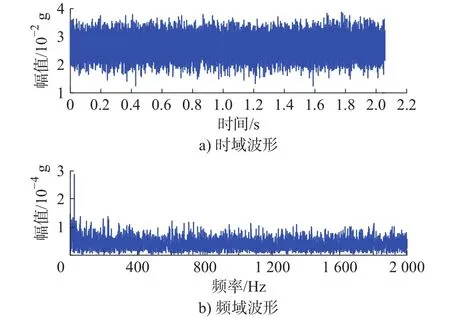
图5 减速器故障信号时域、频域波形

由图5可知：故障信号中杂乱干扰频率成分较多，使得特征频率成分不突出，无法据此直接判断故障类型。采用文中所提分段融合故障诊断方法对此故障信号进行处理分析，以啮合频率的2倍频为界利用CMF分解即可得到cl、ch分量，如图6所示。

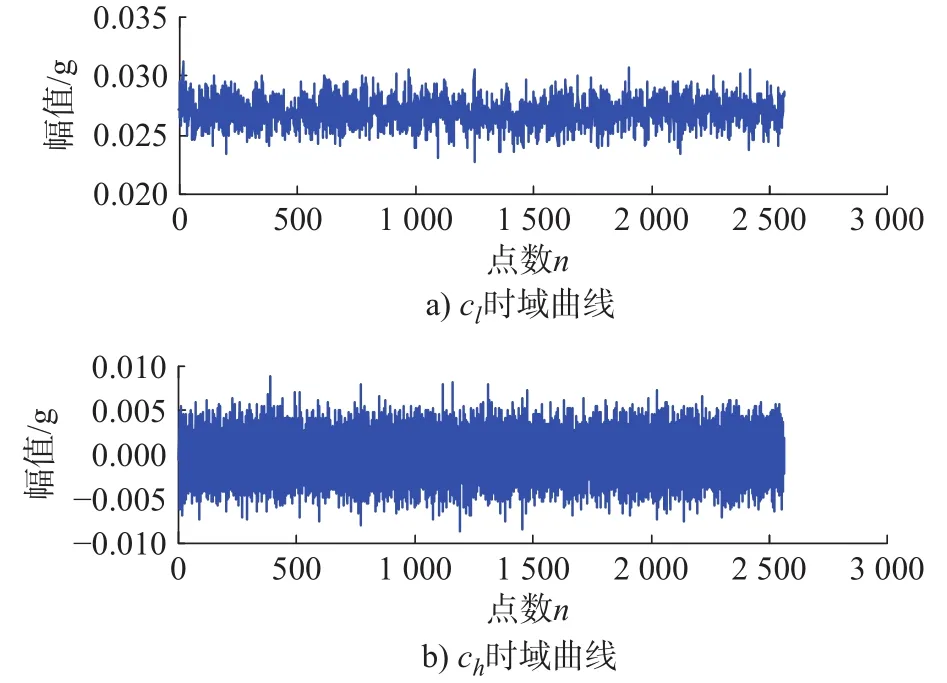
图6 故障信号 CMF 分解波形

对于低频分量cl，通过设置噪声标准差Nstd为0.5、集合次数NE为100，经CELMD分解获得8个PF分量信号，如图7所示。

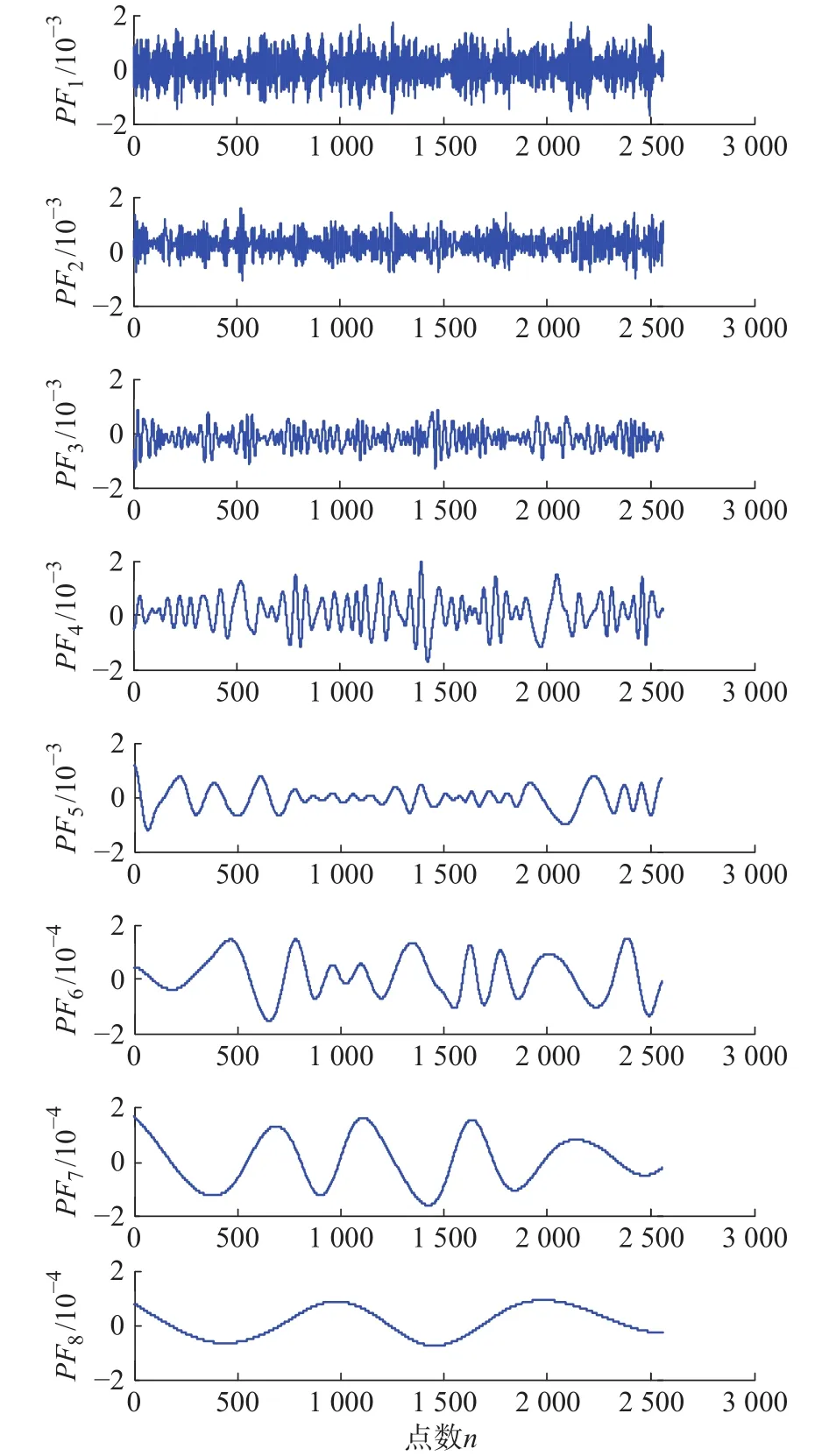
图7 低频分量 CELMD 分解

对CELMD分解后的各PF分量进行MPE计算，得到对应的排列熵均值如图8所示。

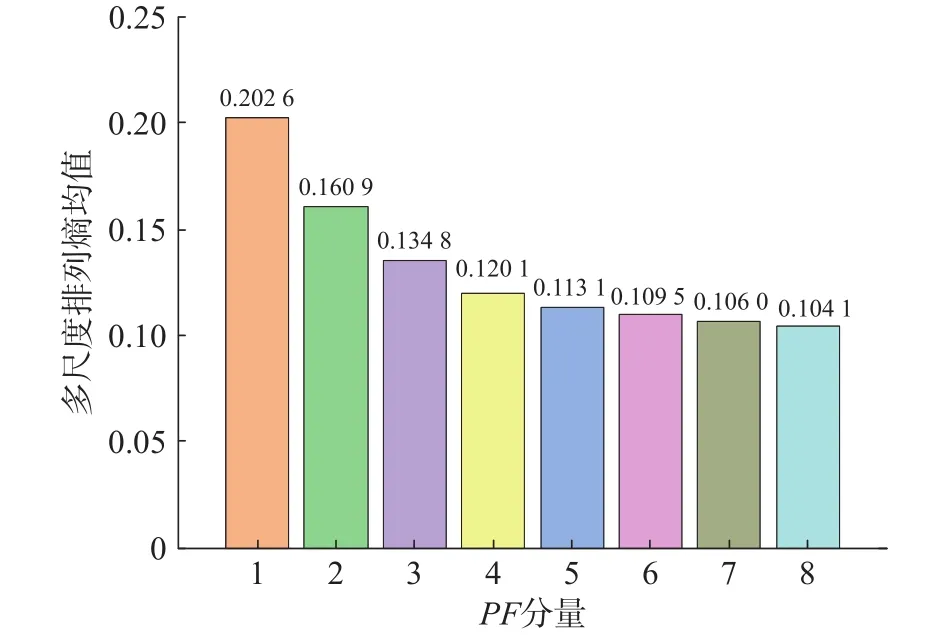
图8 各 PF 分量的 MPE 均值

由图8可知：前3项MPE均值分别为0.2026、0.1609、0.1348，区分度较为明显，敏感成分突出，可以判定前3项PF分量包含了主要故障信息。以此对低频信号重构并进行包络分析，得到其频谱图及包络图，如图9所示。

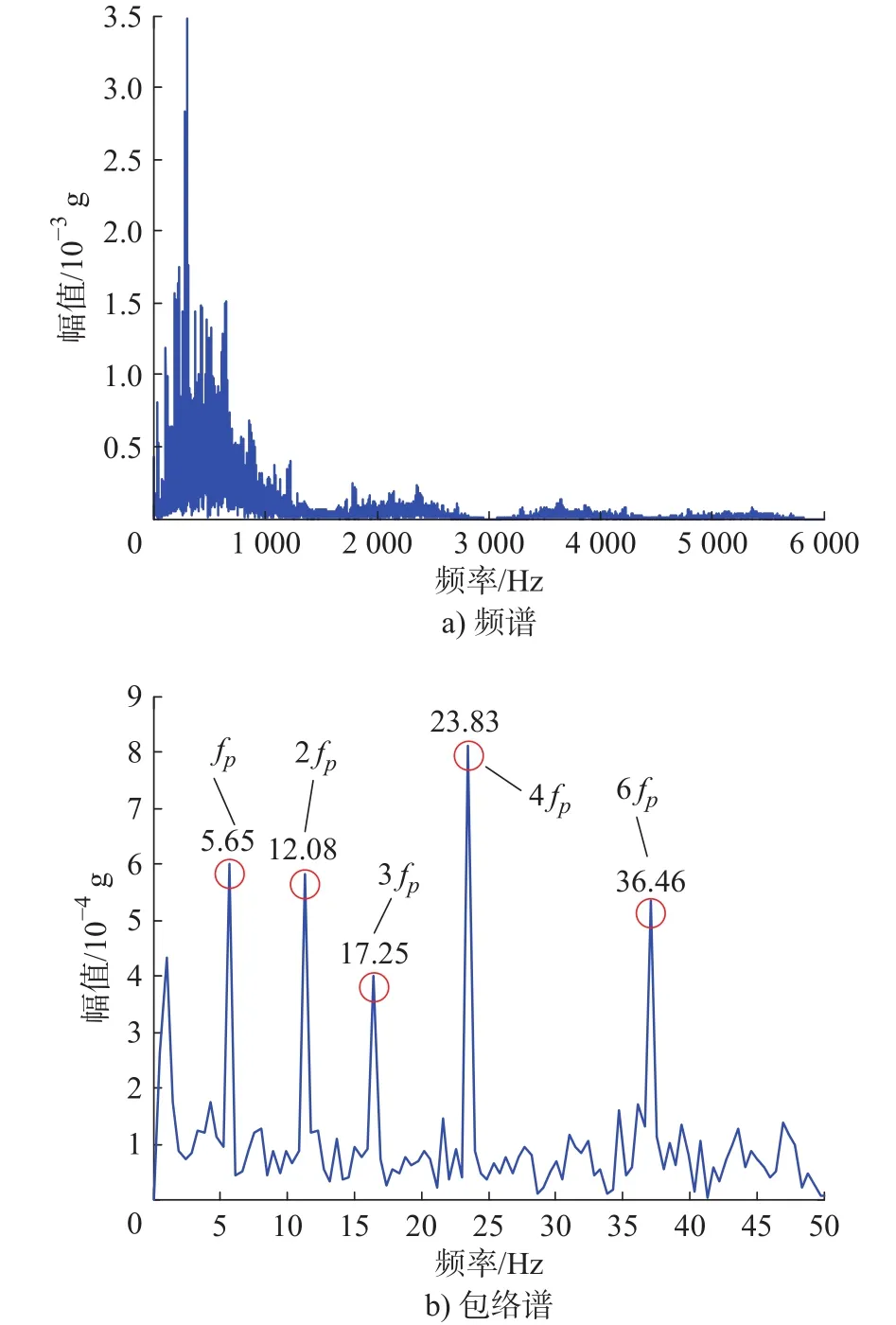
图9 MPE 重构后的低频分量波形

由图9可知：故障信号突出频率幅值成分明显，fp、2fp、3fp、4fp、6fp分别为5.65 Hz、12.08 Hz、17.25 Hz、23.83 Hz、36.46 Hz。而减速器输出轴齿轮裂纹故障特征理论计算频率fp= 5.5 Hz。各阶倍频与齿轮的理论计算频率基本吻合，因此可以判定减速器系统中输出轴齿轮存在裂纹故障。

以最大相关峭度为目标，设定最佳滤波器组长度L=100，采样频率fs= 12000 Hz，轴承故障特征对应的滤波器解卷积周期为：内圈Ti= 402，外圈To=609，滚动体Tb= 465。对 CMF 分解所得高频分量ch进行MCKD处理，得到不同故障频率解卷积滤波后的时域信号并进行Average infogram分析，结果如图10所示。由图10可知：轴承3种故障类型的最佳共振频率分别为 2125 Hz、5000 Hz、4969 Hz。对获得的最佳频带区域进行滤波运算，通过包络分析剥离信号中的故障冲击成分，结果如图11所示。

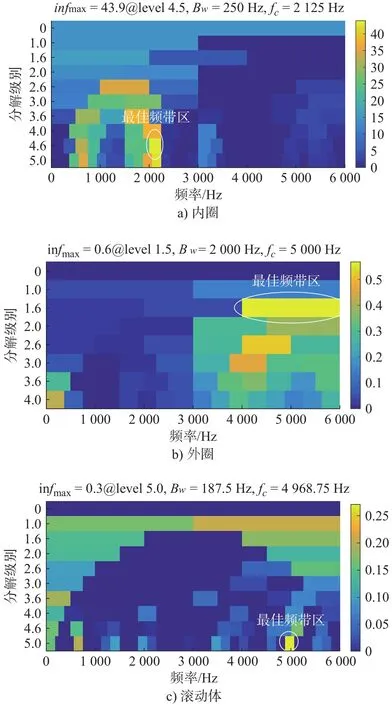
图10 轴承故障信号平均信息图

由图11可知：滚动轴承内圈故障的突出频率分别为29.5 Hz、58.6 Hz、88.3 Hz、121.2 Hz、152.9 Hz、210.2 Hz；外圈故障的突出频率分别为 26.6 Hz、83.7 Hz、140.1 Hz、203.4 Hz、261.0 Hz；滚动体故障的突出频率分别为 23.6 Hz、40.2 Hz、56.9 Hz、76.7 Hz。滚动轴承内圈、外圈及滚动体故障特征理论计算频率分别为fi= 29.8 Hz、fo= 19.7 Hz、fb=25.8 Hz。对比可知，滚动轴承内圈故障突出频率与其特征频率的fi、2fi、3fi、4fi、5fi和 7fi基本吻合；而外圈故障突出频率和滚动体故障突出频率与其特征频率相差较大，均未得到对应的故障特征成分，因此可以判定减速器系统中滚动轴承存在内圈故障。

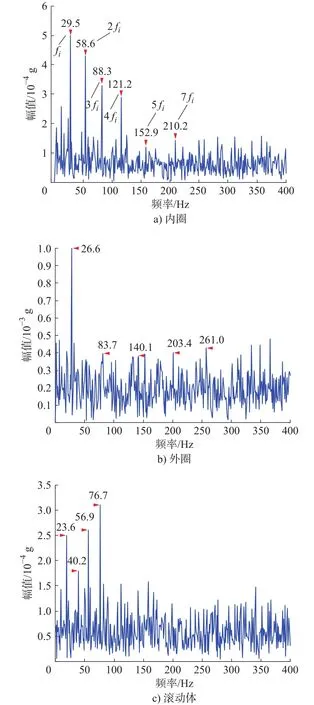
图11 最佳频带滤波后信号的包络谱

根据低频、高频模态分量分段融合诊断结果判定：矿井提升机减速器复合故障类型为齿轮裂纹和滚动轴承内圈故障，与实际故障情况一致，分段融合方法用于矿井提升机减速器复合故障诊断可行。

4 结论

1）对低频啮合分量进行CELMD降噪处理，应用MPE方法增强信号中的微弱冲击故障特征，准确提取故障特征的敏感PF分量，提高了故障特征的辨识效果。

2）设计MCKD逆滤波器组，对高频共振分量进行滤波处理，提取与故障特征频率相关的周期性冲击成分，并结合Average Infogram进行包络分析，实现了复合故障的有效分离，避免了因频带信息选择不全造成的漏诊和误诊问题。

3）提出的分段融合故障诊断方法能够有效对强弱共生及噪声干扰的振动信号进行降噪、分解，实现了矿用提升机减速器复合故障的特征提取及准确诊断，为工况环境复杂的大型低速传动设备故障诊断问题的研究提供参考。