基于APD与PIN接收机的UWOC系统误码率性能优化研究

史宏强，李岳衡，黄 平，谭跃跃，刘陕陕，居美艳

（河海大学计算机与信息学院,江苏南京 211100）

1 引言

近年来随着无线通信技术的快速发展和各国对海洋资源探索的日渐深入，人们对水下高速、可靠无线通信的需求越来越迫切. 传统水下声波通信由于其低载频以及存在多径扩展与多普勒效应而使得通信的传输速率和传输质量皆无法令人满意，而水下射频通信则受到传输频率以及损耗等非可控因素的影响，继而导致接收信号出现大幅度的波动［1，2］. 在此背景之下，水下无线光通信（Underwater Wireless Optical Communication，UWOC）以其速率高、延迟低、保密性强等巨大优势而吸引了众多科研工作者的关注，并逐渐成为无线通信领域新的研究热点［3，4］.

鉴于UWOC 不同于传统陆地自由空间中大气激光通信易受云雾和湍流的双重影响［5］，以及室内可见光通信主要遭受路径损耗的传输特性，有必要首先通过理论分析或者实验仿真的方式获得水下无线光通信信道的传输特征［6，7］. 其中基于蒙特卡洛（Monte Carlo）方法的计算机仿真，以其模拟过程和结果能有效避免直接求解复杂的光辐射传输方程及数值准确性，一经提出即成为相关领域开展研究并据此获取UWOC 系统信道特性的有效手段［8，9］. 不过，仅仅获得有关典型海洋通信环境下的信道传输特性模拟数值是不够的，因为后续诸如系统误码率（Bit Error Rate，BER）、中断概率等UWOC 系统性能指标的评估，尚需采用具闭型数学表达的信道衰落模型来加以定性刻画，以方便理论层面的推导与分析. 文献［10～12］中所采用的信道路径损耗模型及性能分析基本上都是基于理想单指数衰落模式进行的，没有考虑真实海洋环境，比如清澈海洋等不同水质下的海水吸收与散射效应对信道衰落的真实作用. 文献［13，14］虽然考虑了散射对信道衰落的影响而对单指数衰落模型进行了修正，提出了所谓的双指数（Double Exponential，DE）路径损耗拟合函数，但其为分析问题简便，所提出的信道衰落模型均没有对接收机可能倾斜而导致的指向损耗这一重要因素进行分析与描述，即认为收发机是轴对准布置的. 不过在实际海洋环境中，由于有海洋湍流、海底地震等水下活动的存在而不可避免地使得收发机难以保持理想的互相对准的状态，因此该信道模型存在一定的缺陷.

此外，研究结果还显示，UWOC 系统的接收机采用何种光电二极管（PhotoDiode，PD）作为检测单元对系统的信号建模也有非常重大的影响［15］. 而上述文献基本上仅考虑一种简单的PIN（Positive-Intrinsic-Negative）光电管的接收模式，虽然方便系统建模，但导致问题分析不够完善与全面. 文献［16］则分别考虑采用PIN、APD（Avalanche PhotoDiode）和PMT（Photo-Multiplier Tube）作为接收PD 时，太阳背景噪声对点对点UWOC 链路性能的潜在影响，并通过数值仿真研究了不同接收机参数下的系统误码率性能.Xu 等提出并经实验验证了一种基于简单红光镭射二极管的宽带UWOC 系统，并在高阶调制下研究了使系统在PIN 和APD 两种接收场景下获取高速数据传输的方案［17］.Das等则探讨了接收机分别采用PIN 和APD 两种PD 时，UWOC 系统于典型水质下的最大传输距离［18］. 文献［16～18］虽然给出了不同PD 接收模式下的UWOC 系统BER 仿真曲线，但其信道模型中依旧没有考虑指向误差的影响，基于此影响的有关UWOC 系统误码率性能的优化分析自然亦无从谈起.

为此，本文首先提出并经数值仿真验证了一种含指向误差的UWOC系统路径损耗模型，并基于此进一步提出了一种采用APD 和PIN 接收机时的UWOC 系统BER优化分析方法，即通过对指向误差与BER之间的关联进行建模，采用数学优化方法求解最优指向误差角进而提升系统的BER性能. 本文主要贡献总结如下.

（1）区别于文献［10～14，16～18］，本文所提出的信道路径损耗模型考虑了由接收机倾斜而引起的指向误差这一重要因素的影响，并且从仿真层面验证了含指向误差的DE信道衰落模型的准确性和有效性. 这种通过仿真验证信道模型的方法在文献［13，14］中亦是如此加以运用的.

（2）文献［16～18］仅展示了不同PD 接收场景下误码率性能的数值仿真结果，并未针对某一PD 接收场景给出系统BER 的理论闭型表达，未对UWOC 系统误码率性能进行更深层次的研究. 本文则针对APD 与PIN两种PD 接收场景，分别给出了其所对应的系统BER 闭型表达的详细推导流程，对指向误差与BER 之间的关联进行建模，并以最小化系统BER 为数学优化目标，证明该优化问题实际上是一关于接收机指向误差角的简单凸优化问题，故而通过优化指向误差角即能显著提升整个UWOC系统的误码性能.

2 系统模型

如图1 所示建立空间直角坐标系：以光源O为原点，接收机在半径为12.6 m 的1/4 圆面上移动（由对称性及简化问题分析起见，本文仅考虑图示1/4 圆面并设其所在象限为第一象限），光源距圆面的垂直距离为19.25 m，d为光源至接收机之间的距离，且光源和接收机的坐标分别为[0，0，0]和[x0，y0，z0]，接收机的视场角FOV（Field of View）=180°. 需说明的一点是，之所以接收圆平面的半径和光源至接收平面的距离定为图示的数值，是因为本文后续所提带指向误差的DE 路径损耗模型的系数确定需要这些具体的参数，即在图示参数下获得路径损耗模型的系数. 设光源波束始终对准接收机，记接收机指向光源的向量为Vor，Vn为垂直于接收机平面的单位法向量，接收机的偏转角为θ，法线Vn与指向向量Vor之间的夹角设为β（即指向误差角）. 为进一步简化分析，设z轴、Vor和Vn三线共面，如此它们之间所构成的夹角间的相互关系可用图1 中右上角的子图加以列示. 此外，忽略接收机平面的大小对Vor的影响，则由图1 可以看出，一旦接收机位置固定下来，Vor的指向将不随接收面的倾斜而发生改变，但Vn的指向显然会随接收面的倾斜而不断变化，也即Vn和Vor之间的指向夹角β将发生改变，它应该是变量θ的一元函数.

假设图1所示UWOC系统位于清澈海洋水质环境，发射端采用强度调制传输信号而接收端采取直接检测进行统计判决，在考虑水下无线光通信信道衰落，以及考虑APD 和PIN两种接收PD因存在不同强度的“光-电散弹电流”和“热噪声电流”分布特性从而导致不同背景噪声的基础之上［19，20］，接收输出电流信号模型根据接收机采用PD的不同而有如下两种类型的表达方式：

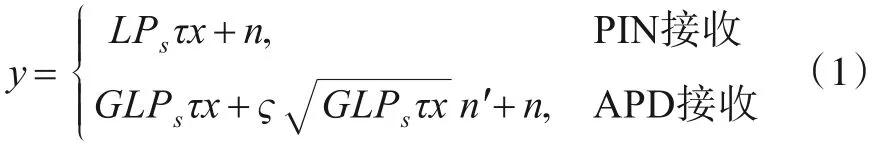
其中，L为信道衰落；τ=ηq/hv 是光电转换系数，η是量子效率，h是普朗克常数，v是海水中光波的频率，q是电子电荷；Ps是信号发射功率；x∈{0，1}是开关键控（OOK）强度调制发射符号；n是接收机背景噪声，不论接收机采用PIN 还是APD 型PD，n都可以表示为电阻的热噪声，故可模拟为均值为零、方差为σ2的高斯白噪声，其噪声功率（方差）值为

其中，K 是波尔兹曼常数，T是卡尔文温度，B是滤波器带宽，R为负载电阻阻值，F是系统噪声系数. 而当接收端采用APD 时，系统噪声除背景热噪声n之外，还含有与接收平均电流强度成正比的散弹噪声项，其中G为APD 的平均增益，ς为一与参量有关的常数，其值大小为，其中F1=ξG+(2-1/G) (1-ξ)为额外噪声因子，ξ为离子化率［20］；高斯白噪声n'～N(0，1)与热噪声项n相互独立.

对于式（1）中的信道衰落L，本文采用含指向误差的DE 路径损耗模型加以刻画：两个指数项不仅可以分别描绘多阶散射和低阶散射或直达径这两种情形下的信道损失，指向误差项更可以体现接收机与入射光线存在非对准情况下的性能损失，因而能更全面体现UWOC 系统几何参数对系统信道衰落的影响. 含指向误差的DE信道衰落模型定义为

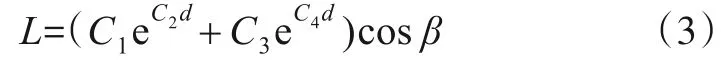
其中C1，C2，C3，C4为根据Monte Carlo 仿真数据获得的清澈海洋水质下的拟合系数；d为光源至接收机之间的距离；β为入射光线与倾斜的接收平面法线之间的夹角，即指向误差或指向损耗.

根据图1，由空间解析几何的相关知识可知，指向误差cosβ的计算为

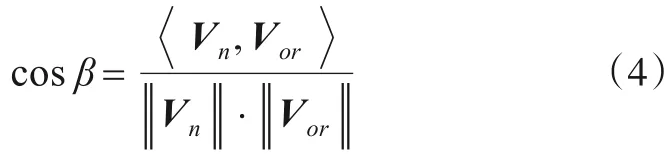
上式中单位矢量Vn=［sinθcosφ，sinθsinφ，cosθ］，Vor=[(0-x0)，(0-y0)，(0-z0)]，代入式（4）化简后有

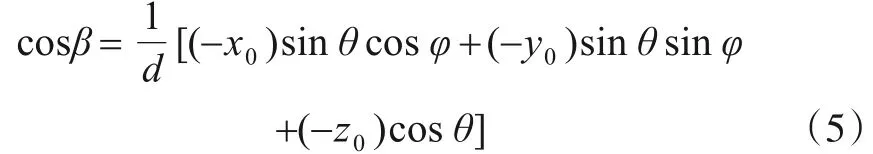
其中θ等于矢量Vn与垂直方向的夹角，也即接收机平面的水平倾斜角，φ是Vn在水平方向投影后与x轴正方向形成的方位角. 事实上，由于Vn，Vor，z三向量共面，φ完全由接收机在x-y平面上的坐标所决定，如下图2 所示. 从图中不难看出，方位角φ可以表示为

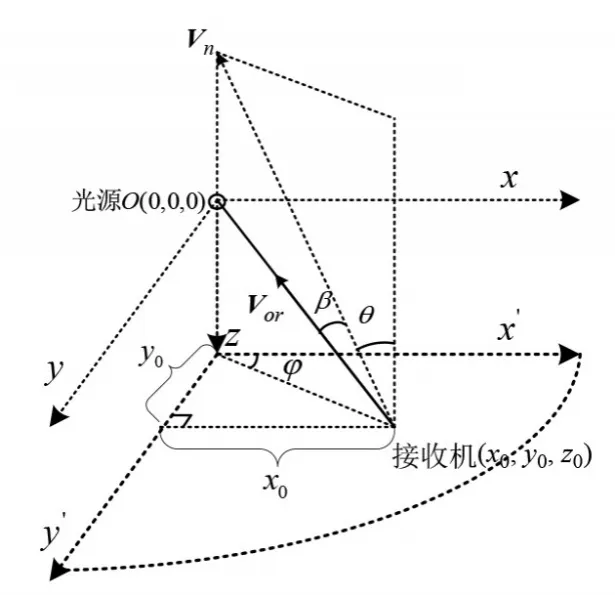
图2 接收机平面法线在x-y面第一象限上的投影

3 接收机误比特率理论公式的推导

UWOC 系统根据接收机采用的PD 类型的不同而分成APD 接收和PIN 接收这两大类. 由于APD 和PIN对接收噪声贡献的不同，当接收端采用最大似然检测进行符号判决时会存在不同判决门限的差异，故而需对这两种接收机的理论误码性能分别加以分析.

3.1 APD接收

当接收机采用APD 雪崩二极管时，接收端占主导地位的噪声源包括散弹噪声以及电流热噪声［20］. 根据式（1），此时输出电流y的条件概率密度函数可以写成

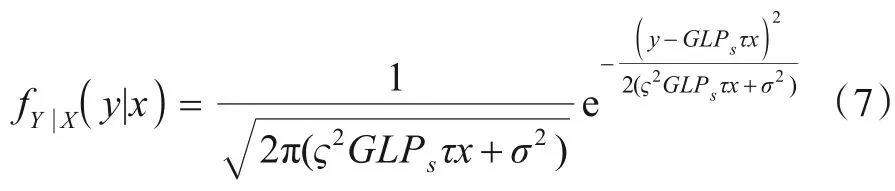
结合式（1），当OOK 调制为“关”的状态时，不难求出此

时的输出电流y的均值为

方差为

同理，可求出当OOK 调制为“开”的状态时，输出电流y的均值为

方差为

由于发送不同OOK 符号时的背景噪声大小不同，当接收机采用最大似然准则进行判决时，其最佳判决门限电流值需根据优化理论计算获得，根据文献［15］的推导结果有

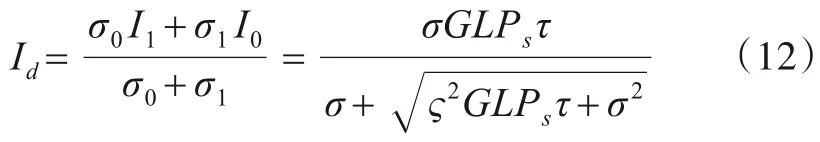
有了判决门限，发射机发送OOK 符号1 而接收机错判为0的概率即可计算为

同理，发送符号0而错判为1的概率Pr( 1|0 )为

其中erfc(x) =e-t2dt为互补误差函数. 综上，在接收机采用APD 型二极管且等概发送OOK 符号的情况下，系统平均BER为

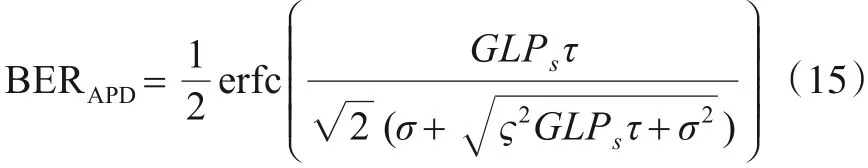
3.2 PIN接收

当接收机采用PIN型光电二极管时，此时噪声源主要为电流热噪声［20］. 由式（1）可知，输出电流信号y的条件概率密度函数fY|X(y|x)可以写成

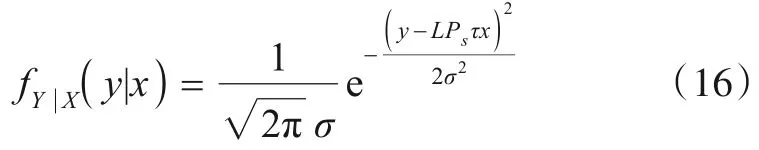
则采用最大似然检测，n为加性Gauss白噪声时，不难得到最优判决门限为LPsτ/2. 根据式（16），发射机发送OOK符号1而接收机错判为0的概率为

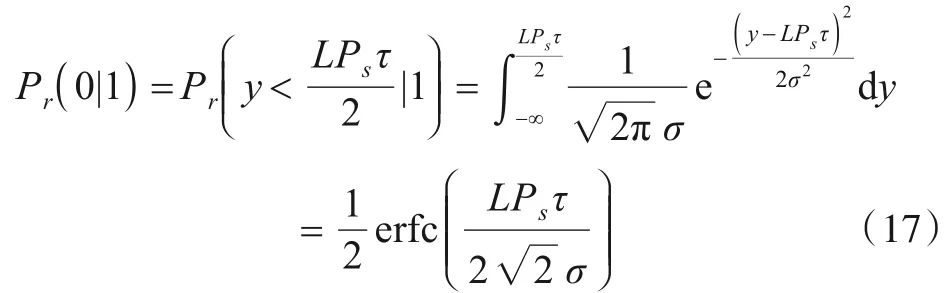
同理有

因此，最终的BER可以写成

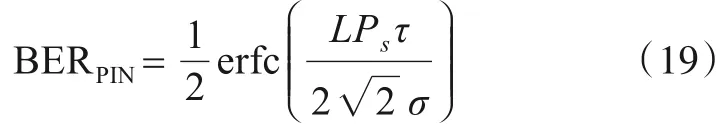
4 优化问题的提出与求解

从上述推导所得的UWOC 系统含指向误差的BER表达式可以看出，当链路距离d定下来之后，该BER 是一个有关光源和接收机之间指向误差β的、或者说关于接收机平面与水平x-y平面形成的倾斜角θ的一元函数，改变倾斜角θ将有可能获得该距离处系统的最优BER，因此上述分析转化为一个数学优化问题. 为此，首先给出BER 优化求解问题的数学描述，在此基础上再进一步证明该优化问题是一个简单的凸优化问题，从而获得最优倾斜角和相应BER的理论求解.

4.1 UWOC系统BER优化问题的描述

以最小化图1 所示UWOC 系统接收机BER 值为优化目标，考虑接收机平面倾斜的有效范围，该优化问题可以表示为

4.2 问题的求解

4.2.1 APD接收机

当接收机采用APD型PD时，对BERAPD求关于L的一阶导数，经处理简化后不难得到如下表达

这说明APD接收机的BER是路径损耗L的单调递减函数；当L取极大值时其所对应的BER最小.

4.2.2 PIN接收机

类似地，当接收机为PIN型PD时，由互补误差函数随自变量单调下降的性质可知，此时UWOC 系统的BER亦随L的增加而单调下降，也即有

综上所述，不论采用何种PD，原优化问题（20）皆可等价于如下优化问题：

将式（5）代入式（3），可得含待优化变量θ的路径损耗L的表达式为

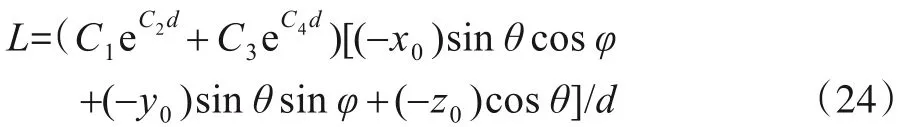
不难求出L关于θ的二阶导数=-L≤0，这表明目标函数L是关于倾斜角θ的上凸函数；也就是说，存在某一θ值以令路径损耗L达到最大，即令系统BER达到最小. 由于式（23）中的目标函数L关于θ是凸的，定义域也属于凸集合，因此它是一个凸优化问题［21］.

由L关于θ的一阶导数可求得令系统BER 达到最小值的最优倾斜角θ0为

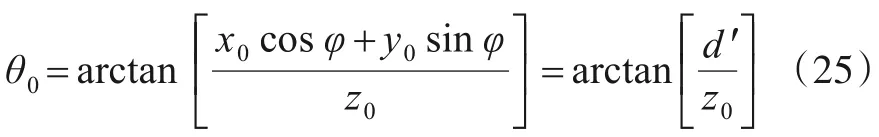
其中d'为接收机坐标点与光源在x-y平面投影的连线距离. 结合图2 和式（25）不难看出，获得最优倾斜角θ0时的指向误差角β=0°，这说明所谓的最优倾斜即接收机平面的法向向量和入射光线完全对准的情形；换句话说，就是当接收机在水平圆平面上移动时，若要获得最优的BER，需要倾斜接收机将其平面法线和入射光线重合即可.

5 数值仿真与分析

在本节中，首先通过蒙特卡洛数值仿真（Monte Carlo Numerical Simulation，MCNS）来验证，采用含指向误差的DE 衰落信道模型来表征清澈海洋水质下系统信道特性的合理性，并获得该表达式的各个拟合系数.为此，首先需要搭建基于MCNS 的UWOC 系统信道特性仿真平台，其相关物理实现流程与数学原理的介绍参见文献［8］. 随后再通过仿真来验证上述推导的有关UWOC 系统误码率理论表达的正确性. 此外，也将研究通过倾斜接收机平面来克服指向误差cosβ，从而提升UWOC 系统整体误码率性能的可行性. 上述仿真平台的搭建及BER 优化仿真均借助MATLAB 软件加以完成.

5.1 含指向误差的双指数信道衰落模型仿真验证

假设系统处于清澈海洋水质；此外，又假设收发机是轴对准的，即接收机位于发射光源的入射光轴上，且初始指向误差角β=0°，即接收平面的法线与入射光轴重合. 本文所述的含指向误差的信道衰落模型验证仿真包含以下两个步骤.

步骤1：UWOC 系统路径损耗MCNS 与拟合系数获取

当收发距离控制在10～30 m 之间变化以及指向误差β=0°的条件下，通过MCNS 记录接收光子的特性.不失一般性，假设单个光子的重量为1，每次发射的光子数为106，其他仿真参数详见表1. 仿真中，首先通过归一化接收功率得到接收强度关于d的变化曲线，即纯路径损耗曲线，如图3（a）中的圆点线所示. 随后，根据非线性最小二乘准则获取DE 函数拟合清澈海洋水质MCNS 路径损耗仿真数据的结果，如图3（a）中的实线所示，进而得到DE 函数的最优拟合系数，其系数值及对应的拟合误差详见表2. 从仿真结果可以看出，在收发机完全理想对准的情况下，即β=0°时，DE 函数能很好地拟合清澈海洋环境UWOC 系统的纯路径损耗.

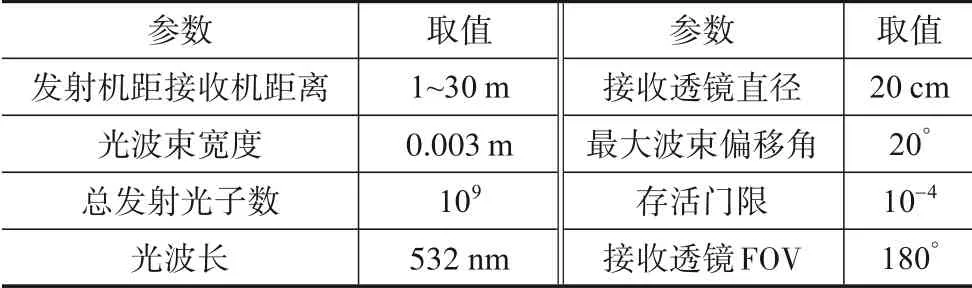
表1 MCNS主要参数

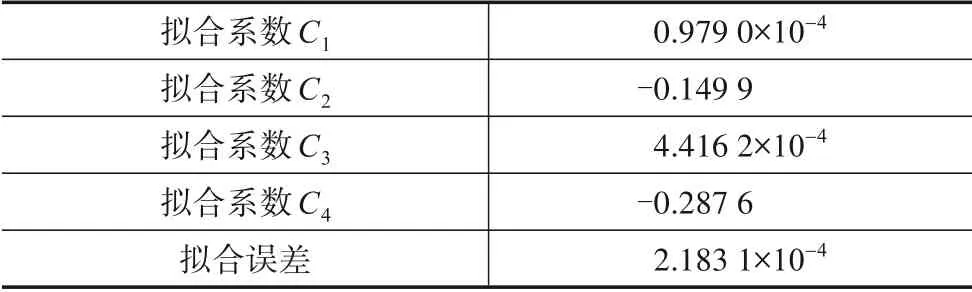
表2 10～30 m清澈海洋水质DE函数拟合系数及拟合误差

步骤2：含指向误差的DE路径损耗模型仿真验证

在步骤1所获得的DE损耗函数最优拟合系数的基础之上，分别固定收发机之间的距离d为10 m，15 m，20 m以及25 m，并且在0～90°的范围内变动指向误差角β，通过Monte Carlo仿真获取固定收发间距d时，归一化接收强度随指向误差角β的变化曲线，并与式（3）的理论计算值进行对比，以验证含指向误差的DE 函数路径损耗式（3）的合理性与有效性，二者间的对比结果如图3（b）中的子图所示. 从这些仿真图形可以直观地发现：在一定的通信链路距离之内，含指向误差的DE函数完全可以通过双指数项来体现清澈海洋水质的纯路径损耗部分，且可以通过指向误差项cosβ来反映接收机因几何放置而导致的指向损耗，从而可以更加全面地表征UWOC系统的信道特性.

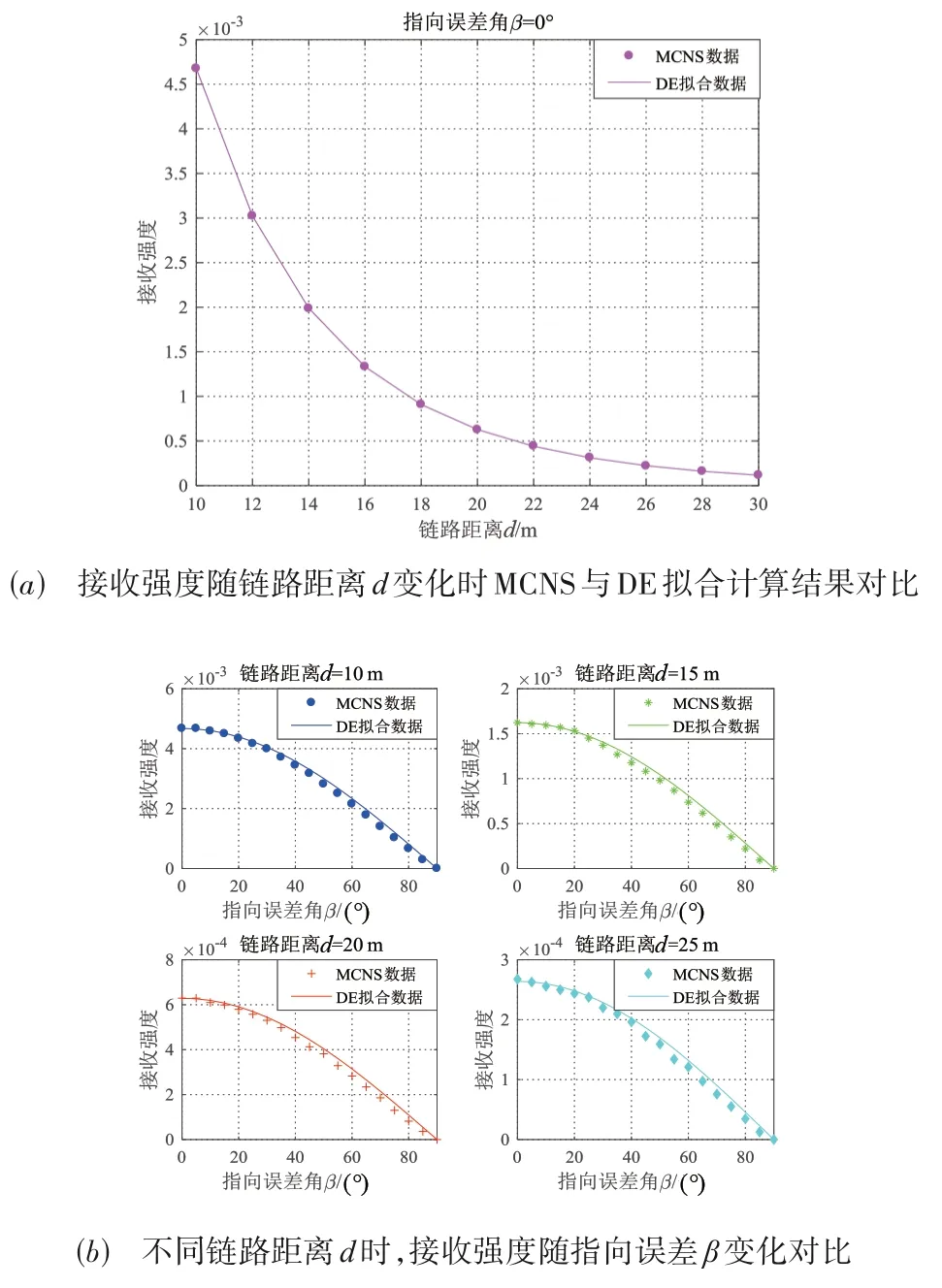
图3 MCNS与双指数拟合对比图

5.2 系统BER数值仿真与分析

本文所采用的适合UWOC 系统APD 和PIN 接收机BER 仿真的主要参数列于表3 所示，其典型取值参考了文献［20］. 为了有效显示二者之间的区别，除发射光功率之外，其余所有仿真参数的取值都是相同的.此外，为令两种接收机的BER 基本保持在一个数量级，APD 接收时系统的发射功率的选取比PIN 小了近一个数量级. 仿真中，接收机根据最大似然准则进行统计判决，此时的判决门限按照第3 节中所推导出的两种不同PD 接收场景下的最优判决电平值来分别进行设定.

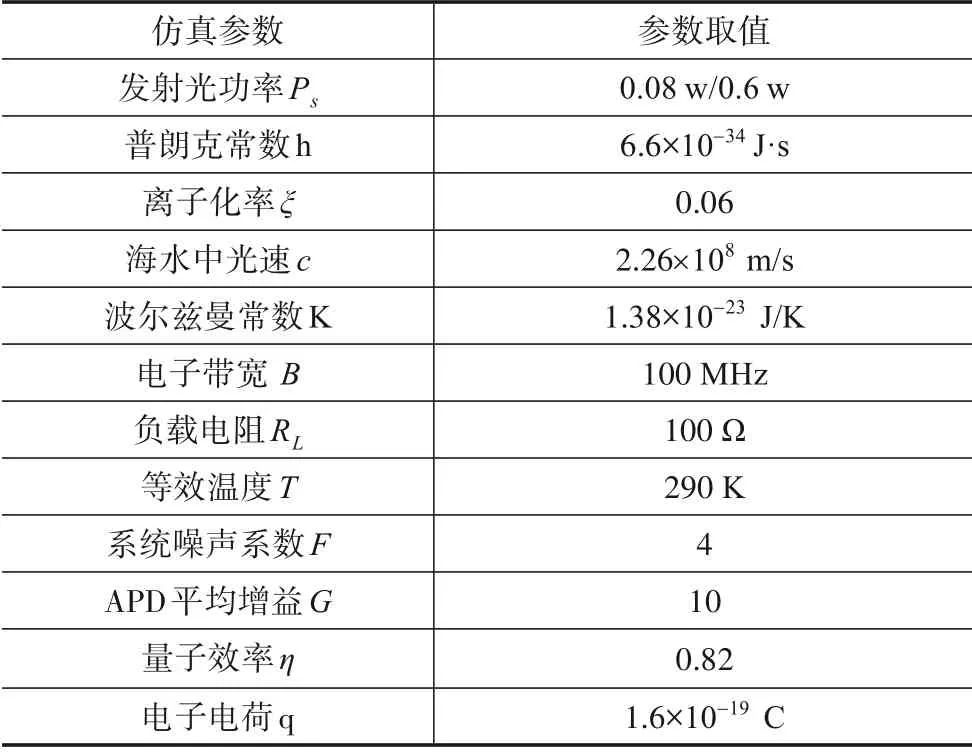
表3 APD/PIN接收机BER仿真主要参数

图4描绘的是在两种接收场景下，固定不同链路距离d时系统BER 关于倾斜角θ的变化情况. 结合图4（a）与图4（b），从整体上看，不论接收机是采用PIN还是APD型PD，两幅图的曲线变化趋势十分相似；即便考虑了选取较小的发射功率，APD 接收机的BER 依然明显小于PIN 接收机，这说明APD 接收机的性能要优于PIN接收机，这与前人的研究成果也是一致的［20］. 另外，从这两幅图的仿真结果还可以看出：只有连线距离为19.25 m 的曲线的BER 是关于倾斜角的单调递增函数，对于其余的d值曲线而言，BER总是随着倾斜程度的加剧先减小后增大，也即每条曲线都存在一个与最小BER 相对应的、该距离值下的最优倾斜角θ0；并且随着距离的增大，相应的最优倾斜角也渐渐变大，这意味着，当接收机离光源距离越远时，接收平面需要偏转更大的倾斜角以克服指向误差β带来的不利影响. 例如，当距离为19.25 m 时，此时接收机正好位于发射光源的正下方，当倾斜角为0°即接收机水平放置时，BER 最低，故该距离下的最优倾斜角为0°；当接收机逐渐远离发射光源，距离变为20.5 m 时，从图中不难看出此时的最优倾斜角增大为20°.

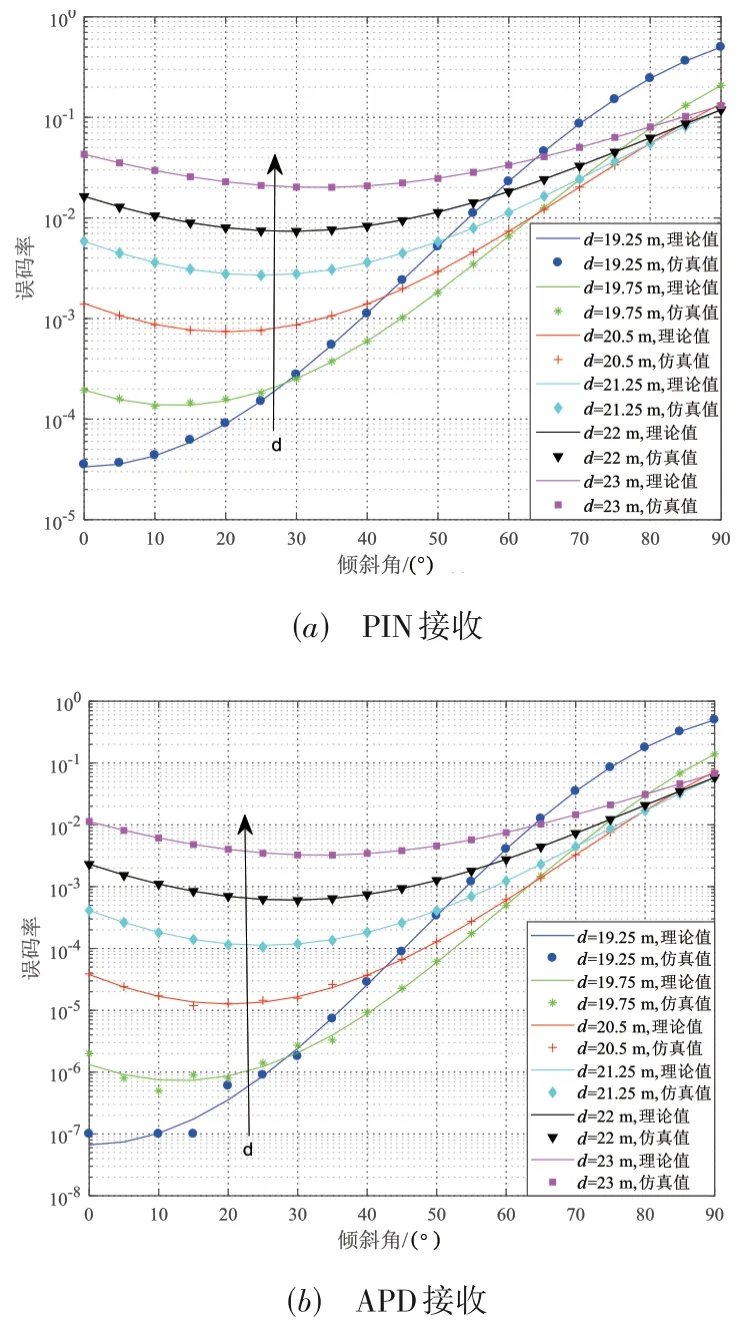
图4 不同链路距离下UWOC系统BER随接收机倾斜角变化曲线

另外，当倾斜角不超过25°时，固定倾斜角，BER 随传输距离的增大而呈数量级程度的恶化，这说明在倾斜角小于25°时，链路距离d较于指向误差β在路径损耗中起主导作用；而当倾斜角超过25°且逐渐增大时，不同距离d下的BER 曲线恶化的趋势逐渐减小. 这说明此时倾斜角θ导致的指向误差改善对路径损耗L的作用愈加明显. 从图中还可以看出，当收发距离较近时，BER 随接收机倾斜角的变化而波动较大，而距离较远时，倾斜角的改变对BER 的影响则比较有限. 综合而言，各传输距离d下的理论值和仿真值之间的误差可以忽略不计，从而验证了前述BER 理论表达式推导的正确性.

图5 描绘的是两种不同PD 场景下，分别固定接收机倾斜角θ为不同角度时，UWOC系统BER随链路距离d变化的理论值与仿真值之间的比较. 由图中数据可以看出，PIN 与APD 接收机的BER 曲线随d变化的规律大体上一致. 变化趋势上，除θ=0°曲线的BER 是关于距离d的单调递增函数外，其余固定倾斜角θ的BER 曲线呈现出随着距离d的变大先减小然后逐渐增大的趋势（θ=90°除外）. 也就是说，每条曲线都存在一个与最小BER 相对应的该倾斜角值下的最优配置距离，即当考虑接收机平面的倾斜度时，UWOC 系统BER 并不总是随着距离的拉长而增大，可以根据当前倾斜角下的最优配置距离来合理布置接收机，如此则系统BER 性能能够得到非常可观的改善. 并且随着倾斜角θ的变大，与之对应的最优距离也随之增大，这也从另一个侧面说明，随着收发间距d的增大，指向误差角β也随之增大，此时需要接收机平面偏转更大的倾斜角θ以消除其导致的不利影响. 对于较小倾斜角而言，收发机距离对BER 的影响十分剧烈；而对于较大倾斜角来说，收发距离对BER的影响幅度相对来说较小.

图5 接收机倾斜角一定时UWOC系统BER随距离d变化曲线

图6（a）和图6（b）为不倾斜PIN 接收机的接收平面以及最优倾斜PIN平面这两种情形下，UWOC系统BER随接收机在图1 所示水平圆面内放置坐标点的三维（3D）曲面分布图. 仿真中，光源固定位于光轴z的原点，接收机则可以在圆面上自由移动. 从图中数据可以看出，不论倾斜PIN 平面与否，接收机在边界圆周上的BER 都是最差的，而最小BER 则是当接收机位于光源正下方时获得. 这个结果是合理的，因为较长的传输距离会导致路径损耗增加进而引起性能下降. 另外，在x-y平面上以距光轴z固定距离为半径作圆的圆周上，BER也是相同的，这是因为此时接收机距光源的路径d相同. 再将该两子图进行对比后可以发现，在倾斜PIN 接收平面并获得最优倾斜角之后，整个x-y面（尤其是边界处）的BER大幅降低，比如，d=23 m时，未倾斜PIN平面的BER=0.043，而倾斜至最优角后的BER=0.020 1；这说明倾斜接收平面可以明显消除指向误差的影响，进而优化UWOC系统的BER性能.

图6（c）和图6（d）则为采用APD 型PD 时，原始不倾斜及最优倾斜接收平面时，UWOC 系统BER 关于接收机在x-y平面放置坐标的3D 误码率曲面图，所得结论与PIN 接收的情形基本类似：抛开发射功率对BER 的影响，APD 接收时，最优倾斜接收机平面后边界处的BER 相比未倾斜时的优化幅度比PIN 接收时更加明显. 例如d=23 m 时，未倾斜APD 平面的BER=0.011 3，而倾斜至最优角后的BER=0.003 2，优化幅度为71.68%，而相同距离PIN接收时优化幅度则是53.26%.

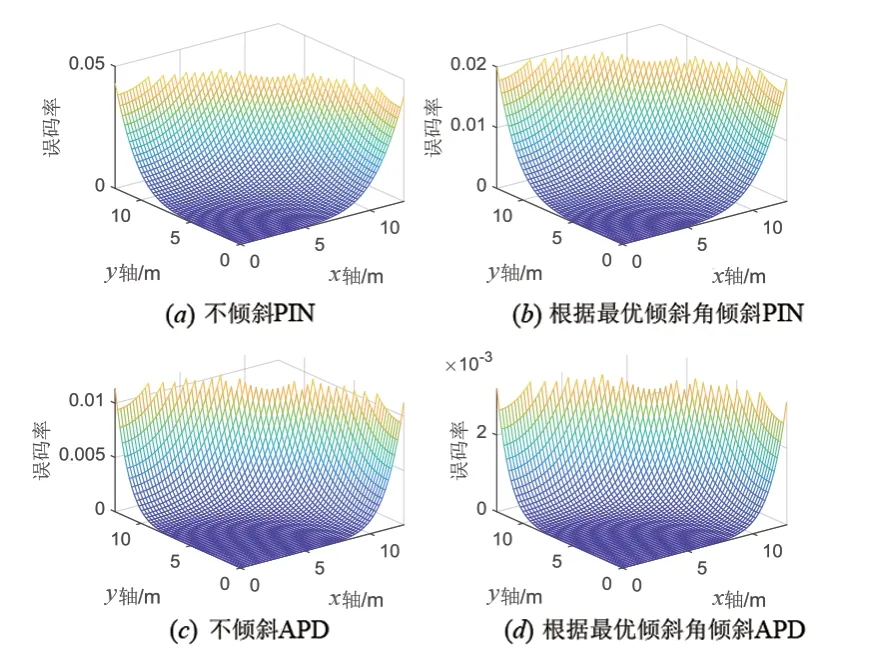
图6 UWOC系统BER随接收机坐标变化曲面

图7 为图1 所示UWOC 系统进行BER 优化后获得的，接收机位于x-y平面不同位置时的最优倾斜角3D曲面分布图. 由前文式（21）和（22）的推导可知，APD 与PIN接收机的BER优化都只和路径损耗L有关，故它们有完全相同的倾斜角优化结果. 从图中仿真结果可以看出：当接收机位于发射光源的正下方时，此时最优倾斜角为0°；而当接收机在平面上移动时，最优倾斜角随接收机距光源距离的增加而逐渐增大；当接收机布置在边界时，最优倾斜角将达到最大值33.2°. 这说明距离光源越远，需要倾斜更大的角度以抵消指向误差cosβ带来的不利影响. 另外，在x-y平面以距光轴z某一固定值为半径作圆的圆周上，最优倾斜角是一致的.

图7 接收机位于x-y平面不同坐标点时最优倾斜角分布曲面图

6 结论

本文主要研究基于APD 和PIN 接收机的，采用强度调制的UWOC 系统BER 性能及其优化. 为此，首先提出了一种含指向误差的DE 路径损耗模型来刻画清澈海洋水质下收发信机处于非对准状况下的信道衰落，并通过MCNS 加以验证. 仿真结果表明，在典型清澈海洋水质有效传输距离之内，由距离导致的纯路径损耗和由指向误差导致的指向损耗可以通过独立乘积方式合成混合路径传输模型，该模型完善了现有UWOC 系统的信道建模. 随后，基于该新信道传输模型，分别推导了APD 和PIN 两种不同PD 接收场景下UWOC 系统的BER 理论表达式，以此对指向误差与BER之间的理论关联进行建模. 理论分析表明，不论采用何种接收PD，BER都是路径损耗的单调递减函数，故而优化系统BER 就可以建模为一个简单的凸优化问题来加以求解. 仿真结果表明，可以根据MCNS 得到的两种不同PD 下的最优部署距离和最佳倾斜角对接收机进行合理布置以及适当倾斜，从而有效改善UWOC 系统的整体误码率性能.