基于样本对元学习的小样本图像分类方法

2022-04-18李维刚李松涛

电子学报 2022年2期

李维刚，甘平，谢璐，李松涛

（武汉科技大学冶金自动化与检测技术教育部工程研究中心，湖北武汉 430081）

1 引言

依靠大数据的监督学习模型极其依赖大量人工标注的标签样本. 在很多领域内，由于缺乏足够的标签样本训练，模型容易过拟合，在测试时分类精度不理想.简单的数据增强和正则化技术并不能使问题得到完全解决［1］. 目前，迁移学习与元学习成为解决这类小样本问题的有效方法，它们都是利用先验知识在小样本任务中快速地掌握新的技能.

迁移学习［2］运用已存在的知识对不同但相关领域问题进行求解. 当目标域标签样本缺乏时，只要源域和目标域相关，迁移学习就能利用从源域中学习的知识帮助目标域模型进行训练，实现已学习知识在相关领域间的复用和迁移.Pan 等［3］将迁移学习方法分为基于样本、基于特征、基于关系以及基于模型四种. 其中，基于特征的迁移是迁移学习领域中最热门的方向，其主要思想是寻找“好”的特征表示来最小化域间差异，但此方法在源域和目标域差异过大时效果不理想.

元学习［4］是解决小样本问题的另一个重要途径，它将学过的知识再利用，让模型快速地学会新任务（Task）［5］. 元学习方法分为基于优化、基于生成式模型、基于记忆单元以及基于度量四种. 在分类问题中，基于度量的元学习方法［1，6］拥有较高的性能表现. 该方法在某一特征空间直接将特征对比度量来执行小样本分类任务，但该类方法对训练集样本数量要求较高，且性能对模型结构敏感度高. 同时，元学习方法通常存在分类精度较低的问题.

对此，本文针对迁移学习、元学习目前困境提出基于样本对元学习（Pairwise-based Meta Learning，PML）的小样本图像分类方法. 其利用传递迁移学习［7］来解决源域与目标域差异过大的问题；同时依据Sun［8］与Chen［9］等的观点，搭建先“迁移学习”，再“元学习”的模型来改善性能；最后，针对元学习特殊的训练范式，提出了元损失函数（Meta Loss，ML），该损失函数利用样本对三种相似性来考虑特征空间中其他样本的影响，以此来扩大正负样本距离，提升PML 模型的性能.

由于钢材的显微组织类型繁多，纹理复杂多变，人工标注极其困难，难以构建大规模训练数据集，因此，仅有Lubbers［10］、DeCost［11］与Azimi［12］等少数人进行了相关研究. 然而，这些方法泛化能力过弱，面对训练类别以外的新型钢材时，性能表现较差. 针对此问题，本文构建了钢材显微组织小样本图像数据集并进行实验来验证PML 模型的有效性，结果表明，PML 方法具有较强的泛化能力，分类精度较佳. 同时，本文将ML损失推广到其它元学习方法中，并在公开数据集mini-ImageNet［13］、tiered-ImageNet［14］上进行实验. 结果表明，ML 能改善元学习方法的性能，验证了ML 损失具有一定通用性.

2 小样本图像分类方法

PML方法如图1所示，包含迁移学习模型与元学习模型两个模块. 迁移学习模型利用传递迁移学习获得特征编码器fθ，将其作为元学习模型的初始特征编码器. 元学习模型采用余弦相似度度量支持集和查询集样本相似度，并利用ML 损失优化fθ参数，提高模型分类精度. 具体阐述如下.

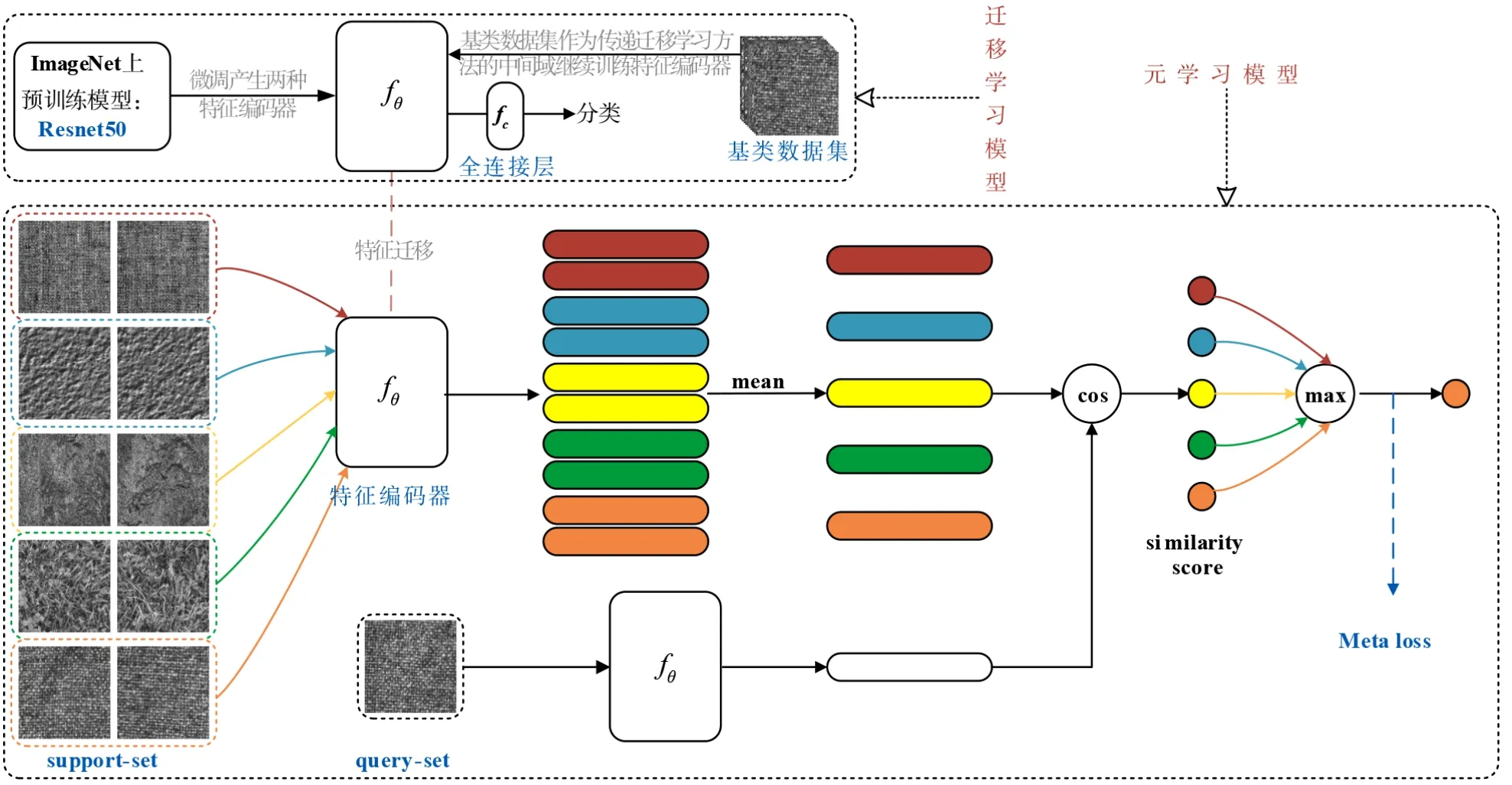
图1 PML方法示意图

2.1 迁移学习模型

构建迁移学习模型是为了获得一个特征编码器fθ，该特征编码器需对新类数据集N（标签样本少）有泛化能力，且不会出现负迁移现象（指在源域上学习到的知识，对目标域上的学习产生负面作用）. 为了获得该特征编码器，本文参考传递迁移学习方法设计该模型，传递迁移学习原理如下所述：

传统迁移学习要求领域间足够相似，而当领域间不相似时，传递迁移学习可利用处于领域间的若干领域，将知识传递式迁移. 其训练范式如图2 所示，通过将源域Ds的特征信息先传递给中间域Di，中间域Di再传递给目标域Dt，帮助预测函数ft(x)更好的执行任务Tt. 其中Ds与Dt具有微弱的相关性，Ds与Di、Dt与Di有一定相关性，且Ds≠Di≠Dt.

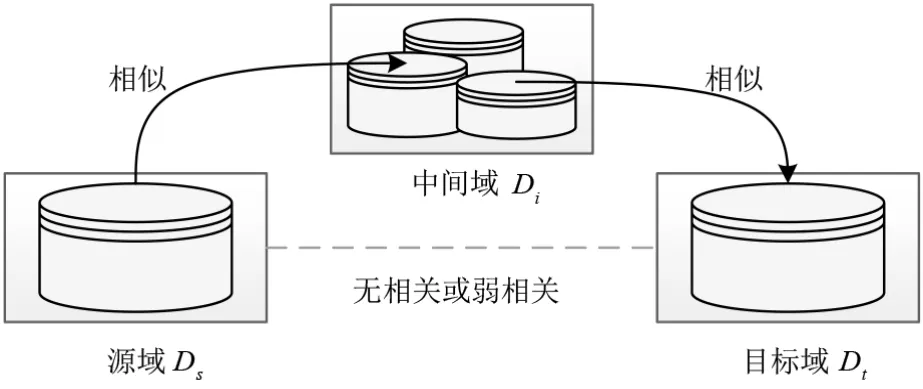
图2 传递迁移学习训练范式

本文使用交叉熵损失在与N 有一定相关性的基类数据集B（中间域）上训练两类初始网络，将删除fc层后得到的fθ作为元学习模型的初始特征编码器. 其中，两类初始网络分别为图3 中path2 路径（Resnet50［15］）与图3 中丢弃stage 5 模块的path1 路径. 第二类初始网络较第一类初始网络参数量更少，输出维度由2048 维降至1024维，训练速度更快，但在某些任务中会损失一定分类精度.

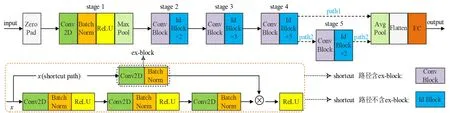
图3 初始网络

2.2 元学习模型

元学习与传统深度学习训练范式不同，其分为元训练（Meta-training）与元测试（Meta-testing）两个阶段.在元训练阶段从基类数据集B 抽取任务（每个任务随机选取不同类别的数据），在这些任务中训练模型. 在元测试阶段，仅提供少量标签样本，即可对新类数据集N进行分类.

具体来说，每个任务随机抽取B中N个类别各K个样本，将其作为支持集. 再从这N个类别剩余数据中抽取M个样本作为查询集. 模型从支持集N×K个样本中学习，以此来识别查询集N×M个样本的类别，这种任务被称为N-wayK-shot任务.

从B 中抽取大量N-wayK-shot 任务. 利用式（1）计算每个任务中支持集第i类样本xi的特征向量均值βi，作为该类质心. 让查询集中样本x分别与N个类质心计算式（2），得出相似度得分pi的集合p，预测样本x为相似度得分最高的类别，并通过最小化损失函数来优化fθ参数. 其中，式（2）中<·，·>表示两个向量的内积，βi也可视为新fc层的预测权重.

元测试即图4 中Meta-testing 过程，其在新类数据集N 上执行与元训练过程相似的步骤. 本文中迁移学习模型利用元测试方法进行评估.

图4 5-way 1-shot元学习范式

3 元损失函数

目前，元学习大多采用交叉熵损失，其只片面考虑查询集中单个样本与支持集样本的关系，并未考虑其它样本对该样本的影响. 对此，本文基于多相似性损失（Multi-Similarity Loss，MS Loss）［16］，提出了能考虑查询集所有样本关系的元损失函数ML. 详细介绍如下.

3.1 多相似性损失函数

将所有样本的特征向量依次设为锚点并与其余样本两两配对，可以构造多个样本对，利用样本对的余弦相似度来度量样本对中两个样本的距离. 余弦相似度越大，即两个样本越相似，特征向量距离越近. 如式（3）所示，余弦相似度即计算样本对中两个样本特征向量xi、xk的内积，式（2）中相似度得分p是余弦相似度在元学习范式中的应用.

目前，大多数度量方法都是利用样本对的自相似性来进行样本对加权，相似性可分为自相似性S、正相对相似性P与负相对相似性N三种.Wang等［16］在Cars-196数据集上进行实验，证明了三种相似性均有正增益，详细实验结果见表1. 其中，自相对性S 对实验结果影响最大.

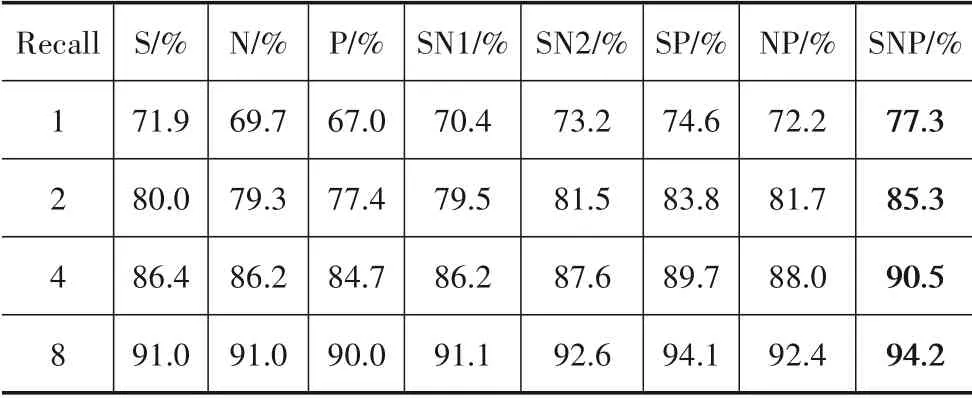
表1 三种相似性在图像检索任务上的性能表现（数据来源于文献[16])

自相似性S 即计算样本对{xi，xk}本身的余弦相似度，它确保在特征空间中正类比负类样本距离锚点更近. 我们把余弦相似度较大的负对（不同类别样本对）和余弦相似度较小的正对（同类样本对）称为困难样本对，其信息量更大，更值得模型去学习. 如图5 中情况1，负对{anchor，neg1}相较于其余负对有更大的余弦相似度，该对即为困难负对.

显然，相似性S 只片面描述了样本对自身的相似性，没有考虑到特征空间中其余样本的影响. 相对相似性结合其他样本与锚点之间的关系解决了这种局限性. 图5 以负样本neg1 为例，结合情况1、2 可知负相对相似性随着其他负对的余弦相似度增加而降低；结合情况2、3 可知正相对相似性随着正对的接近而降低.正样本相对相似性与之类似.

图5 三种样本对相似性示意图

Wang 等［16］将基于样本对的损失函数L 描述成通用对加权（GPW）框架，利用该框架将L 转换为式（4）中计算逐对（pair-wise）相似性的加权：

其中，m为样本总数，Sij为样本对{xi，xj}的余弦相似度，y为样本标签，ωij为样本对{xi，xj}的权重.Wang等人在式（4）的基础上，结合上述样本对三种相似性提出了MS损失. 计算如式（5）所示：

其中，P 和N 分别表示正、负样本集合，α、β为超参数.

公式前半部分控制正样本的紧密程度，对余弦相似度＜λ的正样本进行惩罚；公式后半部分同理.

3.2 基于多相似性的元损失函数

为了更适应元学习训练范式，本文以MS损失为基础提出了元损失函数ML，详见式（6）. 元损失函数是通过图6所示的样本对挖掘和加权两个迭代步骤来实现的. 对比式（5），式（6）中ML只以支持集样本的质心作为锚点，并增加了两个超参数μ(μ≠1)和η(η≠λ），具体说明如下：

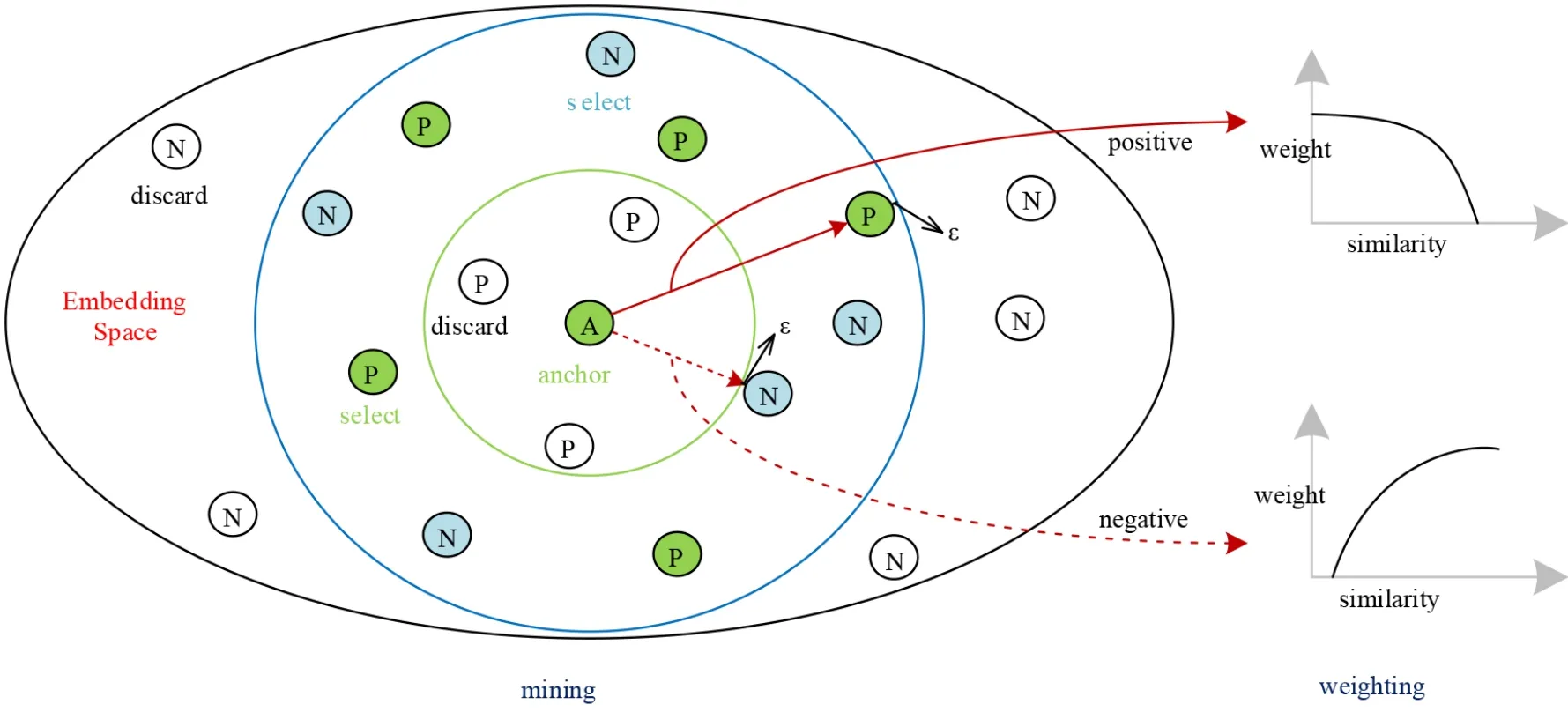
图6 对挖掘和对加权示意图

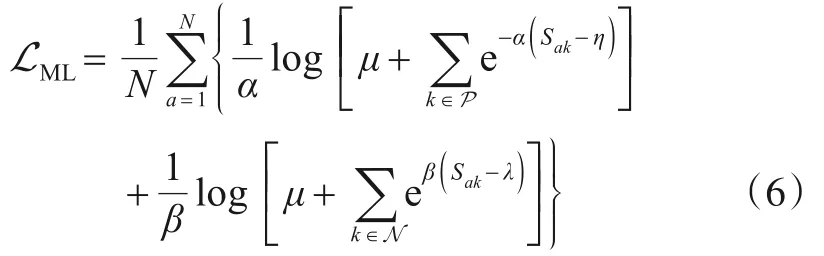
3.2.1 改进的样本对挖掘方案

训练所有样本对耗时过长；而随机采样会被冗余样本对淹没，导致收敛速度慢，模型退化. 对此，MS 损失通过挖掘困难样本对改善了上述问题.

但在元训练任务中，MS 损失是不可行的，这是因为图4 中元学习范式希望查询集样本以支持集样本为基准进行分类；而MS 损失会存在支持集样本以查询集（此时作锚点）样本为基准进行分类.

对此，本文受到LMNN［17］、MS 损失［16］的启发，设计了一种如图6 所示适用于元训练范式的挖掘方案. 具体而言，本文的挖掘方案只将支持集样本设为锚点，锚点与查询集样本两两配对. 然后利用正相对相似性P构造式（7）来挖掘信息量丰富的困难负对，构造式（8）来挖掘信息量丰富的困难正对，同时丢弃其余信息量少的样本对.

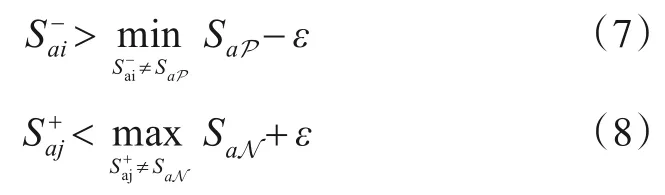
输入：一个任务内所有样本1、利用式（1）求出特征空间中支持集N类样本的质心集合xa；2、xa与特征空间中查询集所有样本两两配对，得到样本对集合R；3、利用式（3）计算集合R中各个样本对的余弦相似度S；4、找出正样本对集合P ∈R中最小余弦相似度样本对{a，P}min；5、找出负样本对集合N ∈R中最大余弦相似度样本对{a，N}max；6、负样本对{xa，xi}的余弦相似度Sai满足式（7）则保留该样本对；7、正样本对{xa，xj}的余弦相似度S+aj满足式（8）则保留该样本对；8、抛弃其余样本对；输出：已保留样本对的集合

3.2.2 改进的样本对加权策略

利用正相对相似性P可以粗略挖掘困难样本对，再结合相似性S 和N，可以进一步对样本对加权. 具体而言，给定负样本对{xa，xi}，i∈N，式（9）为权重ω-ai（式（6）中Sai的偏导数），其对余弦相似度＞λ的负样本进行惩罚；正样本对{xa，xj}，j∈P 的权重ω+aj计算见式（10），其对余弦相似度＜η的正样本进行惩罚. 不同的惩罚阈值可以扩大正负样本差异，更易于区分. 同时，针对最重要的自相似性S，引入μ来改变其在权重中占比. 实验证明，此样本对加权策略在基类B 与新类N 上皆有增益.

图7 中当1、2、3 为负样本时，由式（9）可知负样本对{A，1}权重大小为：Case 1>Case 2>Case 3. 当1、2、3为正样本时，由式（10）可知正样本对｛A，1｝权重ω+aj大小为：Case 3>Case 2>Case 1.

图7 样本对权重示意图

4 实验结果与分析

本文方法基于Pytorch 实现. 图像大小为224×224，采用AdamW［18］优化算法，学习率随代数线性衰减. 迁移学习训练批次为100，迭代200次，初始学习率为1e-6.元学习模型执行5-way 1-shot和5-shot任务（表4例外），查询集大小5×15，训练每代300 个任务，评估每代100个任务，共50 代. 初始学习率为1e-8. 超参数α、β分别为2、50.

4.1 数据集及评价指标介绍

本文从武汉科技大学耐火材料与冶金国家重点实验室获取钢材显微组织图像，构建新类数据集N，将其应用于元测试过程，以此来评估PML 方法.N 由不同放大倍数下的单相和多相显微组织图像组成，共计10 个类别，部分类别示意图如图8所示.

图8 钢材显微组织示意图

同时，本文选取与新类数据集N 相似的公开数据集Kylberg Texture Dataset 作为基类数据集B. 该数据集由28 个类别组成，与N 一样，都是由灰度纹理图像组成，部分类别示意图如图9所示.

图9 Kylberg Texture数据集B部分类别示意图

另外，本文还利用基准数据集mini-ImageNet 与tiered-ImageNet 来评估ML 损失. 评价指标为N个样本平均精度P在95%置信水平下的置信区间（Z=1.96），置信区间半径Rinterval如式（11）所示.

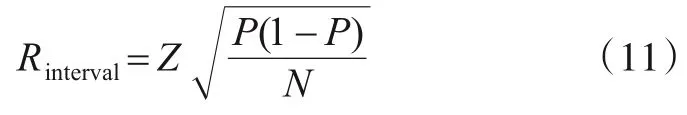
4.2 多相似性损失函数的对比实验

为了验证ML 中样本对挖掘方案与加权策略的重要性，本文在相同实验设置下，针对ML 挖掘与加权方法进行相关研究，其中，超参数ε设置为0.1.

首先使用本文加权策略，将本文与MS 损失的挖掘方案在5-way 1-shot 和5-shot 任务上实验. 如表2 所示，本文挖掘方案优于MS损失挖掘方案. 同时，1-shot与5-shot任务分别使用2 048 维、1 024 维的特征编码器时分类精度更高. 根据Zeiler 等［19］的研究，推测其原因是因为该数据集纹理特征偏多，当执行1-shot 任务时，支持集样本过少，需要高层语义信息的辅助分类；而当执行5-shot 任务时，较多的支持集样本提取的纹理信息足以区分样本，无需高层语义信息. 此外，本文的挖掘方案在1-shot任务上，训练速度分别提升了45%、33%.

接着，本文将式（6）中超参数μ改为1，命为ML-μ损失；将η改为λ，命为ML-η损失. 最后，使用两种特征编码器，以相同的实验设置，在5-way 1-shot 和5-shot 任务中，将交叉熵损失、MS 损失、使用本文挖掘方案的MS损失、ML-μ损失、ML-η损失与ML 损失在N 上进行评估，实验结果见表3.

由表3可知，（1）MS 损失效果不如交叉熵损失；（2）综合②、③可知，本文挖掘方案性能较佳；（3）综合③、④、⑤可知，μ、η（实验优选值）能提升分类精度，证明了改变相似性S 权重占比和以不同阈值对正负样本惩罚皆能提升性能；（4）综合表3可知，ML精度最佳，同时输出2 048 和1 024 维的特征编码器分别适配1-shot 与5-shot任务，这与表2结果相同. 因此，后续实验保持此特征编码器设置.

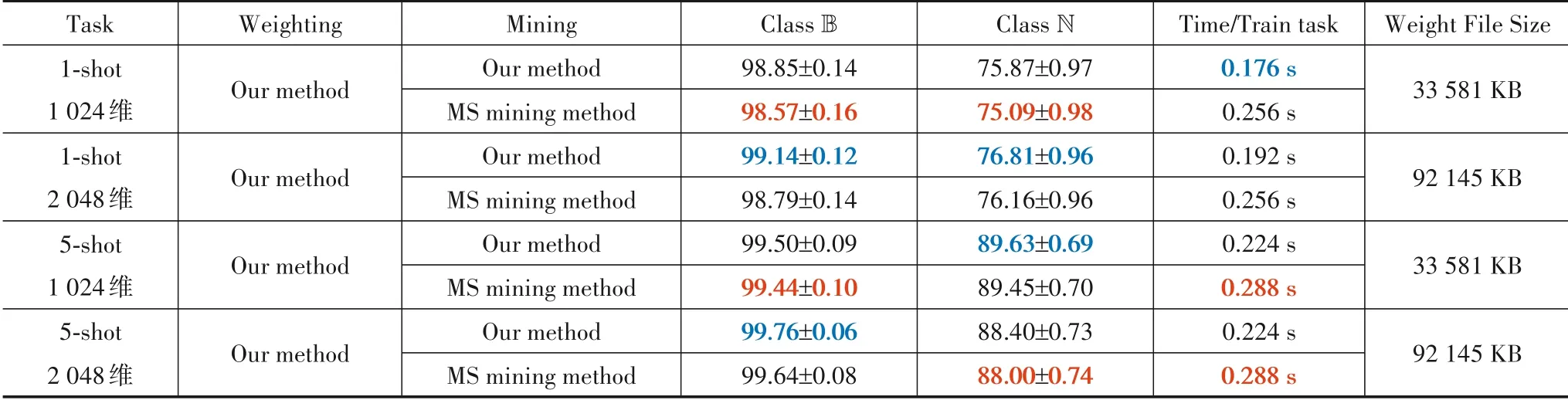
表2 不同挖掘方法下样本平均精度（%）的置信区间及单个训练任务耗时的对比

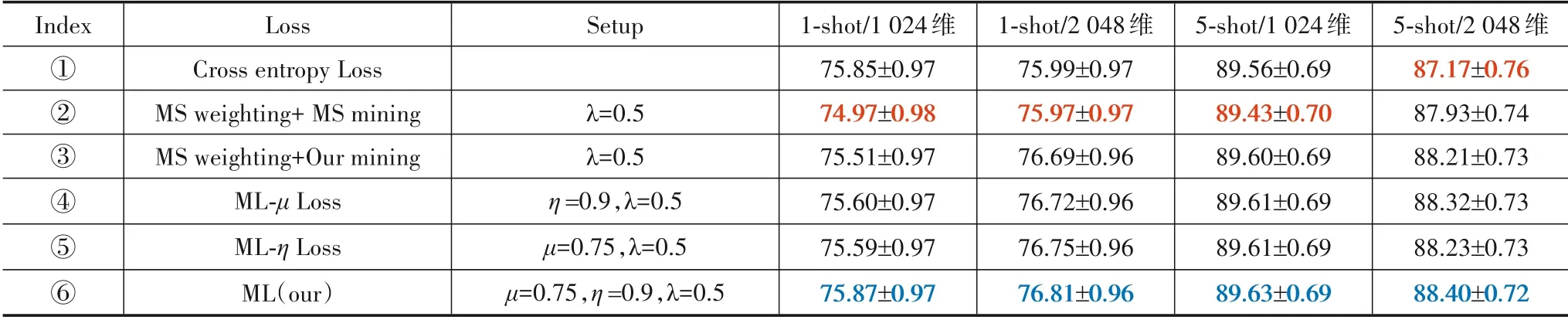
表3 不同损失函数在新类N上样本平均精度（%）的置信区间对比

4.3 迁移学习模型对元学习模型的作用

Sun［8］和Chen［9］等认为迁移学习能提高元学习模型性能. 本文基于此观点将迁移学习获得的特征编码器作为元学习模型的初始特征编码器. 为证实此观点，本文以相同实验设置将图3 中在ImageNet 上预训练的初始网络（Pre-training model）、图1 中元学习模型（Meta model）、未在ImageNet 上预训练的PML 方法（PML-P）、未用基类数据集微调的PML 方法（PML-F）、迁移学习模型（Transfer model）以及本文的PML 方法，按元测试方法在新类N上评估. 结果如图10所示.

图10 不同模型在新类样本上的平均精度（%）

对比图10 中PML-P、PML-F、PML 与Meta model，可以看出Meta model精度最低，证明了迁移学习能优化元学习模型性能；Pre-training model 与Transfer model、PML-F 与PML 两组对比验证了传递迁移学习的有效性. 为了进一步展示PML 较强的泛化性，本文从基类B中抽取大量2-way 5-shot 任务并训练，按元测试方法在新类N 上评估，结果见表4. 综合图10、表4 可知，迁移学习模型一个潜在的重要能力是提高元学习模型的可转移性. PML 方法正是利用此能力来提高模型的泛化性.

表4 不同模型下2类样本平均精度（%）的置信区间

4.4 困难样本对的选取对精度影响的探究

式（7）、（8）中超参数ε约束ML 挖掘困难样本对的范围. 为了探寻ε对精度的影响，本文以相同的实验设置对ε取值进行实验，具体结果见图11，其中ε取0.5 时即挖掘所有样本对，不丢弃任何样本对.

图11 新类数据集N 上不同超参数ε取值下的分类精度

由图11 可知，ML 挖掘的样本对过少时，会丢失部分困难样本对，模型无法充分学习，性能下降；而当ML挖掘的样本对过多时，样本对是高度冗余的，学习冗余样本对会导致模型退化，性能下降.

同时，本文将ML 推广到Chen［9］等提出的Meta-Baseline 模型中，将其损失函数替换为ML，以相同的实验设置，在数据集mini-ImageNet、tiered-ImageNet 上进行实验，结果如图12、13所示.

图12 mini-ImageNet数据集上不同超参数ε取值下的分类精度

图13 tiered-ImageNet数据集上不同超参数ε取值下的分类精度

由图11、12、13可以看出，在ML挖掘的样本对过少或过多时，相较于最佳的样本对挖掘范围，性能均有下降. 进一步论证了上述观点.

4.5 元学习方法精度对比

将PML 方法与其他元学习方法在基类B 上训练后在新类N上评估. 为了公平比较，本文不在元学习阶段应用数据增强. 另外，超参数ε设为4.4节中的最佳值，结果见表5. 可以观察到，PML方法在1-shot任务上精度达到77.65%，高于最新的元学习方法Meta-Baseline 约7.38个百分点；在5-shot任务上精度达到89.65%，错误率为10.35%，相较于Meta-Baseline 的错误率降低了35.31%.

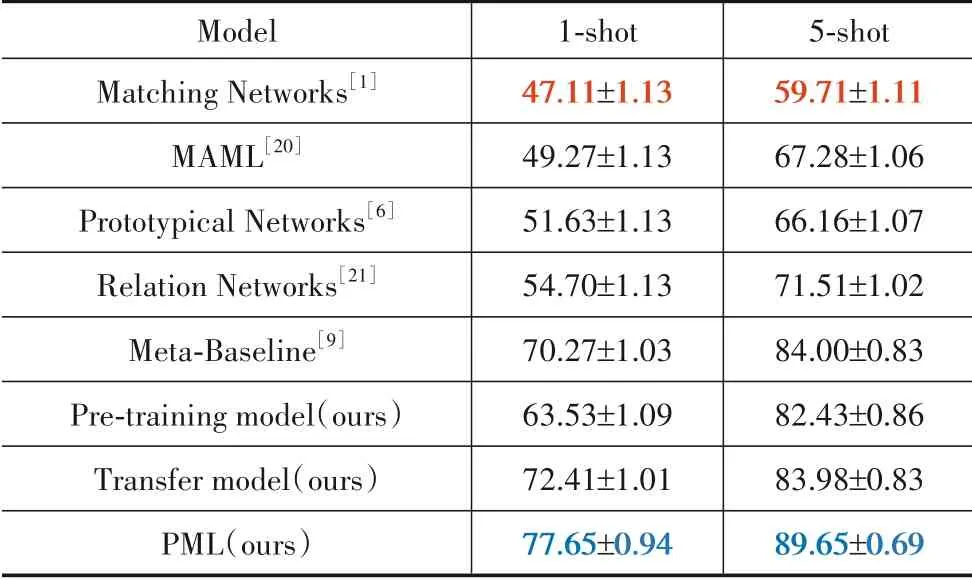
表5 不同元学习对比(在新类上样本平均精度（%）的置信区间)

同时，Pre-training model 与Transfer model 也优于部分元学习方法. 此外，Transfer model 在1-shot 任务上分类精度高于Pre-training model 约8.88 个百分点；在5-shot任务上分类精度高于Pre-training model约1.55个百分点. 综合这些实验结果可知，基于传递迁移学习的Transfer model 方法能利用中间域进一步提升模型在目标域上的泛化能力.

另外，本文以图12、13 中最佳的实验设置将ML 推广到其它元学习方法中，并在mini-ImageNet 和tiered-ImageNet 上与其他元学习方法进行实验比较，实验结果见表6、7.

表6 不同元学习方法在mini-ImageNet数据集上样本平均精度（%）的置信区间(#指应用DropBlock[22]和标签平滑.结果参考文献[9,23,24])

表7 不同元学习方法在tiered-ImageNet数据集上样本平均精度（%）的置信区间(参考文献[9,13]的结果)

由表6、7 可知，在mini-ImageNet 数据集上，Meta-Baseline 模型加ML 损失在1-shot、5-shot 任务上分类精度分别达到64.10%、80.48%，较其他方法拥有更优异的性能表现. 在tiered-ImageNet数据集上也拥有较优的精度. 这表明，本文提出的ML损失能改善元学习性能，具有一定的通用性.