一种基于时空动态图注意力网络的共享出行需求预测方法

骈纬国，吴映波，陈 蒙，蔡俊鹏

（1. 重庆大学汽车协同创新中心，重庆 400044；2. 重庆大学大数据与软件学院，重庆 400044）

1 引言

随着移动互联网和共享经济在全球的迅速发展，共享出行在出行服务中开始扮演越来越重要的角色.滴滴出行、优步、Grab 和长安出行等在线共享出行平台，为人们的出行提供了一种更加便利的方式. 准确的共享出行需求预测可有效协助平台分配车辆、提高车辆利用率、减少用户等待时间、缓解交通堵塞等［1］.

共享出行需求预测是一类基于历史数据的空间和时间特征来预测未来需求的时空数据挖掘任务. 在最新的相关研究工作中，学者们往往使用图卷积网络（Graph Convolutional Network，GCN）来提取城市中的非欧氏空间相关性特征［1～3］. 但传统的GCN 模型在提取空间相关性特征时存在着为不同的邻居节点（区域）分配相同的重要性系数或权重［4］的问题. 此外，现有的基于GCN 的时空预测方法在构建城市结构图时，往往是基于区域地理近邻关系来建立图中节点（区域）之间边的关系. 这种方式所构建的城市结构图是一种在不同的时间间隔中保持一致的非时间特定性的静态空间图结构，不利于针对不同的时间间隔来动态地提取空间相关性特征.

针对上述问题，本文提出一种基于时空动态图注意力网络（Spatial-Temporal Dynamic Graph Attention Networks，STDGAT）的共享出行需求预测方法. 在STDGAT 中，图注意力网络（Graph Attention Network，GAT）［4］被用来提取区域间的非欧氏空间相关性特征.基于注意力机制［5］，GAT可为城市结构图中节点的不同的邻居节点自适应分配不同的重要性系数，以实现对不同邻居区域的自适应重要性分配. 此外，该方法使用基于通勤关系的时间特定性动态空间图结构，以建立在不同时间间隔具有时间特定性的动态空间关联性.具体而言，如图1 所示，若在时间间隔t中存在从区域A到区域B的用车通勤，但不存在从区域B到区域A的用车通勤，则在时间间隔t中的城市空间图中存在从节点A到节点B的有向边，但不存在从节点B到节点A的有向边，即对于节点A来说，节点B是其邻居节点，但对于节点B来说，节点A不是其邻居节点. 如果在时间间隔t中，区域A和区域B之间不存在用车通勤（双向均不存在），则在时间间隔t中节点A和节点B之间不存在任何边连接关系，即节点A和节点B互相不为邻居节点. 通过这种方式，城市空间图可由静态的图结构变为具有时间特定性的动态图结构，以此来建立具有时间特定性的动态空间关联性.

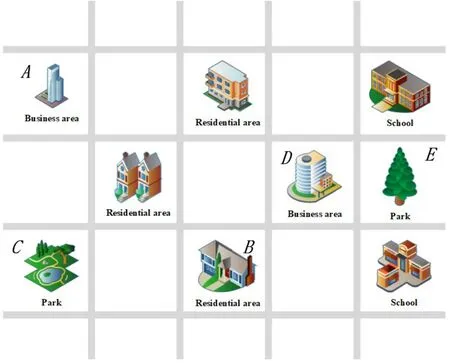
图1 城市的不同区域

通过在一个大规模的共享出行数据集上对本文提出的基于STDGAT 的共享出行需求预测方法进行实验验证. 实验结果表明，该方法在RMSE，MAPE 和MAE 3个评价指标上均优于相关基准比较方法.

2 相关工作

传统的时空预测方法主要依赖时间序列中的统计信息来回归得到最终的预测结果. 自回归移动平均模型（Autoregressive Integrated Moving Average，ARIMA）是其中的一个代表性方法，并在一些传统的交通预测任务中得到了广泛的应用［6，7］. 胡文斌等人［8］提出了用于城市交通导航的多路口导航量搜索方法. 为了提高模型的预测准确率，一些额外的信息也被研究人员加入模型中来辅助模型的预测，例如天气状况和节假日信息等［9～12］.

近年来，研究人员开始广泛应用深度学习方法来解决相关问题.Zhang 等人［9］提出了一个基于深度卷积神经网络的方法来预测城市人流量，在此之后，他们进一步将残差连接［13］加入他们的模型中，并提出了用于城市人流量预测的ST-ResNet［10］. Wang 等人［14］提出了用于出租车供需预测的多层全连接神经网络. Yu 等人［15］和Zhao 等人［16］分别提出了基于长短期记忆（Long Short-Term Memory，LSTM）和双向长短期记忆（Bi-directional Long Short-Term Memory，BiLSTM）的时空预测方法. Yao 等人［17］使用卷积神经网络（Convolutional Neural Network，CNN）和循环神经网络（Recurrent Neural Network，RNN）来提取联合时空特征，并在此基础上使用了图嵌入（Graph Embedding）方法来获取远距离区域之间的语义相关性特征.Qiu等人［18］提出了一个用于出租车起始点-终点需求预测的情景化时空网络.

为了捕获不规则的非欧几里得空间相关性，Li 等人［3］提出了用于交通预测的基于扩散卷积的循环神经网络；Yu 等人［2］提出了基于GCN 的STGCN 模型；在这之后，Geng 等人［1］构建了基于邻居关系、功能相似性和交通连通性的多图结构模型，以此来捕获更加多样性的非欧氏空间相关性.

3 基于时空动态图注意力网络的共享出行需求预测方法

3.1 共享出行需求预测问题定义

共享出行需求预测任务是一种基于历史时空数据的时间序列预测任务，具体而言，是根据过去多个连续时间间隔中的需求序列数据来预测未来一个时间间隔中全局需求量的任务. 其中给定的历史需求序列是从时间间隔t-L+ 1到当前时间间隔t.

本文首先根据真实的地理坐标（经度和纬度）对整个城市进行分割，因此每个区域的真实形状是规则的矩形，并被抽象成一个点来进行建模. 因此，预测任务可以表示为

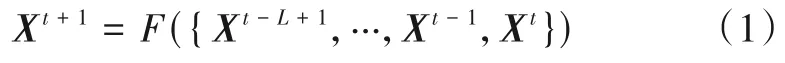
其中，Xt表示在t时刻所有区域的需求量的集合，F(·)表示预测模型.

3.2 模型整体结构

图2 展示了STDGAT 的整体框架结构.STDGAT 由空间模块、时间模块和输出预测层3个部分组成.

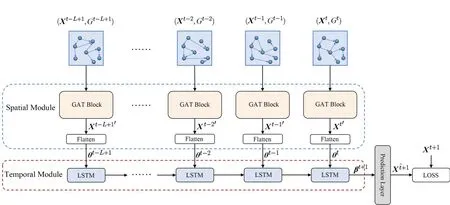
图2 模型整体框架结构

3.2.1 空间模块

空间模块（Spatial Module）用于在每个时间间隔中，提取全局的空间特征. 空间模块包含一个由多个图注意力层（Graph Attention Layer，GAT）层组成的GAT Block. 其内部结构如图3所示.

图3 GAT Block内部结构

GAT 层通过学习节点间的注意力因子来更新每个节点的隐藏特征. 通过使用GAT 层来提取空间相关性特征，模型为城市结构图中节点的不同邻居节点分配了不同的重要性系数，从而实现了自适应的空间相关性特征提取. 具体的操作过程如下所述.

被GAT 层操作的图被定义为G =（V，E），其中，V和E分别表示图G中的节点和边的集合. 在节点集合V中vi表示节点集合V中的第i个节点. 基于上述定义，节点vi在第l层的特征向量表示为hi∈Rd(l)，其中，d(l)表示节点vi在第l层的特征向量的长度. 为了在不同的时间间隔中提取具有时间特定性的动态空间相关性特征，STDGAT 基于区域间通勤关系构建了具有时间特定性的动态空间图结构，并在空间模块中使用GAT 层来自适应地提取具有时间特定性的动态空间关联性特征. 因此，上述概念被进一步定义为，Gt= (V，Et)和∈Rd(l)，分别表示在时间间隔t中的节点、图和特征向量.

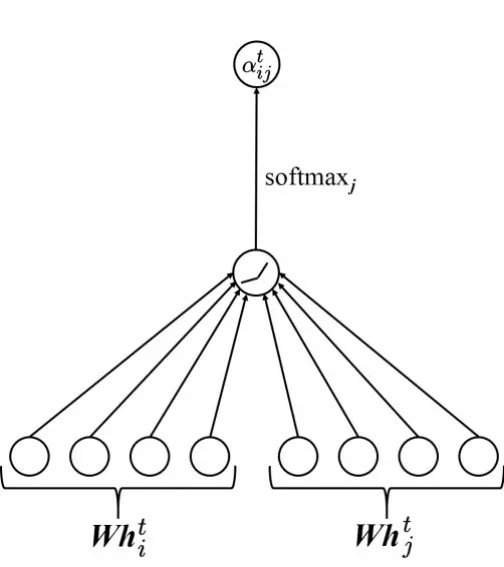
图4 图注意力层

其中，W∈Rd(l+1)×d(l)是第l层的可训练参数，a(·，·)是用于计算节点和节点之间关联性的函数. 需要注意的是，，其中表示节点在时间间隔t中的邻居节点的集合. 关于函数a(·，·)的选择，学者们通常使用一个可训练的前馈神经网络［4］. 因此，在t时刻，节点vti与其邻居节点之间的注意力因子可以被表示为

其中，(·)T和||分别表示矩阵的转置操作和拼接操作. 在进行完上述操作之后，softmax 函数被用来对注意力因子进行归一化操作.

最后，通过使用上述归一化注意力因子来加权求和得到节点vti新的特征向量，具体过程为

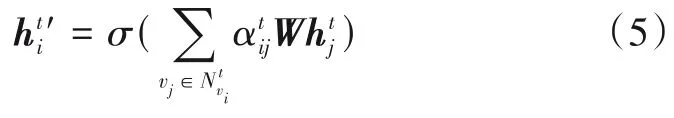
在GAT Block中，每个GAT层的操作被表示为

其中，Xt l∈RN×d(l)表示在时间间隔t中第l个GAT 层的输入，fl(·)表示第l个图注意力层的操作，N和d(l)分别表示城市的区域总数和第l层中每个节点的特征向量长度. 因此，时间间隔t中的需求Xt在经过GAT Block之后变为

其中，Xt′ ∈RN×d表示在时间间隔t中从GAT Block输出的空间特征，d表示在经过了GAT Block 之后每个节点的特征向量长度. 在经过了图注意力操作之后，在时间间隔t中从GAT Block 输出的特征矩阵Xt′被展开为一个特征向量θt∈RNd. 最后，长度为L的需求序列经过空间模块后，输出的空间特征序列St+1∈RL×Nd表示为

3.2.2 时间模块

在时间依赖性建模中，循环神经网络（Recurrent Neural Networks，RNN）已被证明可以取得良好的效果［19］，长短期记忆（LSTM）的引入克服了传统的RNN 难以学习长期依赖性关系的缺点［20］. 此外，已有的关于时空预测的文献表明，LSTM 在处理这种时序数据时具有优异的表现［1，17，18］. 因此，本文在STDGAT 的时间模块（Temporal Module）中，使用了LSTM 来对需求序列的时间依赖性进行建模.

LSTM 引入了一个记忆单元ct来累积序列中之前时刻的信息. 具体而言，在t时刻，给定输入xt，LSTM 使用一个输入门it和一个遗忘门ft来更新记忆单元ct，并且使用一个输出门ot来控制隐藏状态ht. 其表达式为

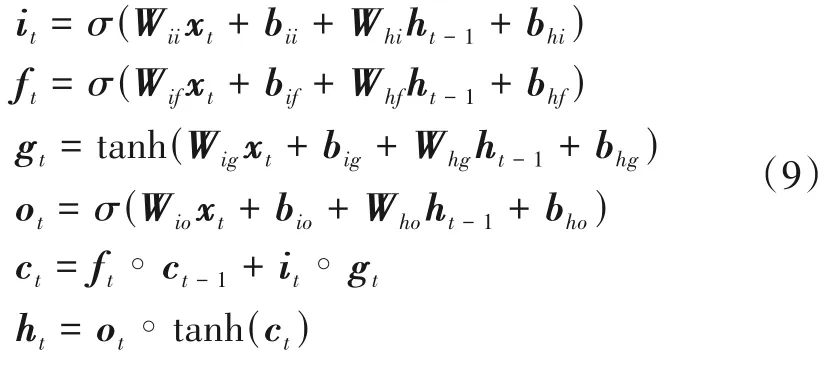
其中，∘表示Hadamard 乘积，σ表示sigmoid 激活函数，Wpq和bpq(p∈(i，h)，q∈(i，f，g，o))为LSTM 的可训练参数，ct和ht分别表示在t时刻记忆单元状态和隐藏状态.关于更多LSTM的细节，请参考文献［20～22］.

如图2 所示，LSTM 将空间模块输出的空间特征序列St+1作为输入，然后输出时空联合特征向量βt+ 1∈Rk.

3.2.3 输出预测层

输出预测层（Prediction Layer）旨在将联合特征向量βt+1映射为需求向量，以此作为最终的预测结果. 本文使用了一个具有N个神经元的全连接层作为最后的输出预测层（N代表城市中的区域总数）. 输出预测层的公式可表示为

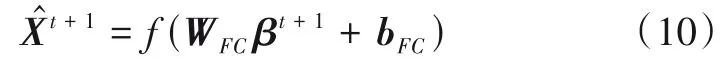
其中，+1表示最终的预测结果，WFC和bFC分别表示输出预测层的权重和偏置，f(·)为激活函数.

4 实验与分析

4.1 实验数据集与参数设置

本文实验使用来自滴滴出行的共享出行数据集（https：//gaia.didichuxing.com）. 该数据集包含海口市从2017 年5 月1 日到2017 年10 月31 日的共享出行订单数据，数据集包含有121 个区域，每个区域的大小约为1 km × 1 km. 在本文实验中，时间间隔设置为1 h，数据集中的总订单数为12 185 427，总时间间隔数为4 416.

并将2017 年5 月1 日至2017 年9 月30 日的数据作为训练集，剩余数据（2017年10月1日至2017年10月31日）作为测试集. 在训练集中，80%的数据用来训练模型，剩余20%用作验证集.

在STDGAT中，输入序列长度L被设置为5. 在空间模块中，GAT Block 包含3 个GAT 层，每一层均包含32个隐藏单元. 在时间模块中，LSTM 的隐藏层数量为1，并包含512个神经元.GAT层中的激活函数为LeakyRe-LU，在输出预测层中的激活函数为ReLU. 本文通过Adam［23］优化器来对网络进行优化. 在训练过程中，学习率和权重衰减值分别为1e-3 和5e-5. 模型的代码基于深度学习库Pytorch［24］编写，并在两块NVIDIA 1080Ti GPU上进行训练，最大训练轮数为200.

4.2 损失函数

在训练阶段，STDGAT 使用均方误差（Mean Square Error，MSE）作为损失函数，并通过使其最小化的方式来训练模型.MSE的公式可表示为

其中，Θ 表示模型的所有可训练参数，yi和分别表示真实值和预测值，z表示训练样本的总数.

4.3 评价指标

本文采用了3 种适用于共享出行需求预测任务的评价指标，分别为均方根误差（Rooted Mean Square Error，RMSE），平均百分比误差（Mean Average Percentage Error，MAPE）和平均绝对误差（Mean Absolute Error，MAE），计算式为

其中，yi和分别表示真实值和预测值，z表示测试样本的总数.

4.4 与基准模型的对比

将STDGAT 分别与历史平均（Historical Average，HA）、自回归移动平均（Autoregressive Integrated Moving Average，ARIMA）、Lasso 回归（Lasso regression，Lasso）、岭回归（Ridge regression，Ridge）、XGBoost［25］、多层感知机（Multiple Layer Perception，MLP）、DMVST-Net［17］、DCRNN［3］、STGCN［2］、ST-MGCN［1］基准预测方法进行实验对比分析. 表1展示了基准模型和STDGAT的实验结果. 从表中可以看出，STDGAT 在3 个评价指标上均达到了最佳效果.HA 和ARIMA 的预测误差最大，这是由于这2个模型只能依靠历史真实的数据值来进行预测，并没有考虑任何相关特征的提取. 由于考虑了序列中更多的上下文信息，线性回归模型（Lasso和Ridge）的表现要优于HA 和ARIMA. 但是，线性回归模型同样无法提取更多的特征来进行预测，因此线性回归方法的预测误差依然较大. XGBoost 和MLP 进一步对输入序列进行了变换，并提取了序列中的隐藏特征，因此，它们的表现相比于上述4 种方法，得到了进一步的提升. 但是，XGBoost和MLP依然没能在空间维度或时间维度上对数据进行建模.

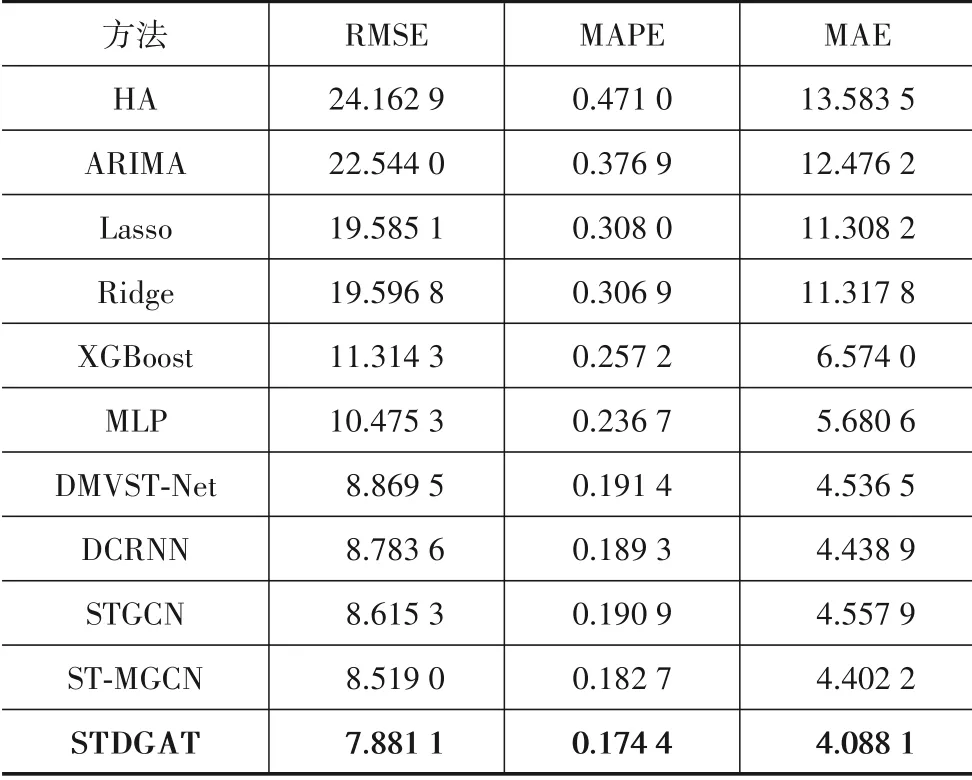
表1 与基准模型的对比

4 个深度学习方法（DMVST-Net，DCRNN，STGCN，ST-MGCN）进一步考虑了时空依赖，因此它们达到了较为理想的效果. 与这3 种方法相比，由于考虑了不同邻居区域间的自适应空间相关性和具有时间特定性的动态空间图结构，STDGAT 的表现更加优异. 具体而言，DMVST-Net 在提取全局空间特征时，仅仅将一个固定的静态图嵌入到一个向量中，这种方式对于提取自适应和动态空间相关性具有局限性. DCRNN，STGCN 和ST-MGCN 对区域间的非欧氏空间相关性进行了建模.但是，由于这两种方法在对非欧氏空间相关性进行建模时，使用的是传统的GCN 模型，因此这两种方法只能使每个区域为其不同的邻居区域分配相同的重要性系数. 此外，DCRNN，STGCN 与ST-MGCN 并没有考虑具有时间特定性的动态空间图结构，因此，它们的效果相比于STDGAT要略显逊色.

4.5 在不同时间的实验结果

为探讨在不同时间段上预测效果的差异，本文分别在不同时间段中进行了实验.

图5 展示了在一周7 天中，STDGAT 和所有基准模型的表现. 图6展示了在一周7天中，STDGAT 与4个深度学习基准模型的表现. 如图中所示，STDGAT 在各个时间段上都取得了最佳的表现，这证明了STDGAT具有很好的鲁棒性. 表2展示了STDGAT和基准模型分别在工作日和周末的实验结果. 如表中所示，STDGAT 无论是在工作日还是周末都具有最佳的效果.

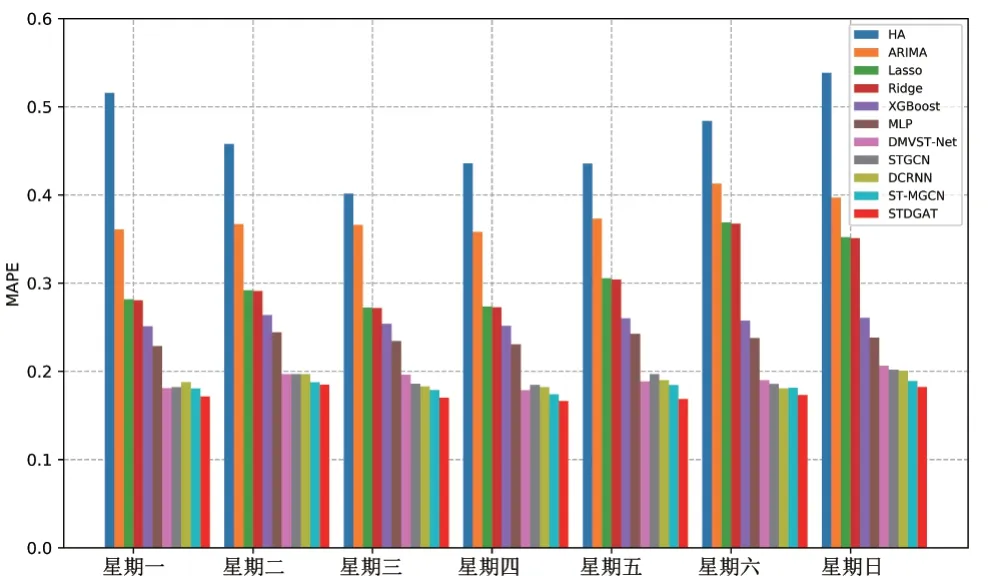
图5 模型在不同天的表现

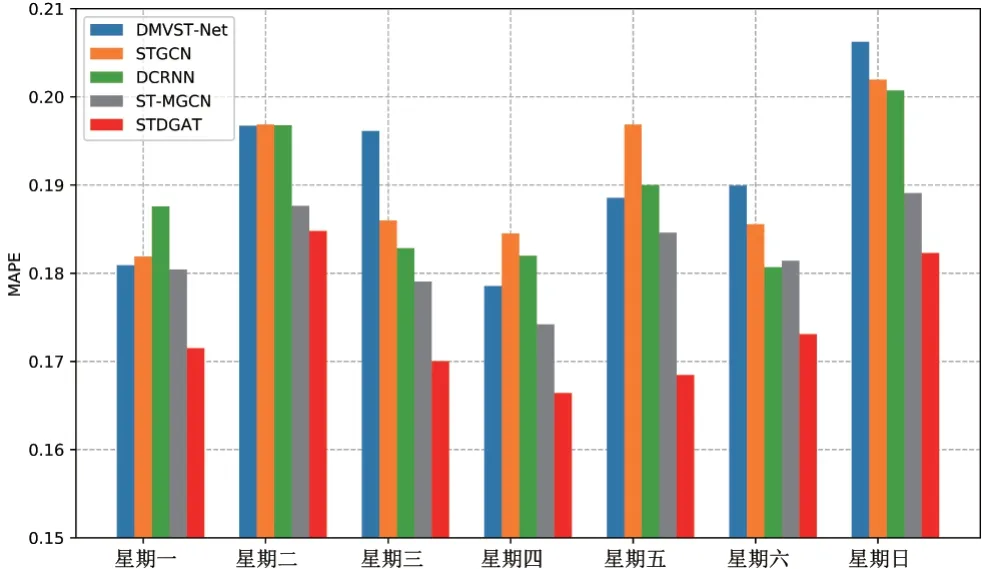
图6 深度学习模型在不同天的表现

但实验结果中所有方法在工作日的表现均优于在周末的表现. 其中的原因在Yao 等人［17］的工作中得到了相关解释，即相比于工作日的需求模式，周末的需求模式要更加不规则. 由于规则的需求模式更加有利于模型去学习，因此在工作日中，模型的表现要更加优于在周末的表现.

4.6 STDGAT的变体模型

STDGAT 有2 个不同的特征提取模块：空间模块和时间模块. 为了探索这2 个模块对预测结果的影响，本文构建如下变体模型.（1）Spatial module + Prediction layer. 该网络由STDGAT 的空间模块和输出预测层组成. 该网络仅提取空间特征来进行预测，以此来探讨在缺乏时间特征提取时模型的性能.（2）Temporal module+ Prediction layer. 该网络由STDGAT 的时间模块和输出预测层组成. 该网络仅提取时间特征来进行预测，以此来探讨在缺乏空间特征提取时模型的性能.

表3展示了上述变体模型与完整版STDGAT的实验结果对比. 在缺少了空间模块或时间模块时，STDGAT的效果会得到大幅度下降. 由此可见，空间模块和时间模块在STDGAT中均具有重要的作用，两者缺一不可.

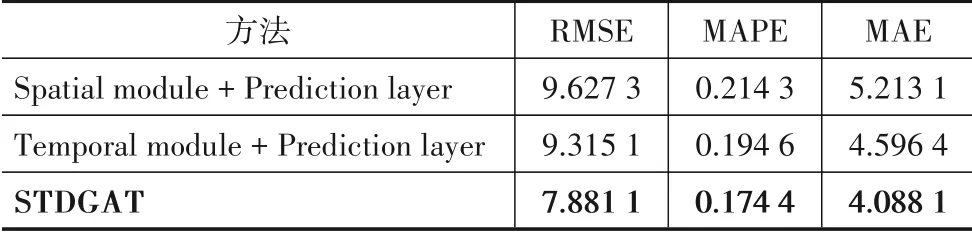
表3 不同模块的表现对比

实验也表明了STDGAT 在共享出行需求预测任务中达到了优异的效果，也验证了不同特征提取模块的合理性和有效性.

针对基于通勤关系的时间特定性空间图结构，本文构建了STDGAT-fixed 变体模型进行实验对比，以此来验证其有效性.

STDGAT-fixed是STDGAT的变体，在提取空间特征时，该模型使用了一种在不同时间间隔中保持固定的静态空间图结构，这种图结构是基于真实的区域地理邻接关系构建的，以此来代替STDGAT中基于通勤关系的时间特定性空间图结构.

STDGAT-fixed 与STDGAT 的实验结果对比如表4所示. 其中，STDGAT 的3 个评价指标上的表现均优于STDGAT-fixed，这意味着本文所提出的基于通勤关系的时间特定性空间图结构在共享出行需求预测任务中，具有比传统的基于区域真实地理邻接关系的图结构更加优异的表现. 这也证明了在图学习中，相比于静态的空间图结构，动态空间图结构是一种更加可行有效的图表示学习方式.

表4 STDGAT与变体模型STDGAT-fixed的对比

4.7 序列长度与GAT层数对实验结果的影响

实验分别探讨了输入到模型中的序列长度与GAT层数对预测结果的影响.

图7 展示了输入序列长度对预测结果的影响. 如图中所示，当输入序列长度为5时，模型达到最佳性能.当输入序列长度小于5时，预测误差随着序列长度的增加而减小，这表示随着序列长度的增加，模型可以学习到更长的时间依赖性信息，这些信息有助于对结果的预测. 但是当输入序列长度大于5 时，模型的效果会有略微下降，并伴随着一些波动. 造成这种现象的一个潜在原因是，随着输入序列长度的增加，输入到模型中的信息量呈线性增长，因此模型需要将更多的信息与梯度计算过程联系起来，并会造成一定程度上的信息丢失，因此训练过程会变得更加困难.

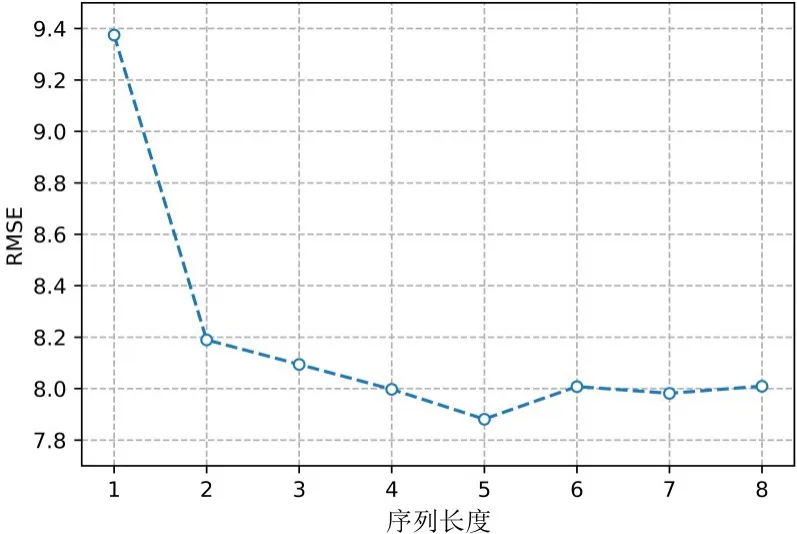
图7 不同输入序列长度的实验结果（RMSE）

图8 展示了空间模块中GAT Block 中的GAT 层数对实验结果的影响. 从图中可以看出，随着GAT 层数由0 增加到5，RMSE 值逐渐降低. 这意味着，随着GAT层数的增加，模型的效果变得更好. 造成这种现象的原因可解释为，随着层数的加深，原始的特征将进一步和其邻居中的特征进行聚合，这将使较深的层具有更大的感受野. 由于更大的感受野可以捕获更多的空间关联性，因此，随着层数的加深，模型可以学习更多的空间信息来提高其性能.

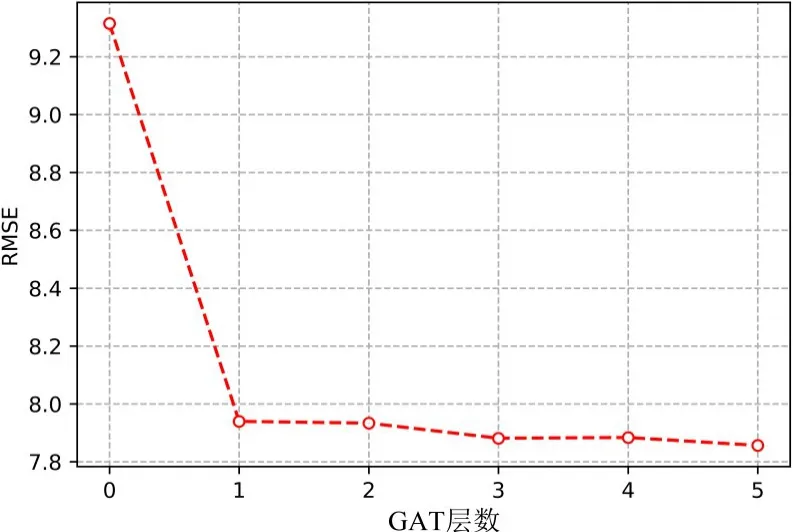
图8 不同GAT层数的实验结果（RMSE）

5 结论

本文提出了一种用于共享出行需求预测的时空动态图注意力网络. 针对共享出行需求预测在空间特征提取时存在的非自适应邻居区域重要性分配和静态空间相关性建模的问题，本文基于图注意力网络和时间特定性动态空间图结构有效地解决了这2个问题，并通过大量的实验验证了模型的有效性和合理性，为未来的相关研究工作提供了参考.