河道开挖卸荷对堤岸变形破坏影响分析
2022-04-18王琦
王 琦
(辽阳市防汛抗旱河务服务中心,辽宁 辽阳 111000)
1 概述
在天然河流中经常发生冲刷和淤积现象,容易发生水害,妨碍水利发展。为适应除患兴利要求,必须采取适当措施对河道进行整治,包括治导、疏浚和护岸等工程[1]。然而,一河岸工程在施工过程中由于未开展有效的稳定性评价,尤其是河道土方开挖工程,造成堤岸存在或出现明显的破坏变形趋势,为河堤工程的后期安全运行埋下隐患,同时也造成一定经济损失[2]。因此分析河道开挖工程中岸坡的稳定性是河道洪水期与枯水期安全运行的关键问题[3]。
目前,国内外通常采用数值模拟的方法来分析河道工程在施工过程中的变形破坏,其常用的数值理论包括有限元法、有限差分法、离散元法[4-10]等。文中所采用的ABAQUS软件有着成熟的理论基础,当中包含多种类型的材料模型库,可以模拟土壤与岩石等地质材料的应力应变以及位移变形分析,同时还能对材料损伤破坏进行二次开发模拟,因此被广泛用于土方开挖工程[11]。
以某河道土方开挖工程为例,采用ABAQUS建立了2维河道开挖模型,在有限元方法基础上采用强度折减法,采用M-C模型分析了河道卸荷过程坡体的塑性应变、位移以及安全系数,并根据数值结果提出了相关加固措施。研究结果可为相关工程分析提供参考。
2 模型建立与计算参数
本次河道土方开挖长度5.3 km,地貌为河谷平原地区,现根据工程设计,在开挖时按两次不同坡比进行放坡,第一台阶坡比按照1∶1.5的比例进行放坡,留平台6.7 m宽,第二次开挖则按照1∶2的坡比进行放坡,开挖后左右两岸坡底距离为20 m。此次土方开挖深度15.24 m,在第一次放坡后,分别按照单次1.28 m的深度逐步开挖,一共开挖8步。经现场勘查,整个地基材料可分为4层,从上往下依次为灰黏土、黏土1、黏土2、粉质黏土。此外,计算模型简化为平面应变模型,采用M-C屈服理论,土的最大主应力取1 kPa,损伤位移取0.02 mm。图1为本次概化模型尺寸,表1为本次计算力学参数。
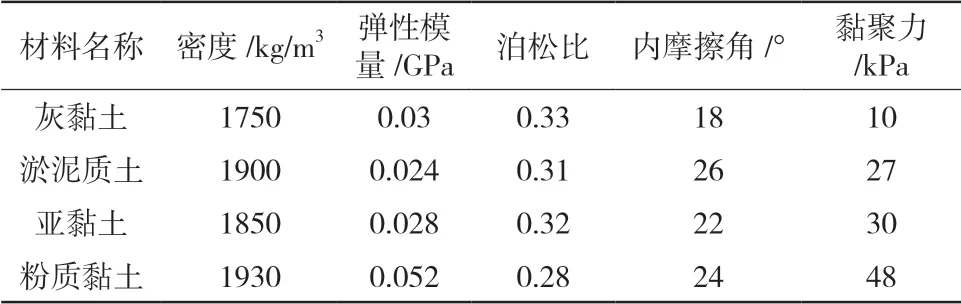
表1 模型计算力学参数
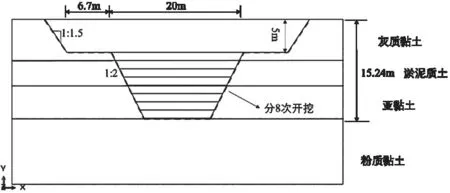
图1 河道开挖横河断面
3 数值结果分析
3.1 卸荷过程坡体变形分析
图2为不同开挖步数下,模型的塑性应变云图。如图2所示,在第一次卸荷后,河道底部的塑性应变最大且范围最广,这是由于河道底端土体的自重应力最大,而应力历史对土体力学性质有着至关重要的作用,固结压力最大,应力路径的影响程度就越大,因此,埋深越深,卸荷后河道底部的变形就越明显。此外还可看到,在第一次卸荷后,淤泥质土和亚黏土两端的接触面也产生了一定范围的塑性应变,但此时第一次放坡形成的堤岸并未发生明显的塑性变形。第一次放坡结束后,继续按照第二次放坡的工程设计进行开挖,即图2中的step2,此时与第一次放坡相比,卸荷后只存在河道粉黏土地基两端的塑性应变有小范围的扩大。而当开挖到step3时,第一次放坡形成的边坡坡角附近开始出现塑性变形区域,而土体其余部分维持着与之前相似的变形范围,一直持续到step6。而当工程开挖到step7时,第二次开挖所形成的边坡坡角开始出现塑性破坏,且破坏范围随着开挖的深度而逐渐扩大。当开挖到设计高度后,其坡角的塑变破坏范围约为临空面长度的1/3。从整个开挖过程来看,卸荷对岸坡的影响存在临界值。为防治边坡的滑动变形,当卸荷深度为7.6 m时,应当对第一次放坡形成的边坡进行抗滑桩或土钉加固,而当卸荷深度为11.4 m时候,应当对第二次放坡所形成的边坡采取加固措施。
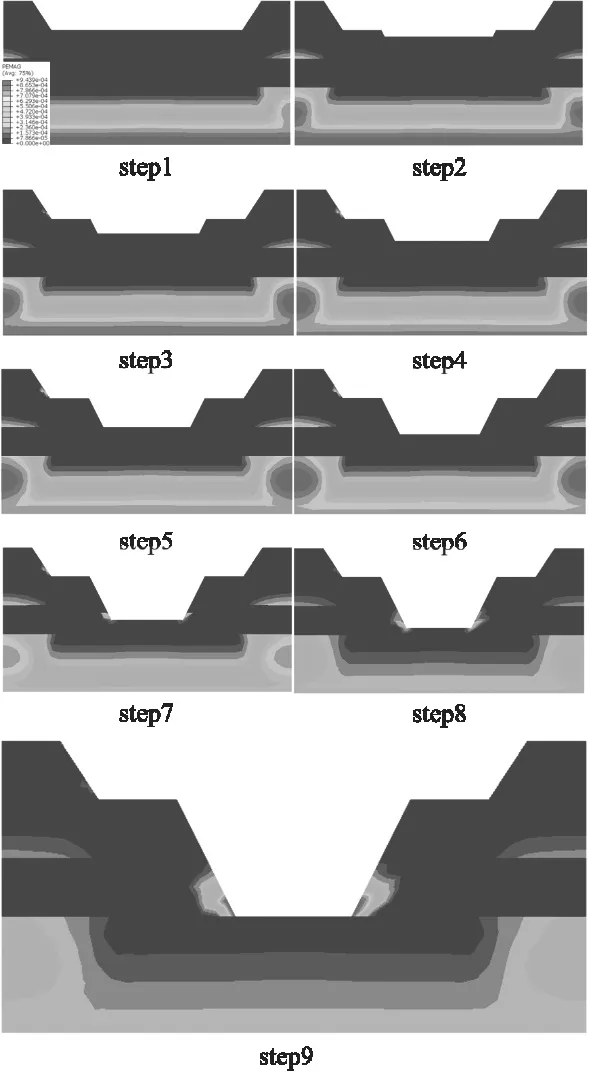
图2 不同开挖步数下模型的塑性应变云图
3.2 卸荷过程中坡体位移分析
为分析河道在卸荷过程中,河道水平位移的变化情况,将不同开挖步数下的河道位移云图进行输出,如图3所示。在第一次放坡结束后,在河道的亚黏土层产生了较大的向右的水平位移,而此时堤顶部分范围产生了负位移,说明岸坡有向右滑动趋势。当第二次放坡,继续开挖至位移变形较大处时(step5),此时第二次开挖所形成的边坡坡角具有较大的水平位移,但随着开挖深度的逐渐增加,河道左岸正水平位移的数值较大的范围逐渐减少。
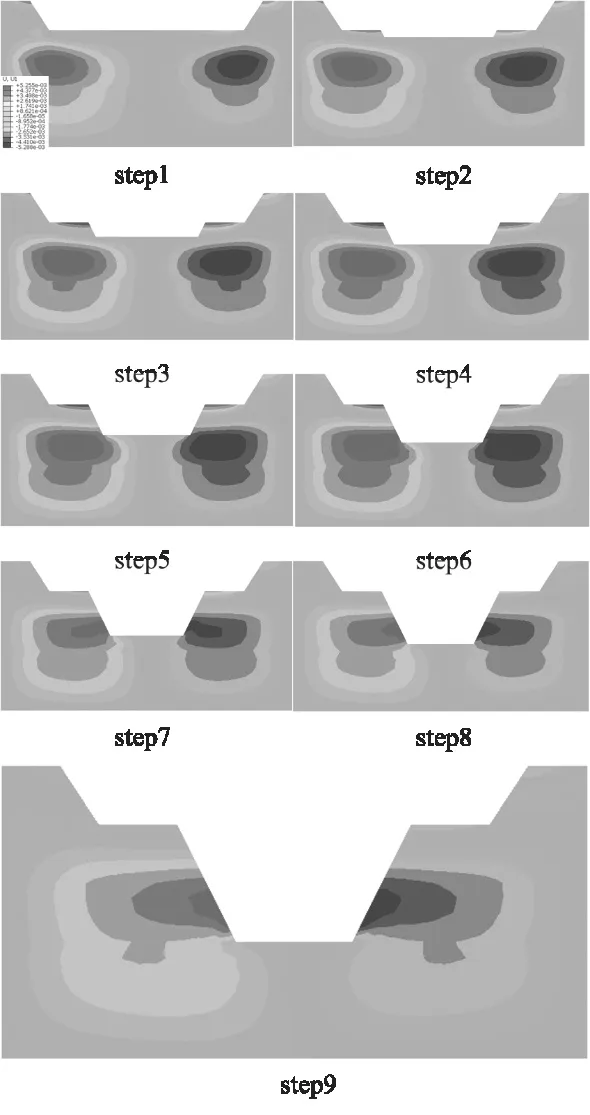
图3 不同开挖步数下的河道位移云图
从图3可明显看到,开挖结束后,河道迎水面的水平位移最大,为进一步分析定量分析迎水面的水平位移变化趋势,考虑到左右岸的对称性,将左岸迎水面坡顶至坡角的节点位移输出,如图4所示,坡顶产生了负的水平位移,有向左滑动趋势,约为4.5 mm,但随着与坡顶点相对距离的增大,坡面开始逐渐向右移动,当相对距离为8.4 m时,水平位移达到最大,达到了14.7 mm,之后又逐渐减小。因此从迎水面的水平位移变化趋势可知,在距离二级边坡顶点的8.4 m处,应为岸坡潜在滑动面剪出口,因此,在开挖到这一步之前,应当采取适当的支挡结构进行加固,防治滑动。
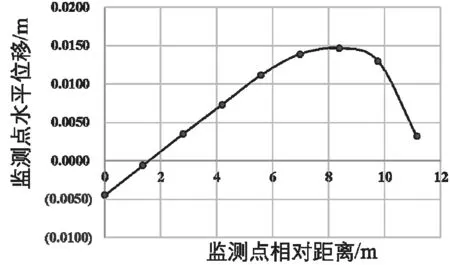
图4 迎水面水平位移变化趋势
为同时分析整个开挖时呈内一级岸坡与二级岸坡的位移变化情况,将各自的顶点作为特征节点,将其水平位移进行输出,如图5所示。图5中,监测点1为一级边坡顶点,监测点2为二级边坡顶点。随着开挖的进行,两级边坡的顶点都产生了向左的水平位移,其中一级边坡水平位移当开挖到第2步时,出现拐点,此时变化速率达到最大,之后随着开挖的进行变化趋势逐渐放缓,说明开挖第2步之后,二级边坡的开挖对一级边坡的影响较小。而监测点2则在开挖到第6步时达到最大,其实这与图4中第8步坡角水平位移达到最大值的结论并不冲突,说明只监测坡顶位移的变化,虽有一定参考价值,但由于复合土层的物理参数各异,其结果并不能完全确定边坡的破坏趋势,还应该综合边坡内部其他点的变化情况来加以判断。
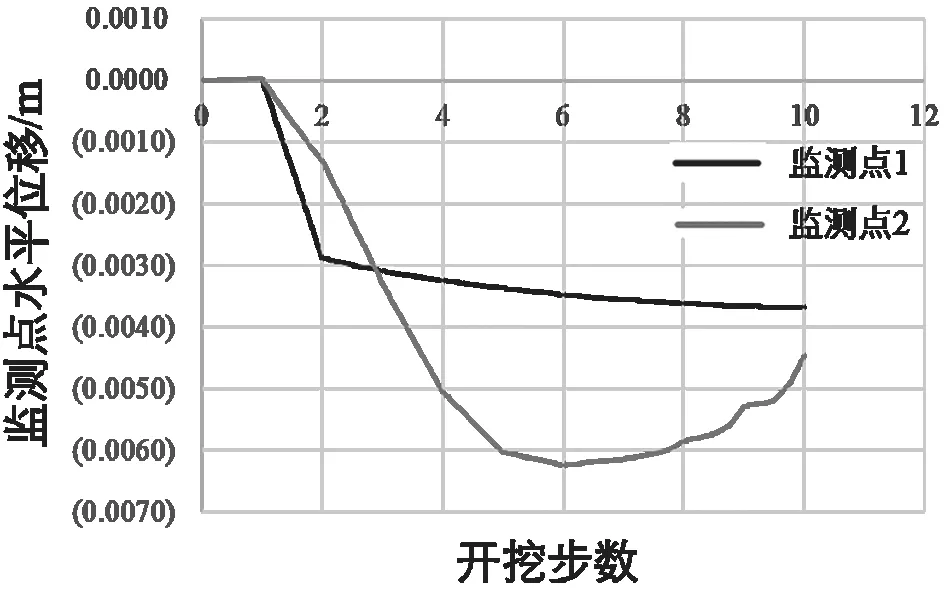
图5 监测点位移与开挖步数关系
3.3 卸荷过程坡体安全系数分析
为分析不同开挖步数结束后岸坡的稳定性系数,本次计算采用的是软件重启动技术,先将开挖后岸坡变形计算结果保存之后,在model-editatrributes选择重启动所需要的源文件。完成上述步骤之后,再制定读入数据的时间,并选择结束时间,此时就可对不同开挖步数结束后所形成的岸坡的稳定性系数进行分析。图6给出了开挖步数与岸坡安全系数关系。如图6所示,随着开挖深度的增加,边坡的安全系数逐渐减小,其中第一次放坡结束后,边坡安全系数为1.3,而第二次放坡结束后,稳定性系数降低为0.61。图7给出了本次河道施工结束后边坡的潜在滑动面(由于对称只画出河道左岸)。图7中贯通面通过了一级与二级岸坡坡体,其潜在剪出口距离最终设计高程1.28 m左右。

图6 开挖步数与岸坡安全系数关系
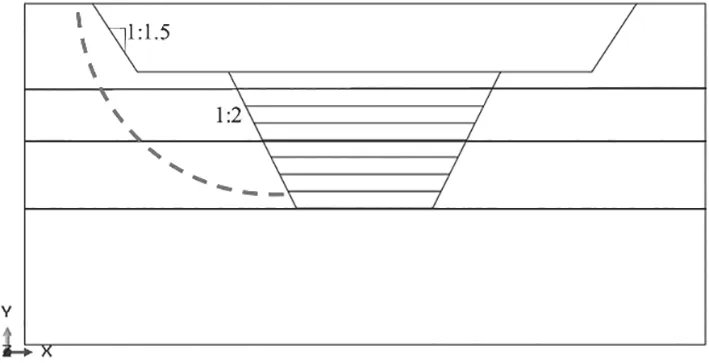
图7 开挖结束后边坡滑动面
4 结论
文中采用ABAQUS建立了2维河道开挖模型,在有限元方法基础上采用强度折减法,采用M-C模型分析了河道卸荷过程坡体的塑性应变、位移以及安全系数,主要得到了以下结果:
(1)应力历史对土体力学性质有着至关重要的作用,在第一次卸荷后,河道底部的塑性应变最大且范围最广,固结压力最大,应力路径的影响程度就越大。
(2)在第一次放坡结束后,在河道的亚黏土层产生了较大的向右的水平位移。第二次开挖所形成的边坡坡角具有较大的水平位移,但随着开挖深度的逐渐增加,河道左岸正水平位移的数值较大的范围逐渐减少。
(3)随着开挖深度的增加,边坡的安全系数逐渐减小,其中第一次放坡结束后,边坡安全系数为1.3,而第二次放坡结束后,稳定性系数降低为0.61。
