考虑热塑性变形的316H不锈钢Johnson-Cook本构参数逆向识别

李秀儒 魏兆成 郭明龙 王敏杰 郭 江 高 伟 孙 昉

1.大连理工大学精密与特种加工教育部重点实验室，大连，1160242.陆军装备部大连军代室，大连，116010

0 引言

316H不锈钢因其优异的高温力学性能和耐辐照性能、优良的可焊性、较小的热膨胀系数，而成为第四代核电站关键装备的主要材料[1-2]。但从机械加工角度来看，316H不锈钢的切削加工性能较差，在切削过程中会出现切削力大、切削温度高、切屑不易折断、刀具磨损较快、加工硬化严重等问题，是一种典型的难加工材料。因此，研究316H不锈钢的切削机理对优化工艺参数、提高加工质量和生产效率、促进其在核电装备中的大规模应用具有重要意义。

目前，国内外学者对316H不锈钢蠕变变形的组织演变和损伤等进行了大量研究[3-4]，对材料处于剧烈变形状态的切削过程研究较少，缺乏材料的动态力学性能参数限制了材料在某些关键零部件中的应用。在316H不锈钢切削过程中，工件在刀具的挤压剪切作用下发生剧烈变形，而本构模型是描述此过程的关键，其精度对机械加工中切削力、切削温度及表面质量等的精确预测具有决定性作用。目前常见的本构方程分为经验型[5-7]和物理型[8-10]。Johnson-Cook(J-C)模型综合考虑了材料应变硬化、应变率强化和温度软化效应的影响，且模型中的参数容易通过实验获取，而被广泛用于研究切削加工中材料的力学行为。

J-C材料本构参数的获取方法主要有三种：有限元法、霍普金森压杆试验法和切削试验法。SHROT等[11]提出了一种基于Levenberg-Marquardt搜索算法的J-C本构参数有限元识别方法，该方法虽然可以获得 材料的本构方程，但是需要进行大量的计算、耗费大量的时间。霍普金森压杆试验法是获取J-C本构参数最直接的方法。国内外学者采用霍普金森压杆试验得到了很多材料的本构方程[12-13]，但是该方法只能研究金属在应变率为103～104s-1的本构关系，对切削过程中的大应变(大于1)、大应变率(103～106s-1)和高温的热塑性变形行为还是难以准确描述。切削试验法通过金属切削理论求解出切削区域的应力、应变、应变率和温度，从而反向识别J-C本构参数，该种方式可较为准确地描述切削区的变形情况。TOUNSI等[14]建立了不等分剪切区模型，并结合正交切削试验逆向识别了316L不锈钢的本构参数。潘鹏飞等[15]、陈冰等[16]基于切削理论，逆向识别了不同材料的J-C本构参数，该方式可以一次性识别5个参数，但需要预先知道参数的大致范围，否则将大大增加辨识时间。

本文旨在解决316H不锈钢本构参数缺失和传统霍普金森压杆试验无法准确描述切削加工中材料热塑性变形行为的问题，提出一种基于切削理论的材料Johnson-Cook本构参数逆向识别方法。根据不等分剪切区模型建立主剪切区的应力、应变、应变率及温度分布模型，进行正交切削试验和准静态压缩试验，通过粒子群算法逆向识别了316H不锈钢的J-C本构参数，将获得的本构模型代入基于不等分剪切区模型的切削力预测模型，并验证该逆向识别方法的可行性和316H不锈钢本构模型的可靠性。

1 剪切区模型

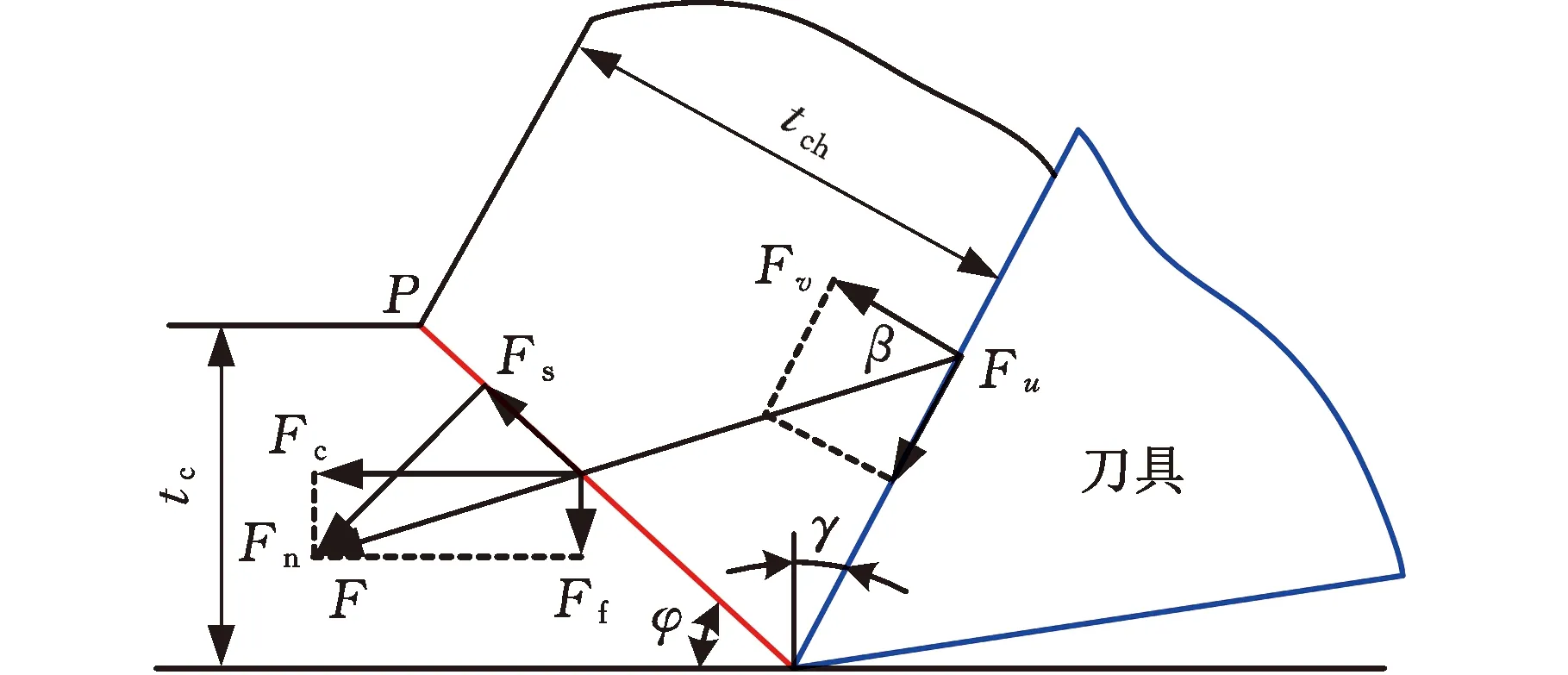
金属切削理论中，传统剪切区模型通常用直线代替塑性变形剪切边界线，认为剪切区是一个没有厚度的单一平面，如图1a所示。随着对剪切区研究的进一步深入，学者们逐步考虑剪切区厚度的影响并提出平行剪切区模型，如图1b所示。图1中，tch为切屑厚度。本节基于MERCHANT[17]的单一剪切面模型、OXLEY[18]的塑性剪切理论、ASTAKHOV等[19]的不等分剪切区理论，给出了不等分剪切区的应力、应变、应变速率和温度的表达式。

(a)单一剪切面模型

由单一剪切面模型(图1a)的几何关系可得前刀面上的摩擦力Fu和压力Fv，以及剪切平面处剪切力Fs和法向力Fn如下：

(1)

(2)

式中，γ为刀具前角；φ为剪切角；Fc为沿切削运动v方向的力；Ff为垂直切削运动v方向的力。

利用切削试验方法获得的摩擦角β与测量力的关系为

(3)

剪切角是切削速度与主剪切面的夹角，反映切削变形的大小。根据MERCHANT[17]的最小能量理论可得切削模型中的剪切角为

(4)

根据正交切削理论，主剪切面的剪切应力为

(5)

式中，tw为切削宽度；tc为切削厚度。

联合式(5)、式(2)可得

(6)

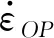
(7)

(8)

其中，η为不确定系数，它描述了剪切区中切向速度的非一致性，其大小与材料属性和切削状态有关；h为剪切区厚度。SHI等[20]发现，η=4时，式(7)可以很好地描述剪切区的应变率分布。

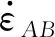
(9)

式中，v为主切削速度。

将主剪切平面的切向速度vy|x=ah=0代入式(9)可得

(10)

(11)

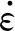
(12)

因此，主剪切面OP的剪切应力为

(13)

根据Mises准则计算主剪切区OP的等效应力、等效应变、等效应变率：

(14)

将工件看作半无限体，则正交切削过程中的切削传热可简化为二维传热问题。通常认为剪切区处于绝热状态，可忽略热传递；剪切区热量仅由塑性变形引起，可忽略主剪切区的摩擦。根据OXLEY[18]的切削理论和LOEWEN等[21]提出的切削温度模型，可得主剪切面处的平均温度为

(15)

(16)

式中，θ0为材料的初始温度；Δθ为绝热温升；kc为材料的热导率；c为材料的质量热容；ρ为材料的密度；R1为剪切面产生热量流入切屑的比率[22]。

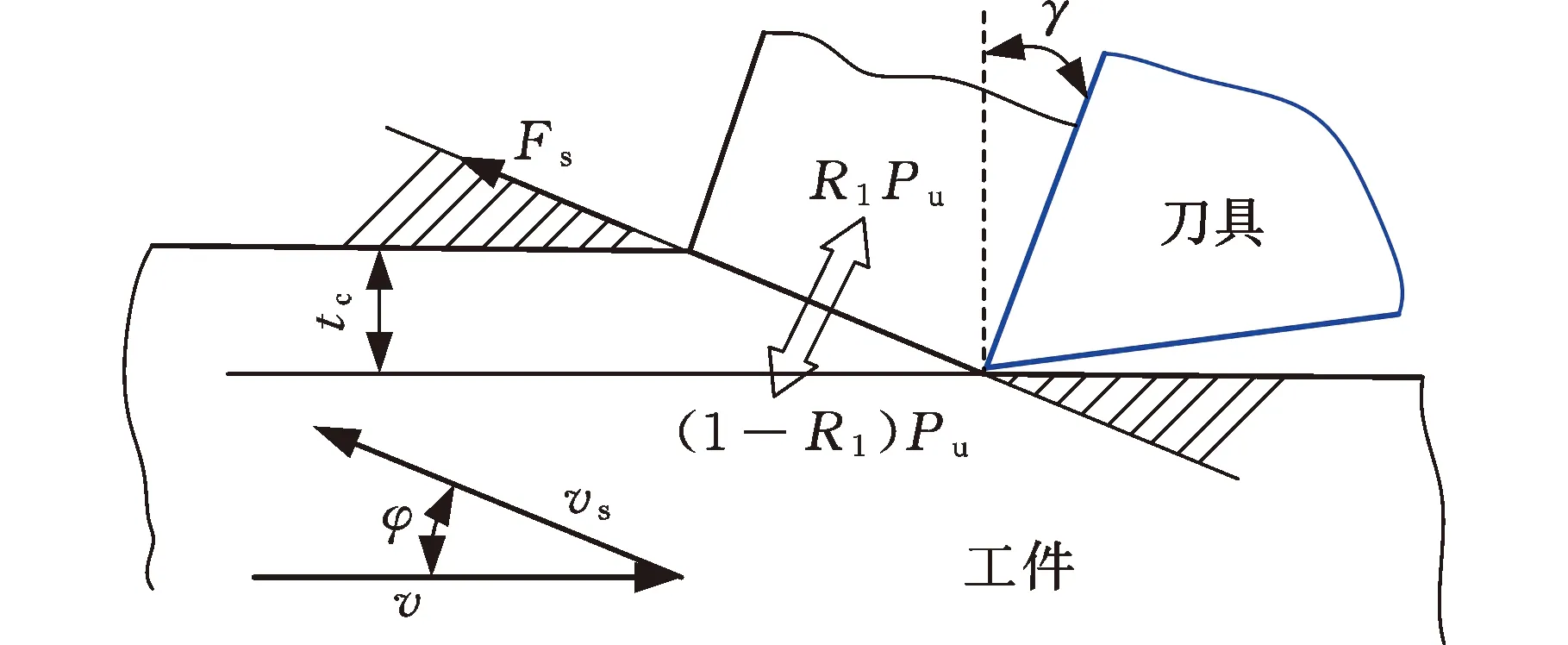
图2 剪切区温度分析

2 316H不锈钢本构参数识别

J-C本构模型是针对材料大应变、高应变率、高温等提出的材料本构模型：

(17)

该模型能综合描述材料的应变强化、应变率强化和温度软化效应。由于切削过程中涉及大应变、高应变率和高温，因此，该模型经常被用来描述切削加工过程中的材料力学行为。

2.1 本构参数识别方法

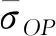
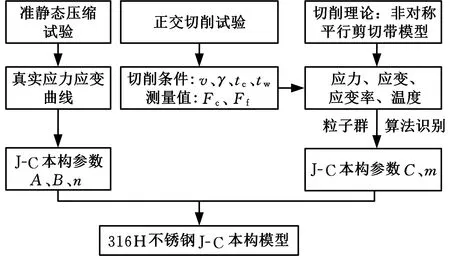
图3 316H不锈钢本构参数识别思路

(18)

根据设定的参数范围进行优化拟合，获得316H不锈钢J-C本构的最优参数C、m。

2.2 316H不锈钢材料成分

本文试验用316H不锈钢的材料成分及其质量分数如表1所示。

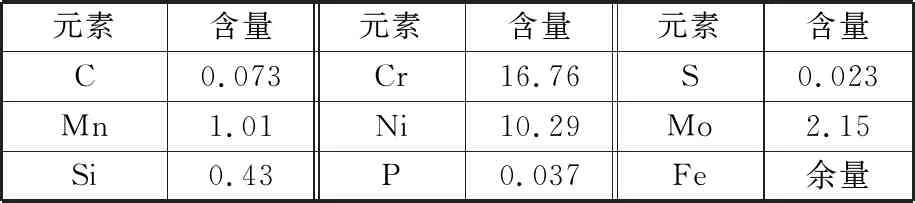
表1 316H不锈钢的化学成分(质量分数)

2.3 准静态压缩试验

准静态压缩试验在MTS静态万能材料试验机上进行，316H不锈钢试样尺寸为φ5×5 mm，试验温度为20 ℃，压缩速率为0.5 mm/min。将试验获得的压力和位移处理后，绘制材料的真实应力-应变曲线，如图4所示。

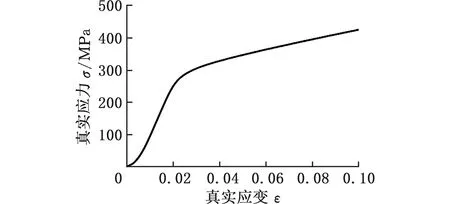
图4 准静态316H不锈钢真实应力-应变曲线

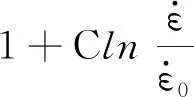
σ=A+Bεn

(19)

将式(19)变换并取对数，可得

ln(σ-A)=nlnε+lnB

(20)

将真实应力-应变曲线转换成ln(σ-A)-lnε曲线，取该曲线塑性变形部分的斜率和截距即可得到B=1069.5 MPa，n=0.7861。

2.4 正交切削试验

正交切削是指刀具主切削刃与切削速度方向垂直，刀具只承受切削方向的水平分力和垂直分力，切削状态属于二维切削。正交切削试验采用沈阳机床厂的CA6140卧式车床。试验工件为316H不锈钢棒料，试验之前加工成图5所示形状，工件外径200 mm、环宽2 mm。刀具选用三菱硬质合金刀片TCMW16T304HTi10，刀片前角0°，后角11°，刀柄具有5°前角，使得实际刀具前角为5°。切削过程中的主切削力和进给力采用大连理工大学研制的YDCB-Ⅲ05型三向压电石英测力仪获取。

(a)正交切削试验现场图

笔者进行了大量的切削试验，以期能够涵盖正常切削过程中出现的应力、应变、应变率状态，试验切削参数及测量结果如表2所示。

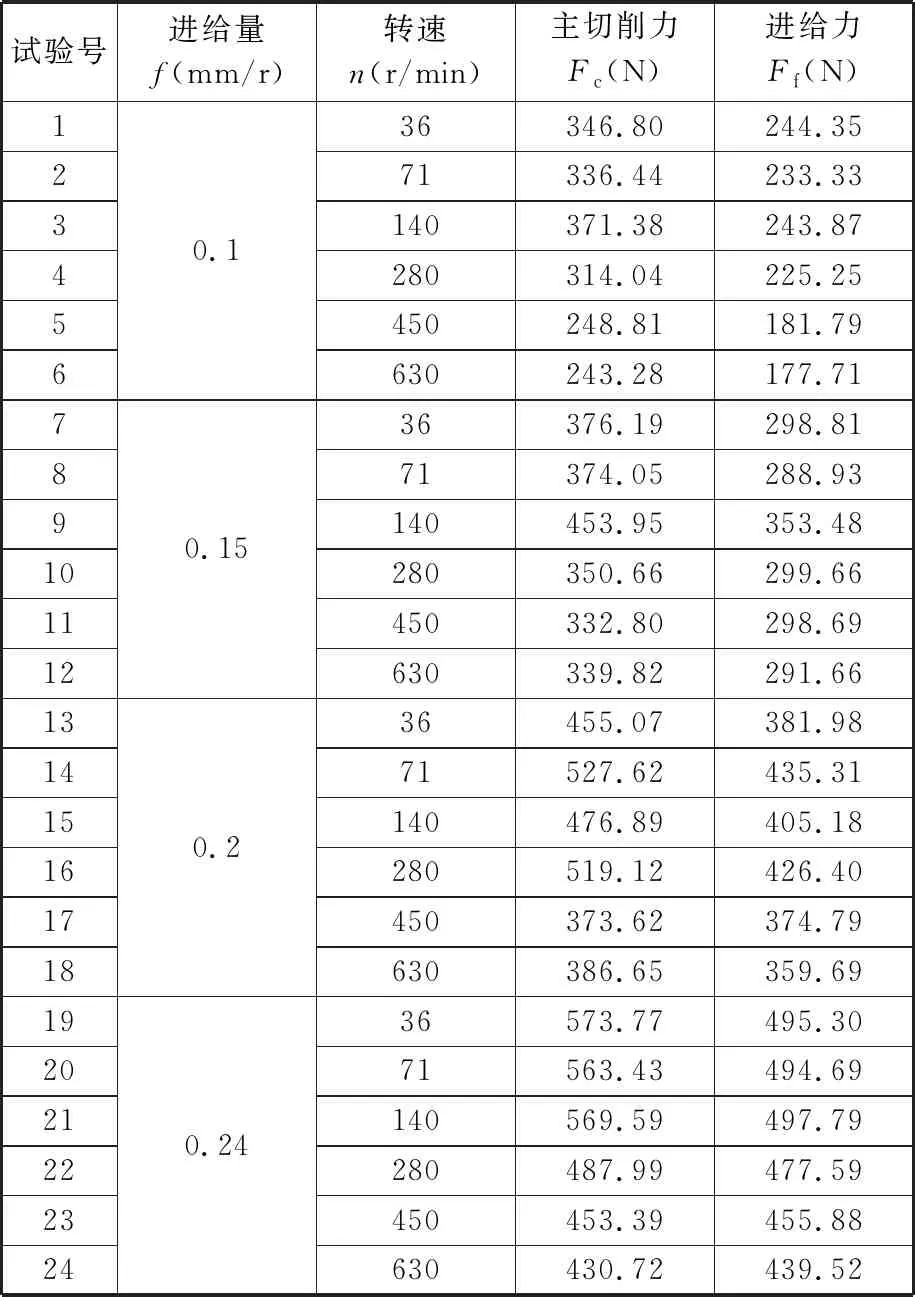
表2 316H不锈钢正交切削试验参数及测量结果

2.5 基于粒子群算法的J-C本构参数识别

非线性拟合较多采用以最小化误差平方和的最小二乘法，此方法可以较为方便地求出未知参数，但J-C本构模型涉及非线性拟合问题，传统的大范围搜索算法不仅耗时耗力、识别精度不高，而且很有可能落入局部最优解。粒子群算法是一种

基于群体智能理论的优化算法，通过群体中个体间的协作和信息共享来寻求优解。与一般现代进化算法相比，该算法是一种高效的并行搜索算法，概念简单，容易实现，而且可防止陷入局部最优解[23]。因此，本文采用粒子群算法对J-C本构的应变率强化系数C和温度软化系数m进行搜索拟合，图6是粒子群算法的流程图。

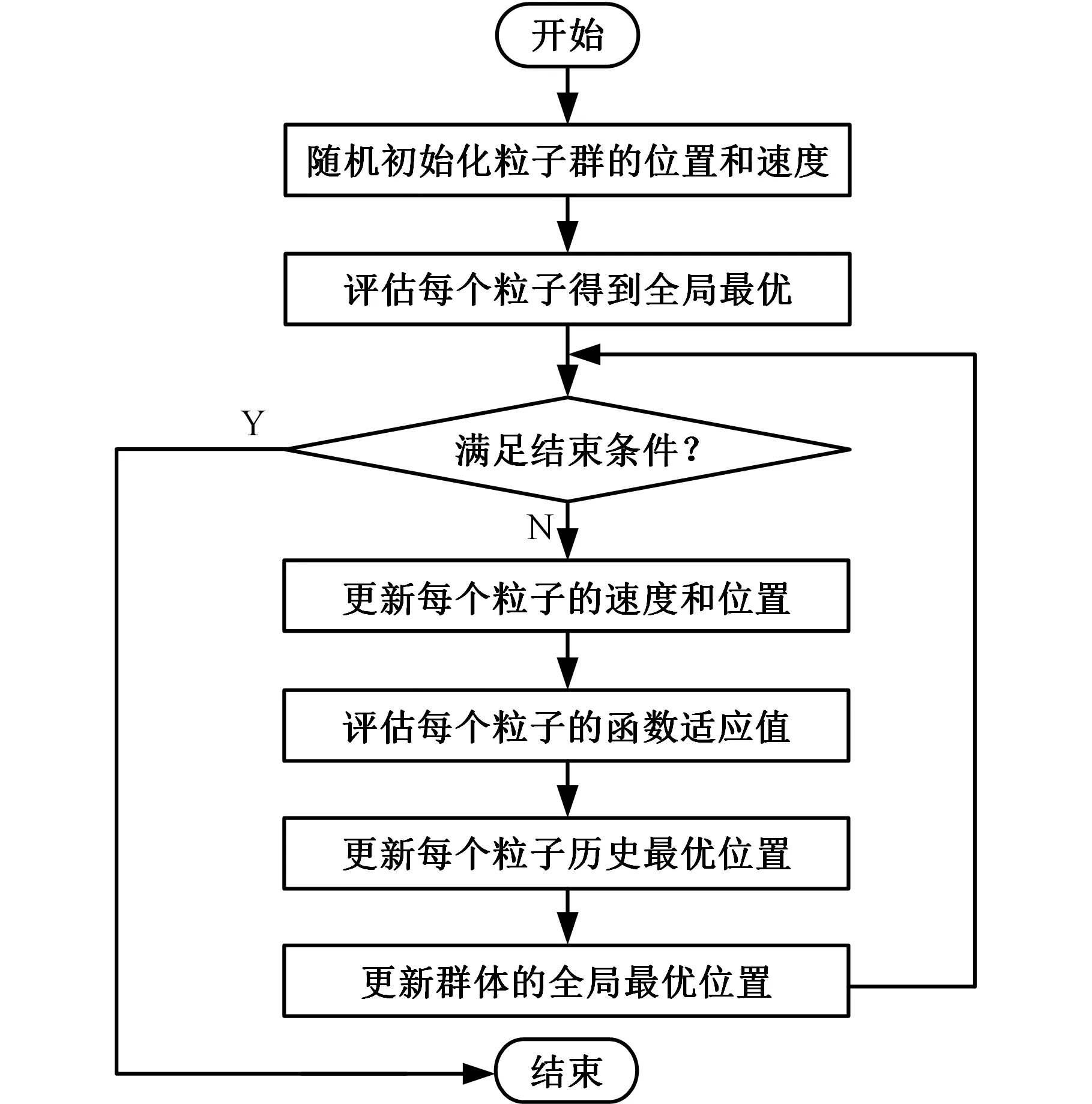
图6 粒子群算法的流程图

要想在粒子群算法中获得最优解，就需要预先设置参数范围。现有文献还未出现对316H不锈钢J-C本构方程的研究，因此本文选取316L不锈钢的本构方程来确定参数的大致范围：-2≤C≤2，-2≤m≤2。本文中的适度函数采用式(18)，适度值为每次迭代的结果。种群的粒子数为20，维数设为2，学习因子设为2，初始惯性权重设为0.9，算法容忍度为10-6，迭代进化次数为200，在MATLAB 2016b上进行编程计算。由图7可知，J-C本构参数搜索的适应度随迭代次数增大而逐渐减小，并在迭代29次后逐渐稳定，最终得到C=-0.0124，m=0.425。

图7 适度值随迭代次数变化趋势

综上所述，通过准静态压缩实验和正交切削试验最终识别出316H不锈钢本构模型参数：A=285，B=1069.5，n=0.7861，C=-0.0124，m=0.425。J-C本构方程表达式为

3 316H不锈钢本构模型的验证

为验证建立的本构模型的有效性，基于不等分剪切区模型建立切削力预测模型，从切削力角度验证316H不锈钢本构方程，其计算路线如图8所示。

图8 基于不等分剪切区模型的切削力计算路线

3.1 刀-屑摩擦因数拟合

摩擦因数对剪切角和剪切力的计算有较大影响，一般情况下将摩擦因数看成常数，但研究表明摩擦因数与工件材料、刀具前角、切削速度和切削厚度有关。因此，根据不同切削速度和进给量下的正交切削试验获得的摩擦因数绘制成图像，观察其随切削条件变化的规律。由图9可知，摩擦因数随切削速度变化基本无变化，但摩擦因数随进给量的增大而逐渐减小。因此，将摩擦因数拟合成关于进给量的表达式较为合理，关系式如下：

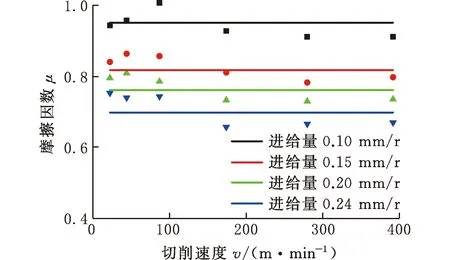
图9 316H不锈钢切削过程中摩擦因数

(21)

另外，已有研究[24-25]表明摩擦因数与刀具前角成线性关系，因此针对-6°和0°刀具前角分别进行了多组切削试验，切削参数与表2相同。根据试验结果拟合了316H不锈钢摩擦因数与刀具前角的关系：

μ=0.02274(γ-5)+μ0

(22)

3.2 试验验证

本文选取18组不同的刀具角度、切削速度和进给量进行预测和正交切削试验，试验条件、预测结果和试验结果如表3所示。由表3可以看出，主切削力和进给力的预测值与试验值的最大误差为13.64%，说明本文建立的本构模型可较为准确地描述316H不锈钢实际切削加工中的材料变形，模型具有较高可靠性，也验证了该逆向识别方法的可行性。与现有的逆向识别方法[11，14-16]相比，采用准静态压缩试验可准确获取材料静态力学数据，进而精确地拟合参数A、B、n；采用正交切削试验并结合不等分剪切区模型的方式，能更加准确地描述材料动态变形过程，保证了逆向识别数据C、m的合理性和准确性。与采用有限元方法逆向识别和一次识别出全部J-C本构参数相比，采用粒子群算法识别C、m提高了计算效率和计算精度。

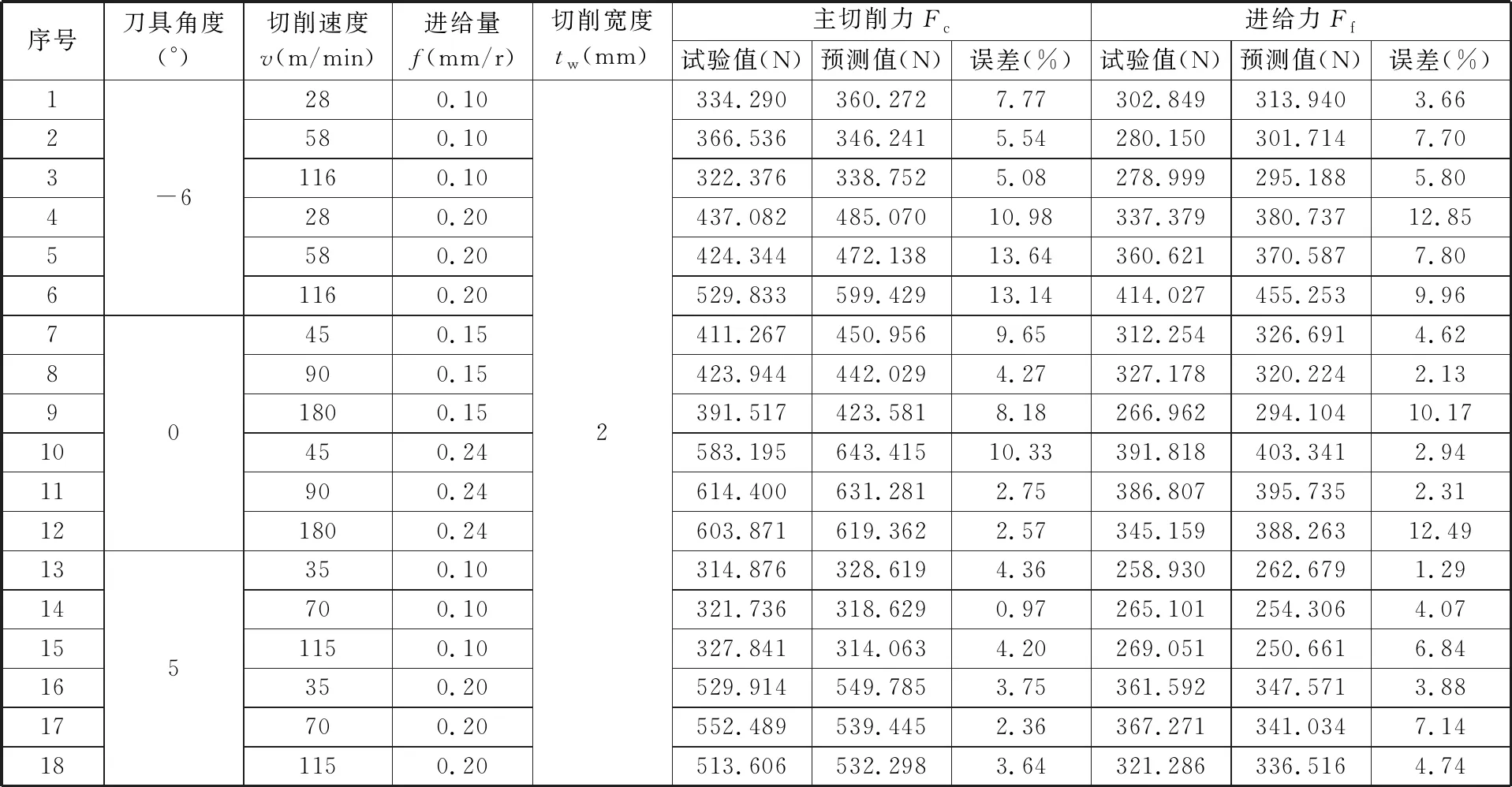
表3 316H不锈钢正交切削试验与模型预测结果对比

4 结论

(1)针对316H不锈钢动态力学性能参数缺失和传统霍普金森压杆试验无法准确描述切削加工中材料热塑性变形行为的问题，提出了一种基于不等分剪切区模型的材料J-C本构参数逆向识别方法。

(2)利用准静态压缩试验直接获取了316H不锈钢室温时的屈服应力、应变强化系数和加工硬化指数，利用正交切削试验数据逆向识别了应变率强化系数和温度软化系数，最终获取了316H不锈钢的J-C本构模型。

(3)将摩擦因数拟合为关于刀具前角和进给量的表达式，提高了切削力预测精度。

(4)根据获得的316H不锈钢J-C本构模型，利用基于不等分剪切区的切削力预测模型预测了切削力，切削力预测结果与试验结果的最大误差为13.64%，验证了本构参数的可靠性和逆向识别方法的可行性。