物理问题的数学建模例析——基于云南省2021年中考物理第18题的反思

张云刚

（云南省德宏州民族初级中学，云南 芒市 678400）

许多物理问题一旦转化为用数学模型来处理，就变得目标明确、思路顺畅，因此它是一种很重要的思维方法，在物理学中运用广泛.物理问题的数学模型的建立，都大致经过以下几个主要步骤：物理原型的分析、物理原型的简化、数学模型的建立.

1 物理原型的分析

对物理原形的认真研究和分析，是建立数学模型的第一步，主要经历以下几个步骤.

（1）确定所要研究的物理系统.物理学系统中，又可具体地分为力学系统、热学系统、电磁学系统等，而适用于每一种具体物理系统的数学理论和方法是不同的，因此也就对应于不同的数学模型.

（2）了解物理原型的基本特征.了解物理原型的基本特征，有利于数学理论和方法的选择.

（3）确定物理原型的基本描述量.数学模型反映的就是系统中各物理量之间的数量关系，所以确定基本描述量对建立数学模型是十分重要的.

2 物理原型的简化

任何一个物理原型都是由各种复杂因素共同构成的，这些因素彼此关联，共同处于一个运动、发展和变化的体系之中.简化物理原型，就是要忽略次要因素，抓住主要因素；就是要忽略各因素之间的次要关系，而突出它们之间的主要关系.

物理原型的简化过程，实际上是对物理原型进行简单化、理想化处理的过程，是一个质的抽象的过程，是一个抓主要矛盾的过程.不经过这个过程，考虑的因素太多，各因素间关系过于复杂，根本就无法建立简洁实用的数学模型.

3 数学模型的建立

建立数学模型，首先要根据物理原型的性质选择相应的数学理论.其次是要将所选择的数学工具与已有的物理规律紧密结合起来.第三是要合理巧妙地运用数学方法.

以上简要地论述了建立物理问题的数学模型的3个主要步骤.在实际的应用中，3个步骤之间并不存在明显的界限，它们是相互交叉、相互影响的整体工程.本文以2021年云南省中考物理第18题为例，分类说明建立物理问题转换数学模型的运用及步骤.

3.1 利用数学函数研究物体的运动规律

首先，根据物体的受力情况可以确定物体的运动状态.我们知道重力是质量的一次函数；质量是体积的一次函数……反之亦然，故如果确定了物体的运动状态，就可以得出物体的受力情况，这样一来对确定物体运动规律之类的物理问题就转化为求物体的状态量与物质特性的函数关系问题.

例1.（2021年云南卷）如图1所示，水中有一支长14 cm、底部嵌有铁块的蜡烛，露出水面的长度为1 cm.点燃蜡烛，至蜡烛熄灭时，对水容器底部产生的压强_________（选填“变大”、“变小”或“不变”）.熄灭时蜡烛所剩长度为_________cm.（ρ蜡=0.9×103kg／m3）

图1

物理原型：合力概念.物理原型的分析：① 蜡烛长度为h刚点燃时，处于漂浮状态如图2所示，蜡烛所受合力为零.蜡烛燃烧过程中引起质量变化，而影响到蜡烛在液体的状态，这些作用中，蜡烛所受的重力作用是蜡烛运动状态变化的根本动力，起着决定性的作用，而铁块的重力、浮力不变可以忽略.这样，研究的系统就可以确定为“蜡烛、水”二体力学系统.② 原型的基本特征.蜡烛燃烧掉长度为L刚熄灭时，剩余蜡烛处于悬浮状态如图3所示，是可以准确确定和预测的，属于物体系的规则运动.③ 确定基本描述量.蜡烛两次运动状态与所受的重力、浮力有关，因此蜡烛的质量m、蜡烛排开水的体积V排是基本描述量，并且蜡烛从开始点燃到熄灭m、V排是变量，剩余蜡烛的长度h-L即为待求的量.

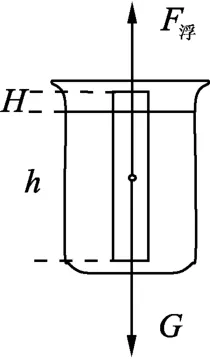
图2

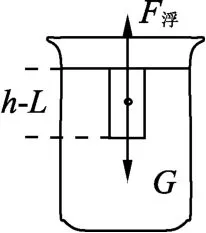
图3

物理原型的简化：① 确定二体力学系统.这实际就已经对物理原型进行了简化，即排除了铁块的影响，突出了蜡烛的关键作用.② 忽略燃烧了的蜡烛，只考虑剩余蜡烛.③ 忽略蜡烛和剩余蜡烛的大小，把蜡烛和剩余蜡烛抽象为质点.这样，物理原型就简化为两个质点的运动状态了.

数学模型的建立：因为蜡烛与水静止是有确定性因果关系的运动，所以通常选用经典数学理论所提供的方法.第2空演算过程如下.

解析：设蜡烛长度为h，刚点燃受力分析如图2所示.

因为漂浮，故F浮=G总，

设燃烧掉蜡烛长度为L，刚熄灭受力分析如图3所示，

因为悬浮，故F浮=G总.

由（1）-（2）式得

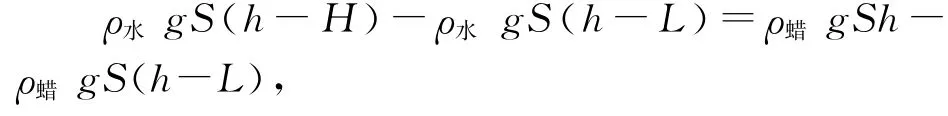
整理得H／L=（ρ水-ρ蜡）／ρ水.

这个方程，即为我们要建立的蜡烛漂浮水面的数学模型.即H／L的关系.

数学模型建立后，就可以用纯数学的方法，在考虑“初始条件”和“边界条件”的情况下对方程求解.这是一个L与H的函数，蜡烛对应的运动状态状态是刚点燃时漂浮和刚熄灭时悬浮.通过计算可以确定底部嵌有铁块的蜡烛，任意露出水面长度为Hcm（H≤h／10，H大小由嵌铁质量调节）时刻燃烧至熄灭剩余蜡烛长度.

当H=1 cm；L=10 cm.

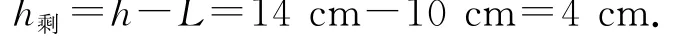
点评：本题涉及的知识主要有受力分析、二力平衡条件、阿基米德原理、物体的浮沉条件等.从知识体系看，这些内容都属于核心知识，而且与高中学习关系密切，重基础可持续学习.要求学生搞清漂浮蜡烛燃烧过程中，它的质量在减小，浮力也会减小，它会逐渐露出水面.特别是漂浮蜡烛燃烧时，会将蜡烛芯附近的蜡熔化，外面的一层蜡因为水的冷却不会熔化.随着蜡烛不断燃烧，蜡烛芯的位置越来越低，烛火就慢慢燃烧到水面下约1.8 cm左右，于是出现了如图4所示“水火相容”的景象.最终，如图5所示边缘的蜡烛也会熔化，水便将蜡烛冲灭，剩余蜡烛在水中悬浮.

图4

图5

本题要抽象出燃烧蜡烛漂浮、悬浮模型，对学生实验理解能力的要求很高，要运用纯字母运算建立数学模型才能求解.整个题目求解思路灵活、方法多样，区分度很高，成为本卷“热点”.深剖本题提炼出解决初中物理力学问题常用程序：（1）确定研究对象，进行运动和受力分析；（2）分析物理过程，按特点划分阶段；（3）选用相应规律解决不同阶段的问题，列出规律性方程；（4）找出关键性问题，挖掘隐含条件，根据具体特点，列出辅助性方程；（5）检查未知量个数与方程个数是否匹配；（6）解方程组.

3.2 用数学函数定量（定性）分析物理量的变化

物理问题中经常遇到某一物理量变化导致其它一些物理量的变化问题，这些问题的实质用数学分析的观点来看属于讨论函数y=f（x）中x发生变化y如何变化的问题.

例如例1中的第1空解析如下.

解析：设蜡烛长度为h，刚点燃受力分析如图2所示.

因为漂浮状态，故F浮=G总.

燃烧蜡烛时G总变小，F浮变小，V排变小，h水变小.

ρ液=ρ水g h水=＞ρ水、g不变，h水变小，则ρ液变小.

3.3 用数学函数极值问题

极值问题是中学物理难点，解决这类问题的常用思维方法是建立所求极值的物理量与变量之间的函数关系式，在一定条件下求函数极值.

例2.（2020年云南卷）实验后，小明将一支5Ω的定值电阻与“标有20Ω 1 A”的滑动变阻器串联在电压恒定为3 V的电源上，请你帮助小明计算出滑动变阻器的最大功率为_______W.

对比例1（1）、例2两题，异同点见表1.中考试题是命题专家团队集体智慧的结晶，也是全省考生和教师的一次学习成果和教学的检验，无疑是教师教学的最佳素材，也是今后教学工作和研究的风向标.纵观近几年的云南省中考物理试卷，其中力、电内容向高中物理“渗透”的部分逐年增多，通过两道题对比分析，现在的“压轴题”不仅需要具备扎实的数学知识，而且还要具有巧妙解决具体问题的数学能力.因此，教师在物理教学过程中应强调数学思想的运用.

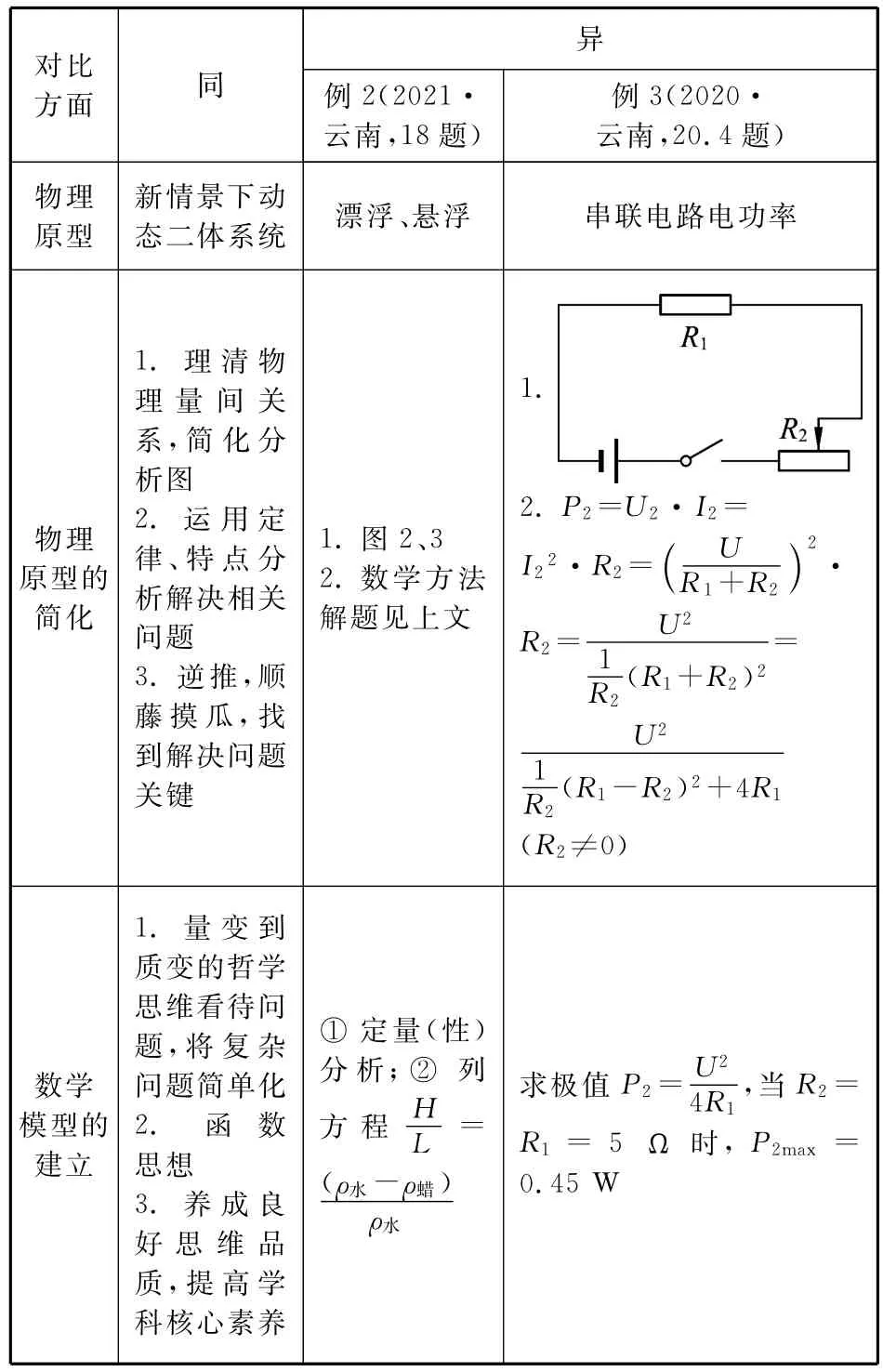
表1