基于标签传播的两阶段社区检测算法

孙学良，王巍，黄俊恒，辛国栋，王佰玲

（1. 哈尔滨工业大学计算学部，黑龙江 哈尔滨 150001； 2. 哈尔滨工业大学（威海）计算机科学与技术学院，山东 威海 264209）

0 引言

网络是表示事物与事物之间联系的常用工具。现实生活中，各个组织随着时间推移所产生的复杂信息常以网络的形式呈现，如科研协作网、社交关系网、金融交易网络等。在这些网络中，通常存在很多自然形成的社区，社区内部成员与成员之间联系紧密，社区之间联系稀疏。如何有效地从网络中识别出这些社区是社区检测的基本任务，具有重要的现实意义。例如，从科研协作网中识别出具有相近研究领域的学者，或者从社交网络中识别出具有相似兴趣爱好的用户等。

随着复杂网络研究的深入，相当多的社区检测算法被相继提出，许多算法从不同角度来解决社区检测问题[1]。最开始是分裂算法，它基于去除边的思想将社区分开，但这种全局的方法对计算要求很高。为了克服这个问题，研究人员后续提出了凝聚算法或其他优化算法进行改进。在优化算法方面，基于模块度的算法成为优化算法的主流，但基于模块度的算法不易发现小的社区，计算量过大，因此后续发展出其他的解决方案。

2007年，Raghavan[2]提出的标签传播算法（LPA，label propagation algorithm）就是其中的代表方案，LPA因其易于实现、概念简单广受欢迎，该算法受传染病模型的启发，通过节点标签的迭代更新直至收敛来检测社区，但算法存在随机性强、运行结果不稳定等问题。

为了使社区检测更加真实地反映节点和社区之间的实际关系，本文在标签传播算法的基础上，消除了原算法的不稳定性，并采用矢量表示和广度优先传播的思想，对标签的传播策略进行了改进，主要工作如下。

1) 提出了基于标签传播的两阶段社区检测算法（TS-LPA，two-stage community detection algorithm based on label propagation），重点优化了标签更新过程。

2) 结合网络局部拓扑结构信息，本文采用扩展邻域的思想对节点的中心性进行度量，并在此基础上提出一种新的评价指标来衡量节点之间的影响概率。

3) 利用广度优先传播的思想，提出了第二阶段标签传播方式，来提高社区检测的质量。

4) 在不同数据集上的实验结果表明，TS-LPA表现出较强的稳定性，有效提高了社区检测的质量。

1 相关工作

国内外学者在定义、检测和识别现实网络的社区方面做了很多工作，提出了各种算法，根据社区检测的“方向”，可以分为自上而下的方法和自下而上的方法[3]。

自上而下的方法：基于图或者边去除的思想，将整个网络分成小组，以检测社区。分裂算法属于该类别。2012年，Prat-Perez等[4]提出了一个加权社区聚类算法（WCC），并认为好的社区是在所有的社区节点之间形成大量的三角形社区，因此，为了定义社区，WCC测量节点x与集合S中的节点形成的三角形的比率，而不是x在整个图中形成的三角形的数量。2018年，Qiao等[5]提出了Picaso的自上而下策略，根据社区的特征，有些边的权重会消失，有些边的权重像山峰一样升起。算法包含两个阶段（山模型的构建和社区合并更新），经过实验分析表明，Picaso算法可以处理大型的网络，并且具有良好的 效率。

自下而上的方法：从局部结构开始扩展到整个网络，在这个过程中，逐步形成各种社区[6]。许多不同的想法实现了自下而上的检测方法，如模块度优化[7-9]、标签传播等。模块度优化是找到一个从指定节点开始的子图，使子图增加一个节点或者删除一个节点都会降低模块度值，最终找到的社区满足模块度值最大，实现社区的检测[10]。2004年，Newman首先定义了模块度概念并提出模块度算法[11]，之后提出Louvain算法，该算法在模块度算法基础上做了进一步的改进[12]，将层次聚类与模块度优化有效结合，分为两个阶段进行迭代划分检测。Louvain算法被认为是当前较为高效的社区检测算法之一；标签传播的基本思想是利用样本间的关系建立完全图模型，将图模型中每个节点作为中心节点进行迭代标签更新，迭代过程中利用一阶邻居标签对中心节点的标签进行更新。2007年，Raghavan等[2]将标签传播思想引入社区检测任务，提出了标签传播算法，该算法仅以网络结构为指导，每个节点都用一个唯一的标签初始化，并且在每一步每个节点都获得了它的大多数邻居当前拥有的标签。通过不断迭代，密集的节点组倾向于获得相同的标签，从而形成一个社区。该算法具有线性的时间复杂度，更适用于社区结构已知的网络。但是LPA算法也存在稳定性较差的问题，其示意如图1所示。

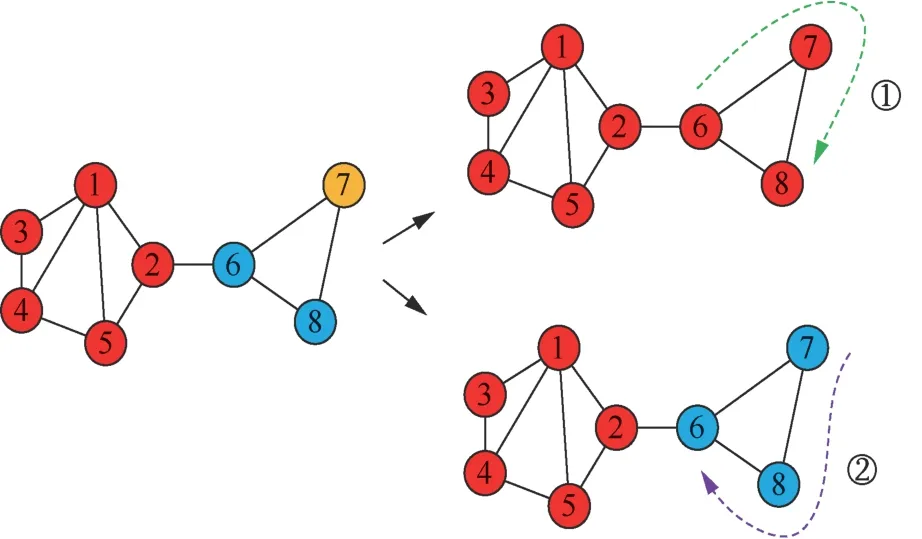
图1 标签传播算法示意 Figure 1 Schematic diagram of label propagation algorithm

从图1可知，根据节点更新顺序的不同，分别按照①号线条和②号线条更新时，产生的社区检测结果不同。例如，当标签按照①号线条传播时，节点标签更新顺序为6、7、8，6号节点邻居的标签分别为黄色、红色、蓝色节点各一个，在不同类别邻居标签数量相同的情况下，6号节点随机选择了红色，造成最终整个社区全都为红色节点。此外，在更新策略方面，同步更新可能引起标签震荡的问题，也会造成算法的不稳定[13]，其结果如图2所示。

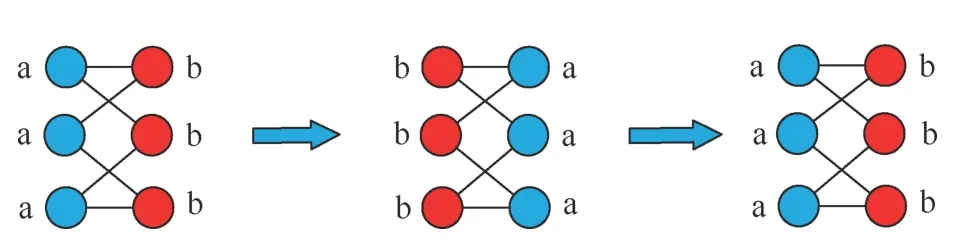
图2 人工网络同步更新的结果 Figure 2 Schematic diagram of manual network label synchronization update

后来，研究人员在LPA的基础上做了不同程度的优化，来适应更多的应用场景[14-18]：为了避免LPA将所有节点划分到同一社区，Barber和Clark[19]提出了一种模块化标签传播算法（LPAm），将社区检测问题转化为求目标函数最大值问题，但容易陷入局部最优解的情况。为了解决上述问题，Liu等[20]在LPAm的基础上，融合多步贪婪凝聚算法，提出了基于模块度最大化的标签传播LPAm+，将多对社区融合，避免局部最大值的出现。Li[21]探索了在LPA的基础上引入方向性的方法，提出了约束定向的标签传播算法，将边的方向转化为边的权重，探索了定向化模块的划分，但并未考虑边自身的权重信息。Zhang等[22]提出了一种基于节点重要性和标签影响的算法，融合贝叶斯定理来计算节点的重要性，对节点的重要性进行了有效评估，但该方法只考虑了周围节点的信息，并没有融合边的信息，使标签影响能力的计算有所欠缺。

现有LPA的改进工作主要针对节点标签初始化、节点的标签选择策略、节点的标签更新顺序等方面进行改进，并没有考虑节点之间的影响。在网络中已有信息的利用上，也没有很好的策略。针对以上不足，本文提出了一种新的节点之间影响力计算方法，并引入广度优先传播的思想来有效利用已知信息。

2 TS-LPA

本文引入扩展邻域的概念来表示节点传播信息的能力（即节点的影响力），通过综合节点影响力和边的权重信息计算节点之间的影响概率，算法的基本思想概括如下。

1) 构建网络图，利用扩展邻域核心度的方法来计算节点的重要性，并根据网络的拓扑结构，综合利用邻居信息得到节点的影响力。

2) 结合节点影响力和边的信息计算单个节点对不同邻居的影响概率，并进行均一化表示，构建网络的节点影响概率矩阵。

3) 在节点的设置方面，根据节点的影响力确定种子节点选取策略，利用矢量来表示节点的类标签，提高迭代效率。

4) 标签迭代更新过程中，利用广度优先搜索方式搜索种子节点信息，根据搜索结果，对标签更新的类标签向量进行进一步更新。

2.1 节点影响力计算

现实中复杂网络的节点地位是不平等的，不同节点对网络结构和性能的影响可能会有很大的差异，网络的传播效应会受到一些重要节点的影响。例如，在传销的运作中，总经理、经理、主任、业务员等人员在组织运作过程中扮演着重要的角色。这种现实职位的重要性同样反映在交易网络中，总经理的账号往往周围邻居节点数更多或者边的交易金额、交易次数权重更大，更大限度地影响着网络的结构和性能。

结合现实的分析，为了更有效地对节点的重要性进行衡量，本文采用节点的扩展邻域核心度[23]来量化节点的传播能力，在此基础上，综合考虑节点与其邻居节点之间边的权重及邻居节点的度数，扩展得到节点综合影响力Node值。

定义1对于给定的网络G= (V,E)，其中表示网络的节点集，E表示网络的边集。节点综合影响力Node值的计算如式(1)所示。

其中，E Ncoreness(i)[23]表示节点i的扩展邻域核心度，Wij表示节点i与节点j之间边的权重，N(i)表示节点i的一阶邻居节点集合，dj代表节点j的度数。

2.2 节点之间影响概率的计算

LPA的节点标签选择策略具有随机性，造成了社区检测的不稳定。此外，考虑周围邻居节点对更新节点的影响时并未涉及节点权重和边权重的影响。如图3所示，A、C、D与B进行业务往来，A与B进行了5次业务往来，涉及金额10 000元，C、D和B各进行了1次业务往来，涉及金额500元，根据标签传播算法，节点B应该划入C、D所属的社区，但实际上节点A对节点B的影响概率更大，这显然与实际不符。

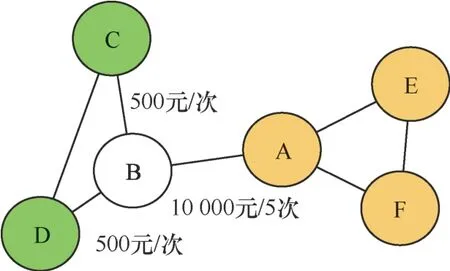
图3 一个人工生成的网络 Figure 3 An artificially generated network

为了解决此类问题，本文考虑邻居节点对待更新节点的影响，从节点的综合影响力、节点与邻居节点之间边的权重两方面来考虑，使待更新节点的所有邻居节点的标签都对其产生一定限度的影响，从而使待更新节点的影响因素多样化，提高节点标签更新的准确性。考虑到在实际应用网络（如传销金融网络）中，若利用交易平均金额来表示边的权值，不同边的权重可能在几百到几万之间不等，那么待更新节点的不同邻居节点影响力与边的权重的乘积会相差过大，不利于标签影响概率的计算。因此，本文在两者相乘的基础上，引入ln函数来弱化这种影响，利用百分比来表示节点对不同邻居的影响程度，使节点的标签对各个邻居节点都有一定限度的影响概率。综上所述，节点之间影响概率CL如定义2所示。

定义2对于给定的网络G=（V,E），节点之间影响概率CL值的计算如式(2)所示。

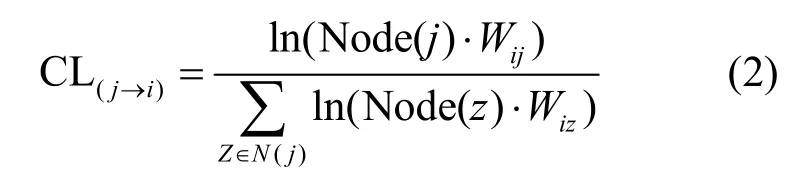
其中， CL(j→i)代表节点j到节点i的传播概率，N(i)表示节点i的一阶邻居节点集合，Wij表示节点i与邻居节点j之间边的权重。

2.3 节点的设置

在种子节点的选取方面，由于网络中节点的影响力具有明显的差异性，如何有效地选取网络中有影响力节点的问题显得尤为重要，选择网络中影响力大的节点作为种子节点有利于社区的形成与划分，能够将信息更好地传播到网络中，相反，如果选择影响力较小的节点，则不利于社区的形成，从而增加迭代次数，浪费算法的执行时间。

因此，本文在计算得到的节点的综合影响力的基础上，将节点综合影响力从大到小排序，构建节点影响力的排序表N，根据排序表N选取一定比例数据组成种子节点集合Seed。

在节点标签的设置上，本文利用标签向量来更详细地描述节点的社区类别信息。一方面，通过矢量化对节点的社区标签类别进行表示，这样在每一次的迭代中保证节点可能的社区类别标签都能够得到更新。如图4所示，节点3处于淡蓝色社区和紫色社区重叠地方，且两个社区对它的影响相差不大时，传统的标签传播方法在每一次迭代时只选择淡蓝色或者紫色一种作为类别，具有一定的绝对性，在使用矢量化表示后，3号节点社区类别标签则可以表示为（0.45,0.55）的形式，在每一次迭代时都能够对两个社区类别标签同时进行更新。

图4 具有两个社区的网络示意 Figure 4 Schematic diagram of a network with two communities

此外，经过若干次迭代后，两个社区对更新节点的影响差距逐渐变大，使节点的社区类别的确定更加明确。另外，节点社区类别的矢量化表示有利于提高算法的执行效率。

综上，节点社区类别标签的设置策略如下：设网络节点的集合为，其中，m(m≤n)个节点为已知标签节点，(n−m)个节点为未知标签节点，节点类别数c已知，定义一个c维的实值向量Ri∈Rc作为节点的标签向量，在标签向量初始化时，若节点vi为已知标签的节点，且该节点属于第p类，则Ri的第p维数值置为1，其余维度数值置为0。若节点vi为未知标签的节点，则Ri所有维度数值均置为−1，于是，问题转化为如何利用(vi,Ri)(1 ≤i≤m)的 数 据 预 测{vm+1, … ,vn}的标签数据{Rm+1, … ,Rn}。

将输入的数据进行处理，计算节点更新顺序、影响概率、节点标签等信息，并利用矩阵向量的形式进行存储，TS-LPA的数据预处理过程如下。

算法1TS-LPA的数据预处理过程

输入图G的邻接矩阵A，部分节点的标签

label

输出节点之间影响概率值CL，节点种子集合Seed，排序后节点影响力V_Sort，节点的初始化标签向量R_init

1) V_node = Node(A) //计算节点的影响力Node值

2) V_Sort = Sort(V_node) //根据节点重要性对节点进行

3) Seed = seedChoice(label,V_Sort)//选择种子节点

4) for ∀v∈V

5) for ∀u∈N(v) //对于节点v的所有邻居节点

2.4 节点标签的分阶段更新策略

LPA的不稳定性表现在算法更新过程中更新标签的选择，为了更好地利用邻居节点标签类别来进行标签更新，本文提出了两阶段更新 策略。

第一阶段：网络中每一个节点都有一个标签向量Ri，代表节点对于各个类别的隶属度，当算法开始传播的时候，待更新节点的所有邻居节点都对该节点的标签产生影响，邻居节点的标签向量Ri与节点之间的影响概率CL共同影响待更新节点的标签。设Li为第一阶段节点更新后的标签向量。第一阶段节点标签向量更新式如式(3)所示。

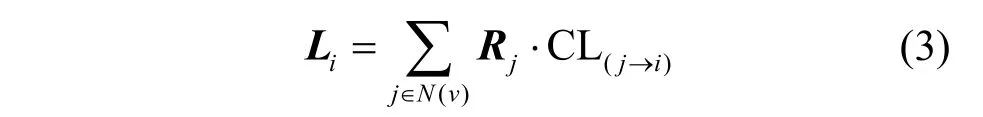
其中，N(i)表示待更新节点i的一阶邻居节点的集合，C L(j→i)表示节点j到节点i的传播概率，Rj表示节点j的标签预测向量。

第二阶段：在标签更新时，待更新节点的邻居节点标签大部分是未知标签，若一个节点的社区类别是不确定的，那么对其邻居节点的标签影响说服力较弱。因此，为了减轻未知邻居节点对待更新节点的支配程度，除邻居节点的影响外，加入附近已知标签节点对待更新节点的影响，共同完成节点的标签更新。具体策略如下：以待更新节点为起点，应用广度优先搜索方式逐层向外搜索，直到出现已知标签节点所在层次，或查询超过3层时终止搜索。搜索到已知标签集合K，在集合K中标签数量最多的社区类别c1，会在第一阶段标签更新的基础上修改Li。因为在标签迭代更新过程中，搜索到的社区类别c1对待更新节点的影响较大，为了体现这种影响力，本文将β的取值设为0.5～1。第一阶段节点标签预测向量更新如式(4)所示。

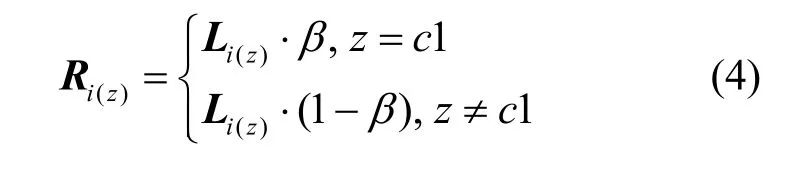
其中，Ri表示最终节点i的标签预测向量，z= 1,… ,c，Ri(z)表示节点i对第z个社区的隶属度，Li表示第一阶段节点i的标签预测向量，c表示社区类别的数量。

2.5 节点迭代传播目标函数设置

定义一个函数Yf，该函数旨在停止算法的迭代，当函数Yf的值变化很小时，节点标签趋于稳定，算法迭代停止。函数Yf如式(5)所示。

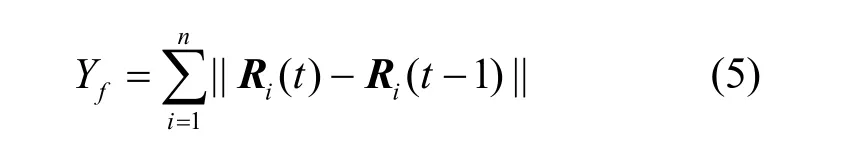
Ri(t)表示节点i当前第t次迭代的标签预测向量，Ri(t−1)表示节点i第t−1次迭代的标签预测向量，n表示节点集合V中节点的数量。

利用算法预处理阶段得到的数据，进行算法的标签传播。标签迭代传播后，每个节点被分配到对应的标签，从而确定社区检测的结果。TS-LPA的标签传播过程如算法2所示。

算法2TS-LPA的标签传播过程

输入网络G=(V,E)，最大迭代次数t_ max，图G的邻接矩阵A，节点之间影响概率值CL，网络种子集合Seed，排序后节点影响力V_Sort，节点的初始化标签向量 R_init

输出网络中最终的社区划分结果P= {P1,P2,… ,Pn}

2.6 算法复杂度分析

对于给定的网络G= (V,E)，其中V表示网络的节点集，E表示网络的边集。大小为n，大小为m，TS-LPA的时间复杂度分析如下。

计算网络中节点重要性Node(i)的时间复杂度是O(m+n)，节点重要性排序的时间复杂度为O(nlogn)，集合V的每个节点标签预测向量的初始化时间复杂度为O(n)，迭代一次的时间复杂度为O(n)，则迭代t次时间复杂度为O(nt)，有约束的广度优先搜索的时间复杂度为O( 3ndi)，其中di表示节点i的度数。综合的时间复杂度为O(m+n( 3 +t+ 3di) +nlogn)。

3 实验与分析

为了验证算法的性能，本文在真实数据集和人工数据集上分别进行了实验。实验环境是Windows10 64位版本，处理器为intel Core i5-8250U CPU @ 1.8 GHz，内存容量为8 GB，编程语言采用Python。

3.1 评价指标

标准化互信息[24]是一种衡量社区检测算法结果与真实网络在结构上是否一致的方法。通过比较社区检测的结果与标准社区结构的相似度，从而衡量社区检测的质量，对于已知社区结构的社区检测，可以衡量算法划分社区与标准社区之间的相似度。

对于给定的网络G= (V,E)，网络G划分为kt个社区，在每个社区i中，每个节点v都被分配了标签lvp=i，则真实划分T的熵计算 如下：

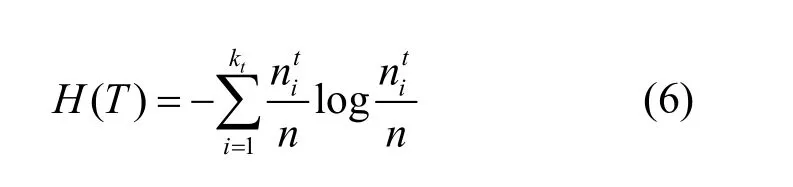
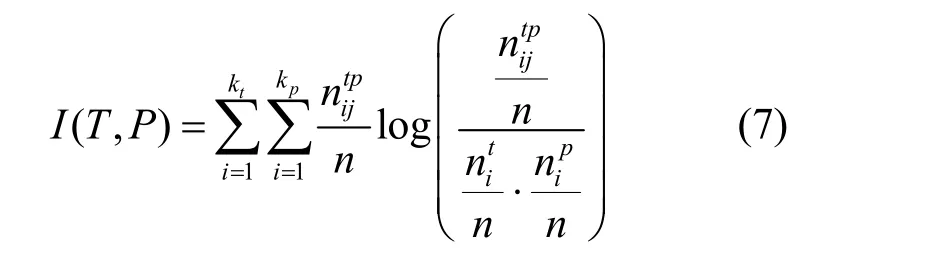
其中，kp代表预测社区检测P的社区个数，代表真实社区i和预测社区j中相同节点的个数。经过最大值(H(T) +H(P))/2正规化得到标准互信息量公式为

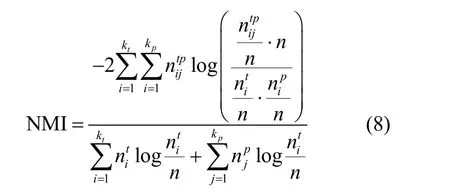
3.2 基于真实数据集实验分析

本文实验采用5种标准的真实网络数据集对数据进行社区的划分，选取的数据集分别是Karate、Dolphins、Football、Political blogs共4种公认的真实网络数据集和传销组织数据集（MLM Organization）。其参数如表1所示。

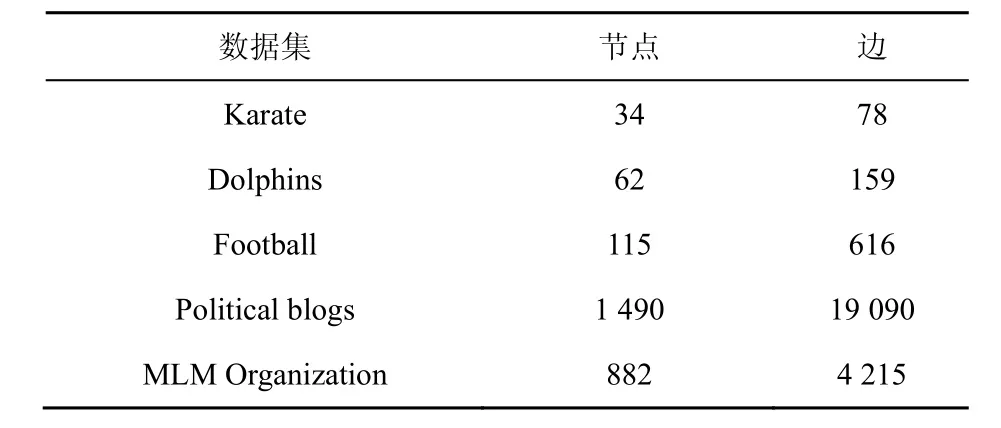
表1 真实网络数据集参数Table 1 Real network data set parameters

将TS-LPA与经典的LPA、LPAM、LPAM+、半监督社区检测算法（S_LPA[25]、KLPA[26]）进行比较，对于LPA和S_LPA两种不稳定的算法，将算法运行10次后求其平均NMI值。通过表2可以看出，TS-LPA与基于LPA的改进算法有更好的社区结构划分能力。在小规模的社区检测中，TS-LPA的算法性能与最优的算法相差不大，在涉及节点数量较多的社区检测中，TS-LPA表现出较强的社区检测能力，从而能够有效地对节点所属社区进行判断，该算法利用节点的重要性和种子节点等因素，有效提高了社区节点划分的质量，并且极大地消除了随机性，具有更好的稳定性。

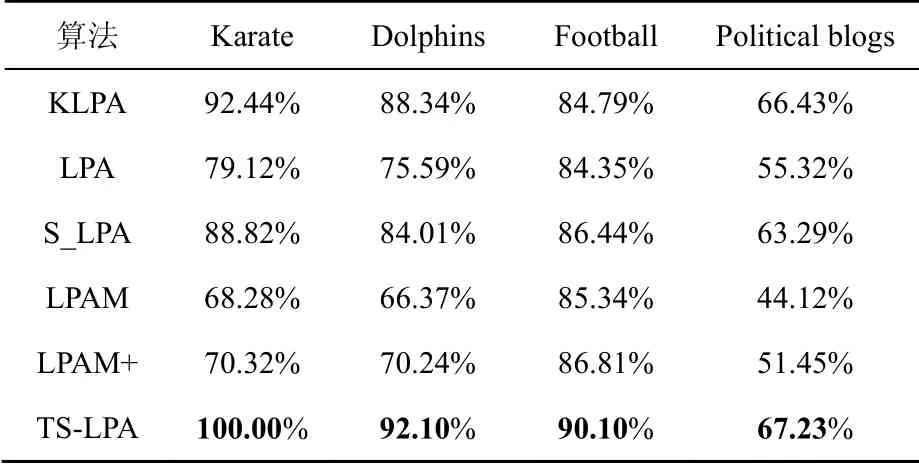
表2 真实数据集实验数据比较Table 2 Comparison of experimental data of real data sets

TS-LPA在Dolphins数据集、Football数据集，以及MLM Organization数据集上的社区划分结果如图5所示。在图5(a)中，Dolphins划分为两个社区，社区的结构相对清晰，社区成员划分与真实情况总体一致。在图5(b)中，Football数据集被划分为12个社区，蓝色的80、82、90这3个节点为已知节点，由于这3个节点所属社区属于一个管理组社区，负责对其他球队社区进行组织与管理，该社区成员与各个社区联系比较紧密，所以社区检测的识别度较小，无法形成小规模社区。但是除此之外其余社区检测结构比较清晰，根据节点的标签可以判断，实验结果各个社区的组成部分与真实情况社区的组成部分具有较高的一致性。在图5(c)中，MLM Organization数据集被划分为10个社区，由于传销组织数据网络多为自我中心网络，多数下线以头目为中心组成传销组织团伙，所以易形成网络社区。非重要传销成员之间，社区的结构比较清晰。

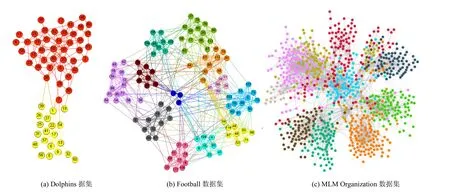
图5 TS-LPA在3个真实数据集划分结果 Figure 5 TS-LPA partition results in three real data sets

3.3 基于人工数据集实验分析

为了测试本文算法在不同网络中的适用性，本文选取人工LFR基准网络进行实验分析，并与半监督社区检测算法（S_LPA、KLPA）进行比较，选取NMI值作为社区检测准确度的评价标准，对于不稳定S_LPA，计算10次求平均值。人工合成网络分别包含1 000个节点和2 000个节点，具体参数如表3所示。其中，N代表网络中节点的数量，K代表网络的平均度值，mu代表网络混合参数，表示不同社区节点边数占网络总边数的比例，mu取值为0～1。mu值越小，人工合成的社区结构越清晰；mu值越大，人工合成的社区结构越模糊。maxk代表网络中最大度值，minc和maxc分别表示网络中社区结构的最小值和最大值。在不同mu值下，各个算法实验结果如图6和图7所示。

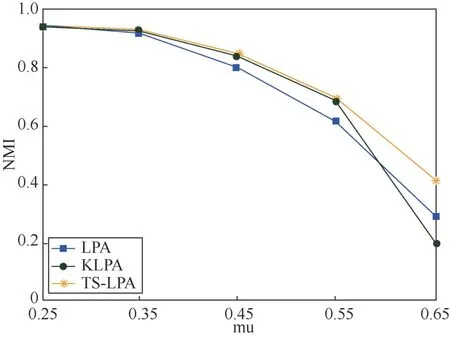
图6 当N = 1 000时不同算法数据比较 Figure 6 Comparison of data of different algorithms when N = 1 000

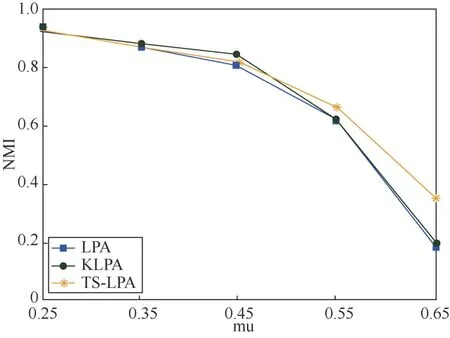
图7 当N = 2 000时不同算法数据比较 Figure 7 Comparison of data of different algorithms when N = 2 000

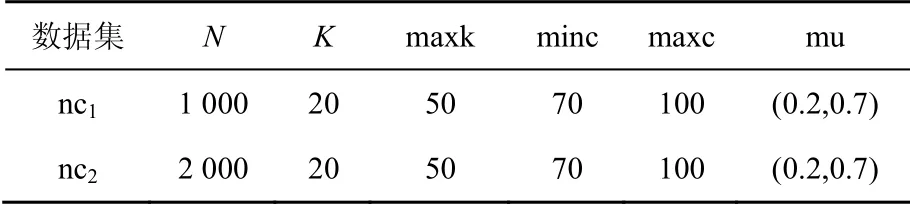
表3 人工合成网络参数Table 3 Artificial synthesis network parameters

由图6和图7可以看出，当mu<0.5时，网络社区的结构比较清晰，3种算法对社区的划分有较高的准确性。当mu>0.5时，网络社区的结构模糊，3种算法的社区检测的准确性开始下降。当N=1 000，mu>0.5时，TS-LPA对社区检测的NMI值明显优于其余两种算法，当N=2 000，mu>0.55时，TS-LPA整体高于其余两种算法的NMI值，但不明显。总体来看，TS-LPA在人工合成网络的性能优于KLPA和S_LPA。

3.4 参数的设置

TS-LPA引入参数β来确定种子节点在更新过程中标签影响能力的大小，最终影响社区结构的划分，将TS-LPA在Political blogs数据集和nc1（mu = 0.2）数据集选取不同的β参数进行实验。实验选用NMI值作为评价的标准。实验结果如图8所示，当β选取在特殊的值时，社区检测的NMI值相对较高。在不同的社交网络中，由于种子集合的选取和网络拓扑结构的不同，已知标签节点对未知标签节点的影响程度有所差异，因此，不同的网络结构需要不同的参数进行对应。

图8 不同数据集不同的β参数实验结果 Figure 8 Different β parameter detection results of different data sets

3.5 算法稳定性试验

LPA节点更新顺序的随机性和标签选择策略的随机性造成了算法的不稳定，多次运行的结果出现较大偏差。本文提出的TS-LPA在选择节点更新顺序时，通过对节点影响力进行排序来使更新顺序稳定；通过引入标签传播和广度优先的策略，确定了两阶段标签更新策略，消除了随机性。如图9所示，通过将TS-LPA在4个数据集上各进行15次运算，得到各个运行结果呈现一条直线，通过实验进行了验证。

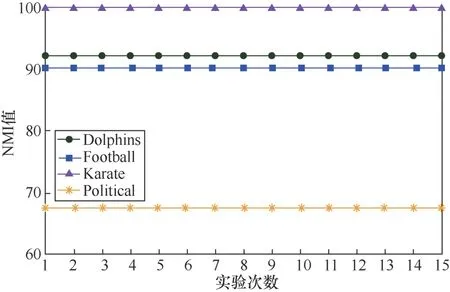
图9 TS-LPA在不同数据集多次运行结果 Figure 9 The results of multiple runs of the TS-LPA on different data sets

4 结束语

本文在标签传播算法的基础上，提出了一种基于标签传播的两阶段社区检测算法，该算法综合考虑节点的局部影响力和全局影响力来计算节点在网络中的综合影响力，使节点影响力的量化更加具体。此外，所提算法引入节点影响力信息和边的权重信息来计算节点之间的影响概率，使其更接近真实网络。在传播迭代过程中，通过未知节点邻域内已知节点的信息，实现对网络中节点的社区检测，实现标签传播过程中标签的两阶段调整，提高社区检测的准确度。实验结果证明，TS-LPA能够有效提高社区检测的准确性和稳定性。

在接下来的工作中，将进一步考虑引入方向等信息和融合其他经典的算法来实现社区检测，提高社区检测的稳定性；对算法进行优化，减小算法运行的时间和空间复杂度。