电子天平校准和测量能力(CMC)中不确定度的评定与表示
2022-04-18韩玉华
陈 露,王 琦,韩玉华,王 昱
(湖北省计量测试技术研究院,湖北 武汉 430071)
0 引言
2020年7月2日,国家市场监督管理总局发布了JJF 1847-2020《电子天平校准规范》[1],2021年1月7日起正式实施.电子天平校准规范是以国际建议(R76:非自动衡器)[2]和欧盟版电子天平校准规范(I-C-G-018)[3]为基础编写的,该规范的发布和实施将显著提高各校准实验室对电子天平校准的服务质量.
目前,在生物制药、环境监测等有关行业,日常大量使用高精度微量电子天平(万分之一精度及以上),由于中国医药企业在面临产品出口时,要经过美国药典标准(FDA)或者欧洲药典标准(EP)的严格审查,无论是FDA还是EP,都有对药物用天平的称量过程、称量数据审查的具体要求,中国制药企业为了满足以上要求,大量需要电子天平的校准数据,在称量过程中,更关注某些称量点的校准值及不确定度已经成为一种常态.
然而,现有的计量监督体系是以“检定”为主,电子天平检定规程主要评价不同称量范围的误差是否超出最大允许误差来进行符合性判断,即判定仪器是否“合格”.即便是进行校准,各级校准实验室在做电子天平校准时均参照JJG1036-2008《电子天平检定规程》[4]进行.在执行过程中,不同实验室都制定了各自的校准方法,这难免造成方法标准不统一的情况,影响后续的评价,因此不能精准满足客户需求.
为了加强国际互认,精准服务企业,全国质量密度计量技术委员会结合实际需要,特别制定了电子天平校准规范.由此,电子天平也成为经国家市场监督管理总局批准试点的第一个规程和规范同步使用的计量器具,其中检定规程主要面向法制计量,校准规范以满足客户具体需求为主.
电子天平校准规范的出台,使得方法上得到统一,同时与欧盟校准规范衔接,有利于国际互认,更有利于我国企业充分参与国际竞争.
1 电子天平的CMC评定与表示
针对电子天平最新校准规范的出台,各校准实验室势必要对电子天平的校准和测量能力(CMC)进行调整,如方法变更或重新进行不确定度评定.CNAS中校准和测量能力(CMC)是表征各实验室测量能力的指标,经过多年的普及推广,CMC已经成为衡量各校准实验室检测活动可信性、可比性和可接受性的重要参数[5].笔者在参与诸多的实验室CNAS评审过程中发现,很多计量技术人员对不同设备CMC不确定度的表示方法各不相同.有的不能完全涵盖其测量范围,有的则最优不确定度不能真实反映其校准实验室的测量能力,降低了校准实验室对外宣称的CMC的真实性和可信度[6].
表1 所示为针对电子天平的校准和测量能力表示的2个实验室的2种表达方式.可以看出,2个实验室对电子天平CMC不确定度评定和表示方法有明显的不同.两个实验室都采用了范围表示方法,但在测量范围的具体表述上存在明显的区别,方法2在测量范围的基础上还使用检定分度值e进行了限定,方法1的表示中测量范围没有进行衔接,1 kg~2 kg之间出现了遗漏,这显然不能体现该实验室的校准能力.

表1 电子天平CMC表达方法实例
由于电子天平本身是具有不同精度、不同测量范围的测量仪器,因此对某单一称量点进行不确定度评定必须要考虑其实际分度值,否则不确定度评定结果必然千差万别.以5 g这一称量点来说,从千万分之一精度(d=0.1 μg)电子天平到万分之一精度(d=0.1 mg),再到最常见的十分位(d=0.1 g)电子天平均可以覆盖该测量点,不同精度电子天平在校准过程中所使用的标准砝码、测量环境、测量程序及人员均不相同,因此其不确定度相差很大.
CNAS-CL01-G003《测量不确定度的要求》[7]中提到:“CMC是校准实验室在常规条件下能够提供给客户的校准和测量的能力.其扩展不确定度应是在常规条件下的校准中可获得的最小的测量不确定度.”换句话说,CMC中的不确定度是实验室选择的最优校准能力,不确定度更小.
因此,评定实验室最优不确定度必然要结合该测量仪器所有精度的仪器来进行考虑.CNAS-CL01-G003《测量不确定度的要求》中提到:“‘现有的最佳仪器’通常是相关测量标准在计量溯源链中可校准的最高等级(或性能)的被校仪器,可能时,选择其中具有特殊的性能(比如稳定性)或经过长期校准的仪器,但不应选择性能等于或优于所用测量标准的仪器作为“现有的最佳仪器”来评定CMC.”以电子天平为例,若某实验室在其计量溯源链中可校准的最高等级电子天平为千万分位电子天平,则针对某一特定测量范围,选择千万分位及以下所有覆盖该测量范围的不同精度电子天平为“最佳仪器”,具体以电子天平称量范围为准,对于覆盖了某一测量点的选择精度最高的天平作为“最佳仪器”.那么,针对某一测量范围,该测量范围内“最佳仪器”是必然选择.
基于此,本文结合最新发布的电子天平校准规范,对某实验室的电子天平的CMC进行评定,综合考虑选择稳定性强、重复性好、分辨力高的电子天平作为被校仪器.
2 电子天平的测量不确定度评定
2.1 电子天平不确定度评定方案
1)测量依据:JJF 1847-2020《电子天平校准规范》
2)测量环境条件:温度(20±1)℃,湿度(40~70)%RH,温度波动≤0.5 ℃/h.
3)测量标准:用于校准的标准砝码为E1,E2,F1等级标准砝码,如表2 所示.

表2 校准用标准砝码
4)测量方法:采用标准砝码直接测量电子天平各技术参数(各载荷点)的示值,可得电子天平示值与标准砝码之差,即为电子天平的示值误差.
5)被测对象:被测对象为Ⅰ级及以下电子天平,如表3 所示.

表3 被校电子天平的分类
6)测量模型及不确定度来源分析[8]
① 测量模型
电子天平的校准模型为
E=I-mref,
(1)
I=IL+δIL+δIrep+δIecc-δI0-I0,
(2)
式中:I为天平示值;mref为试验载荷的参考质量;IL为加载砝码的示值;I0为零点示值;δI0为空载示值的化整误差;δIL为加载时的示值误差;δIrep为天平的重复性误差;δIecc为由于试验载荷重心的偏心位置引起的误差.
mref=mN+δmc+δmB+δmD[9],
(3)
式中:mN为砝码的标称质量;δmc为来自上一级标称砝码的不确定度偏差;δmB为空气浮力对砝码的影响偏差;δmD为砝码不稳定性的影响偏差.
根据测量模型,合成标准不确定度的计算公式为
(4)

合成标准不确定度为
u2(E)=u2(I)+u2(mref).
(5)
② 不确定度来源
A.示值的不确定度
a.空载示值的化整误差引起的标准不确定度u(δI0).
b.加载示值的化整误差引起的标准不确定度u(δIL).
c.重复性引起的标准不确定度u(δIrep).
d.偏载引起的标准不确定度u(δIecc).
B.参考砝码的标准不确定度
e.标准砝码的标准不确定度u(δmc).
f.空气浮力引起的标准不确定度u(δmB).
g.砝码不稳定性引起的标准不确定度u(δmD).
C.电子天平不确定度评定影响因素分析
示值误差的合成标准不确定度u(E)根据式(6)计算
u2(E)=u2(δI0)+u2(δIL)+u2(δIrep)+
u2(δIecc)+u2(δmc)+u2(δmB)+u2(δmD)=
(6)
在相同的实验环境下,控制各其它变量,均采用相同的测量方法,相同的测量模型,则根据式(6)可知,电子天平在相应载荷点的扩展不确定度主要与5个方面有关,如表4 所示.
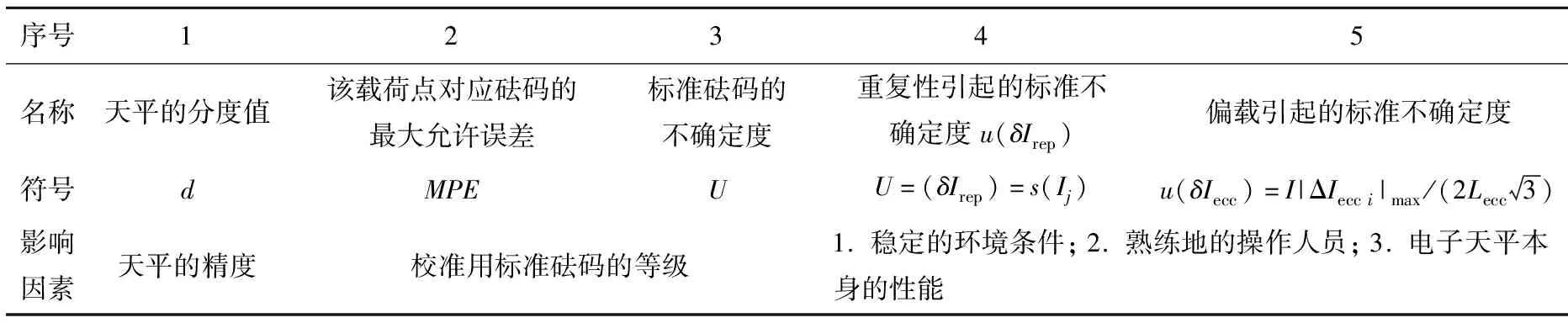
表4 电子天平不确定度影响分类
由表4 可知,想要获取更优的不确定度,要尽可能选择与其相匹配的标准砝码或更高等级砝码.这样,MPE和U取值更小.而更加稳定的环境条件,熟练的操作人员则可以使重复性引起的标准偏差更小,电子天平本身的性能则直接影响了偏载引入的不确定度.
基于此,为了获得CMC最优不确定度,结合前述不确定度影响因素的分析,严格控制环境条件,选择熟练的技术人员,按照不同等级电子天平,结合其精度,选择最适合的标准砝码,进行电子天平不确定度评定实验,最终计算出的结果即为实验室最优不确定度.
2.2 标准不确定度评定实例[10]
以METTLER TOLEDO生产的超微量天平为例,该天平型号XPR6U,准确度等级为I级,最大秤量6.1 g,分度值d=0.1 μg,所用标准砝码为E1等级砝码.
1)空载示值的化整误差引起的标准不确定度u(δI0),δI0表示空载示值的化整误差.其区间半宽度为±d0/2;服从矩形分布
0.000 029 mg.
(7)
2)示值的化整误差引起的标准不确定度u(δIL),δIL表示加载时的示值误差.其区间半宽度为±dL/2,服从矩形分布.因此
0.000 029 mg.
(8)
3)重复性引起的标准不确定度u(δIrep),δIrep表示天平的重复性误差,服从正态分布,估计为
u(δIrep)=s(Ij).
(9)
重复性采用5 g的测量点,进行10次连续测量,如表5 所示.

表5 重复性测量数据
u(δIrep)=s(Ij)=0.000 61 mg.
(10)
4)偏载引起的标准不确定度u(δIecc),δIecc表示由于试验载荷重心的偏心位置引起的误差.偏载测量数据如表6 所示.

表6 偏载测量数据
4 999.991 7 mg×0.002 3 mg/(2×2 000 mg×
(11)
示值的标准不确定度通过下式获得
u2(I)=u2(δI0)+u2(δIL)+u2(δIrep)+
u2(δIecc)=0.000 0292+0.000 0292+
0.000 612+0.001 662=0.001 772,
(12)
则
u(I)=0.001 77 mg.
(13)
5)标准砝码的标准不确定度u(δmc), 如果标准砝码校准证书中给出了砝码的约定质量以及校准不确定度U和覆盖因子k,其标准不确定度
u(δmc)=U/k.
(14)
标准砝码选择E1等级,U=0.005 mg,则
u(δmc)=U/k=0.005 mg/2=0.002 5 mg.
6)空气浮力引起的标准不确定度u(δmB).
因在校准之前已对天平进行调整,因此
0.002 3 mg.
(15)
7)砝码不稳定性引起的标准不确定度u(δmD).
D的值将根据JJG 99选择最大允许误差的1/3,在±D范围内服从正态分布.因此
0.000 96 mg.
(16)
参考质量的标准不确定度通过下式获得
u2(mref)=u2(δmc)+u2(δmB)+
u2(δmD)=0.002 52+0.002 32+
0.000 962=0.003 52,
(17)
则
u(mref)=0.003 5 mg.
(18)
示值误差的合成标准不确定度u(E)根据下式计算
u2(E)=u2(δI0)+u2(δIL)+u2(δIrep)+
u2(δIecc)+u2(δmc)+u2(δmB)+u2(δmD)=
0.001 772+0.003 52,
(19)
则
u(E)=0.003 9 mg.
(20)
因重复性次数为10次,
(21)
根据向下舍入原则,选择有效自由度为50,查表得覆盖因子k=2.05,为保证后续扩展不确定度的表示统一,按95%的置信区间,统一取k=2,则示值误差的扩展不确定度U=2u(E)=0.007 8 mg.
根据上述的方法,对校准范围内的其它3个代表性载荷点的不确定度进行评定, 如表7 所示.

表7 不确定度的计算汇总表
2.3 不同精度电子天平不确定度评定结果
采用与前述相同的方法对其它精度电子天平进行校准,则各精度电子天平的扩展不确定度如表8 所示.
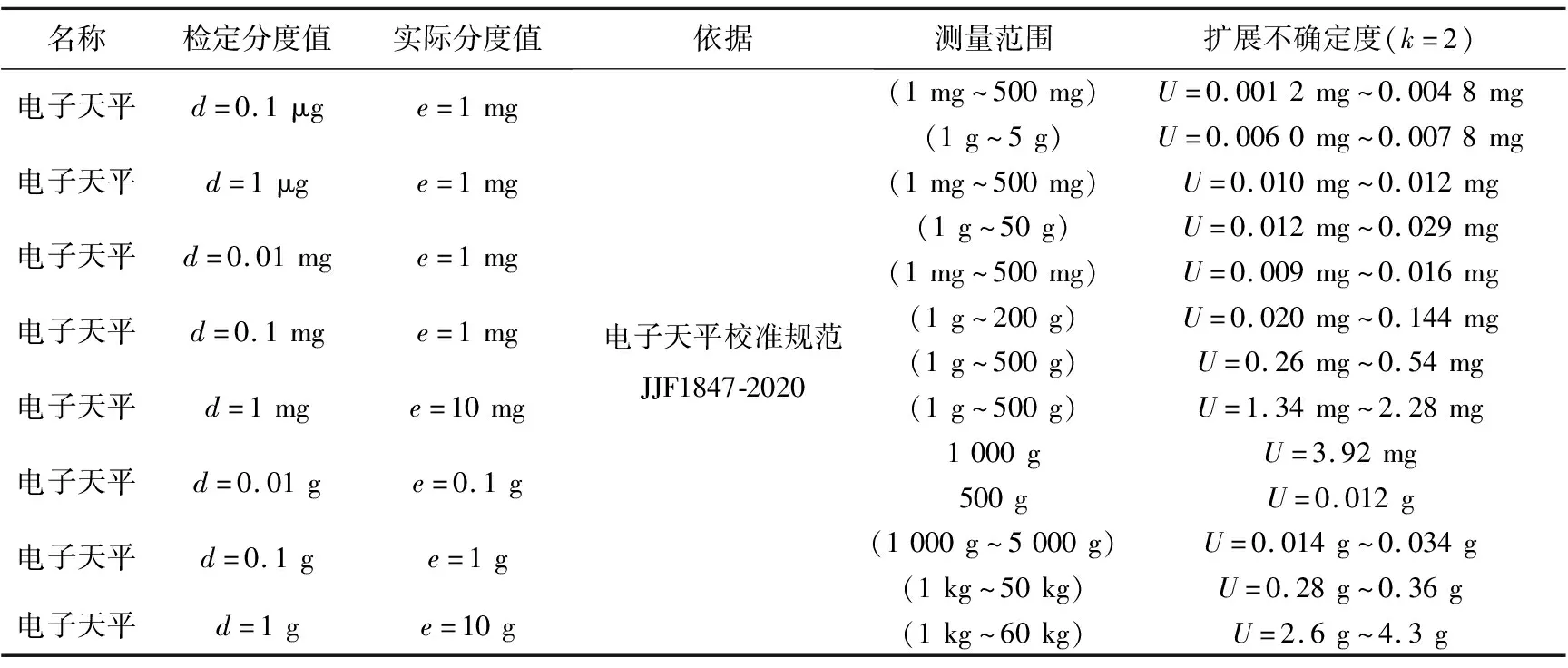
表8 不同精度电子天平的扩展不确定度汇总
3 电子天平校准和测量能力表示
表8 中归纳了该实验室不同精度电子天平的不同测量范围的扩展不确定度.前述提到,对某实验室的电子天平的CMC进行评定,综合考虑选择稳定性强、重复性好、分辨力高的电子天平作为被校仪器.那么,对某一特定测量范围,应选择该测量范围不确定度更小的值作为该实验室电子天平的CMC.
举例来说,对于测量范围1 mg~500 mg,由于所有精度电子天平均可覆盖,那么在选择最优校准能力时,取其所对应测量点(端点)不确定度更小的即可.1 mg对应不确定度最小的值为 0.001 2 mg(千万分位电子天平,精度:d=0.1 μg).同理,500 mg测量点不确定度U=0.004 8 mg.由此可知,测量范围1 mg~500 mg,其最优校准能力为U=0.001 2 mg~0.004 8 mg.同理,根据表8 中不同精度电子天平的扩展不确定度,对不同测量范围,选择其测量范围两端载荷点的最优不确定度作为CMC中扩展不确定度的极值(加粗部分为极值点),则该实验室申请认可的能力范围如表9 所示.

表9 电子天平CMC表示
可以看出,该实验室电子天平的校准和测量能力(CMC)既涵盖了其所能覆盖的测量范围,又真实反映了其校准实验室的最佳测量能力,概括精炼,完全符合CNAS-CL01-G003《测量不确定度的要求》.当然,为了日常使用方便,某些实验室以电子天平精度进行划分,在测量范围的基础上还使用检定分度值e进行了限定,这种CMC表示方式也是可取的,只不过操作起来更加复杂.
4 结束语
本文结合电子天平校准规范的出台,对某实验室的电子天平校准和测量能力进行了重新评定,有效提高了相关人员的能力.为确保评估的CMC反映真实的校准水平,实验室应充分考虑对校准结果不确定度的影响因素.针对电子天平而言,保持稳定的实验室环境、选择有经验的操作人员、使用更高等级的测量设备、关注测量设备的溯源性等,是保证实验室更优校准能力的前提.
需要指出的是,截至2020年11月,我国累计认可的各类合格评定机构有12 192家,认可现行有效认证证书140多万张[11].在生物安全、医学检疫、医药卫生、国防等诸多领域对各类实验室进行了评审认证.笔者结合日常在监督评审过程中发现的一些关于“测量设备校准和测量能力评定与表示”的常见性问题,以电子天平这一代表性测量设备为例,对电子天平校准和测量能力(CMC)中不确定度的评定与表示进行研究,希望给相关实验室技术人员一个指引,规范评定工作,提升各实验室检测能力的公信力.
