优先级评估下的软件源文件可疑度度量方法
2022-04-18朱镕申孙川钘
朱镕申,孙川钘,黎 秀
(电子科技大学成都学院,四川 成都 611731)
1 引言
软件产业的不断进步,让计算机领域对软件质量的需求日渐提升,但也不断出现软件源文件代码缺陷问题,大幅度提升系统事故概率。软件源文件缺陷表示源代码内包含语法、拼写或标点错误[1],这样会严重影响用户的实际操作应用。想要提升软件质量,一定要有效管理与修复源文件代码缺陷,对其采取可疑度度量,从而明确产品是否存在缺陷,保证软件产品的正常使用[2,3]。
关于软件缺陷检测问题,文献[4]利用耦合重启随机游走与标签传播方法,从软件调用关联、模块风险度与历史缺陷报告来探究缺陷方位,把缺陷定位划分成风险度与标签两种传播模式,明确软件缺陷情况。文献[5]通过获取程序函数调用序列,比较待测目标序列与可疑序列,去除已检测函数,获得缺陷函数候选集,实现缺陷函数定位。
但上述两个方法均没有计算缺陷之间的属性值,无法完全保障缺陷位置定位准确性。因此本文提出一种优先级评估下的软件源文件可疑度度量方法。运用优先级评估策略完成源文件可疑度度量大小排序,推算缺陷数据与源文件之间的关联性,使用基于支持向量回归的软件源文件易错性方法,获得软件源文件相对的缺陷密度,从而获得软件源文件可疑度,明确源文件产生缺陷的概率。
2 基于优先级评估的软件源文件可疑度度量方法
在优先级评估基础上融合软件源文件缺陷定位有关内容与缺陷预测手段,设计一种基于优先级评估的软件源文件可疑度度量方法。可疑度越大,证明源文件产生缺陷的几率越高。创建源文件可疑度度量方法整体架构,具体参见图1。
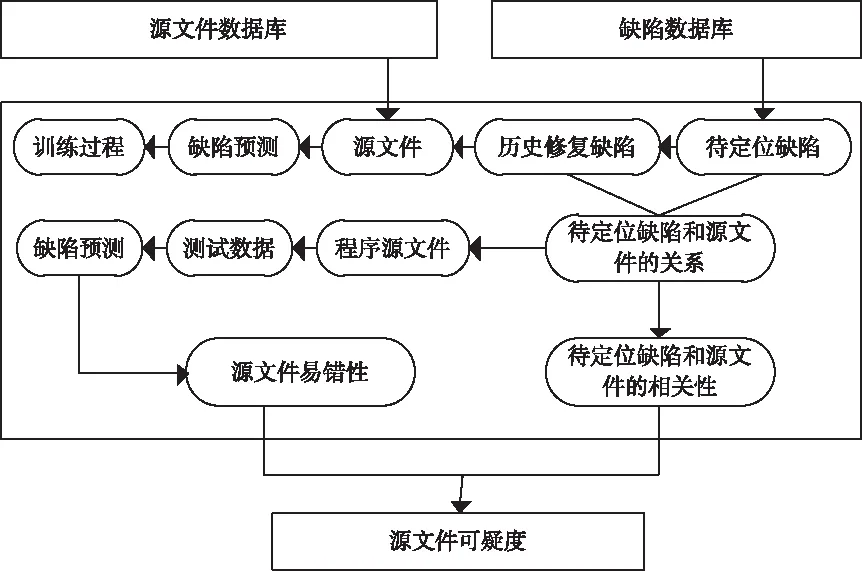
图1 软件源文件可疑度度量过程
将可疑度计算解析式描述为
Score=(1-a)Score1+aScore2
(1)
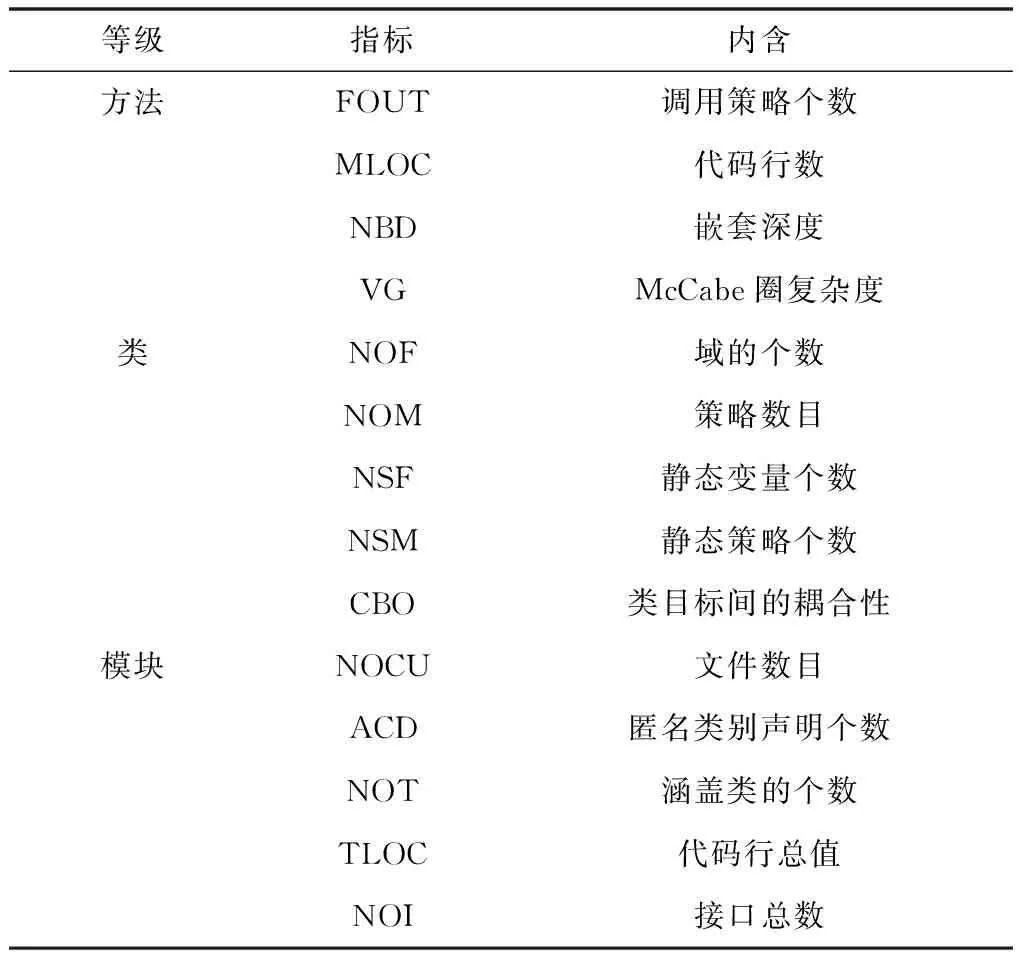
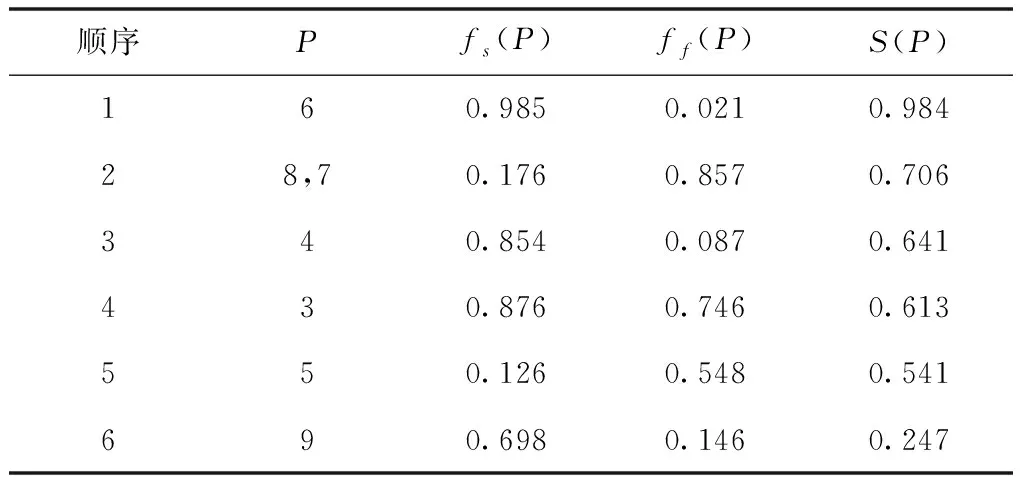
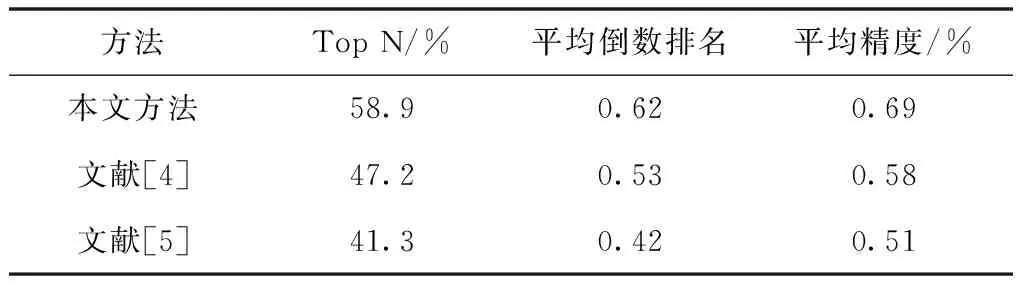
式中,Score1代表源文件和待检测缺陷的关联度,Score2是源文件易错水平,参变量a用于调节关联度与易错水平处于可疑度度量过程中的权重,保证0 在计算可疑度之前,首先对其进行定量分析,在可疑度优先级排列的多属性决策中,决策群体为E={e1,e2,…,en},使用ω描述专家权重。优先级评估排序需求集合是R={r1,r2,…,rk},可疑度需求评估属性是F,评估属性权重是λ。 度量决策者es对度量需求ri属性的打分过程为 (2) (3) 决策群体对度量需求评估的结果通过个体决策与专家权重计算得到,记作 (4) 软件源文件缺陷通过诸多特征属性表示,划分成标称与序数两个类别,如表1内的缺陷数据,表内缺陷类别1与2为标称属性,3为序数属性。 表1 软件源文件缺陷数据表 按照数据挖掘有关定理,数据间的相邻性包含相似与相异两种性质。在目标i、j的标称属性匹配情况下,相似性sim(i,j)=1,相异性d(i,j)=0。 标称属性一般使用布尔度量方法,如果两个目标互相匹配,相似性等于1,反之等于0。序数属性与标称数据的区别在于:具备抽象意义的序数属性值可使用距离来推算源文件缺陷相似度[8],计算过程为:首先设置第i个目标的序数属性f的值是rif,属性f内含有Mf个有序状态。其次,因为每个序数属性极有可能产生差别较多的状态数,为了让属性间的相异性处于(0,1)取值范围内,要规范化属性值,得到 (5) 再把缺陷序数属性实施距离计算,针对单属性来说,使用欧几里得距离[9]描述两个缺陷样本间的相异性大小 (6) 融合粗糙集理论与模糊聚类算法解析软件缺陷数据,划分缺陷属性权值,详细过程如下: 第一,构建缺陷数据编码表,抽象化处理数据,每个缺陷均是通过n个抽象化特征值定义的矢量,将全部缺陷数据当作特征空间内的多维矩阵,表示成 (7) 第二,组建模糊相似矩阵T,推导过程为 (8) 式中,n表示矩阵列数。 第三,分割不同的临界值面积来阐明缺陷数据间的相似性,按照模糊等价矩阵内的缺陷数据相似性,分别把缺陷数据划分成各不相等的类型。 第四,利用粗糙集内关键性定理算出属性权重值。将缺陷数据划分结果D的特征属性C依赖度描述成 γ(C,D)=|POS(C,D)|/|U| (9) 其中,|POS(C,D)|代表正域的缺陷数量,|U|代表缺陷数据非空集合内的缺陷数目。 将属性的关键性记作 SGF(f,C,D)=γ(C,D)-γ(C-{f},D) (10) 则属性全局关键性为 (11) 根据属性的关键性排名,推算每个属性自身的权重值 (12) 由此将缺陷数据与软件源文件的相关性推导公式记作 (13) 式中,Similarity(B,Si)是缺陷数据与过往修正缺陷的相似性,m是全部和源文件相关的缺陷个数。 为了保证软件源文件可疑度度量的正确性,首先要明确软件缺陷的度量元。以往缺陷定义均采用代码行当作度量准则[10],而后又相继研发出一系列面向目标的软件研发技术,得到软件度量元,例如内聚性、耦合性等。本文方法的度量元如表2所示。 表2 软件源文件缺陷定位度量元 易错性即为源文件缺陷密度大小,密度越大,易错性越强,可疑度越高。代入Spearman秩相关数算法,衡量度量元和源文件缺陷密度间的关联,得到对缺陷密度影响最高的度量元,并剔除多余度量元。假设软件源文件的度量元为H,缺陷密度为I,把H、I内的数据实施匹配,获得数据集合(H1,i1),…,(Hk,ik),把Hk、ik依次根据大小排列,得到二者在第二个次序样本内的排名,定义成Rk、Sk。则H、I之间的关联水准计算公式为 (14) 为防止数据处理时由于某些度量元数值差异较多影响运算正确率,需要预处理数据。归一化是把度量元属性值整合至[0,1]区间。归一化单个维度下的度量元数据,得到 (15) 使用支持向量回归完成源文件代码易错性预测。设定一个数据集{(h1,i1),…,(hl,il)},hl是第l个软件源文件的度量元矢量,il是第l个源文件缺陷密度。使用Rn内的函数f(x)进行数据拟合,函数的表达式为 f(x)=w·x+b (16) 其中,w代表超平面的法矢量,b是一个任意常数。 可疑度度量的计算过程就是探寻一个最佳超平面,让全部样本点与超平面的偏差总值距离为最短,使用具备正则化特征的偏差函数进行距离运算,得到 (17) 其中,f(xe)是第e个软件项目缺陷密度评估值。 将软件源文件易错性问题变换成最优问题,得到 (18) (19) 代入一个拉格朗日乘子α,获得如下对偶表达式: (20) 其中,K(xi,xj)是一个核函数。 最终得到支持向量回归下的易错性预测模型是 (21) 利用式(21)即可在输入任意度量元矢量的情况下,得到软件源文件相对的缺陷密度,完成易错性计算全过程。 挑选模型内的核函数,恰当的核函数可把低维空间非线性问题变换成高维空间线性问题,探寻回归问题的最佳超平面。运用径向基核函数优化预测模型,将优化过程描述成 (22) 其中,xj表示径向基核函数中心位置,σ是径向基核函数的宽度指数,与核函数径向作用区域面积有直接关系。 模型参变量优化的根本含义是面向各类性质不同的目标择取恰当的(C,g)数据对。在缺陷密度预测模型内设定C、g的取值范围,按照搜寻步长把C、g依次分割成n1、n2个集合,再匹配合适的数值,组成n1·n2个(C,g)数据对。利用网格搜寻实现参变量遍历搜寻,并将预测准确率最大的(C,g)数据当作最优参数,实现易错性预测评估,并综合缺陷数据与源文件的关联性计算结果,二者相加实现高精度软件源文件可疑度度量。 利用仿真证明所提方法的性能优越,所使用的仿真环境为2GHzCPU、内存2G的计算机,实验平台为Matlab 7.1。创建两个不同的待测程序,各个程序内均涵盖一个缺陷。将软件源文件中的代码作为实验对象,计算其可疑度大小,利用本文算法思想,以源文件谓词代码为例,将其可疑度计算过程描述为 Φ(P)=nt(P)/(nt(P)+nf(P)) S(P)=-lg(sim(fs(P),ff(P))) (23) 式中,nt(P)是谓词代码,P是无缺陷的次数,nf(P)是有缺陷次数,S(P)是可疑度,sim(fs(P),ff(P))是随机相似度函数。 将本文方法下的两个待测程序谓词代码可疑度度量结果表示成表3与表4。 表3 待测程序1的可疑度列表 表4 待测程序2的可疑度列表 在表3与表4中,可疑度S(P)是fs(P)和ff(P)二者间的差异,S(P)值越趋近1,证明软件源文件谓词代码P具备缺陷的概率越高,即可疑度越大,反之概率越低,可疑度越小。 通过实验结果看出,包含缺陷的第6个与第15个谓词代码可疑度为最高,排在可疑度表格的首位,且可疑度从大到小排序,逐步趋近于0。在两个表格内,第8个与第7个的谓词代码可疑度相同,表明两个分支在源文件内具备同时执行与不执行的耦合关联,则依照实验结果,缺陷检测人员首先要勘测可能包含缺陷的分支语句,缺陷极有可能隐藏在分支语句中,实现了预期可疑度度量目标。 为进一步验证本文方法的可靠性,将软件数据集SWT3.1作为实验对象,和文献[4]、文献[5]进行可疑度度量分析,表明本文方法对提升软件源文件缺陷定位的实用性。实验中使用三类指标用于衡量可疑度度量缺陷定位方法的性能,TopN表示返回结果内缺陷文件的定位个数,平均倒数排名是对全部的排序进行统计分析的过程,排名值越大,表明方法计算正确率越好。平均精度是对全部排序表的全局评估。将三种方法的缺陷定位结果表示成表5。 表5 SWT3.1数据集缺陷定位结果对比 从表5可知,本文方法三种指标的值均为最高的,证明该方法较比文献方法,在源文件可疑度度量方面占据更大的优势。这是因为本文方法采用优先级评估算法,运用评估结果明确软件源文件可疑度大小,让软件研发者有更充裕的时间完成缺陷修复,让软件安全平稳运行。 面向软件源文件代码缺陷问题,提出一种优先级评估下的软件源文件可疑度度量方法。所提方法使用优先级评估手段排列软件源文件缺陷可疑度大小,并快速计算出缺陷数据与源文件的关联性,运用支持向量回归方法创建易错性预测模型,完成高质量软件源文件缺陷定位目标。在下一步工作中,会简化权重计算方法,增强方法计算效率。2.1 基于优先级评估的问题描述
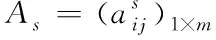
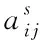

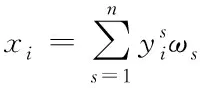
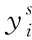
2.2 缺陷数据与源文件的关联性计算





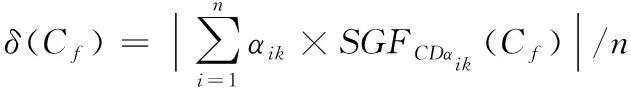

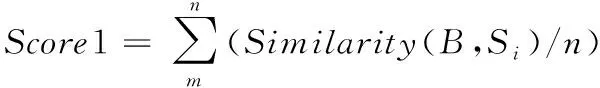
2.3 支持向量回归下的源文件易错性计算

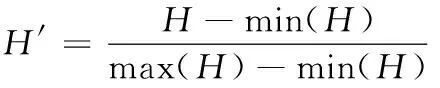
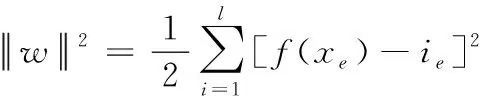

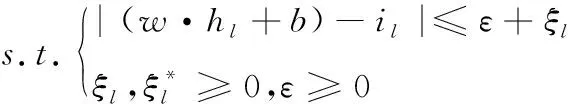
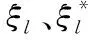
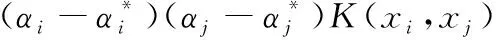
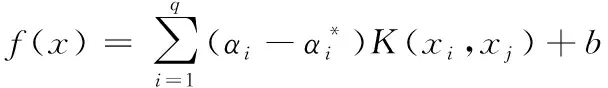
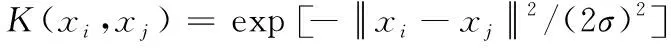
3 仿真研究

4 结论
