一种新的sin-BOC(kn，n)信号边峰消除方法

孙希延，刘泽伟，纪元法，郭 宁

(1. 桂林电子科技大学广西精密导航技术与应用重点实验室，广西 桂林 541004；2. 桂林电子科技大学卫星导航与位置服务国家与地方联合工程研究中心，广西 桂林 541004)

1 引言

近年来，GNSS在民用领域得到了更加广泛的应用。在GNSS现代化的过程中，创造性的提出了BOC调制方式。作为一种新型导航信号，与传统的二进制相移键控(Binary phase shift keying，BPSK)调制相比，BOC调制在载波调制之前加入了方波子载波调制。这使得经扩频调制后的基带信号的频谱被重新得到一次调整，从而具有优秀的频谱分裂特性。这种特性将使导航信号能够更加有效的利用有限的频带资源。但是，扩频码的二次调制使得BOC信号相关函数表现出多峰特性。并且随着调制阶数的增加，自相关函数的边峰数量随之增加。这将导致卫星信号在接收过程中捕获锁定到错误的码相位，从而带来严重的跟踪歧义。因此，消除BOC相关函数的边峰问题，成为解决BOC信号定位精度的重要环节。

目前，为了消除BOC调制信号多峰特性所带来的模糊度问题，学者们提出了三种主流的研究思路。一种是根据信号特性，通过类比传统调制进行信号简化，如BPSK-like法。这种方法利用BOC信号频谱分裂特性，可将其看做多个BPSK信号的叠加，进而通过重构得到相关峰为一个单峰的检测量。该方法具有很强的通用性，但是无法保留BOC信号窄相关峰特性，也失去了定位精度高的优势。另一种是通过增加相关器和环路复杂度实现码相位的正确捕获，如峰跳(Bump-jump)法。这种方式在传统的跟踪环路中增加了超超前和超滞后支路，进而构成主鉴别器和子鉴别器。通过判定两个鉴别器输出判定是否锁定在正确的跟踪点。该方法具有很高的跟踪精度，但是表现出较长的锁定时延，不能完成较高的实时性要求。第三种是构建一些特殊的本地码与接收信号之间的辅助相关函数，利用辅助函数本身或与自相关函数之间的非线性组合生成无副峰的相关函数，如SCPC法和ASPeCT法。SCPC法采用BOC和QBOC的互相关函数与BOC自相关函数的平方和，以达到生成没有过零点的相关峰的目的。该方法运算简单，但该相关峰的跨度过大，丧失了BOC信号的捕获精度。ASPeCT法采用BOC信号自相关函数的平方减去β倍的其与PRN序列互相关函数的平方，生成消除边锋相消的相关函数。该方法复杂度较低，有效抑制了相同码相位处的边峰，但不能完全消除BOC信号副峰，且只针对sin-BOC(n，n)信号。

本文提出一种新的适用于sin-BOC(kn，n)的边峰消除方法。该方法通过将本地BOC(kn，n)信号在一个副载波周期内拆分为2k个支路信号。支路信号与接收信号进行相关运算，生成2k个辅助相关函数。构建非线性组合规则，利用辅助相关函数生成完全消除边峰的相关函数。不同于传统的构建辅助相关函数方法，本文提出的方法在保证消除BOC信号边峰的同时，能够简化环路复杂度。实验结果表明，本文提出的方法在边锋消除有效性、检测概率、峰均比、鉴相曲线、抗多径性能等方面均有不同程度的提升。

2 BOC(kn，n)信号及多峰特性

BOC调制信号通常记为BOC(m，n)的形式，表示副载波频率为基准频率f0=1.023MHz的m倍，伪随机噪声(Pseudo random noise，PRN)码速率为基准频率的n倍。在实际应用中，通常有m≥n。N=2m/n为BOC信号的调制阶数。对于BOC(kn，n)信号，调制阶数为N=2kn/n=2k。

BOC调制信号实际上可以表示为BPSK调制信号与一个方波子载波的乘积形式，具体的时域表达式为

s(t)=sBPSK×sign(sin(2πfχt+ψ))

(1)

其中，sign(·)表示信号函数，fχ表示子载波频率，ψ表示子载波初始码相位。通常情况下，ψ可取0°或90°，分别代表sin-BOC和cos-BOC调制。BPSK调制信号具体可写为

×cos(2π(fIF+fd)t+θ)

(2)

其中，Ps为信号功率，D(t)为卫星导航数据，sc(t)为伪码信号，fIF为中频，fd为多普勒频率，θ为初始码相位。

在BOC信号体制中，相同调制阶数的信号的频谱、功率谱、自相关函数等特征一致。为了便于研究，本文将借助BD B1C采用的BOC(1，1)所代表的BOC(n，n)信号和GPS L1M采用的BOC(10，5)所代表的BOC(2n，n)信号为例，设定副载波相位为0°，sin-BOC信号自相关函数如图1所示。

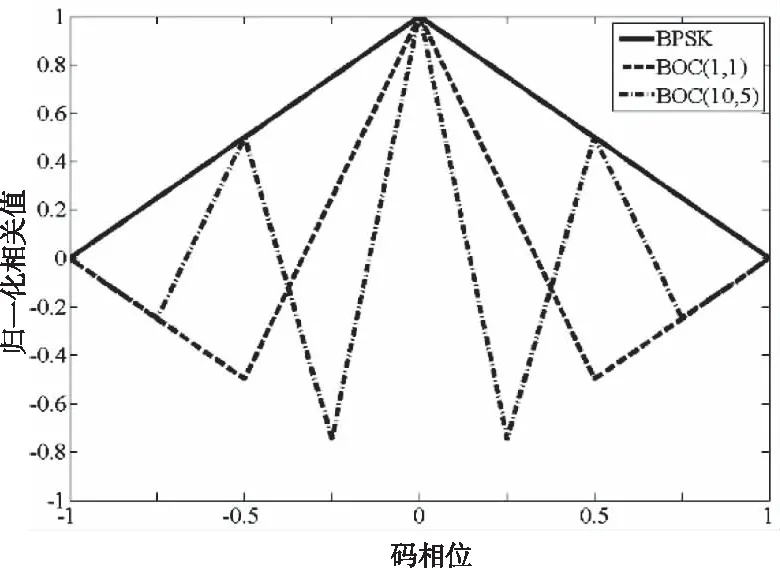
图1 BOC(kn，n)的自相关函数

如图1所示，BPSK调制的传统导航信号的自相关函数只有一个相关峰，该相关峰跨度大，捕获精度较低。BOC(1，1)调制信号自相关函数有2个边峰，BOC(10，5)调制信号自相关函数有6个边峰。有效消除BOC调制的边峰影响，能更好提高接收机的稳定性。

3 sin-BOC(kn，n)边峰消除算法

在忽略多径和噪声干扰的条件下，可以设定本地BOC信号为

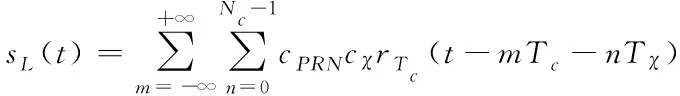
(3)

其中，cPRN为伪码符号，cχ为副载波脉冲电平值，Nc是单个伪码码片多对应的脉冲个数，Tc是伪码码片宽度，Tχ是副载波脉冲持续时间。对于BOC(kn，n)信号，有Tχ=Tc/2k。

以一个伪码宽度的1/2k长度为基准，利用时域控制器，将本地BOC信号拆分为2k段。此时，i支路BOC信号可以表示为

(4)

根据信号分解定义，能够得出结论如下

(5)

分别以BOC(n，n)和BOC(2n，n)信号为例，具体拆分过程如图2和图3所示。

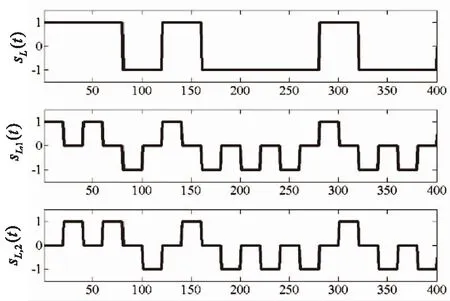
图2 BOC(n，n)分解信号

图3 BOC(2n，n)分解信号

将经过分解后提取的支路BOC信号与接收信号相关后，产生子相关信号。具体表达式为

(6)

其中，Ri(τ)表示i支路BOC信号与接收信号子相关函数，Tcoh为非相干积分时间。根据分解定义，能够得出结论如下

(7)

分别以BOC(n，n)和BOC(2n，n)信号为例，生成子相关函数的具体过程如图4和图5所示。

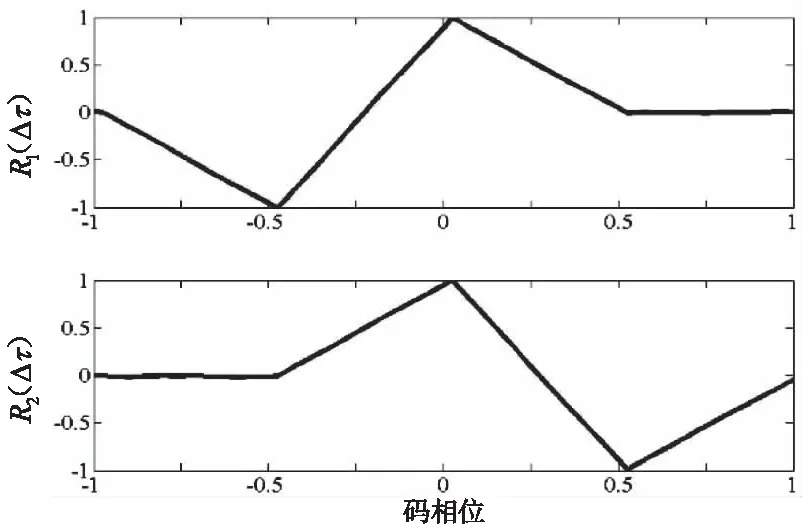
图4 BOC(n，n)相关函数分解过程

图5 BOC(2n，n)相关函数分解过程

通过分析BOC(kn，n)信号分解过后生成的辅助子相关函数，可以发现，将2k个辅助相关函数之间呈现平移翻转关系。利用第1子相关函数与第2k子相关函数做模加和相减运算。能够得到边峰消除的相关函数。该过程的具体表达式如下

(8)

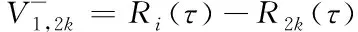
(9)

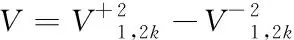
(10)

根据上述原理，能够得到对BOC(kn，n)的无模糊度相关函数生成过程如图6和图7所示。

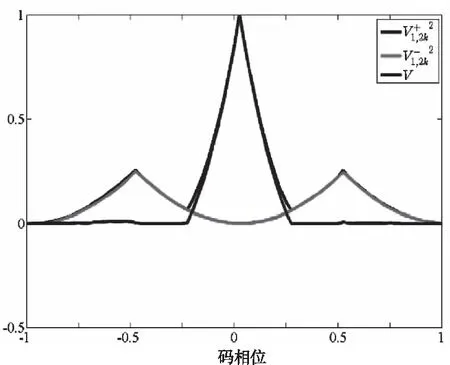
图6 BOC(n，n)边峰消除相关函数生成过程

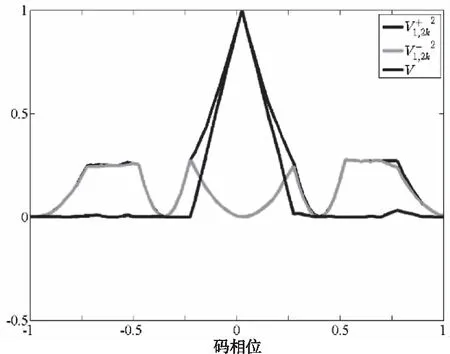
图7 BOC(2n，n)边峰消除相关函数生成过程

本文提出新的边峰消除相关函数本质上是利用新生成的辅助信号产生新的边峰消除相关函数。因此，本文方法的具体实现流程结构框图如图8所示。

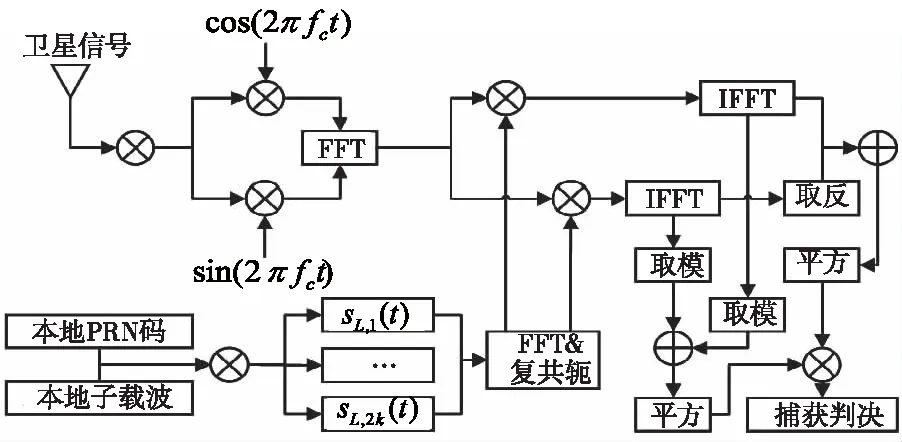
图8 本文方法流程框图

在跟踪过程中，接收信号与本地I、Q相位载波相关分离，再经过滤波操作。接着，两路信号经超前滞后处理，与本地码相关。通过积分清除滤波器，得到相关函数可以表示为

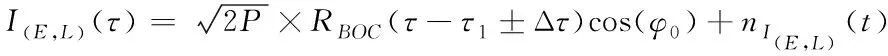
(11)

(12)

其中，I(E，L)(τ)、Q(E，L)(τ)表示I、Q支路超前滞后相关函数。nI(E，L)(t)、nQ(E，L)(t)表示服从高斯分布的噪声。

通过参考文献中，我们可以查询到鉴相器函数的表达式可以写作：

DF(τ)=RE(τ)-RL(τ)

(13)

根据最终边峰消除相关函数的生成规则，可以得出本文方法的鉴相器函数表示为：

DFpro(τ)=((|IE|+|QE|)2-(IE-QE)2)

-((|IL|+|QL|)2-(IL-QL)2)

(14)

4 实验与对比分析

为了充分展现本文所提出的边峰消除方法的性能及通用性，综合考量本文方法的应用范围。本节将采用BOC(n，n)信号与BOC(2n，n)为实验分析对象。从下列几个维度，对比本文方法和其他方法之间的性能差异。

4.1 边峰消除有效性分析

设定采样频率为fs=16.368MHz，中频频率为fIF=10MHz，多普勒频移为fd=3KHz，多普勒搜索范围为[-10kHz， 10kHz]、多普勒搜索步长为500Hz、信噪比为0dB。为了便于分析各种算法间的去模糊度有效性，分别对各方法得到的最终相关函数做归一化处理。图9和图10分别表示对BOC(n，n)和BOC(2n，n)信号的边峰消除结果。结果表明，本文提出的方法能够完全消除sin-BOC(n，n)和sin-BOC(2n，n)信号边峰，在方法对比中边峰消除有效性最好。

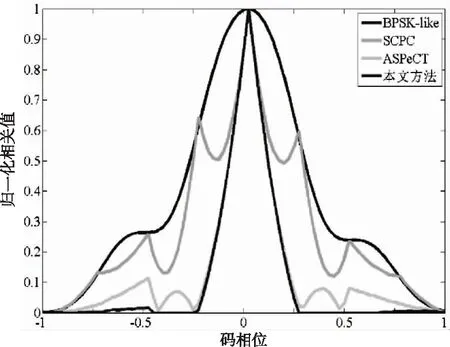
图9 BOC(n，n)边峰消除有效性对比

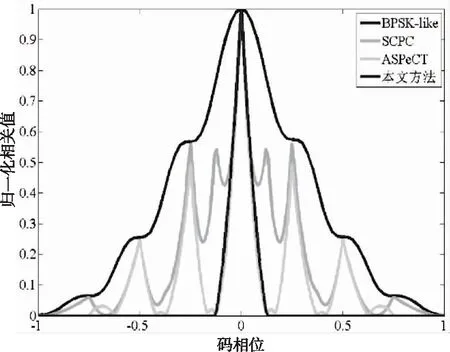
图10 BOC(2n，n)边峰消除有效性对比

4.2 鉴相函数曲线分析

为了评估各方法的跟踪性能，对各方法的鉴相函数曲线结果进行分析。设置相关器相关间隔为0.05码片，前后向滤波器带宽为无限大。在不同调制阶数下的鉴相输出结果如图11和图12所示。本文方法去除了误锁点，在零点附近的斜率也保持在较高水平。

图11 BOC(n，n)鉴相曲线对比

图12 BOC(2n，n)鉴相曲线对比

4.3 检测概率分析

与BOC信号的跟踪过程相比，BOC信号的捕获是检测统计量与检测阈值之间的比较。在该小节中，采用蒙特卡罗方法将最终边峰消除相关函数所表示的码相位与实验设定的阈值进行比较，判断是否正确捕获信号。

设定信噪比范围为[-40，-20]，最终检测函数与真实信号的码相位误差门限为[-5，+5]。统计四种不同方法在不同信噪比情况下重复20000次捕获实验的检测结果，计算检测概率。实验结果如图13和图14所示。选定信噪比-26dB时的检测概率作为比较对象，对于BOC(n，n)信号，能够看出本文方法较BPSK-like、SCPC和ASPeCT方法提升明显。而对于BOC(2n，n)信号，本文方法的检测概率仍有一定差距。这也是本文方法存在的问题之一。

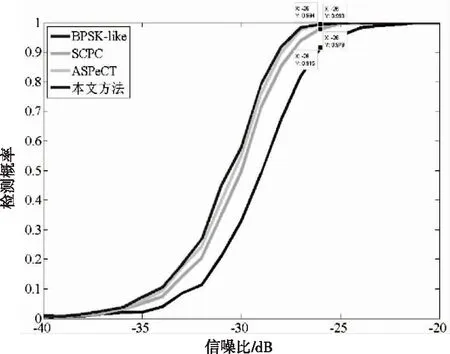
图13 BOC(n，n)检测概率对比

图14 BOC(2n，n)检测概率对比

4.4 峰均比分析

峰均比也是衡量算法性能的主要方式之一。峰均比即检测到的相关函数峰值与平均值的比值。进行20000次蒙特卡罗实验对峰均比进行分析。结果如图15和图16所示。当信噪比为-20dB时，对于BOC(n，n)信号，本文方法相较BPSK-like、SCPC和ASPeCT方法分别提升222.21、192.92和136.8倍。对于BOC(2n，n)信号，分别提升86.95、59.29、2.5倍。因此，本文提出的方法的峰均比值是最高的。

5 结束语

本文提出一种新的适用于sin-BOC(kn，n)的边峰消除方法。本文借助BD B1C采用的BOC(1，1)信号以及GPS L1M采用BOC(10，5)信号进行分析，进而推广至BOC(kn，n)族群。本文提出方法的中心思想是利用时域控制器将本地BOC信号分解成2k段子信号，进而生成子相关。

图15 BOC(n，n)峰均比对比

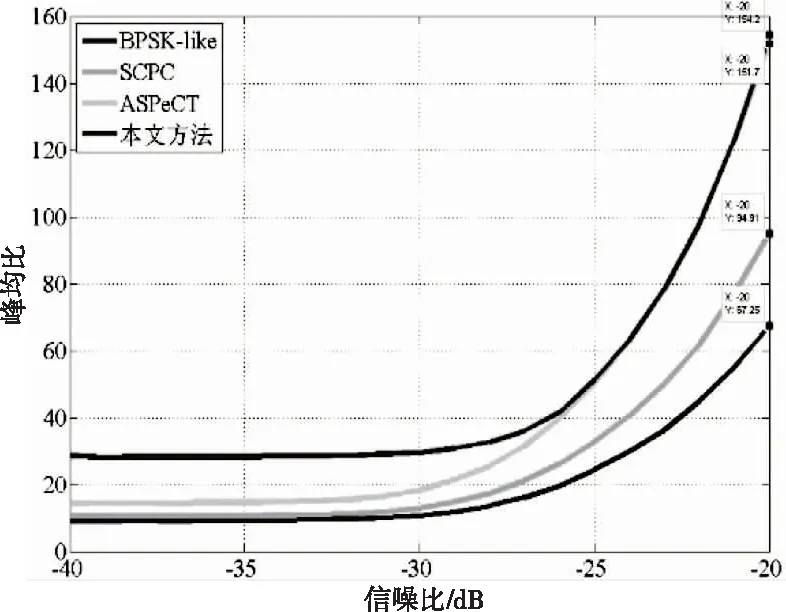
图16 BOC(2n，n)峰均比对比

函数作为辅助相关函数。通过辅助相关函数的非线性组合达到消除边峰的目的。性能分析结果表明，本文提出的方法在消除边峰有效性、鉴相函数曲线、检测概率和峰均比特性中有更优异的表现。而本文方法对BOC(2n，n)信号的检测概率仍有差异。因此，本文提出的边峰消除方法在现代GNSS接收机设计中有一定的参考价值。完成对高阶信号的检测将是下一步的研究方向。