刚性和弹性水锤模型对水轮机调节系统计算的影响

杨帅 徐永 李湧博 王宾 鞠小明

摘要：压力引水系统数学模型是深入分析水轮机调节系统动态特性的一个重要基础，通常以刚性水锤模型或弹性水锤模型来描述压力引水系统，模型的选择和应用基于不同的考虑，精确的模型对系统的稳定性评估、动态计算和控制器优化都具有重要的意义。应用控制理论和数值仿真的方法对选取的水轮机调节系统结构框图进行分析，在此基础上，比较了具有不同惯性比率 R   1 的电站在刚性水锤和弹性水锤这2种水锤模型下的稳定域变化趋势及其过渡过程调节品质的差异。研究结果表明：① 相同惯性比率时，采用弹性水锤模型得到的稳定域要小于刚性水锤模型所得到的稳定域，随着 θ  r  的增加，2种水锤模型下调节系统稳定域的差别会越来越大;② 调速器参数相同时只有在 R   1 较大且 θ  r  大于1的情况下，2种水锤模型下的系统调节品质才会有明显差异;③ 水锤模型的选取宜根据 R  1 和θ  r  的值予以综合判断后再做决定。

关 键 词：刚性水锤; 弹性水锤; 水轮机调节系统; 惯性比率; 数值仿真; 稳定域; 动态特性

中图法分类号：  TV734.1

文献标志码：  A

DOI： 10.16232/j.cnki.1001-4179.2022.03.021

   0 引 言

水轮机调节系统是由调速器和调节对象组成。调节对象包括压力引水系统、水轮机、发电机及其负载，它们都对系统的动态特性具有重大影响。压力引水系统中的水锤是导致调节系统动态特性恶化的一个重要因素，构建压力引水系统的数学模型是深入分析调节系统动态特性的基础  [1] 。在分析水轮机调节系统动态特性时，经常采用刚性水锤或弹性水锤模型，刚性水锤模型由于具有简单性而被广泛应用;而弹性水锤模型因考虑了水的可压缩性和管道的弹性而更接近实际  [2-4] 。针对不同的系统条件，模型的选择和应用有不同的考虑，精确的水轮机调节系统数学模型不仅是水轮发电机组仿真和水力过渡过程的基础，而且对系统的动态计算、稳定性评估和控制器优化都具有重要意义  [5-6] 。

关于2种水锤模型对水轮机调节系统动态特性的影响，皮沃瓦洛夫  [7] 认为，当管道水流惯性时间常数 T  w 远大于管道反射时间T  r 时，可忽略弹性影响，按刚性水锤计算。肖天铎等  [8] 比较了计入和不计入弹性影响的调速器参数稳定曲线，认为对于理想水轮机，在负荷自调节系数e  g 为1的情形下，当机组惯性时间常数 T   a ≥2.5 T   r 时，可按刚性水锤计算;在负荷自调节系数 e   g 为0情形下，当 T   r / T   w ≤1时，可按刚性水锤计算。沈祖诒  [9] 认为以弹性水锤考虑时水轮机调节系统稳定域略有收缩，只有在 θ   r >1  θ    r = T   r / T   w ）时稳定域才有较大变化。杨开林  [10] 认为，随着相对时间常数 τ   l （ τ   l = T   r /（ e   qh  T   w ））的增加，水轮机调节系统稳定域逐渐缩小，在 τ   l ≤1的范围内，此时可以忽略水流和管道弹性的影响。鲍海艳等  [11] 通过对不同水锤波速下水轮机调节系统稳定域的对比，认为水锤波速对稳定域的影响有限，弹性水锤模型和刚性水锤模型下得到的稳定域差别不大，因此可以采用刚性水锤模型对稳定域进行理论分析。孔昭年等  [12] 比较了2种水锤模型下水轮机调节系统稳定边界和过渡过程动态品质的差异，认为当 T   r / T   w 较小时，2种水锤模型下的调节系统稳定边界十分接近，且过渡过程动态特性几乎一致，此时采用刚性水锤模型描述水轮机压力引水系统既简化了模型，又能够得到满意的计算结果。综上所述，目前的研究成果中，基本上都认为 T   r 大于 T   w 时，2种模型下的调节系统稳定域才有明显差异;肖天铎等  [8] 的研究还考虑了 T   a 与 T   w 的比值对稳定域的影响，但没有分析2种水锤模型对调节系统动态品质的影响;孔昭年等  [12] 的研究中，比较了 T   r / T   w 的值对2种水锤模型下水轮机调节系统稳定域和过渡过程动态品质的区别，但没有分析 T   a 与 T   w  的相对关系对不同水锤模型下调节系统动态特性的影响。

在水轮机调节系统中，  T   w 和 T   a 对调节系统的稳定和动态品质起着十分重要的作用。由不同类型的水轮机构成的水轮发电机组有着不同的惯性比率特性， T   w 与 T   a 的比值 R   1 称为水轮发电机组惯性比率， R   1 是调速器参数设计的重要依据，更是影响调节系统动态特性的重要参数  [13-14] 。针对2种水锤模型对不同惯性比率水电机组水轮机调节系统稳定性的影响问题，本文对水轮机调节系统结构框图中的压力引水系统部分，分别应用刚性水锤模型和弹性水锤模型，分析比较了具有不同惯性比率 R   1 的电站在2种水锤模型下的稳定域变化趋势和过渡过程调节品质的差异，并根据研究结果与一些典型电站的 R   1 和 θ   r  的值對水锤模型的适用情况给出了相宜的建议。

1  水輪机调节系统及不同水锤模型的传递函数

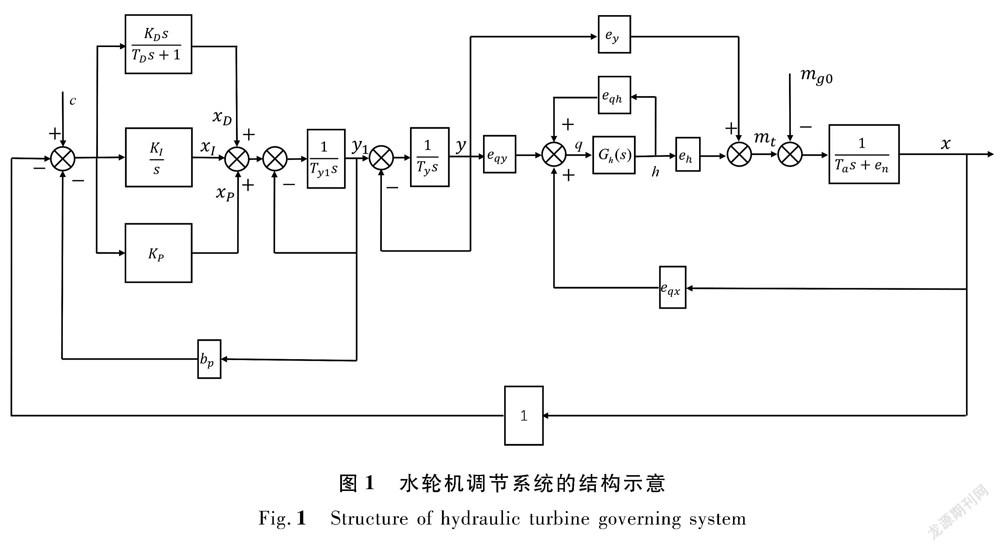
具有并联PID调速器的水轮机调节系统结构框图如图1所示  [9，15] 。

图1中：  m   g0 为负荷扰动;c为转速给定信号; K   P 、 K   I 、 K   D 分别为调节器的比例增益、积分增益、微分增益; T   D 为微分时间常数， s ; b   P 为永态转差系数; T   y1 为辅助接力器响应时间常数， s ; T   y 为主接力器响应时间常数， s ; e   qy 、 e   h 、 e   y 、 e   qh 、 e   qx 为水轮机的传递系数; T   a 为机组惯性时间常数， s ; e   n 为机组自调节系数;s为拉普拉斯算子;x为发电机转速偏差相对值; m   t 为水轮机力矩偏差相对值; y   1 为辅助接力器位移偏差相对值;y为主接力器位移偏差相对值;h为水头偏差相对值;q 为流量偏差相对值;各参数的偏差相对值均以额定值为基准值。

对于压力引水系统，忽略摩擦阻力，按刚性水锤和弹性水锤考虑时，引水系统的传递函数  G   h1 （s）、 G   h2 （s） 如下  [15] ：

G  h1 （s）=-T ws （1）

G  h2 （s）=-h w T rs+ 1 24 T r   3s 3 1+ 1 8 T r   2s 2+ 1 384 T r 4s 4  （2）

式中： T  w 为水流惯性时间常数， s ;T  r 为管道反射时间， s ;T  r =2L/a，L为引水管道的长度， m ;a为水锤波速， m/s ; h   w  为管道特性常数。

2  2种水锤模型下水轮机调节系统稳定域分析

2.1 稳定域

由于采用弹性水锤模型时，水轮机调节系统的传 递函数表达式比较复杂，难以用代数法来研究它的稳定域，因此对图1所示的水轮机调节系统进行了简化。设  b   p =0， T   y1 =0  s ， T   y =0  s ， e   qx =0， T   D  =0 s  [9，16] ，利用梅森公式求解简化后系统的总传递函数  [17] ，从而得到基于刚性水锤模型的系统总传递函数如下：

G 1（s）= a 0s 2-s b 0s 3+b 1s 2+b 2s+b 3  （3）

式中： a 0=-e  qh T w;

b 0=e  qh T aT w+e  qh e yK DT w-e he  qy K DT w;

b 1=e yK D+e ne  qh T w+T a+e  qh e yK PT w-e he  qy K PT w;

b 2=e yK P+e n+e  qh e yK IT w-e he  qy K IT w;

b 3=e yK I。

得到基于弹性水锤模型的系统总传递函数如下：

G 2（s）= c 0s 5+c 1s 4+c 2s 3+c 3s 2+c 4s d 0s 6+d 1s 5+d 2s 4+d 3s 3+d 4s 2+d 5s+d 6  （4）

式中： c 0=-T r 4;

c 1=-16e  qh h wT r 3;

c 2=-48T r 2;

c 3= -384 e  qh h wT r;

c 4=-384;

d 0=T aT r 4+e yK DT r 4;

d 1=e yK PT r 4+16e  qh h wT aT r 3+e nT r 4+16e  qh e yh wK DT r 3-16e he  qy h wK DT r 3;

d 2=48e yK DT r 2+e yK IT r 4+16e ne  qh h wT r 3+48T aT r 2+16e  qh e yh wK PT r 3-16e he  qy h wK PT r 3;

d 3=48e yK PT r 2+384e  qh h wT aT r+48e nT r 2+16e  qh e yh wK IT r 3-384e he  qy h wK DT r+384e  qh e yh wK DT r-16e he  qy h wK IT r 3;

d 4=384e yK D+48e yK IT r 2+384e ne  qh h wT r+384T a+384e  qh e yh wK PT r-384e he  qy h wK PT r;

d 5=384e yK P+384e n+384e  qh e yh wK IT r-384e he  qy h wK IT r;

d 6=384e yK I。

由總传递函数可以得到以下2种水锤模型下系统的特征方程  D   1 （s）、 D   2 （s）：

D 1（s）=b 0s 3+b 1s 2+b 2s+b 3=0 （5）

D 2（s） =d 0s 6+d 1s 5+d 2s 4+d 3s 3+d 4s 2+d 5s+d 6  =0  （6）

根据Routh-Hurwitz稳定判据可得到系统的稳定条件  [17] 。

基于刚性水锤模型系统的稳定条件如下：

（1） 各项系数大于0，即  b   0 >0， b   1 >0， b   2 >0， b   3 >0 ;

（2） Hurwitz行列式>0，即Δ  2 =  b   1  b   2 - b   0  b   3 >0 。

基于弹性水锤模型系统的稳定条件如下：

（1） 各项系数大于0，即  d   0 >0， d   1 >0， d   2 >0， d   3 >0， d   4 >0， d   5 >0， d   6 >0 ;

（2） Hurwitz行列式>0，即 Δ   2 =  d   1  d   2 - d   0  d   3 >0 ，

Δ    3 =- d   4   d   1    2 + d   2  d   1  d   3 + d   0  d   5  d   1 - d   0   d   3    2 >0，

Δ    4 =-  d   0    2   d   5    2 - d   6  d   0  d   1  d   3 +2 d   0  d   1  d   4  d   5 + d   0  d   2  d   3  d   5 - d   0   d   3    2  d   4 + d   6   d   1    2  d   2 -  d   1    2   d   4    2 - d   1   d   2    2  d   5 + d   1  d   2  d   3  d   4 >0，

Δ    5 =-  d   0    2   d   5    3 -3 d   0  d   1  d   3  d   5  d   6 +2 d   0  d   1  d   4   d   5    2 + d   0  d   2  d   3   d   5    2 + d   0   d   3    3  d   6 - d   0   d   3    2  d   4  d   5 -  d   1    3   d   6    2 +2  d   1    2  d   2  d   5  d   6 +  d   1    2  d   3  d   4  d   6 -  d   1    2   d   4    2  d   5 - d   1   d   2    2   d   5    2 - d   1  d   2   d   3    2  d   6 + d   1  d   2  d   3  d   4  d   5 >0。

2.2 计算验证

以锦屏二级水电站的参数为例，  T   w  为1.35 s，  T   a  为9.73 s，引水管道长度 L 为556 m，取水锤波速 a 为 1 000  m/s，则  T   r  为1.11 s，水轮机参数取理想水轮机参数  e   y  为1.0，  e   qy  为1.0，  e   qh  为0.5，  e   h  为1.5  [9，16] 。当水电站在孤网或小网下带负荷运行时，自平衡能力差，微小的负荷变化将影响过渡过程的品质  [18] ，所以取  e   n  =0。得到刚性水锤模型和弹性水锤模型下以调速器参数  K   P 、 K   I 、 K   D  為变量的稳定域图，曲面与坐标轴平面包围的区域为稳定区域，如图2所示。

为了验证本文所列调节系统稳定域的条件，采用Simulink仿真工具搭建了系统仿真模块，在图2中取5个点进行  m   g0  为-0.05的小波动过渡过程模拟。验证计算的特征点位置如表1所列，过渡过程计算模拟情况分别如图3和图4所示。

由动力系统稳定域理论可知：当系统受到小扰动后，参数取值位于稳定域边界上波动是等幅振荡的;参数取值位于稳定域边界外波动是发散的;参数取值位于稳定域边界内波动是稳定收敛的  [11] 。由图3和图4可知：2种水锤模型下的计算结果都满足在稳定域内的点是收敛的，在稳定边界上的点是等幅振荡的，在稳定域外的点是发散的。这也证明了本文分别给出的刚性水锤稳定条件和弹性水锤条件下的稳定域是正确的。

2.3 调节系统稳定域分析

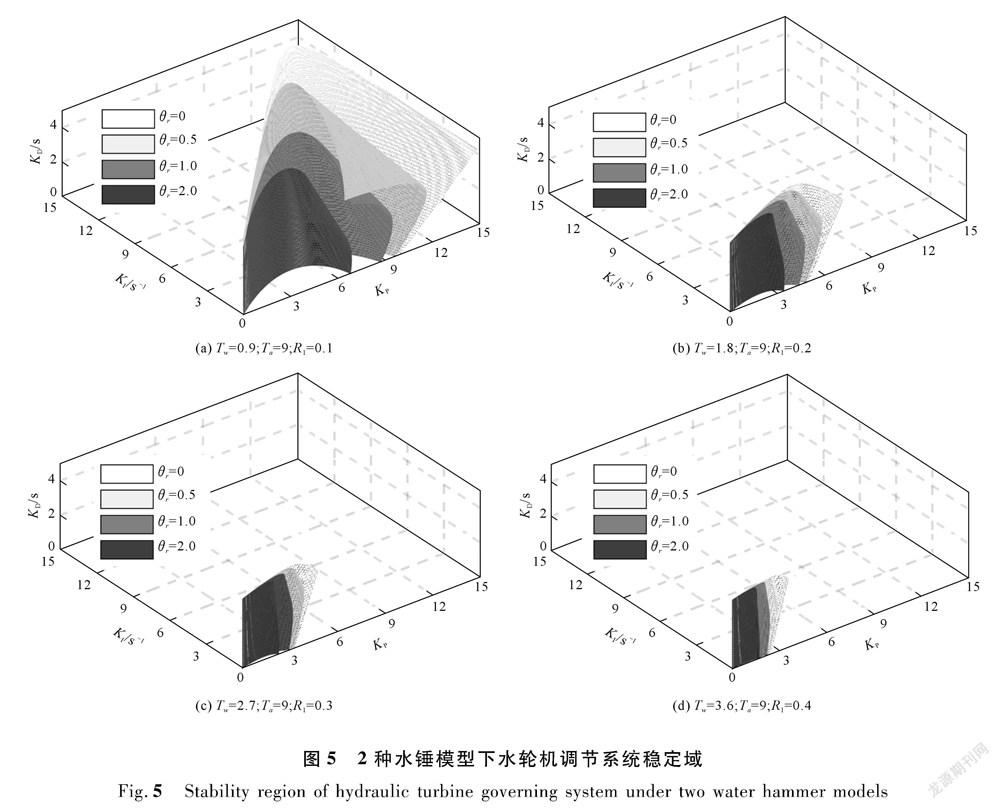
根据本文得出的水轮机调节系统稳定条件，研究 不同惯性比率下刚性 和弹性水锤模型对稳定域的影   响。分别取  R    1 为0.1，0.2，0.3，0.4，仍然令  θ   r 为 T   r / T   w ，对应每一个 R   1 取 θ   r  为0，0.5，1.0，2.0分别计算。当  θ   r  为0时，就是刚性水锤模型，它们的稳定域如图5所示。由图5可知：随着机组惯性比率  R    1 的增加，水轮机调节系统稳定域逐渐缩小，表明水流的惯性不利于调节系统稳定，机组的惯性则相反;在同样的  R    1 时，弹性水锤模型下的调节系统稳定域总是比刚性水锤模型下的稳定域要小，随着  θ   r  的增大，两者的差别越来越大。

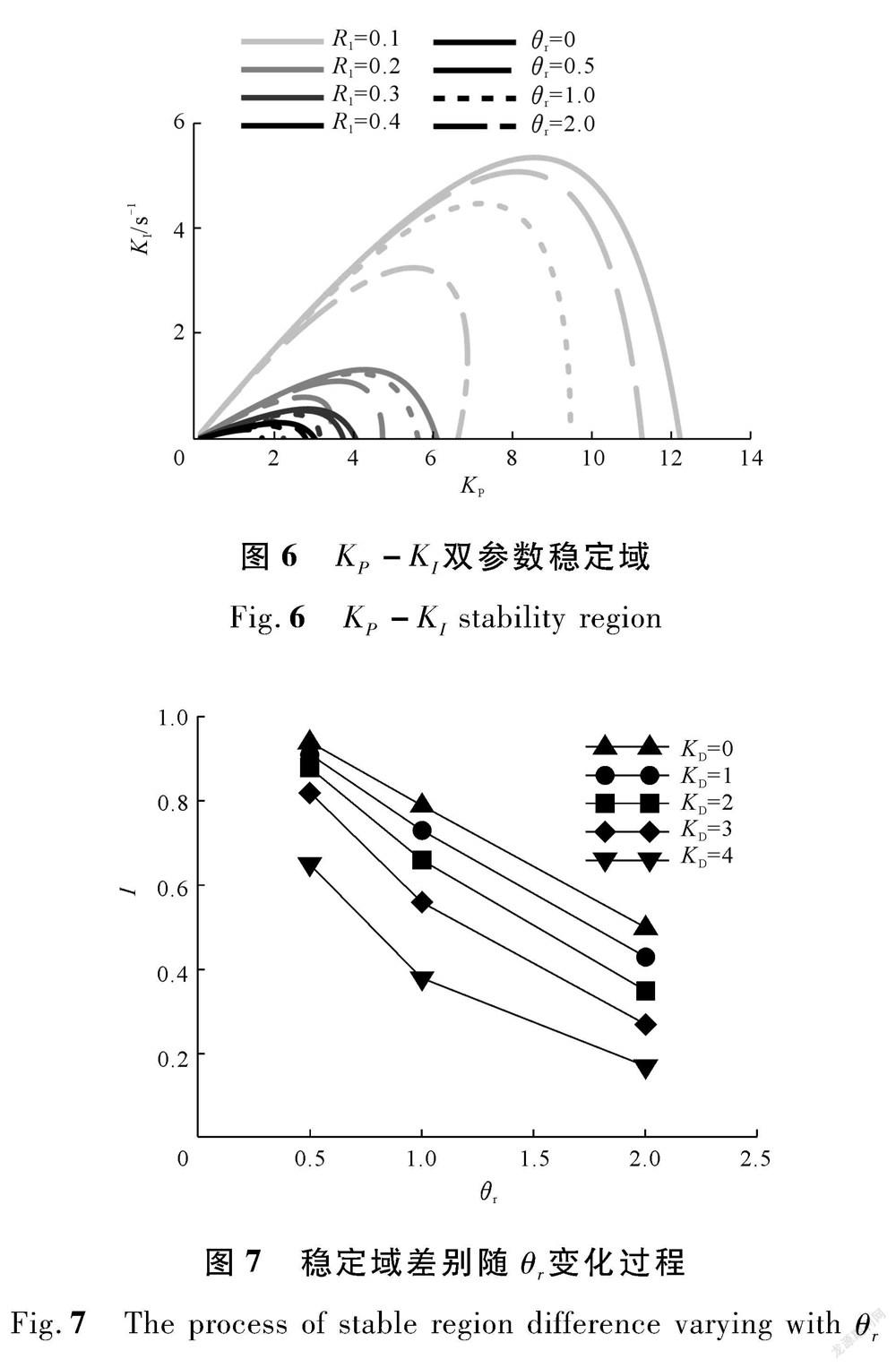
为了研究2种水锤模型下稳定域的差别与  R   1 的关系，取R  1  为0.1，0.2，0.3，0.4，对应每一个  R   1 取θ  r  为0，0.5，1.0，2.0，对应每一组  R   1 和 θ   r 分别取 K   D  为1，2，3，4 s，可以计算出调节系统在2种水锤模型下的  K   P - K   I 双参数稳定域，图6是 K   D 为2时的 K   P - K   I 双参数稳定域。采用梯形积分的方法计算出 K   P - K   I 双参数稳定域的面积，计算结果如图7所示。图7中，每一个点对应 R   1  的值分别为0.1，0.2，0.3，0.4，其中 I 为弹性水锤模型下双参数稳定域面积与刚性水锤模型下双参数稳定域面积的比值。由图7可知：在  θ   r 一定时无论 R   1 和 K   D  为何值， I 的值均为定值，表明采用弹性水锤模型而使系统稳定域相对于刚性水锤模型减小的比例与机组的惯性比率  R   1 无关，仅与 θ   r 的值即 T   r 与 T   w  的比值有关。  

虽然  R   1 反映了具体某个水电站的引水系统水流惯性和机组惯性的比例大小，但是相同 R   1 下的 T   w 和 T   a 的值可有不同的取值情况，比如图8中的 A、B、C、D  4个水电站，它们的 R   1 均为0.19， T   w 和 T   a 的值各不相同。在 R   1 相同的情况下，刚性水锤模型下的水轮机调节系统稳定域随着 T   w 的减小而略有增大;由于 T   w 不同时 θ   r 不同，故无法比较相同 R   1 时 T   w  的值对弹性水锤模型下的稳定域的影响。

3 水轮机调节系统动态品质分析

对于水轮机调节系统，除稳定性要求外，还要有好 的动态品质即：在阶跃扰动的作用下，转速过渡过程的调节时间  T   p （s） 要短、最大转速偏差  x    max 要小、振荡次数要少  [9] 。根据前述调节系统框图，2种水锤模型下小波动过渡过程模拟计算方程如下。

当有压引水系统采用刚性水锤传递函数  G   h1 （s） 时，水轮机调节系统小波动仿真模型为  [9，15] ：

x · =- e n T a x+ e y T a y+ e h T a h- 1 T a m  g0   x I  . =-K Ix-K Ib py 1+K Ic  x D  . =- K D T D  - e n T a x+ e y T a y+ e h T a h- 1 T a m  g0  - x D T D   y 1  . =- K P T  y1  x+ 1 T  y1  x I+ 1 T  y1  x D+ K P T  y1  c- 1+K Pb p T  y1  y 1 y · = 1 T y y 1- 1 T y y   （7）

h · = - e  qx  e  qh   - e n T a x+ e y T a y+ e h T a h- 1 T a m  g0  -   e  qy  e  qh    1 T y y 1- 1 T y y - 1 e  qh T w h （8）

當有压引水系统采用弹性水锤传递函数  G   h2 （s） 时，为了方便地求解高阶函数，将四阶函数转化为4个一阶函数，  h   1 即水头变量h， h   2 、 h   3 、 h   4  为中间变量。

h 1= 1 s h 2- 16T w T rs q h 2= 1 s h 3- 48 T 2 rs h 1 h 3= 1 s h 4- 384h w T r 3s q h 4=- 384 T 4 rs h 1   （9）

公式（9）经过拉氏逆变换写成一阶微分方程形式  [2，15] ：

h ·  1=- 16h we  qx  T r x- 16h we  qy  T r y- 16h we  qh  T r h+h 2  h 2  · =- 48 T r 2 h 1+h 3  h 3  · =- 384h we  qx  T r 3 x- 384h we  qy  T r 3 y- 384h we  qh  T r 3 h 1+h 4  h 4  · =- 384 T r 4 h 1    （10）

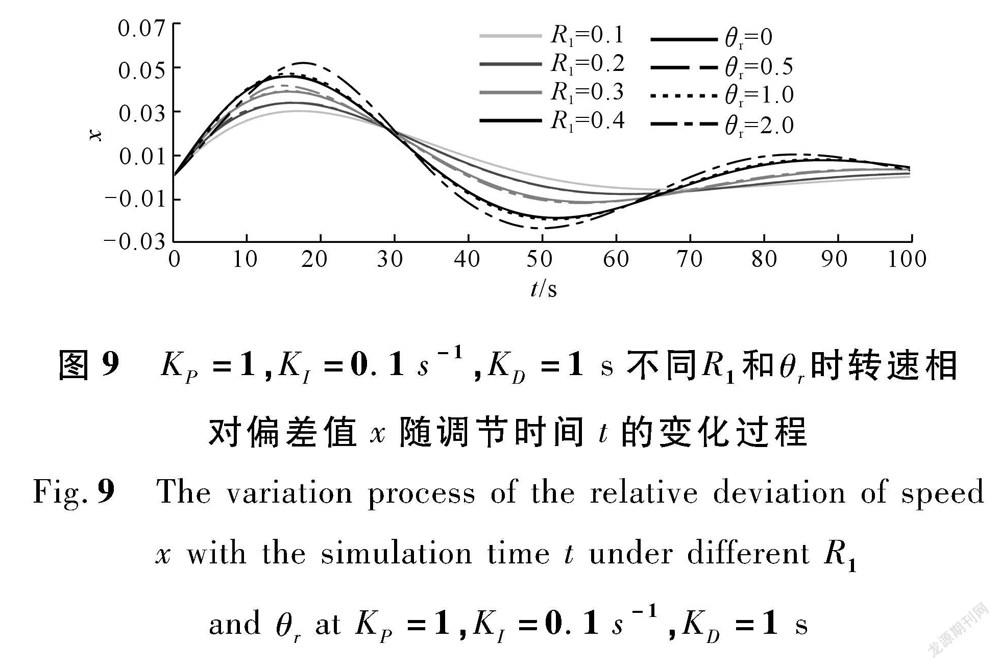
公式（10）就是采用弹性水锤模型的水轮机调节系统小波动仿真模型。为了比较采用2种不同水锤模型的水轮机调节系统的动态品质，取调速器参数 K   P 为1， K   I 为0.1   s    -1 ， K   D 为1.5  s 和K  P 为1.5， K   I 为0.1   s    -1 ， K   D 为2  s ，在这些参数下， R   1 为0.1～0.4和θ  r 为0～2的水轮机调节系统都可以稳定，利用推导的式（7）～（8）进行小波动过渡过程仿真，其中 e   n 为0， b   p 为0， T   y1 为0.01  s ， T   y 为0.02  s ， m   g0 为-0.05， T   D 为0.02  s   [9，16] ，水轮机传递系数采用理想水轮机参数，结果分别如图9和图10所示。由图9和图10可知：当 θ   r 和调速器参数一定时，随着 R   1 的增加系统的调节时间、最大转速偏差和振荡次数均增加，说明水流惯性时间常数越大系统动态品质越差。当 R   1 较小时， θ   r 的值对系统的动态品质基本无影响;当 R   1 较大时，在 θ   r ≤1时的波动曲线差异较小， θ   r >1时的系统动态品质才明显变差。由此表明：水轮机调节系统动态品质主要与 R   1 和调速器参数设置有关，只有在 R   1 较大时，2种水锤模型对系统动态品质的影响才体现出来，且在 θ   r 大于1时这种影响不可忽略。

4 典型电站  R    1 和  θ     r  數据分析及水锤模型选择

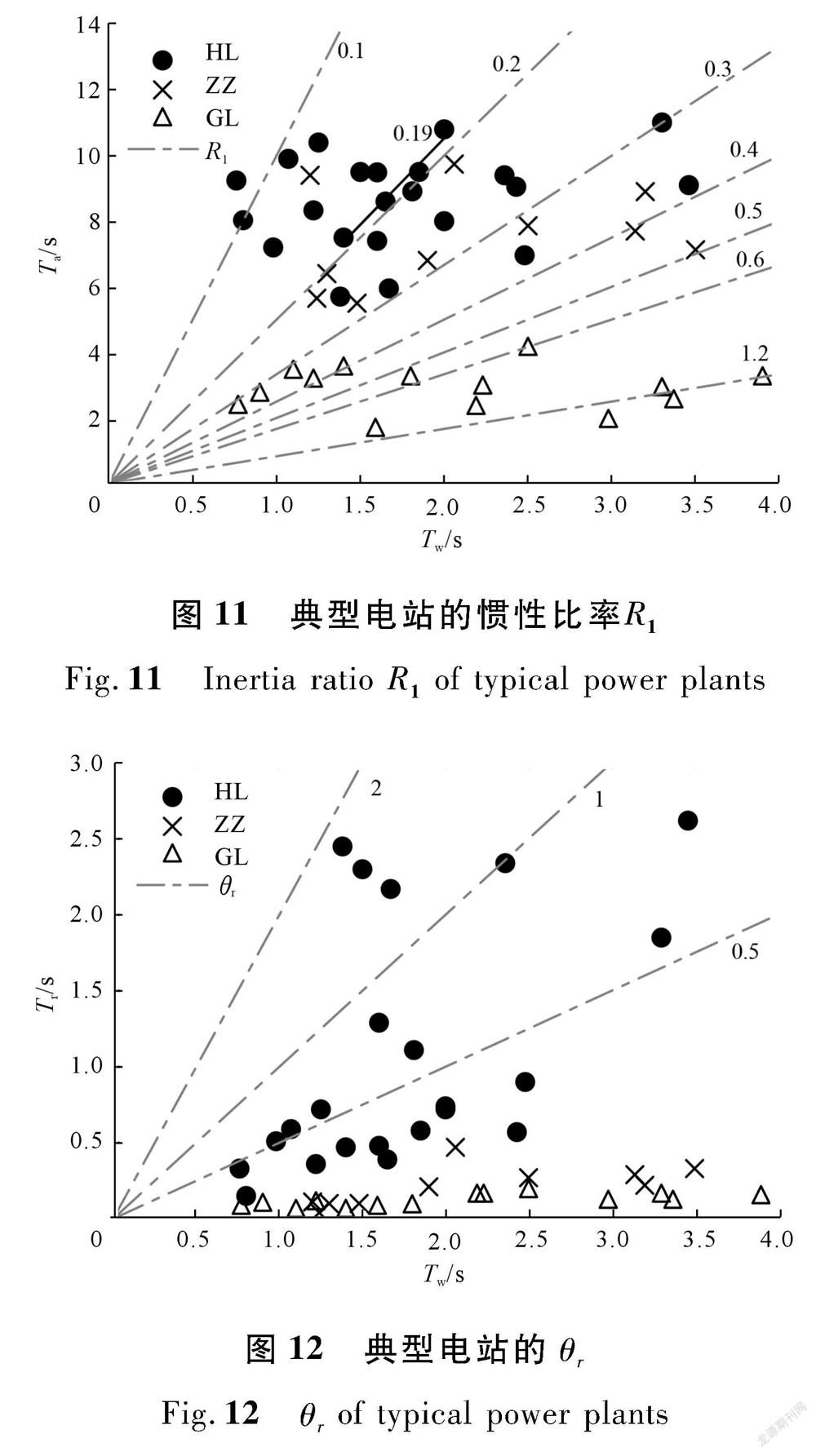
通过对中国典型电站的参数统计，获得如图11所示的典型电站参数范围。图11中的数据来源于文献 [19] ，包含了22个混流式（HL）机组，9个轴流转桨式（ZZ）机组，14个贯流式（GL）机组。由于未能统计到图11中典型电站的实际压力管道数据，图12中的  T   r 是由 T   w =LV/gH和 T   r =2L/a 联立求解得到的  [16] 。其中， g =9.81 m/ s   2 ;波速 a =1 000 m/s  [16] ; L 为压力钢管长度;压力钢管中的经济流速为4～5 m/s，取 v =4 m/s  [20] ; H 为电站的水头。图11中混流式机组的  R   1  均值为0.21，  θ   r  均值为0.61;轴流转桨式机组的  R   1  均值为0.29，  θ   r  均值为0.1;贯流式机组  R   1  均值为0.82，  θ   r  均值为0.06。大多数混流式和轴流转桨式机组的惯性比率较小，贯流式机组的惯性比率一般较大;轴流转桨式机组、贯流式机组的  θ   r  都小于0.5，混流式机组的  θ   r  范围较广，部分机组的  θ   r  大于1。根据前述研究，贯流式机组的  R   1  一般较大，但其  θ   r  小于0.5;轴流转桨式机组的  R   1 和 θ   r 都比较小，对 R   1 和 θ   r  都比较大，宜采用弹性水锤模型来分析水轮机调节机系统的特性。

5 结 论

本文研究了刚性水锤模型和弹性水锤模型对水轮机调节系统的影响，从理论上分析比较了具有不同惯性比率  R    1 的电站在刚性水锤模型和弹性水锤模型2种水锤模型下稳定域变化趋势和过渡过程调节品质的差异，得到以下研究结论：

（1） 无论是刚性水锤模型还是弹性水锤模型，随着水轮发电机组惯性比率  R   1 的增加，水轮机调节系统稳定域缩小;相同惯性比率时，采用弹性水锤模型得到的稳定域小于刚性水锤模型，随着 θ   r 的增大，2种模型得到的稳定域差别会越来越大;采用弹性水锤模型得到的稳定域相对于刚性水锤模型减小的比例与机组的惯性比率 R   1 无关，仅与 θ   r 有关;相同惯性比率时， T   w  越小，刚性水锤模型下的水轮机调节系统稳定域越大。

（2） 水轮机调节系统动态品质主要与  R   1 和调速器参数设置有关，调速器参数相同时只有在 R   1 较大且 θ   r  大于1的情况下，2种水锤模型下的系统调节品质才有明显差异。

（3） 水锤模型的选取宜根据  R   1 和 θ   r 的值来判断。对贯流式机组和轴流转桨式机组采用刚性水锤模型，能很好地描述压力引水系统，还便于计算;对于部分混流式机组， R   1 和 θ   r  都比较大，因此，在分析这类机组的调节系统特性时，宜采用弹性水锤模型。

参考文献：

[1]  陈帝伊.水轮机调节系统[M].北京：中国水利水电出版社，2019.

[2] LI C，CHANG L，HUANG Z，et al.Parameter identification of a nonlinear model of hydraulic turbine governing system with an elastic water hammer based on a modified gravitational search algorithm[J].Engineering Applications of Artificial Intelligence，2016，50：177-191.

[3] MA T，WANG B.Disturbance observer-based Takagi-Sugeno fuzzy control of a delay fractional-order hydraulic turbine governing system with elastic water hammer via frequency distributed model[J].Information Sciences，2021，569：766-785.

[4] WU X，XU Y H，LIU J，et al.Characteristics analysis and fuzzy fractional-order PID parameter optimization for primary frequency modulation of a pumped storage unit based on a multi-objective gravitational search algorithm[J].Energies，2020，13（1）.

[5] 郭海峰.长引水隧洞水电机组系统建模与控制策略优化研究[D].武汉：武汉大学，2017.

[6] 陳志环.水轮机调节系统的参数辨识与控制策略研究[D].武汉：华中科技大学，2017.

[7] 皮沃瓦洛夫.水轮机调节系统的设计与计算[M].连希德，译.哈尔滨：机械工业部哈尔滨大电机研究所，1986.

[8] 肖天铎，董兴林.弹性水锤对水电站调节稳定性的影响[J].中国科学，1982（3）：278-289.

[9] 沈祖诒.水轮机调节[M].3版.北京：中国水利水电出版社，1988.

[10]  杨开林.电站与泵站中的水力瞬变及调节[M].北京：中国水利水电出版社，2000.

[11] 鲍海艳，龙丽婷，付亮，等.水轮机调速器功率调节模式下负荷调节过渡过程稳定性研究[J].农业工程学报，2019，35（17）：50-57.

[12] 孔昭年，田忠禄，张振中，等.水击模型对水轮机调节系统过渡过程特性的影响[J].水电站机电技术，2015，38（9）：1-4，71.

[13] 魏守平.水轮发电机组的惯性比率[J].水电自动化与大坝监测，2011，35（4）：31-34，42.

[14] 孔昭年.水轮机PID调速器微分环节的设计计算和参数测试方法[J].大电机技术，1983（6）：50-56，2.

[15] 陈嘉谋.水轮机调节系统计算机仿真[M].北京：水利电力出版社，1993.

[16] 魏守平.水轮机调节系统仿真[M].武汉：华中科技大学出版社，2011.

[17] 胡寿松.自动控制原理[M].5版.北京：科学出版社，2006.

[18] 沈钊根，周延波.水电站小波动过渡过程的稳定性评价分析[J].西北水电，2020（4）：89-92.

[19] 关欣.大惯性比率水电机组对现代电力系统稳定性的影响[D].西安：西安理工大学，2018.

[20] 中华人民共和国水利部.小型水力发电站设计规范：GB 50071-2014[S].北京：中国计划出版社，2014.

（编辑：赵秋云）

Influence of rigid and elastic water hammer models on calculation of  hydraulic turbine governing system

YANG Shuai 1，XU Yong  1，2 ，LI Yongbo 1，WANG Bin 3，JU Xiaoming  1，2

（ 1.School of Water Resources and Hydropower，Sichuan University，Chengdu 610065，China; 2.State Key Laboratory of Hydraulics and Mountain River Engineering，Sichuan University，Chengdu 610065，China; 3.Sichuan Water Conservancy College，Chongzhou 611231，China ）

Abstract：

The mathematical model for pressure water diversion system is an important tool for in-depth analysis of the dynamic characteristics of hydraulic turbine regulation system.Pressure water diversion system is usually described by rigid water hammer model or elastic water hammer model，which is depend on different consideration，and accurate model has important significance for system stability evaluation，dynamic calculation and controller optimization.In this paper，the control theory and numerical simulation were used to analyze the structure flowchart of selected turbine regulation system，then the trend of stability domain and transition regulation quality of hydropower stations with different unit inertia ratio（ R 1 ） were compared by using rigid water hammer model and elastic water hammer model.The results showed that ① When the unit inertia ratio was the same，the stability region of the elastic water hammer model was smaller than that of the rigid water hammer model，with the increasing of  θ r ，the difference of the stability region of hydraulic turbine governing system under the two water hammer models became larger and larger.②When the governor parameters were the same，only when  R 1 was larger and  θ r was greater than 1，there was a significant difference in system regulation quality of the two water hammer models.③ The selection of water hammer model should be judged comprehensively according to the values of  R 1  and  θ r .

Key words：

rigid water hammer;elastic water hammer;hydraulic turbine governing system;unit inertia ratio;numerical simulation;stability region;dynamic characteristics