交易费用影响下带扰动对偶模型的最优分红与注资策略
2022-04-15谢奕,王伟
谢 奕,王 伟
(天津师范大学数学科学学院,天津 300387)
近年来,对偶风险模型受到广泛关注,与经典风险模型[1-4]相比,它适合于连续支出费用且收益随机的公司,如石油勘探公司、研发制药公司,其中收益随机可以解释为未来的某一次发现或发明.许多学者对对偶风险模型进行了研究[5-12].最优分红问题是精算学的热门研究课题之一.文献[5]研究了对偶风险模型的最优分红问题,公司目标为最大化破产前期望分红的折现值,分别得到了在收入额服从指数分布和混合指数分布时的值函数和最优分红策略的表达式.在现实的经济交易市场中,交易费用是一个不可回避的问题,它通常包括2个部分:比例费用和固定费用.如果目标函数中包含固定费用,就会产生一个脉冲控制问题,这个问题可通过使用随机控制方法中的拟变分不等式解决.文献[6]研究了一类对偶模型的最优分红问题,并且分红带有比例和固定交易费用,通过求解相应的拟变分不等式得到了值函数的显式解和最优策略.在实践中,如果没有足够的偿付能力,公司可以从市场上筹集新的资金,以继续经营,因此需要考虑注资问题,这是降低风险的重要途径.文献[7]考虑在对偶模型的最优分红中加入注资,以避免破产,研究目标相应变为最大化期望分红与注资折现之差.
本文在文献[6]的基础上,加入扰动项和最优注资问题,扰动项代表流动资产的微小变动,注资带有比例费用.分析了值函数的性质,建立相应的拟变分不等式,通过求解该拟变分不等式,得到在收入额服从指数分布时的最优策略和值函数的显式解,最后给出数值算例对所得结果进行了分析.
1 最优分红与注资问题
记(Ω,F,P)为概率空间,{B(t),t≥0}是一个标准Brown运动,其中{Ft,t≥0}满足通常性条件.保险公司的盈余过程X(t)为一个对偶模型,即
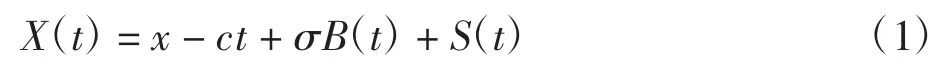
其中:x≥0为初始盈余,c>0为单位时间内的花费速率,σ>0为波动率;为复合Poisson过程,{N(t),t≥0}是参数为λ>0的Poisson过程,{Yk}与{N(t)}相互独立,表示历次的收入额,其一阶矩为μ>0.
定义一个控制策略π=(τi,i=1,2,…;ξi,i=1,2,…;Gt),其中:{τi,i=1,2,…}为一列关于{Ft,t≥0}可测的递增停时,表示分红时间;{ξi,i=1,2,…}为一列非负随机变量,表示在τi时刻支付给股东的分红额;Gt表示从0到t时刻保险公司获得的注资总额.考虑市场交易有摩擦,假设每次分红支付ξi都会产生固定费用K≥0和比例交易额β1ξi,β1≥0为比例分红费用因子.因此,从盈余中扣除的费用为=(1+β1)ξi+K.
在控制策略π下,盈余过程可表示为
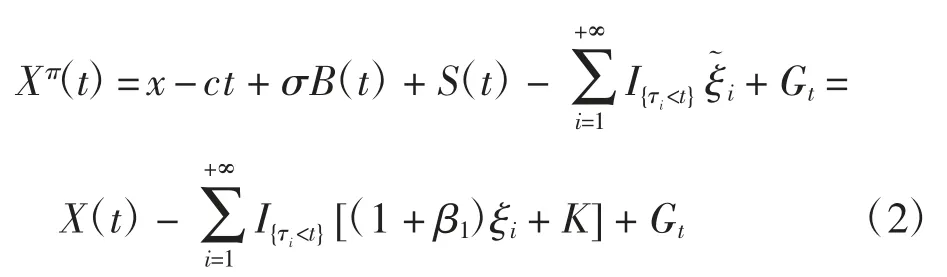
考虑到实际情况,为了使保险公司盈余为正,在公司亏损和盈余小于固定费用K的情况下应禁止分红,即
定义1若控制策略π满足条件:
(1){τi}是一列关于{Ft,t≥0}的停时,且0≤τ1<τ2<…<τi<…,i=1,2,…;
(2)0≤ξi≤(Xπ(τi)-K)/(1+β1)关于{Ft,t≥0}可测,i=1,2,…;
(3){Gt,t≥0}关于{Ft,t≥0}可测;
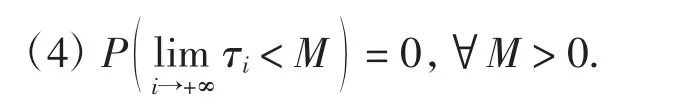
则称π为可行策略,所有可行策略的集合记为Π.
对于每个可行策略π∈Π,相应的目标函数为
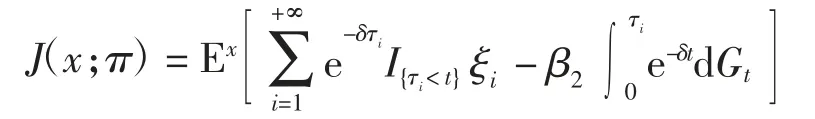
其中:Ex表示初值为X(0)=x的条件期望;δ>0为贴现因子;β2>1为比例注资费用因子.为最大化目标函数J(x;π),需寻求最优策略π*∈Π,使得
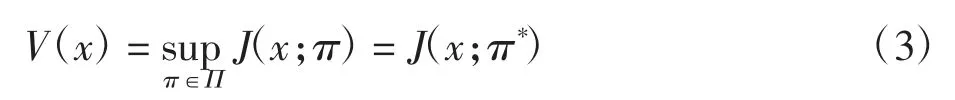
称V(x)为值函数.
2 值函数的性质和拟变分不等式
定理1值函数V(x)满足不等式
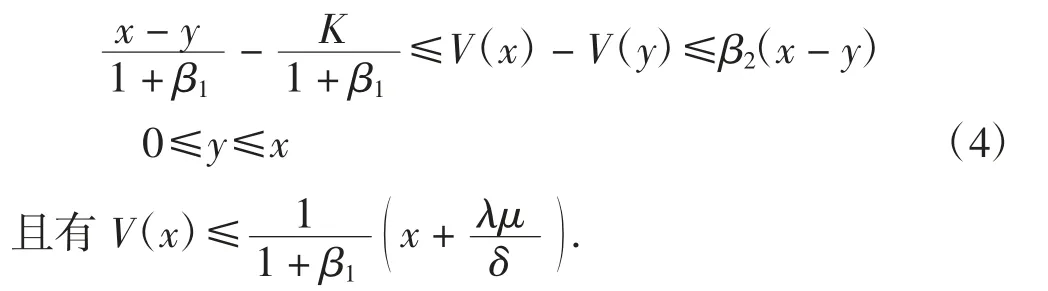
证明对于任意ε>0,存在可行策略π1使得J(y;π1)≥V(y)-ε.对任意初始盈余x≥y,可定义如下可行策略:将x-y立即作为红利分给股东,然后按照策略π1,公司盈余立即变为y.则对于ε>0,有

考虑一种特殊情况:公司没有消耗,即c=0,那么所有的初始盈余和利润都将作为红利分给股东.由于没有消耗,则不需要进行注资.由跳跃时间Tk服从Γ(λ,k)分布,则有
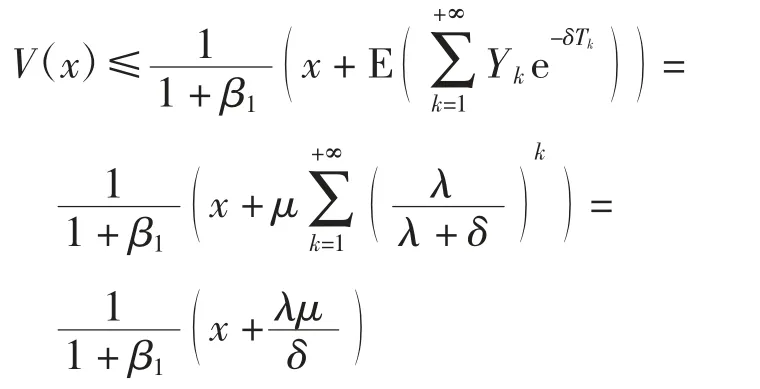
定理证毕.
定义2对于每个在[0,+∞)上的连续函数h,定义如下算子:
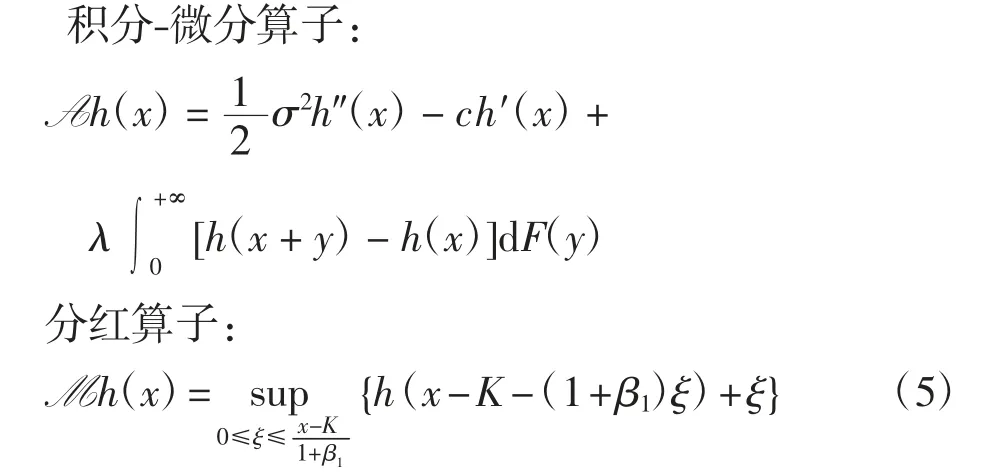
注当初始盈余x∈(0,K)时,由于此时的盈余都不足以支付交易费用,所以不进行分红.若分红策略是最优的,则有Mh(x)=h(x).定义集合Dh={x≥0;h(x)=Mh(x)}.
定义3若在[0,+∞)上的连续函数g(x)满足条件:
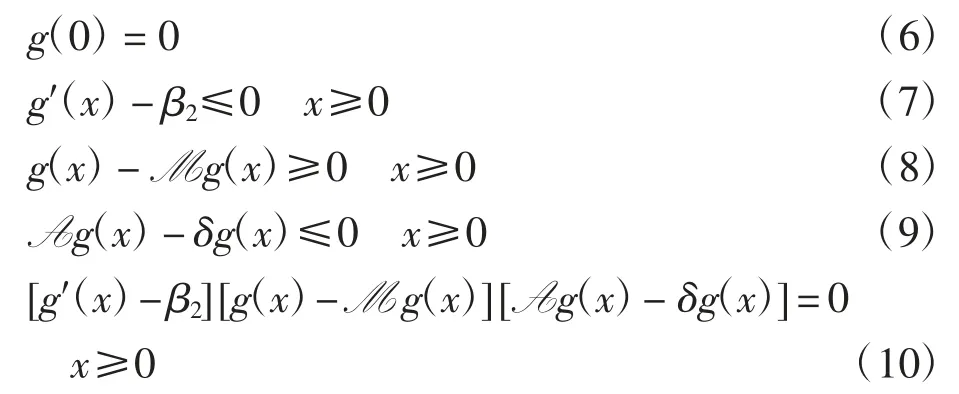
则称g(x)为满足控制问题所对应的拟变分不等式的解.

3 值函数的显式解与最优策略
为得到值函数和最优控制策略,考虑收入额服从指数分布的情形,即

其中Ai,i=1、2、3为常数.
考虑货币的时间价值,尽可能长时间推迟发行新股是最优的,即尽量推迟注资,则有
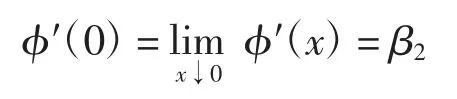
将上式和边界条件ϕ(0)=0代入式(13),整理得
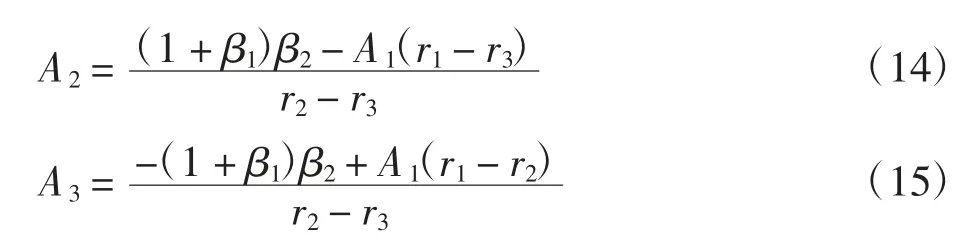
由于存在固定费用,考虑采用双边界最优脉冲控制策略.当盈余没有达到或超过上边界b*时,不支付分红,一旦达到或者超过b*,将超过下边界a*的盈余作为分红支付给股东,则值函数为
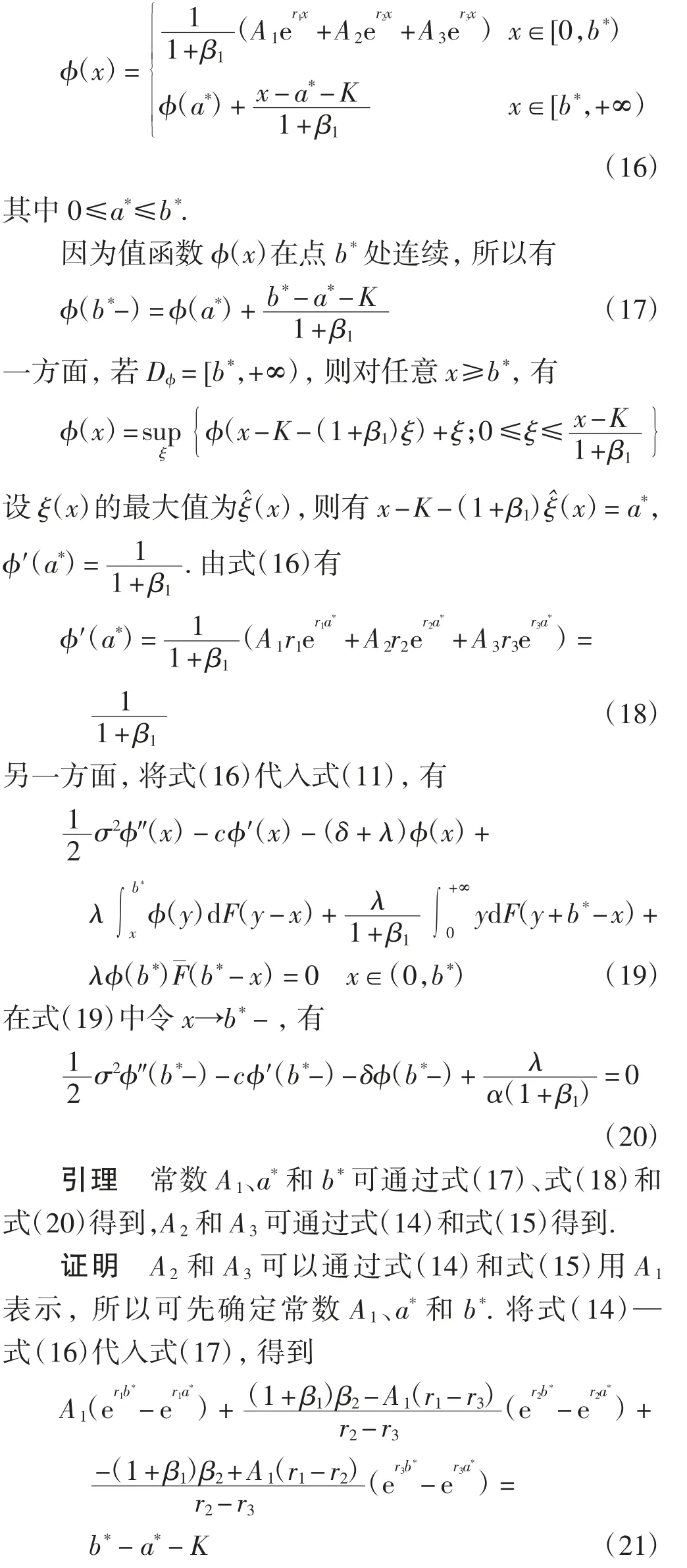

即,当盈余没有达到或超过b*时,不会进行分红,一旦超过b*则进行分红,并且分红额为超过a*的部分.
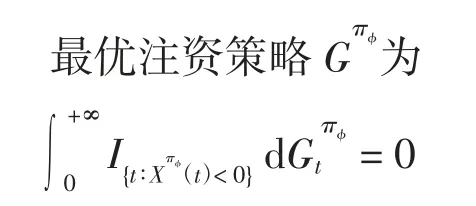
即只有当盈余小于等于0时才进行注资,盈余大于0时不进行注资.
对于最优策略πϕ,有ϕ(x)=V(x)=J(x;πϕ).
证明(1)由定义有V(0)=0,即式(6)成立.
(2)由式(20)有

③对于x≥b*,由定义有MV(x)=V(x).
综上,式(8)成立.
(4)由V(x)的表达式可知,在x∈[0,b*]这个范围内,有AV(x)-δV(x)=0.对于x>b*,有V′(x)=1/(1+β1),则AV(x)=(λμ-c)/(1+β1).利用V(x)在x=b*的连续性可得
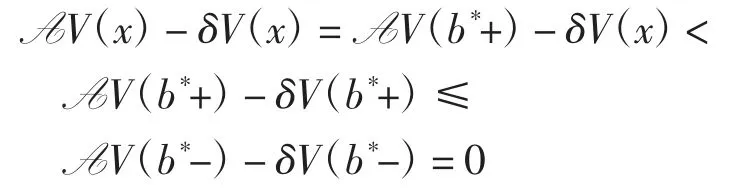
因此式(9)成立.
(5)当x=0时,有V′(x)=β2;当x∈(0,b*)时,有AV(x)-δV(x)=0;当x∈[b*,+∞)时,有MV(x)=V(x).因此式(10)成立.


综上可得,V(x)是满足拟变分不等式(6)—(10)的解,且πϕ为最优策略.定理证毕.
4 数值算例
设c=1,δ=0.1,λ=1,α=0.5,β1=0.01,研究扰动σ、注资比例费用因子β2和分红固定交易费用K对值函数V(x)及双边界策略a*和b*的影响.
情况1取β2=1.1,K=5.当σ=0.5、0.7和0.9时,V(x)的图像见图1.由图1可见,扰动越大,值函数越大,当初始盈余x增大到一定值时,扰动的增加对值函数影响不大.同时,计算得到当σ=0.5、0.7和0.9时,a*=0.201 6、0.223 2和0.250 0,b*=7.957 9、8.321 9和8.766 7,这说明随着扰动的增大,边界a*和b*也增大.
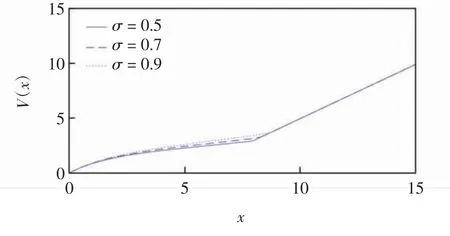
图1 σ分别取0.5、0.7和0.9的值函数Fig.1 Value functions whenσis equal to 0.5,0.7 and 0.9 respectively
情况2取σ=0.8,K=5.当β2=1.1、1.2和1.5时,V(x)的图像见图2.由图2可见,注资比例费用因子越大,值函数越大.同时,当β2=1.1、1.2和1.5时,a*=0.236 0、0.435 2和0.967 8,b*=8.535 1、9.029 7和10.731 8,这说明随着注资比例费用因子的增大,双边界也增大.
情况3取σ=0.8,β2=1.2.当K=1、5和7时,V(x)的图像见图3.由图3可见,分红固定交易费用越大,值函数越小.当K=1、5和7时,a*=0.435 27、0.435 26和0.435 26,b*=3.288 02、9.029 68和12.232 28,这说明当分红固定交易费用增大时,边界策略a*会缓慢减小,边界策略b*会增大.
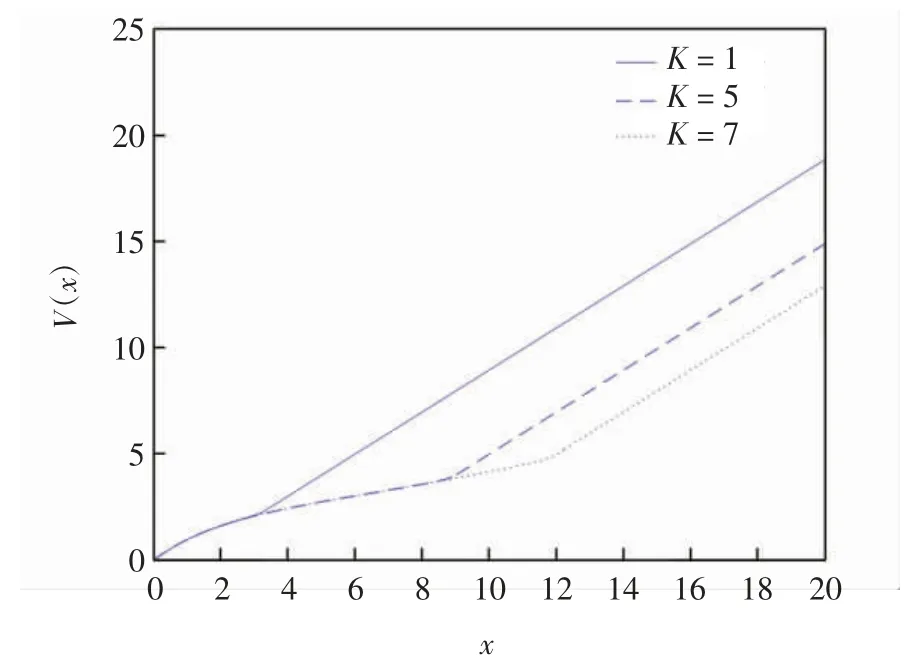
图3 K分别取1、5和7的值函数Fig.3 Value functions when K is equal to 1,5 and 7 respectively
5 结论
本文基于带扰动的对偶风险模型,研究最优分红与注资的控制问题,分红和注资都带有交易费用.通过求解相应的拟变分不等式,得到值函数的显式解和最优策略.数值算例结果表明,扰动、注资和分红的交易费用对值函数和双边界策略均有影响.此外,在本文的基础上,还可以考虑时间偏好不一致模型和注资带有固定交易费用的情况,这是下一步的研究内容.
