多种进化算法混合解决约束工程优化问题研究

李清霞

东莞城市学院 计算机与信息学院，广东 东莞 523419

在科学和工程领域，诸如航班调度和网络负载均衡等问题都是约束优化问题（constrained optimization problem，COP）[1]，并且至今仍是一个具有挑战性的研究领域。由于约束优化问题在科学及工程问题中的重要性，许多处理约束优化问题的算法被提出[2-7]。基于梯度的优化方法作为处理约束优化问题的一个典型方法得到了广泛的应用，但是后来人们发现基于梯度的优化方法不足以解决所有的约束优化问题，特别是对于具有多个局部最优解的优化问题。因此，进化算法应运而生。该类算法不需要使用任何梯度信息，而且更容易实现，更为重要的是其能以最低的计算效率得到最优解。

近几十年来，进化算法得到了空前的发展，特别是能够处理约束优化问题的进化算法，主要包括遗传算法（genetic algorithm，GA）[2]、粒子群优化算法（particle swarm optimization，PSO）[3]、差分进化算法（differential evolution，DE）[4]、蜜蜂算法（artificial bee colony，ABC）[5]、共生生物搜索算法（symbiotic organisms search，SOS）[6]和风驱动水波优 化 算 法（ wind-driven water wave optimization，WDWWO）[7]等。这些进化算法大多数都是受自然启发的，这意味着它们起源于生态系统中生物的行为或相互作用。例如，差分进化算法源自于种群进化选择过程，粒子群优化算法取自生物体的运动行为，共生生物搜索算法来自生态系统中生物体的共生相互作用。在所有进化算法中，都是从初始种群开始搜索，并将其引导到具有更好适应值的解。然而根据“没有免费的午餐”理论[8]，没有哪种单一的进化算法能够对所有的约束优化问题都具有良好的优化效果。这是因为所有进化算法对于约束优化问题求解都存在各自的优势，即不同的进化算法都存在着各自的优缺点，某一类进化算法可能只适合于求解某些类型的约束优化问题，这使得混合多种进化算法求解约束优化问题成为了可能。

混合多种进化算法就是使混合的各算法相互合作，提高求解优化问题的性能[9]。因此许多著名的进化算法的组合已经被提出用于解决约束优化 问 题， 如PSGA[10]、PSO-DE[11]、GWO-DE[12]、HCS-LSAL[13]、HABCDE[14]等。这 些 混合进化 算法（如PSGA）与其他单一的进化算法相比，能够通过较少的函数评估次数就可获得最优解。

为了设计出更好的混合进化算法，则需要了解每一种进化算法的优势和不足，也需要在搜索过程中充分平衡探索和勘探，以获得最佳的搜索结果。探索和勘探本质上是相互矛盾的，如差分进化算法在探索过程中表现良好，那么它在勘探性搜索中就会表现得很弱，反之亦然。粒子群优化算法是一种基于种群的算法，在面对多模态函数时，它往往很快收敛到一个局部极小值，从而错过了全局最优的机会。共生生物搜索算法是一种简单而强大的进化算法，它模拟了生物在生态系统中生存和繁殖所采取的共生互动策略。该算法的主要优点是不需要在算法开始时设置任何特定的参数[6]。利用这种优势，只需设置几个参数就可以与其他进化算法进行混合。差分进化算法在种群择优选择的时候存在偶然性，它按概率进行择优，选择更优的种群进行迭代。另外，粒子群优化算法具有学习策略，即在每次迭代中，它为种群中的每个元素存储最优的子代。共生生物搜索算法虽然没有采用学习策略存储每个生物体的最优解，但它的最优解却会影响下一代的迭代结果。利用每种进化算法的优点，结合它们的进化特性，弥补各自的不足，本文提出了一种混合差分进化、粒子群优化和共生生物搜索的进化算法（简称HDPS）用以解决约束工程优化问题。由于以往混合的进化算法基本上都是两类进化算法的组合，导致了求解约束优化问题的优势并没有完全展现出来。因此我们将差分进化、粒子群优化和共生生物搜索这3 种进化算法结合起来，通过改进的惩罚函数和互利操作控制算法的可行性及多样性，达到求解约束优化工程问题的最佳效果。这3 种算法的结合不仅没有增加执行时间，而且大大减少了执行时间，即HDPS 算法具有较低的时间复杂度。实验结果表明，与其他非混合或混合的进化算法相比，HDPS 算法能够更快地解决大多数约束优化问题，并且具有更高的成功率。

1 相关背景

1.1 约束优化问题

一般搜索空间S中的约束优化问题可由如下几个方面构成[1]：

1）目标函数f(x)；

2）可行解向量x= (x1,x2, … ,xd)；

3）约束变量C=c1,c2, … ,cm为可行解满足的约束条件。

其中d为问题空间维度，m为约束条件个数。一般的约束优化问题可表示为

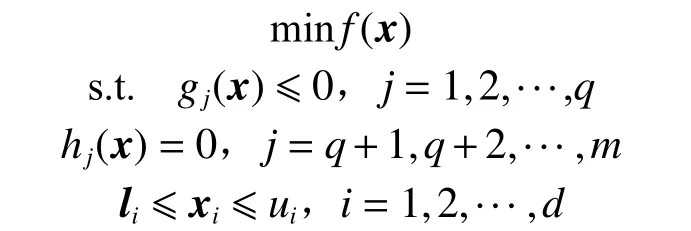
式中：gj(x)≤0 和hj(x)=0 分别表示q个不等式约束和m-q个等式约束，ui和li分别为向量xi的上界和下界。

1.2 差分进化算法

差分进化算法是目前最流行、应用最广泛的基于种群优化的进化算法，依赖于偶然性搜索[4]。在差分进化算法中，种群大小一般设为N，每个种群中包含d维个体向量，t为迭代次数。差分进化算法主要有3 种操作：变异，交叉和选择。

1）变异：通过变异操作随时产生新的目标向量，计算公式为

式中：xi,t=[xi,1,t,xi,2,t,…,xi,d,t]，其中i=1, 2,…,N，t为当前种群的代数；F为缩放因子，是[0, 1]的随机数。

2）交叉：交叉操作主要产生试验变量ui,t，计算公式为

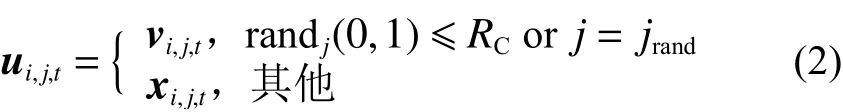
式中：i=1, 2,…,N,j=1, 2,…,d；jrand为[1,d]的一个随机整数；randj(0, 1)为对于每个j产生[0,1]均匀分布的随机数。

3）选择：以一定的概率从种群中选择更优的个体进入下一代。一般，选择过程是一种基于适应度的优胜劣汰的过程。

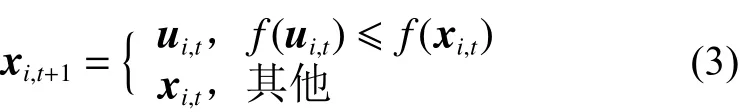
1.3 粒子群优化算法

粒子群优化算法首先是由Kennedy 等[3]提出的，其灵感来源于自然界中鸟类或鱼类等生物的运动行为。它为种群中的每个个体调整策略，以搜索一个目标函数空间。这些个体被称为粒子，并用xi表示。在粒子群优化算法中，首先在搜索空间中建立粒子的初始种群。在d维搜索空间中，每个粒子都有速度，速度用vi表示。每个粒子的最佳位置pbesti和种群的最佳位置gbest在每次迭代中存储和更新，即粒子群优化算法的本质就是利用迭代过程中的运动经验进行最优化求解。假设t是迭代次数，则粒子群优化算法中粒子的速度和位置更新计算为

1.4 共生生物搜索算法

共生生物搜索算法是由Cheng 等[6]提出来的一种进化算法，其灵感来源于生态系统中生存的共生生物。共生生物搜索算法模拟了生态系统中成对生物关系的共生交互行为，试图寻找合适的生物。在共生生物搜索算法中，种群中的个体被称为生物体，每个生物体代表搜索空间中的一个点。共生生物搜索算法的一个显著优势就是不需要在算法开始阶段设置特定的参数，因此共生生物搜索算法比较容易实现，它的主要运算操作是采用类似于生物相互作用的互利共生、偏利共生和寄生操作更新每次迭代中有生物位置。即在每一个阶段，如果这种关系使生物体i或j的适应值更好，生物体的位置就会更新。

1）互利共生：互利共生主义就是对建立共生关系的2 个生物体都有利。例如与种群中第i个成员对应的生物体xi和随机选择的生物体xj建立了共生关系，他们都希望在生态系统中增加彼此的生存优势，并从中受益，则生物体xi和xj的新位置可以表示为

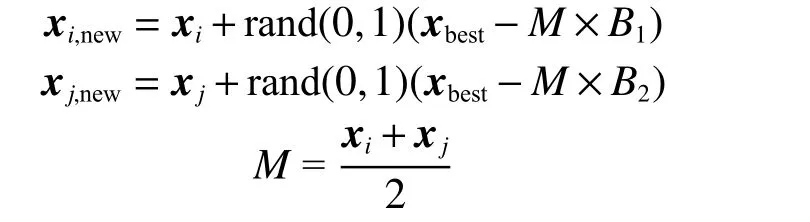
式中：M为生物体xi和xj之间的关系；B1和B2为获益因子，它们表示共生作用对于每个生物体的获益情况，一般随机取值1 或2；xbest为目前为止的最优个体。

2）偏利共生：偏利共生是指对建立共生关系的2 个生物体中的一方有利，另一方不受影响（既不意味着获益也不意味着受害）。与互利共生相似，在这一阶段，生物体xj随机地与生物体xi相互作用，但只有生物体xi受益于共生关系，而对生物体xj没有影响。其更新计算公式为

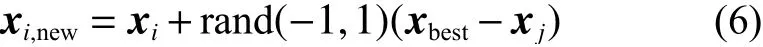
3）寄生：寄生是指对建立共生关系的2 个生物体中的一方有利，同时另一方受害。例如在疟蚊与人的关系中可以看到寄生现象，蚊子有益，人受到伤害。由于在这个阶段有一个生物体受到伤害，就必须杀死受伤害的生物体，并用另一个替代它。此时，随机选择生物体xj作为寄生虫载体的受害者，然后生物体xi在搜索空间中随机选择某些维度创建寄生向量。如果寄生虫载体比选择的xj更好，那么它会杀死xj并占据它的位置；否则xj将对寄生虫有免疫力，并且可以比寄生虫活得更长。

2 混合进化算法HDPS

2.1 算法思想

对于混合进化算法HDPS，采用差分进化算法从父辈选择最优的子代，这有助于粒子群优化算法在更优的子代中找到最优解，并帮助共生生物搜索算法在共生互动中获得更好的生存机会。差分进化算法与共生生物搜索算法组合后，由差分进化算法的变异和交叉操作产生更多优质的种群。共生生物搜索算法将利用这些优质的种群进行迭代，而不是使用自己产生的种群迭代。在通过差分进化算法选择最优种群之后，再使用粒子群优化算法对比邻居种群以获得更好的解。因此在HDPS 算法中，迭代种群中的每一个个体都可以保证是最优的。HDPS 算法步骤也可以这样理解：在每个迭代周期中，首先采用差分进化算法产生初始种群，并运用差分进化算法的变异、交叉和选择操作产生最优子种群xbest，每个子种群包括了速度、位置、代价和最优经验值等4 个参数。然后通过粒子群优化算法检查邻居的解以获得更好的解。在这个阶段，如果位置移动能够为个体带来更好的适应值，那么就更新位置，否则不作任何改变；如果个体的最优适应值优于xbest（全局最优），那么就更新xbest；所以粒子群优化算法通过速度公式检查该区域，并存储每个个体的最优适应值并更新全局最优。最后通过共生生物搜索算法的共生相互作用（互利、偏利和寄生）使它们获得更好的适应值；即如果个体交互得到了更好的适应值，则更新个体的适应值，否则不变。

2.2 改进的惩罚函数

惩罚函数是一种比较简单可行的约束处理技术， 主 要 用 于 控 制1～2 个 约 束 条 件。 但在HDPS 算法中，必须要处理2 个以上的多个约束条件，因此就需要对传统的惩罚函数进行改进以使HDPS 算法有更好的搜索性能。在HDPS 算法中，改进的惩罚函数能够处理多个不等式或等式约束。对于违反约束条件的情况，则设违反约束程度为非零（ki=1），对于没有违反约束条件的情况，则设违反约束程度为零（ki=0）。违反约束计算可表示为

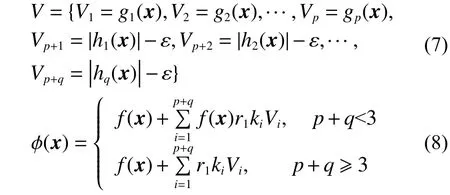
惩罚函数的本质就是将约束问题转化为无约束问题来控制约束，如式(8)所示。在式(7)和式(8)中，φ(x)是新的目标函数，ri是控制参数（违反约束因子），Vi是第i个约束冲突，ε=10-4。当解不可行时，ki=1，否则ki=0。在HDPS 算法中，对于所有求解的问题，违反约束因子ri=10。

2.3 改进的互利操作

为了使共生生物搜索算法在求解问题时获得更好的解，最优个体xbest不需要在所有维度都和M向量做减法运算，而是选择一个随机维度执行减法运算。假设用xbest,r表示最优个体的一个随机维度，Zr为{1, 2,…,d}内的随机整数，d为维度。则采用这种改进的互利操作后，生物体xi和xj不总是朝着最好的方向移动，而是朝着随机的方向移动，这样就给了其邻居的机会，实现了种群的多样性。改进之后的互利操作公式为

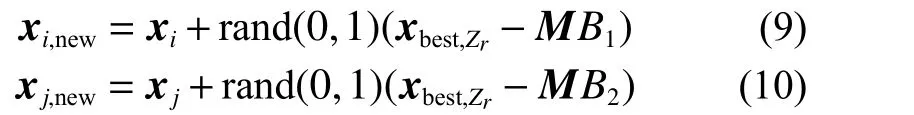
2.4 算法步骤

根据算法思想，HDPS 算法的具体步骤伪代码如下：

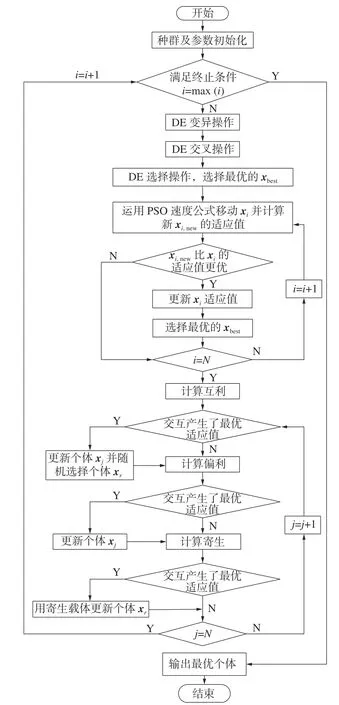
图1 HDPS 算法流程

2.5 时间复杂度分析

HDPS 算法包括了4 个主要部分，除了初始化部分，其他3 个部分都处于循环迭代中，这3 个部分分别对应3 种混合算法的执行过程。因此HDPS 算法的时间复杂度由这3 种混合算法的主要操作决定，这些操作主要包括：差分进化算法变异和交叉、粒子群优化算法速度方程以及共生生物搜索算法交互算子（互利、偏利和寄生）。

设种群的大小为N，每个种群包含了由d维向量组成的个体。通过对算法的分析知道，差分进化算法变异和交叉操作的时间复杂度为O(Nd)，粒子群优化算法中的速度方程和个体适应值判断的时间复杂度为O(Nd)，共生生物搜索算法计算个体适应值和判断新旧适应值更新的时间复杂度也为O(Nd)。所以综上所述，HDPS 算法的时间复杂度为O(Nd)。

3 实验测试

本文对HDPS 算法和当前几个比较著名的混合和非混合的进化算法进行了实验对比测试，测试用例为压力容器设计工程优化问题和减速器设计工程优化问题。实验软件环境为Matlab 2013 和Windows 10 操作系统，硬件环境为Intel Core i7 CPU 2.1 GHZ 和8 GB 内存。在参数设置方面，对于差分进化算法，交叉概率RC=0.7，缩放因子F=0.9；对于粒子群优化算法，c1=c2=2。对于共生生物搜索算法则不需要设置参数。

3.1 压力容器设计工程优化问题

压力容器设计工程优化问题是约束工程优化问题领域的经典案例之一[15]，它的结构包括一个半球形封头盖和一个圆柱体。对这个问题进行优化的目标是最小化生产总成本，包括材料成本、成形成本和焊接成本等。为了控制这些成本，在压力容器的设计过程中，需要选择一些参数，如壳体和封头的厚度（Ts和Th）、内半径（R）和圆柱截面的长度（L），以使其成本最小化。该问题形式化为

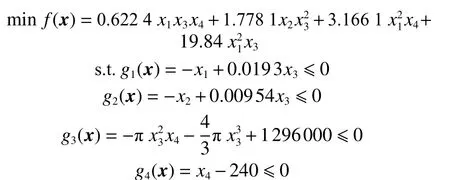
式中：1×0.062 5≤xi≤99×0.062 5 (i= 1, 2)；10≤xi≤200 (i=3, 4)。

针对压力容器设计问题，HDPS 算法与GA3[16]、PSO[3]、CPSO[17]、HPSO[18]、PSO-DE[11]、HCS-LSAL[13]、CMA-ES[19]、TLBO[20]、εDE-LS[21]以及εDE-PCGA[22]等算法进行了实验对比。实验结果如表1 和表2 所示。在表1中，与其他5 种算法相比，HDPS 算法可以达到最优解，也就是达到设计要求的最小值6 059.714 3。在函数评估数和标准差方面，为了达到最优解，HDPS 算法的函数评估次数NFEs=17 320，100 次独立运行的标准偏差为4.36×10-13。由表2 可以看出，与其他算法相比，HDPS 算法在任何方面（函数评估次数NFEs、标准差Sstd等）都是最好的。

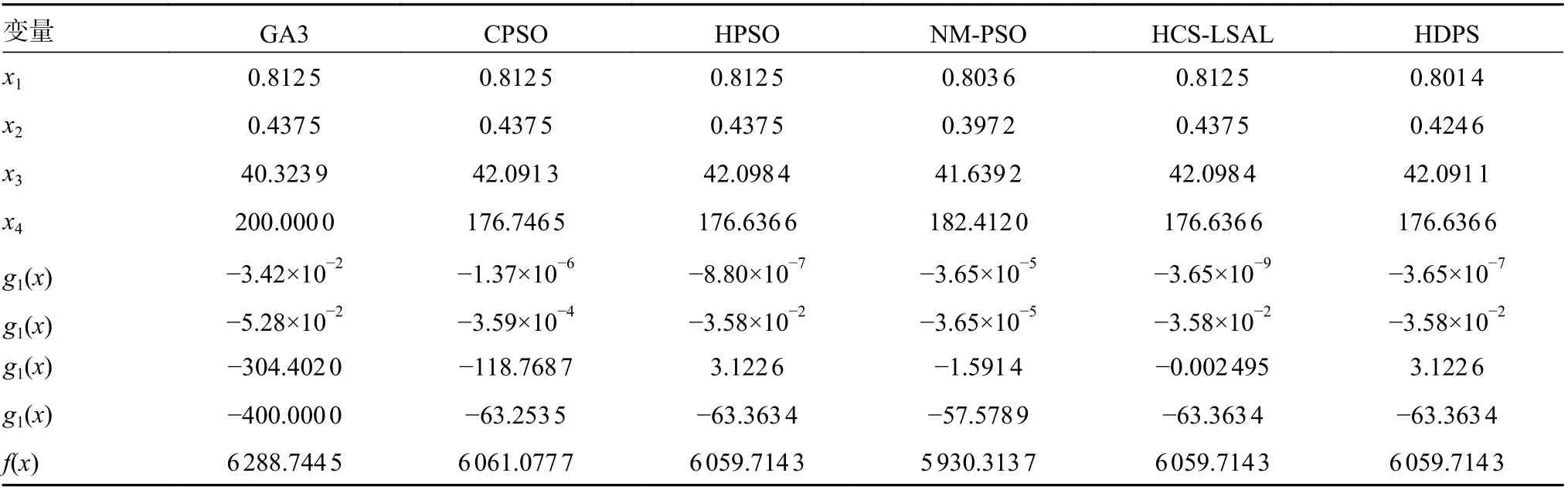
表1 HDPS 算法与其他算法针对压力容器设计问题在最优解方面的比较

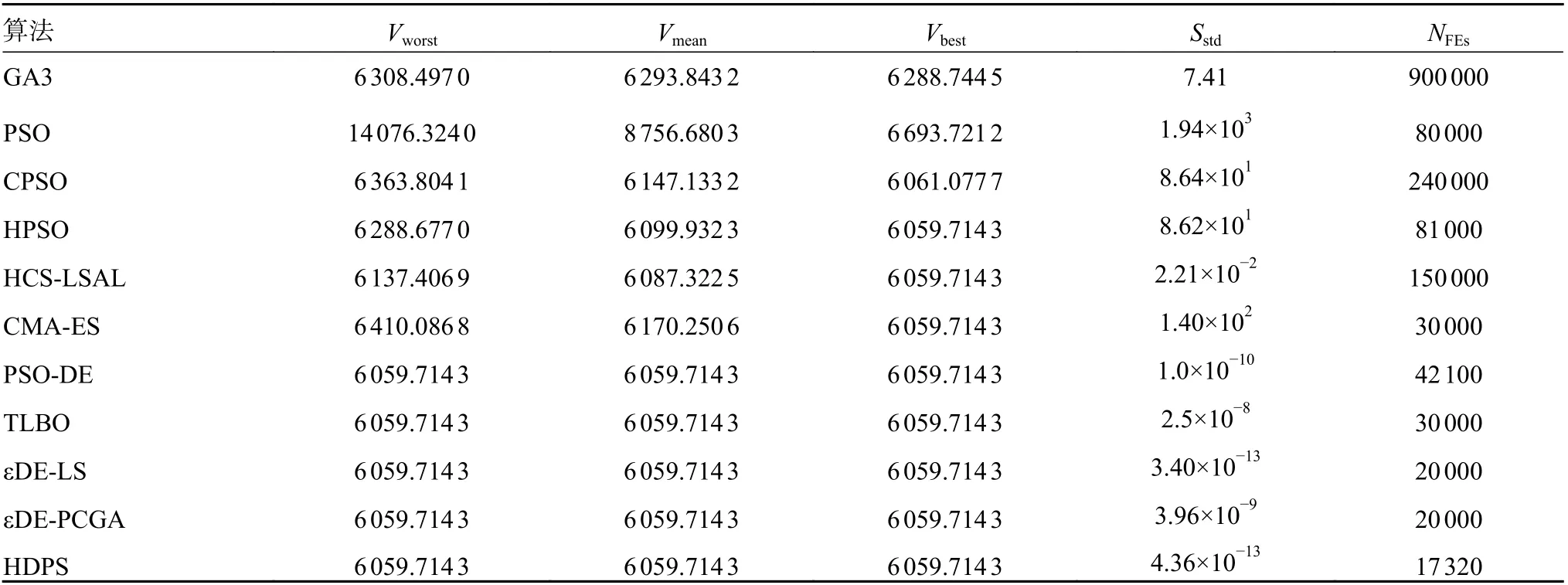
表2 HDPS 算法与其他算法针对压力容器设计问题在函数评估数和标准差方面的比较

3.2 减速器设计工程优化问题

减速器设计工程优化问题是由Golinski[23]提出的另一经典的约束工程优化问题，这个问题的目标是使减速器的重量最小化。从设计结构上看，减速器包含了2 个安装了齿轮的独立轴，这2 个轴通过轴承依次连接到主机架上。减速器设计工程优化问题包含11 个不等式约束，需要通过选择适当的设计参数来控制其重量的最小化：面宽(x1)、齿模(x2)、小齿轮齿数(x3)、轴承间第一轴长度(x4)、轴承间第二轴长度（x5）、第一轴直径（x6）以及第二轴的直径(x7)。

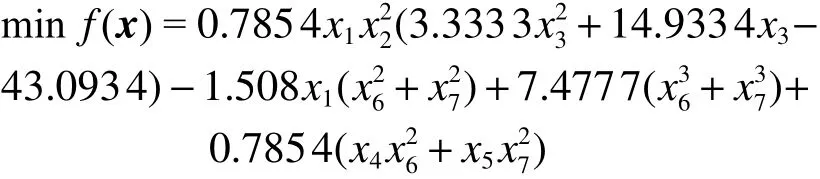
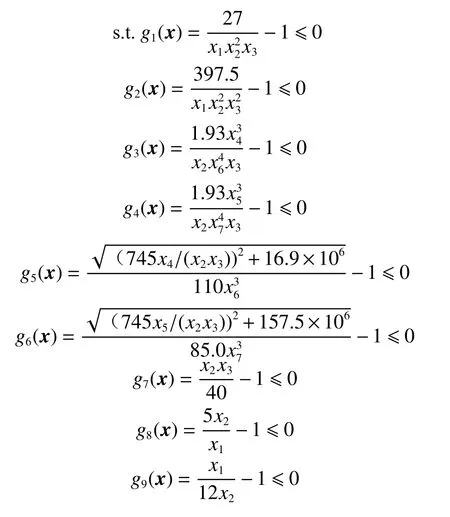
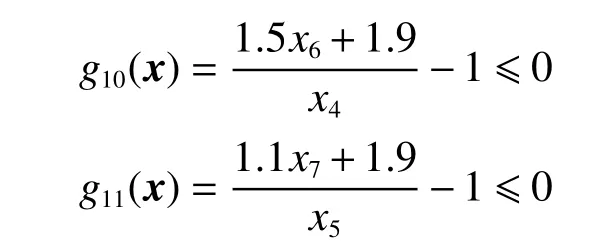
式中：2.6≤x1≤3.6, 0.7≤x2≤0.8, 17≤x3≤28, 7.3≤x4≤8.3, 7.3≤x5≤8.3, 2.9≤x6≤3.9, 5.0≤x7≤5.5。

针对减速器设计工程优化问题，HDPS 算法与DELC[24]，DEDS[25]，HEAA[26]，HCPS[27]，PSGA[10]、CMA-ES[19]、HCS-LSAL[13]、MBA[28]、εDE-LS[21]和εDE-PCGA[22]等算法进行了对比实验，实验结果如表3 和表4 所示。从表3 可以看出，HDPS 算法与HCS-LSAL 算法都达到了设计所要求的最佳值；从表4 可以进一步发现，HDPS 算法的函数评估次数是所有算法中是最低的。

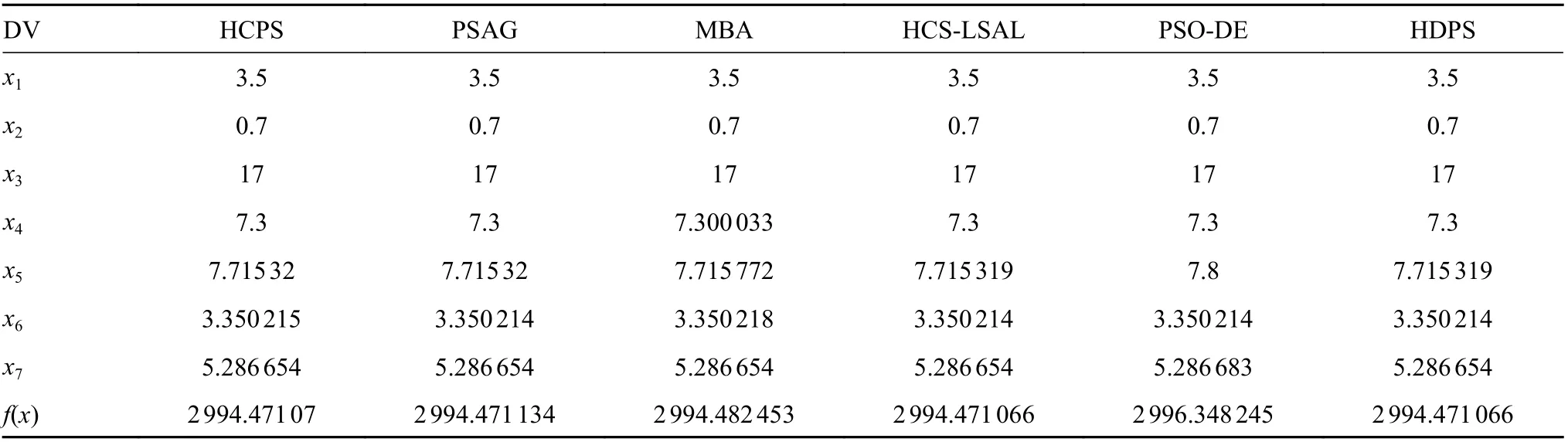
表3 HDPS 算法与其他算法针对减速器设计问题在最优解方面的比较

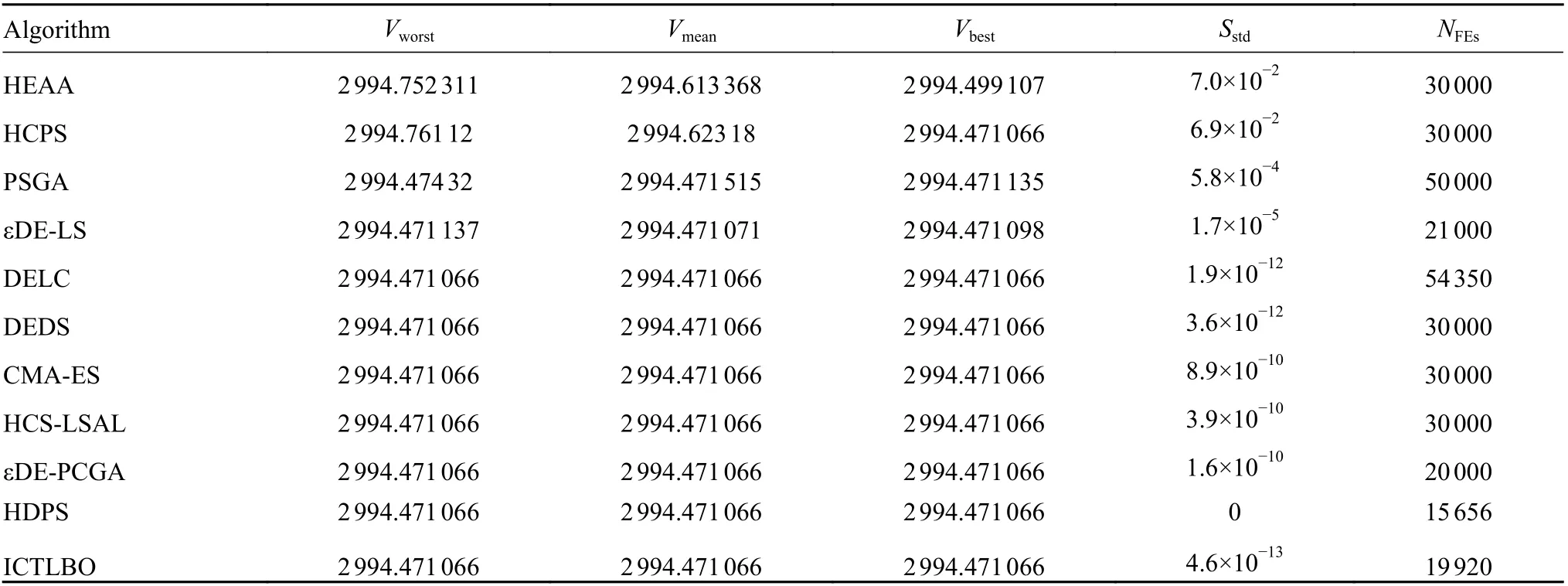
表4 HDPS 算法与其他算法针对减速器设计问题在函数评估数和标准差方面的比较

4 结论

本文基于差分进化算法、粒子群优化算法和共生生物搜索算法，提出了一种求解约束工程优化问题的混合进化算法HDPS。该算法将差分进化算法、粒子群优化算法和共生生物搜索3 种算法操作算子结合起来，对其中的部分算子进行了改进，提高了算法的效率和成功率。例如对共生生物搜索算法互利操作算子进行了改进，使其在一些约束问题上获得了最佳搜索解的效果，这是其他算法所无法实现的。最后将HDPS 算法应用到两类经典的约束工程设计优化问题中进行实验测试，实验结果表明，与混合或非混合的进化算法相比，HDPS 算法不仅提升了问题求解精度，而且大大减少了函数评估的次数。