托卡马克装置中等离子体环向旋转对三维响应场的影响*

李春雨 郝广周† 刘钺强 王炼 刘艺慧子

1) (核工业西南物理研究院,成都 610041)

2) (美国通用原子公司,圣地亚哥 92186-5608)

3) (南华大学核科学技术学院,衡阳 421001)

本文利用MARS-F 程序,数值研究了HL-2M 托卡马克装置高比压等离子体中,环向旋转对外加共振磁扰动场的响应特性的影响.研究发现,等离子体响应显著改变共振磁扰动的谱分布,并影响等离子体内部共振磁扰动场与共振磁扰动线圈电流相位差的依赖关系,从而改变有理面处径向扰动场的幅值.当边界旋转频率较小时,在最外有理面处,等离子体响应对外加共振磁扰动场有明显的放大效应.通常,边缘局域模的控制效果依赖于最外有理面处共振磁扰动场的幅度,因此可通过控制旋转剖面实现对共振磁扰动场的调控,进而优化边缘局域模的控制方案.

1 引言

在托卡马克装置高约束模式放电过程中,通常伴随着一种周期性爆发的边缘磁流体(magnetohydrodynamic,MHD)不稳定性(即:边缘局域模,edge localized mode,ELM[1,2]).当ELM爆发时,会有大量的粒子和热量从等离子体的边缘区域排出到刮削层并最终到达偏滤器.当ELM 足够大时,产生的热负荷可能超过偏滤器材料所能承受的阈值,对偏滤器造成损伤,进而影响整个聚变装置的寿命[3].因此,如何有效控制ELM,降低偏滤器靶板上的热负荷沉积,是目前聚变能研发面临的关键问题之一.

大量的实验和模拟研究表明外加共振磁扰动(resonant magnetic perturbation,RMP)场是控制ELM 的有效方法之一[4-7],但其控制效果对等离子体参数有敏感的依赖性,比如在有限的安全因子窗口内RMP 场才能有效控制ELM[8].同时,控制效果也依赖于RMP 场线圈电流的相位差[9].但迄今,RMP 场控制ELM 的物理解释尚不完整,尤其是在高参数等离子体中,对RMP 场控制ELM的物理机制的认识更为不足,而理解等离子体对RMP 场的响应特性,是研究和理解RMP 场控制ELM 的物理基础.

我国“新一代”托卡马克装置HL-2M 在2020 年实现初始放电.随着装置能力的提升,作为能提供近堆芯条件下等离子体放电实验的平台,HL-2M装置将开展聚变堆相关的关键物理问题研究和技术研发.其中,高参数等离子体中ELM 的控制技术将是一个非常重要的研究内容.目前HL-2M 装置上RMP 线圈的制造已经完成,下一步将安装到装置上.因此,针对HL-2M 未来高参数等离子体放电位形,亟需通过数值模拟方法来研究等离子体对外加RMP 场的响应特性,从而为未来物理实验的开展提供相关物理支持.

在给定平衡的情况下,影响RMP 场在等离子体内部传播和渗透的两个重要物理量是等离子体电阻和旋转[10].前者决定了外加RMP 场能否在等离子体内部传播渗透[11],而后者则主要引起等离子体对外加RMP 场产生屏蔽效应[12,13].当等离子体压强足够大时,等离子体响应对外加RMP 场会有放大作用[14,15],这种放大作用可能会影响RMP场控制ELM 的效果.本文基于HL-2M 托卡马克装置未来可能的放电位形,数值研究了高比压等离子体对RMP 场的响应特性,并深入研究了等离子体旋转剖面对等离子体响应的影响.

本文在第2 部分介绍所采用的基本物理模型和模拟程序,在第3 部分展示了数值结果,并在第4 部分给出了结论和讨论.

2 MARS-F 物理模型和共振磁扰动线圈布置

2.1 MARS-F 计算模型

使用MARS-F[16]代码来计算等离子体对外部RMP 场的响应.此代码是基于环几何位形,并采用电阻性单磁流体模型的线性程序.MARS-F 同时包含了等离子体流速V0的径向分布,其中R是等离子体大半径,Ω是环向旋转角频率,这里Ω是等离子体小半径的函数,是几何环向角φ的单位矢量.

MARS-F 求解包含了线性等离子体响应的电阻性MHD 方程组:

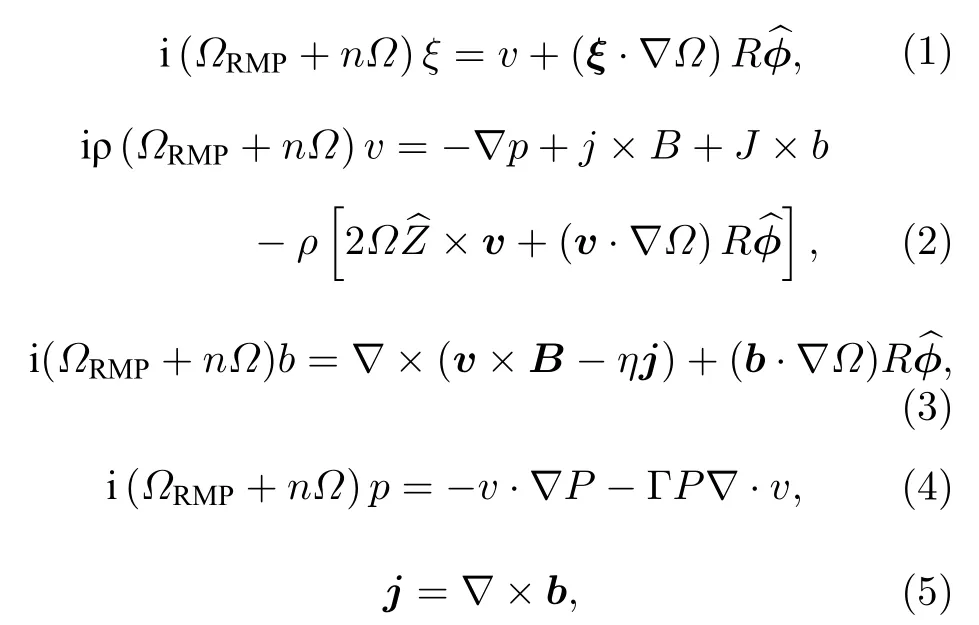
其中变量ξ,v,p,j和b分别表示等离子体位移,扰动速度,扰动压强,扰动电流和扰动磁场.等离子体密度,磁场,压力和电流的平衡量分别用ρ,B,P和J表示,n为环向模数.求解过程中,方程进行无量纲化处理,长度由磁轴的大半径归一化,时间由环向阿尔芬时间τAR/vA归一化,vA是阿尔芬速度,环向旋转频率Ω由阿尔芬频率ΩA1/τA归一化,磁场和压强则分别由磁轴处场强为B0和归一化.外加三维场是由设置在真空区域的RMP 线圈上的电流所产生.在MARS-F 代码中,RMP 线圈电流jRMP被设定为源项,满足安培定律∇×bjRMP.电流源的频率由方程(1)—方程(4)中的ΩRMP表示,本文考虑的是外加静态RMP场的情况,即:ΩRMP0 .将上述方程在磁面坐标系中求解,并选择环向角作为几何角度,而小半径则由归一化极向磁通表示.

2.2 共振磁扰动线圈配置

目前,HL-2M 上设计的两组RMP 线圈位于装置的弱场侧,分别位于中平面的上侧和下侧位置,可以简称为上线圈和下线圈,如图1 所示.由于每组在环向上有8 个线圈,因此可以产生主要环向模数为n1,2和4 的磁场扰动.在实验中,可以通过改变上下两组线圈中电流的大小和方向来对RMP 场的空间分布及其强度进行调整.由于本文主要研究等离子体线性响应,在给定RMP 线圈电流相位差和等离子体参数的条件下,响应场的幅度与RMP 线圈安匝数成正比,所以我们之后展示的结果均为RMP 线圈每千安匝产生的RMP 场的强度(即:G/kAt).

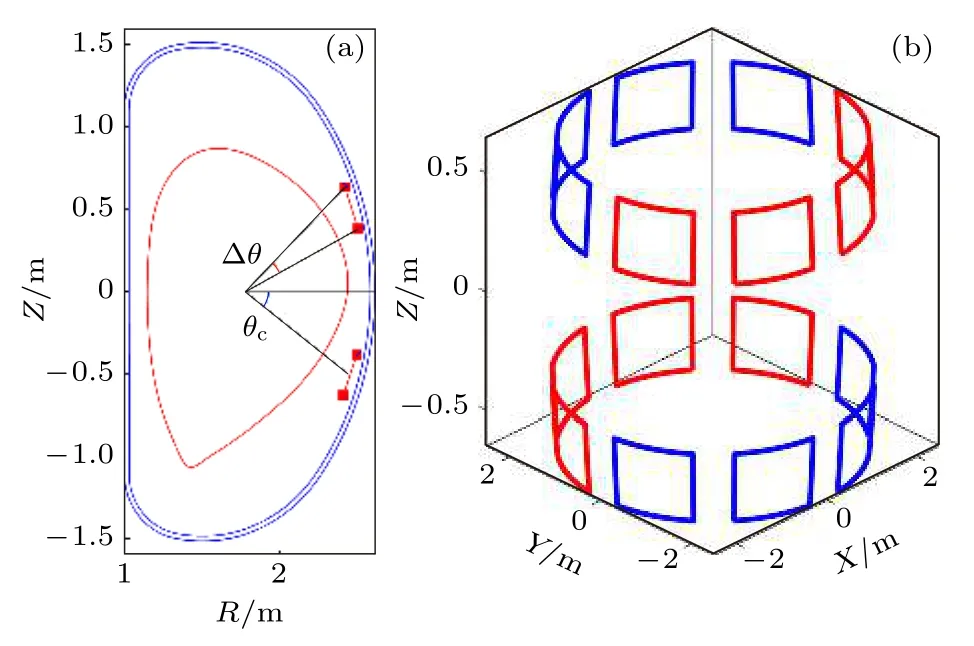
图1 (a) HL-2M 装置真空室壁(蓝色)和等离子体边界(红色)极向截面示意图,以及RMP 线圈极向位置(红色方块);(b) RMP 线圈的三维几何位形,图中方框的红色和蓝色示意RMP 线圈不同的电流方向,这里展示的是环向模数n=1,相位差为180°的示意图Fig.1.(a) Wall shapes (blue lines) of HL-2M,plasma boundary (red line) and the poloidal location of RMP coils(red squares);(b) geometry of the RMP coils.Red and blue colors indicate the different directions of RMP current flow.(b) shows a n=1 case with a toroidal phase difference Δφ=180°.

HL-2M 装置上RMP 线圈的几何参数(极向位置θc±36°,极向宽度 Δθ17°,环向宽度 36°)已设计完成[17],如图1 所示,每个线圈电流上限为10 kAt.在未来HL-2M 的实验中,需要根据不同的放电条件优化上下两组线圈电流之间的相位差,Δφφupper-φlower.图1(b)中展示了环向模数n1,相位差为 Δφ180°(奇对称)的RMP 线圈配置情况示意图.

2.3 HL-2M 的平衡参数

本文重点研究高比压放电条件下,环向旋转对等离子体响应的影响,因此这里选择了归一化比压βN2.8的平衡,其略低于对应的无壁比压极限3.2.图2 展示了平衡压强、密度、旋转频率和安全因子q的径向分布剖面.图2(c)展示两种环向旋转频率剖面,分别标记为p1和p2,二者形状相同但在等离子体边界处的旋转频率分别为-3×10-4(p1)和 3×10-4(p2).在实际放电过程中,由于存在新经典阻尼力矩,湍流产生的雷诺协强,自发旋转以及离子损失等因素,等离子体环向旋转在边界的剖面演化过程往往较为复杂.边界区域Ω可能为正,也可能为负.因此为了模拟实验上不同的放电条件,这里选取了边界Ω分别为正值和负值的两种情况.需要指出的是,对于p1 剖面而言,在等离子体内部存在旋转频率为零的情况,在该位置处等离子体对外加RMP 场的屏蔽作用非常弱,此处RMP 场的强度主要由电阻性磁扩散决定[18].在图2(d)中,磁轴和边界处的安全因子分别为q01.87和qa10.2,95%归一化极向磁通位置处的安全因子为q959.88,安全因子最小值为qmin1.32.对于本文研究的n1 的RMP 场而言,等离子体内部将有9 个有理面,从m2到m10,m为极向模数.

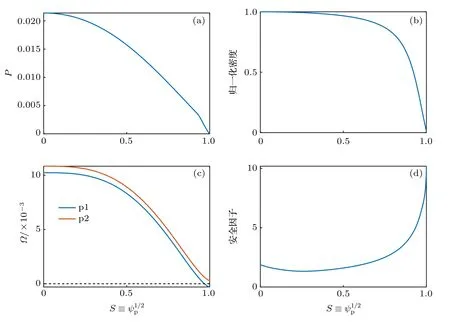
图2 HL-2M 上等离子体平衡的径向剖面 (a) 由/μ0 归一化的压强剖面;(b) 归一化的密度剖面;(c) 由磁轴处阿尔芬频率归一化的旋转频率剖面‘p1’和‘p2’;(d)安全因子剖面Fig.2.The radial profiles of the HL-2M plasma equilibrium used in this study:(a) The plasma equilibrium pressure normalized by/μ0;(b) the normalized plasma density;(c) the plasma toroidal rotation,normalized by the Alfven frequency at the magnetic axis;(d) the safety factor profile.

上述平衡其他的参数包括,B02.2 T,大半径R1.78 m,小半径a0.65 m,电流Ip0.85 MA,磁轴处电子密度为n04.7×1019m-3,对应的阿尔芬时间τA3.6×10-5s .为了简单起见,在以下的计算过程中,我们假设电阻为常数,并且选取伦德奎斯特数(Lundquist number)S107.S值对应的是q10 有理面上等离子体Spitzer 电阻的大小.另外,我们也验证了结论和电阻模型的依赖性,发现即使采用Spitzer 电阻模型(即:考虑电阻和温度的依赖关系),不会改变本文的结论.

3 数值模拟结果

3.1 RMP 线圈电流相位优化的判据

径向RMP 扰动场的傅里叶分量在磁面坐标系下可表示为

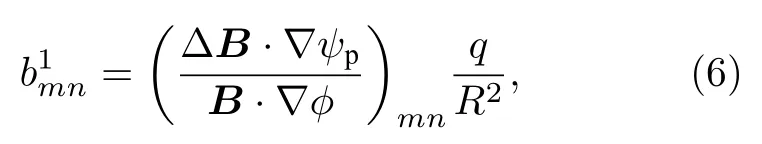
其中ψp为极向磁通,ΔB为RMP扰动场,q和R为安全因子和大半径,m为极向模数.本文m的取值范围为[—50,50],n设置为1.

在进行RMP 线圈配置参数优化时,经常用到两个判据,一个是最外侧有理面处的m/n10/1) (也表示为)的幅度,另一个是选用X点附近的法向扰动位移(ξx)或ξx与中平面处扰动位移的比值.和有理面上产生的磁岛有关,通常共振径向扰动场会在相应的有理面上产生磁岛,而磁岛宽度的平方与共振磁扰动的幅度成正比.当有理面处的径向扰动磁场幅度足够大,磁岛足够宽且相邻有理面比较接近时,会导致磁岛在径向上的重叠,同时增强等离子体的径向输运,降低台基区的压强梯度,进而降低对ELM 的驱动,实现对ELM 的控制[19,20].考虑到实验过程中扰动量的易探测性,ξx也可作为RMP 线圈配置优化的判据,并且ξx可用高速CCD 相机观测[21].大量的模拟结果也证实这两种判据预测的结果基本一致[22,23].正如前面所述,HL-2M 装置RMP 线圈的几何参数,安装位置已经确定,需要优化的RMP 线圈配置参数主要是指上下两组RMP 线圈的相位差 Δφ.

3.2 模拟结果分析

图3 真空和包含等离子体响应的最后一个有理面处径向扰动场共振分量()随上下组线圈(环向模数n=1)电流相位差 Δφ 的变化Fig.3.The resonant radial field amplitude () at the last rational surface of the vacuum RMP field and the total RMP field including the resistive plasma response,while scanning the coil phasing Δφfor the n=1 configuration.

为了进一步理解高比压等离子体中环向旋转对等离子体响应场的影响,分析了不同情况下径向RMP 场的傅里叶分量在小半径方向的分布情况,如图4 所示.这里选取了p1 旋转剖面对应的最优和最差相位差.图4(a)表明等离子体响应能显著改变RMP 场傅里叶分量的径向分布,在芯部有理面位置处(竖直虚线所示),等离子体响应主要起到屏蔽作用;而在偏离有理面的某些位置上,等离子体响应对外加RMP 场有放大作用,且这种放大作用与等离子体旋转剖面有关,但其物理机制还需进一步的研究.本文更为关注等离子体响应对最外有理面处共振扰动场(qm/n10/1)的影响.图4(b)表明,选取 Δφbest-130°时,p1旋转剖面对应的幅度远大于真空情况下以及p2 旋转剖面下的幅值.这进一步说明在给定相位差的情况下,高比压等离子体中对旋转频率剖面有非常强的依赖关系.当选取 Δφworst50°时,图4(c)和(d)也同样表明径向RMP 场的分布以及依赖于等离子旋转频率剖面.

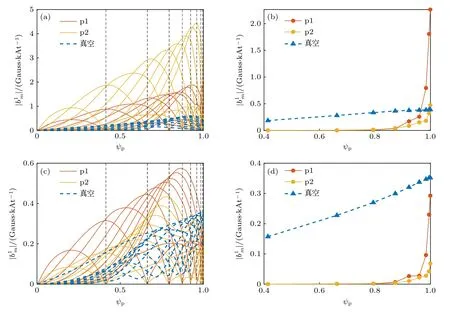
图4 (a),(b) 在最优相位差 Δφbest=-130°情况下,真空RMP(n=1)场和总的RMP 场(考虑了等离子体响应场)共振分量径向分布的对比;(c),(d)对应选取最差相位 Δφworst=50° 的对比.(a)和(c)展示的是共振傅里叶分量的径向分布对比,(b)和(d)展示的是有理面处相应共振分量的对比.p1和p2 分别表示不同的旋转速度剖面(图2(c)所示)Fig.4.Comparison of the n=1 vacuum RMP field and the total field perturbation including the plasma response,for the resonant radial field components assuming:(a),(b) The coil phasing Δφbest=-130°;(c),(d) the coil phasing Δφworst=50° .Shown in left panels are radial profiles of all resonant poloidal harmonics and in right panels the resonant field amplitude at the corresponding rational surfaces indicated by the vertical dashed lines in Figure (a) and Figure (c).p1 and p2 denote the adopted different rotation profiles as shown in Fig.2(c).

图5 对比了三种情况下,径向RMP 扰动场不同m的傅里叶分量(如,这里n1)沿着径向分布的最大值(max).结果表明,等离子响应不仅对共振分量(m2,3,···,10)的 max有明显的放大作用,而且对非共振分量10＜m＜30的max也有很强的放大作用,后者的物理成因主要是由于环形几何效应导致的非共振分量与共振分量之间的耦合所导致.对于-20＜m＜0 的非共振分量 max,等离子体响应对外加真空RMP场只有较弱的放大作用,而对于其他分量的 max,等离子体响应所带来的贡献比较小.

图5 真空径向场和总径向场的不同极向模数傅里叶谐波沿径向的最大振幅比较,实心为 m=2,3,···,10,的共振谐波,空心为非共振谐波.p1和p2 分别表示不同的旋转速度剖面(图2(c)所示).这里选取了最优相位Δφbest=-130°Fig.5.Comparison of the maximal amplitude (along the minor radius) of the poloidal Fourier harmonics of the radial magnetic field for the vacuum and total RMP.Solid and hollow markers denote the resonant (i.e.m=2,3,···,10)and non-resonant harmonics,respectively.p1 and p2 denote the adopted different rotation profiles as shown in Fig.2(c).Δφbest=-130° is used here.

图6 展示了p1 剖面,p2 剖面以及真空三种情况下,RMP 扰动场在()空间的谱分布.图6(a)、6(b)、6(d)和6(e)表明等离子体响应导致芯部区域有理面处径向RMP 扰动场显著降低,这主要是由于等离子体对外加场的屏蔽效应所导致.另外,图6(a)、6(d)和6(b)、6(e)表明虽然旋转频率剖面的不同会导致RMP 场的幅度不同,但是RMP 场的谱分布相似.在 Δφ-130°时,RMP场的谱非对称分布(相对m=0 而言),与图6(c)所示的真空情况的结果对比可知,上述非对称性分布是由等离子体响应引起的;在 Δφ50°时,两种旋转频率剖面下的RMP 场的非共振分量(即,-50＜m＜-10与 10＜m＜50)基本上成对称性分布.图6(c)和图6(f)也表明,真空RMP 场谱分布的对称性和相位差 Δφ有一定的依赖关系,如相位差为 Δφ-30°时,RMP 场谱分布的对称性更为明显.而在某些特殊电流相位下,如 Δφ0°或180°时,真空的RMP 场谱分布会变成相对m0严格对称[12].

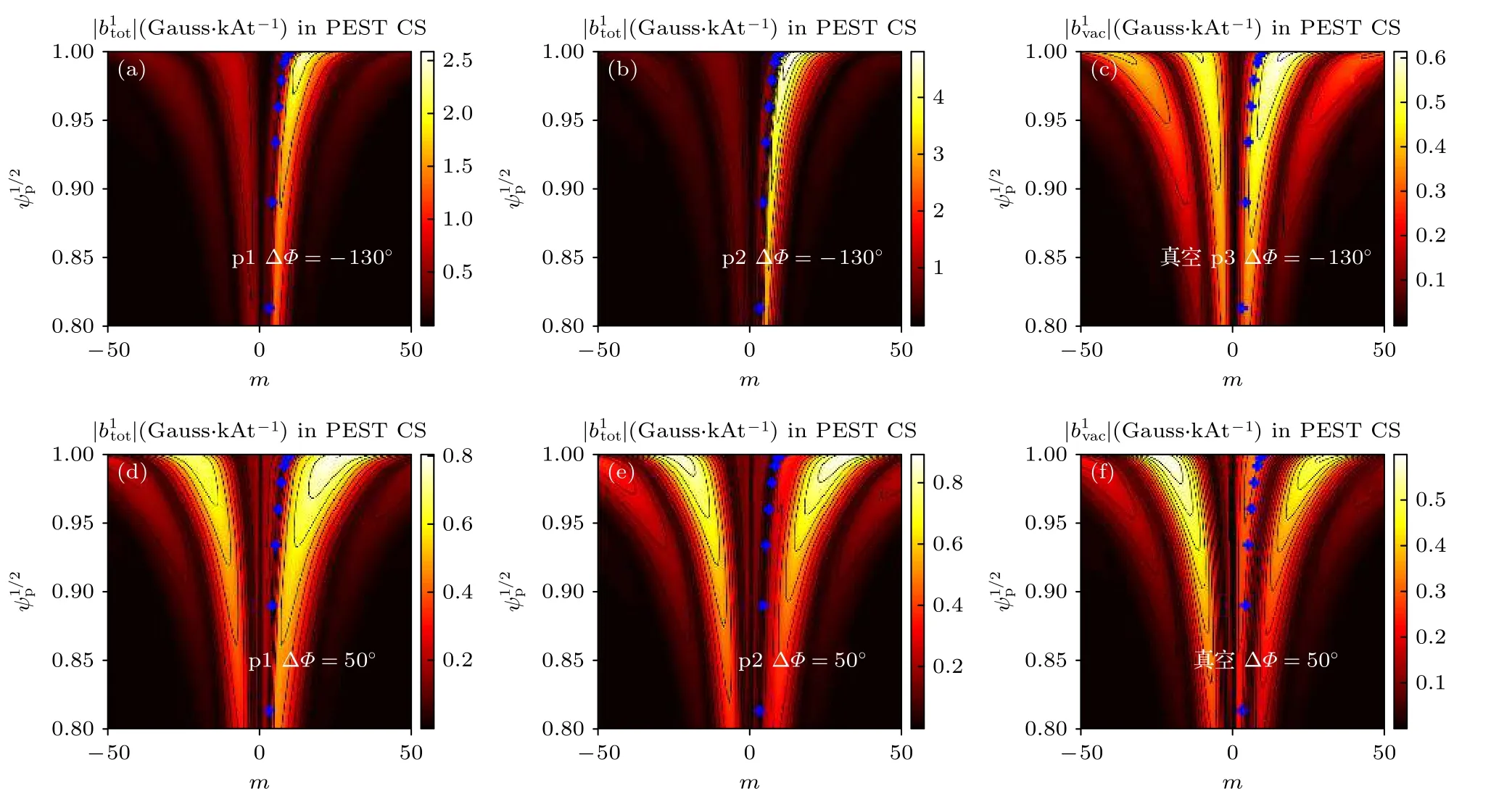
图6 展示了包含(a),(b),(d),(e)和不包含等离子体响应(c),(f)情况时 n=1RMP 场在模数(m)和极向磁通()二维空间上谱的分布情况.(a)—(c) 选取了相位 Δφ=-130°,(d)—(f) 选取了相位 Δφ=50° .p1和p2 分别表示不同的旋转速度剖面(图2(c)所示)Fig.6.Computed poloidal spectra of the n=1 RMP for the total response radial field including the plasma response (a),(b),(d),(e) and that of the vacuum radial field alone (c),(f),plotted along the poloidal harmonic number m and the plasma radial coordinate.Assumed in Figure (a)—(c) is the coil phasing Δφ=-130° .And in Figure (d)—(f) the coil phasing Δφ=50° .p1 and p2 denote the adopted different rotation profiles as shown in Fig.2(c).

为了进一步研究旋转频率剖面对RMP 场的影响,在不改变旋转频率梯度的情况下,整体改变旋转频率Ω的幅度.如图7(a)所示,等离子体边界处的归一化旋转频率从-1×10-3变化至 9×10-4.在改变Ω的过程中,可能使得等离子体某个有理面处的旋转频率接近零.此时,等离子体旋转所导致的对外部RMP 场的屏蔽效应将显著降低,从而使该位置处的RMP 场强度增加.并通过环形几何效应导致的极向分量之间的耦合进一步影响相邻有理面处RMP 场的分布和强度,使得RMP 场控制ELM 的效果与边缘区域等离子体旋转频率的剖面密切相关.图7(b)表明旋转频率剖面几乎不影响最后一个有理面处RMP 共振场两个极值所对应的最优和最差相位差,但是其幅度与旋转频率剖面有敏感的依赖关系.

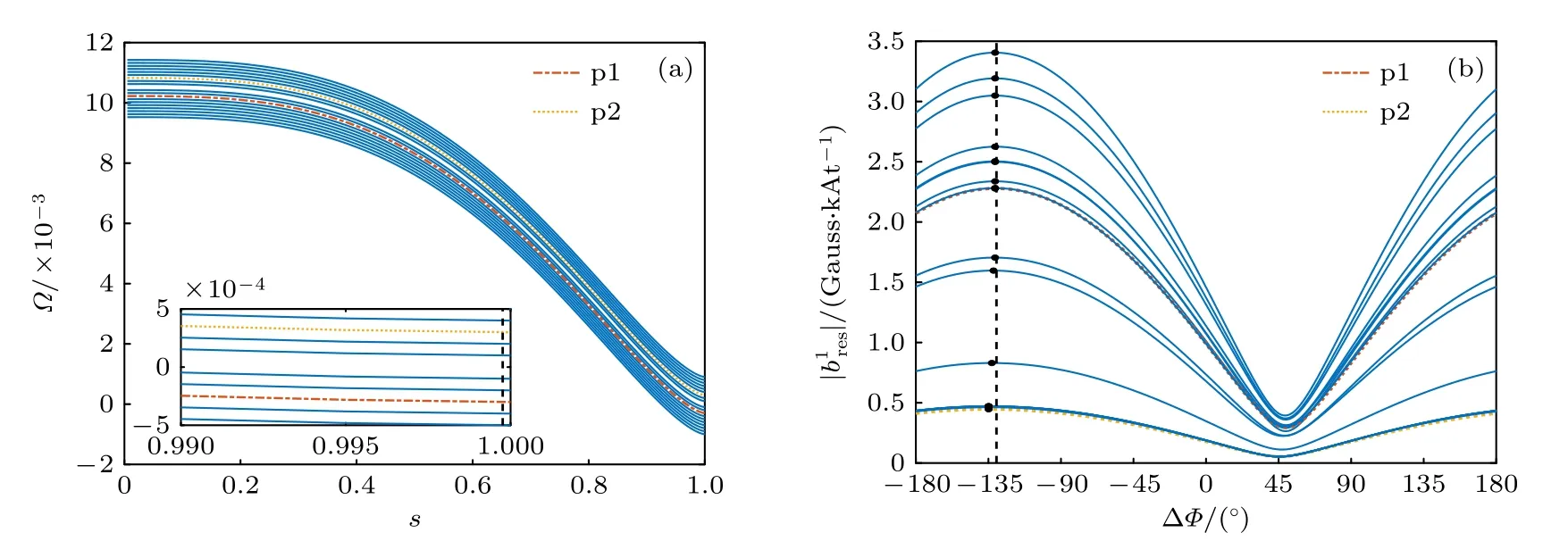
图7 (a) 选取的不同旋转速度剖面;(b) 不同旋转速度剖面情况下,最后一个有理面处共振径向扰动场()和 n=1 RMP 线圈电流相位差 Δφ 的依赖关系.p1和p2 对应于图2(c)所展示了两种旋转速度剖面.(b)中垂直虚线为p1 对应的最优相位差,实心点标记不同旋转剖面分别对应的最优相位差Fig.7.(a) The chosen various rotation profiles;(b) the resonant radial field amplitude () at the last rational surface of the total RMP field as scanning the coil phasing Δφfor the n=1 configuration,for choosing different rotation profiles given in Figure (a).p1 and p2 denote the rotation profiles shown in Fig.2(c).Vertical line denotes the best coil phasing for the p1 case,while the solid dots label the corresponding best coil phasing for the different rotation profiles.

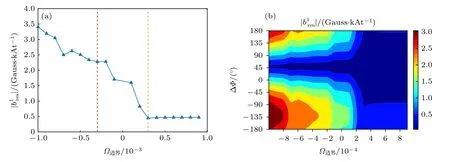
图8 (a) 最后一个有理面处共振径向扰动场()和边界处等离子体环向旋转之间的依赖关系.这里选取了 Δφ=-130° ;(b)展示了(Δφ,Ω边界)二维参数空间上的分布情况Fig.8.(a) The resonant radial field amplitude () at the last rational surface of the total RMP field as varying the plasma toroidal rotation at edge (as shown in Fig.7).Δφ=-130°is used;(b) contour plot of on the 2-D plane of (Δφ,Ω边界).

4 总结与讨论

本文数值研究了HL-2M 高比压(βN～2.8)等离子体中,不同旋转剖面情况下,等离子体对外加共振磁扰动(RMP)场的响应特性.研究发现,与真空情况相比,等离子体响应能显著改变RMP 场的谱分布与RMP 线圈电流相位差的依赖关系,并改变有理面处径向扰动场的幅值.等离子体响应将真空条件下的最优相位 Δφbest150°和最差相 位 Δφworst-30°分别改变为Δφbest-130°和Δφworst50°.这里我们将位于最后一个有理面(即qm/n10/1)处的径向RMP 场的共振分量最大值和最小值所对应的相位差标示为最优相位 Δφbest和最差相位 Δφworst.考虑等离子体响应后,所能达到的最大值与等离子体边缘处的旋转频率分布密切相关,当边缘旋转频率小于一定的阈值或反向时,显著增强.其物理机制为:在改变旋转频率的过程中,使等离子体边缘区域某个有理面处的旋转频率接近零,这时等离子体旋转所导致的对外部RMP 场的屏蔽效应将显著降低,进而导致此处的RMP 场强度增加,并进一步通过极向分量之间的耦合效应影响相邻有理面处径向RMP场的分布和强度.另外,也发现低比压(βN～1)情况下,在边界旋转速度小于零时,等离子体响应对也有放大效应,但其比高比压时的放大效应要弱.这表明适当的调控边缘区域等离子体旋转频率剖面,有利于增强最后一个磁面处的幅度,进而在控制ELM 过程中降低对RMP 线圈电流的需求.实验上可通过调整不同注入方向中性束的功率实现对边界等离子体旋转速度和方向的调制.下一步将在更宽的比压,等离子体位形参数范围内,研究不同旋转频率剖面对RMP 场特性的影响,为未来HL-2M 高参数等离子体放电过程中ELM 的控制提供更为系统的模拟支持.