连续离散时间模型的传播速度和行波解
2022-04-15王明龙
王明龙,李 状
(西南大学 数学与统计学院, 重庆 400715)
生物种群的繁殖、死亡和扩散如何影响其持久性和传播速度是空间生态学的重要研究内容[1-2],数学模型在空间生态学理论[3-6]和此类问题研究中发挥了重要作用。其中一类传统的研究空间种群动力学行为的模型是反应扩散方程模型,该类模型假设种群的成长和扩散是同时发生的。然而,许多物种的繁殖和扩散发生在一年中的不同季节,例如哺乳动物和水生物种等,此时经典的反应扩散方程并不适合用来描述种群的持久性和空间传播的性质。
1 模型建立
Lewis等[7]建立了具有不同繁殖和扩散的脉冲反应扩散模型,并研究了模型的传播速度、行波解和临界区域尺寸。模型表达式见式(1)。
(1)
模型(1)的非扩散阶段由离散映射g描述,映射g综合了种群的繁殖和生长过程。考虑到许多物种的生命周期包含多个成长阶段,本研究对文献[7]建立的模型进行延伸,建立多阶段的脉冲反应-扩散模型,见式(2)。
(2)
以湖泊中贝壳类生物为例。这类生物由成年个体释放生殖细胞,生殖细胞在水中扩散,然后沉降下来与卵细胞结合形成受精卵后成长为幼年个体,最后生长为有繁殖能力的成年个体。这里,un(x,t)表示第n年、时间为t、位置在x的生殖细胞密度;wn(x,t)表示沉降下来的生殖细胞密度;J(x,n)和A(x,n)分别表示幼年阶段和成年阶段的种群密度;扩散系数d>0,为常数;m表示扩散过程中生殖细胞的死亡率;σ表示扩散过程中沉降率;s1表示生长到幼年阶段的概率;s2和s4分别表示幼年和成年个体存活到本阶段下一年的概率;s3表示幼年个体生长到成年阶段的概率;f表示脉冲出生函数。这类模型也可用来描述植物种群的扩散生长过程。
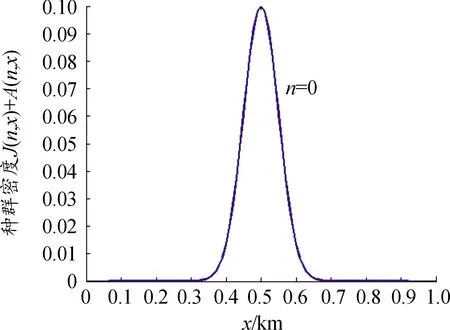
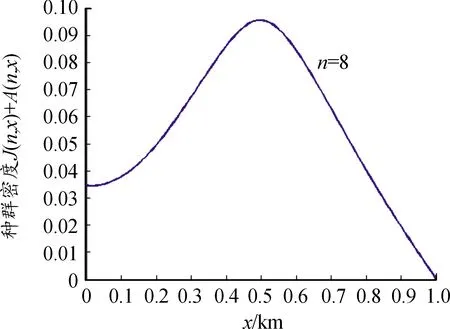
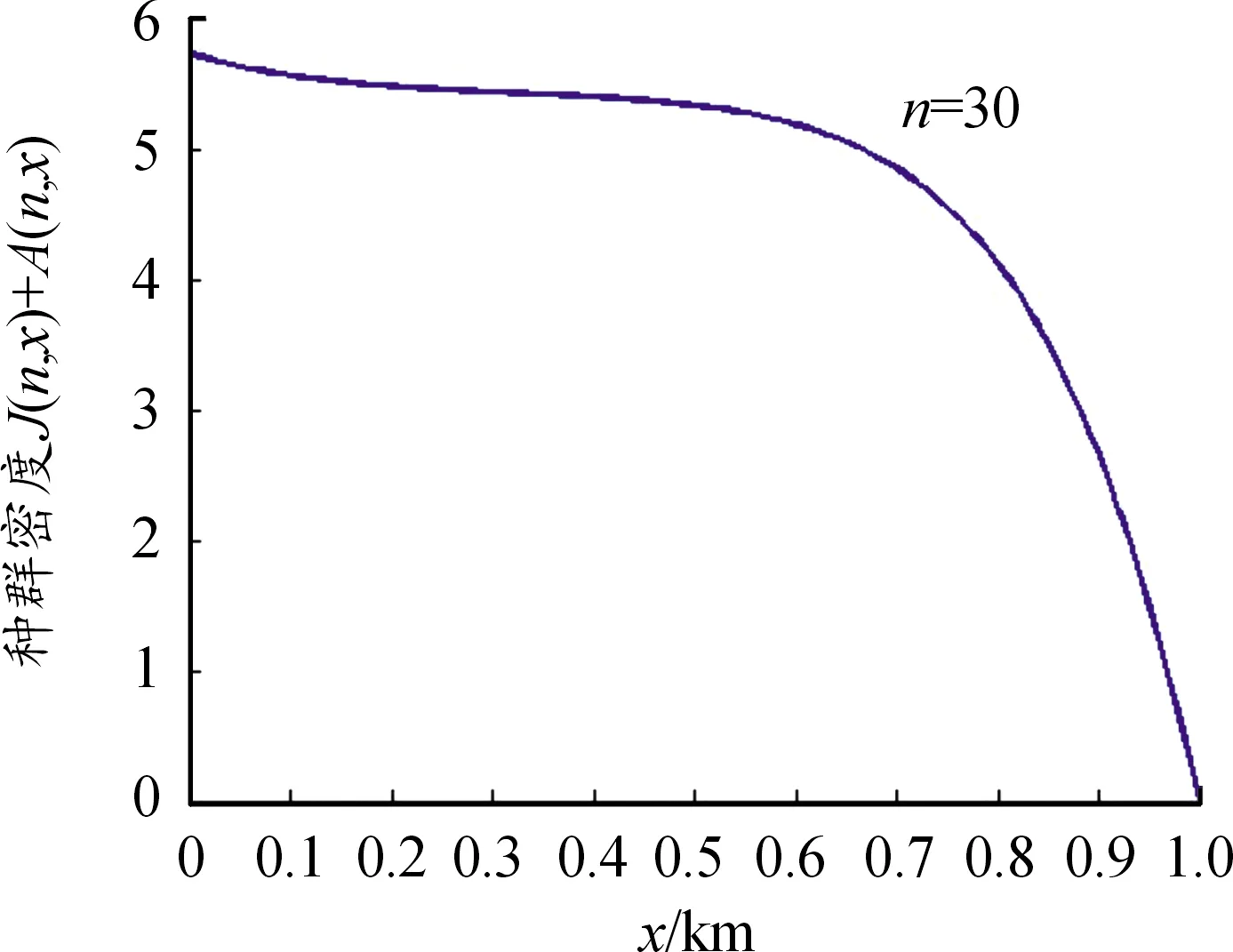
假设1(i)m和σ是正数,0 (iii)存在正常数r,R,使得对于0≤A≤r,f(A)≥f′(0)A-RA2。 若种群没有扩散,即d=0,则模型(2)退化为 (3) (4) 模型(4)有平凡解0。考虑方程的正常数平衡解,将式(4)的第2个方程代入第1个方程得到 (5) (6) 满足给定的初值条件: u(x,0)=δ(x),w(x,0)=0 这里δ(x)是Dirac函数。令k(x)=w(x,T),对系统(6)的第2个方程两边关于t∈[0,T]进行积分得: 再对系统(6)的第1个方程两边关于t∈[0,T]进行积分: (7) u(x,T)表示扩散结束时个体的密度。个体一边扩散一边沉降,此时的u(x,T)是非常小的,可近似看作0,方程(7)变为 (8) (9) 通过在式(9)中等号右边用x-y替换x来定义k(x,y)。根据分布核的定义,降落的个体为: 代入到式(2)第3个方程,模型(2)变为积分差分方程 (10) 定义算子Q为 (11) 这里N=(J,A)T。算子Q在0处线性化为 (12) 引入对应线性算子的矩母矩阵Bμ满足:对每个常数向量α,有Bμα=L[αexp(-μx)]|x=0,因此 这里 (13) 将式(13)第2个方程代入第1个, (14) 令 (15) 引理1若假设1成立,则Bμ的主特征值λ(μ)是严格对数凸的。 证明文献[9]的引理6.4表明,λ(μ)是对数凸的,即:对于0 λ(tμ1+(1-t)μ2)≤λt(μ1)λ1-t(μ2) (16) 反证。若式(16)中的等号成立,则式(14)可写成 (17) 由于K(μ)满足K(μ)K″(μ)>(K(μ))2,所以K(μ)是严格对数凸函数,即 K(tμ1+(1-t)μ2) 对式(17)应用赫尔德不等式得 (18) 由式(14)可知式(18)的第1式1<1,矛盾。所以λ(μ)是严格对数凸的。 定义传播速度 (19) 这里 定理1若假设1成立,则式(19)定义的系统(2)的传播速度c*具有下列意义: 若连续初值函数N0(x)在有界区域外是0,但是N0(x)不恒为0,并且0≤N0(x)<β,则对于任意的ε>0,系统(2)的解Nn(x)具有下列性质: 定义算子 Q(j)[N](x)=Q[η(·/j)N(x+·)](0) 定义Q(j)的传播速度为 这里 又Φ(j)关于j非减,若k≥j,则 系统(2)有波速为c的行波解满足w(x-c)=Q[w](x),等价于 定理2若系统(2)满足假设1中的条件,则下列结论成立: 1) 若c>c*,系统(2)存在连续非增的行波解w(x-nc),满足w(-∞)=β,w(+∞)=0。 2) 若c 定义 w+(x)=min{exp(-μcx)ξ(μc),β} w-(x)=max{τ[exp(-μcx)ξ(μc)-exp(-μτx)ξ(μτ)],0} 其中,w+(x)是非增函数。令z0(x)=w+(x),由zn+1(x)=Q[zn](x+c)构造序列{zn(x)}: z1(x)=Q[exp(-μcx)ξ(μc)](x+c)≤L[exp(-μcx)ξ(μc)](x+c)= Q具有保序性,根据递推得 zn+1(x)≤zn(x)≤w+(x) 文献[11]中定理5的证明表明,对于充分小的τ,通过假设(iii)和序列递推,得到 w-(x)≤zn+1(x)≤zn(x)≤w+(x) 下面证明结论(2)。反证,假设对于c vn(x)≤w(x-nc) (20) 对模型(2)的解进行数值模拟,研究解的动力学行为。选取出生函数f为Beverton-Hold函数。 这里f(A)是非减函数。 图1表示初始时的种群分布情况,图2表示第8年种群分布情况,图3为达到稳定状态的种群分布情况。不同年份的种群分布情况描述了种群持久性。 图1 初始时的种群分布情况 图2 第8年种群分布情况 图3 达到稳定状态的种群分布情况 研究了具有阶段结构的脉冲反应扩散种群模型,在正常数平衡解存在的前提下,根据模型中的扩散和降落,得到在无界区域的扩散核。这种扩散核能把模型转换为积分差分方程来研究模型的传播速度和行波解。本文中出生函数是单调非减的,下一步将对出生函数为非单调的情况进行研究。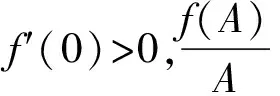
2 正常数平衡解
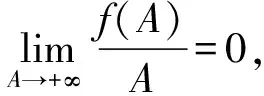
3 传播速度



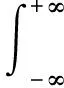
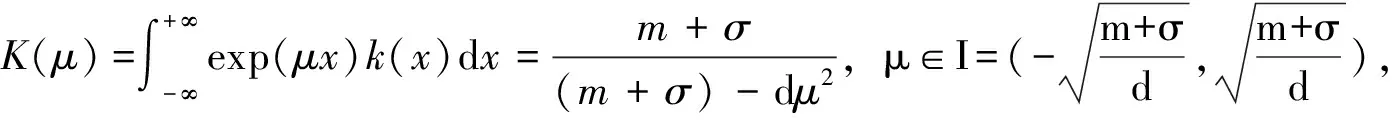
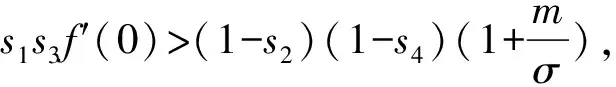
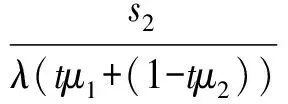
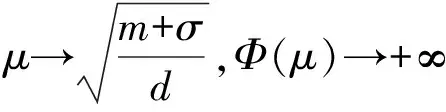
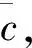
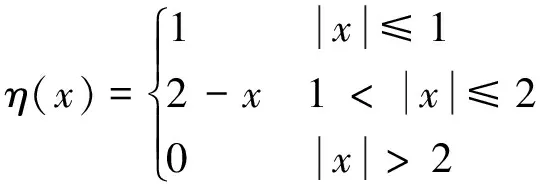

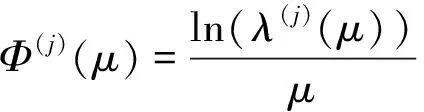
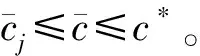
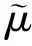
4 行波解
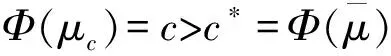
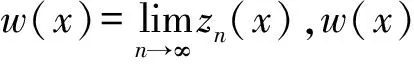
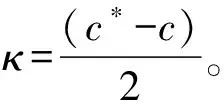
5 数值模拟
6 结论
