Distributed Periodic Event-Triggered Optimal Control of DC Microgrids Based on Virtual Incremental Cost

Jiangkai Peng,, Bo Fan,, Zhenghong Tu, Graduate Student,Wei Zhang, Senior, and Wenxin Liu, Senior

Abstract—This article presents a distributed periodic eventtriggered (PET) optimal control scheme to achieve generation cost minimization and average bus voltage regulation in DC microgrids. In order to accommodate the generation constraints of the distributed generators (DGs), a virtual incremental cost is firstly designed, based on which an optimality condition is derived to facilitate the control design. To meet the discrete-time (DT)nature of modern control systems, the optimal controller is directly developed in the DT domain. Afterward, to reduce the communication requirement among the controllers, a distributed event-triggered mechanism is introduced for the DT optimal controller. The event-triggered condition is detected periodically and therefore naturally avoids the Zeno phenomenon. The closedloop system stability is proved by the Lyapunov synthesis for switched systems. The generation cost minimization and average bus voltage regulation are obtained at the equilibrium point.Finally, switch-level microgrid simulations validate the performance of the proposed optimal controller.

I. INTRODUCTION

WITH the increasing penetration of distributed generators(DGs) and the development of power electronics technology, DC microgrids have gained more and more popularity in recent years [1]–[3]. Freeing of issues such as frequency synchronization and reactive power flow, DC microgrids serve as a superior alternative to their AC counterparts [4]. Additionally, considering the DC nature of many DGs and the proliferation of DC loads, DC microgrids allow the system to have fewer conversion stages and higher energy efficiency [5].

To fully exploit the potential of the DC microgrids, DGs need to be well coordinated. The decision-making objectives in DC microgrids operation are to achieve stability and optimality. The former achieves load sharing and voltage regulation to ensure that the currents and voltages in microgrids are dynamically stable, and the latter minimizes the costs or losses [6], [7]. Over the past decade, centralized[8] or distributed [9] hierarchical controls are widely adopted in DC microgrids to achieve these objectives. However, they are realized at different control levels with different timescales, resulting in increased response time and degraded optimization performance [10].

To solve this problem, control schemes [11]–[15] that can simultaneously realize stability and optimality are proposed for DC microgrids. The key is to achieve optimal load sharing that directly minimizes the cost or losses instead of simple proportional load sharing. In [11] and [12], distributed controllers are proposed to achieve optimal load sharing and average bus voltage regulation in DC microgrids, the optimal objectives are to realize unconstrained transmission loss and operating cost minimization, respectively. However, the lack of generation constraints [11], [12] can lead to overloads and hardware damages. To ensure the satisfaction of generation constraints, a distributed unified controller is presented in[13], which achieves cost minimization and average bus voltage regulation by using the equal incremental cost criterion.To further improve the voltage regulation performance,distributed optimization algorithms are presented in [14], [15]to solve the optimal power flow (OPF) problem for DC microgrids. However, all these control strategies [11]–[15]require high-bandwidth communication links, leading to increased costs and communication congestion [16].

To lower the communication requirement, event-triggered or self-triggered mechanisms are suggested [17], in which communications occur passively or actively only when it is necessary. Applications of these mechanisms for DC microgrid control have been reported in [18]–[20], where proportional load current sharing and average bus voltage regulation are achieved. However, [18]–[20] are designed in the continuous-time (CT) domain, which requires CT event monitoring and may be susceptible to the Zeno phenomenon,i.e., infinite events occur over a finite time interval. To resolve this issue, DT control schemes with trigger mechanisms[21]–[23] are suggested. Due to the DT event monitoring, they are inherently immune to the Zeno phenomenon. In [21], a periodic event-triggered (PET) control scheme is proposed to achieve proportional load sharing and average bus voltage regulation. Further, a distributed DT self-triggered control scheme is proposed in [22] to deal with the data dropouts and communication delays. In [23], the objectives of proportional load sharing and average bus voltage regulation are formulated as an optimal control problem and solved by a distributed consensus-based event-triggered control scheme.Nevertheless, the aforementioned studies [18]–[23] cannot achieve the optimal load sharing with minimized cost or losses.

In summary, control strategies with reduced communication requirement that can simultaneously realize stability and optimality in DC microgrids are still lacking. The main difficulty lies in developing an effective method that not only ensures the satisfaction of generation constraints but also is simple enough for trigger mechanism designs. In present control designs [13]–[15], project operators are usually utilized to ensure the satisfaction of generation constraints.But their nonlinearity and non-smoothness make these control designs difficult to incorporate with distributed trigger mechanisms. Consequently, a simple yet effective control method is needed to take into account generation constraints before trigger mechanisms can be introduced to reduce the communication requirement.

To this end, this study presents a distributed PET optimal control scheme based on a virtual incremental cost. The objectives are to simultaneously achieve generation cost minimization with generation constraints and average bus voltage regulation in DC microgrids. First, the mathematical model of a multiple-bus DC microgrid is established and the optimal control objectives are formulated. Thereafter, a virtual incremental cost with constraint consideration is designed,based on which an optimality condition is derived. With the help of the optimality condition, a distributed DT optimal control scheme is then proposed to achieve the control objectives. Thanks to the simple structure of the optimality condition, a distributed PET optimal control strategy is developed based on the DT scheme to reduce the communication requirement. Finally, the closed-loop system stability is ensured through the Lyapunov synthesis. The performance of the developed controller is validated through simulations.

The main contributions are listed as follows:

1) A virtual incremental cost is designed to accommodate the generation constraints of the DGs, based on which an optimality condition is derived to facilitate the control design.

2) A distributed DT optimal control scheme is proposed to simultaneously achieve the generation cost minimization and average bus voltage regulation. The DT design is inherently suitable for digital controllers and communication systems.

3) A distributed PET mechanism is developed for the DT optimal control scheme. The communication requirement is significantly reduced, and the Zeno phenomenon is avoided.

4) The closed-loop system is formulated as a switched system and proved to be asymptotically stable. The generation cost minimization and average bus voltage regulation are ensured at the equilibrium point.

The remainder of this article is organized as follows:Section II presents the considered DC microgrid model and the problem formulation. The virtual incremental cost and the optimality condition are developed in Section III. The DT and PET optimal controllers are designed in Sections IV and V,respectively, along with the stability analyses. In Section VI,simulation case studies are performed. Finally, concluding remarks are given in Section VII.

II. PROBLEM FORMULATION

A. Electrical Network Model

An example of the considered multiple-bus DC microgrids is illustrated in Fig. 1. Each DC bus is supported by a converter-interfaced DG whose output voltage can be regulated. To realize distributed control, local DGs are coordinated by local controllers that only exchange information with their immediate neighbors through a sparse communication network. Since the DC distribution lines are predominantly resistive, the dynamic effects of line capacitors and inductors are neglected [21], [22] to simplify the control design.

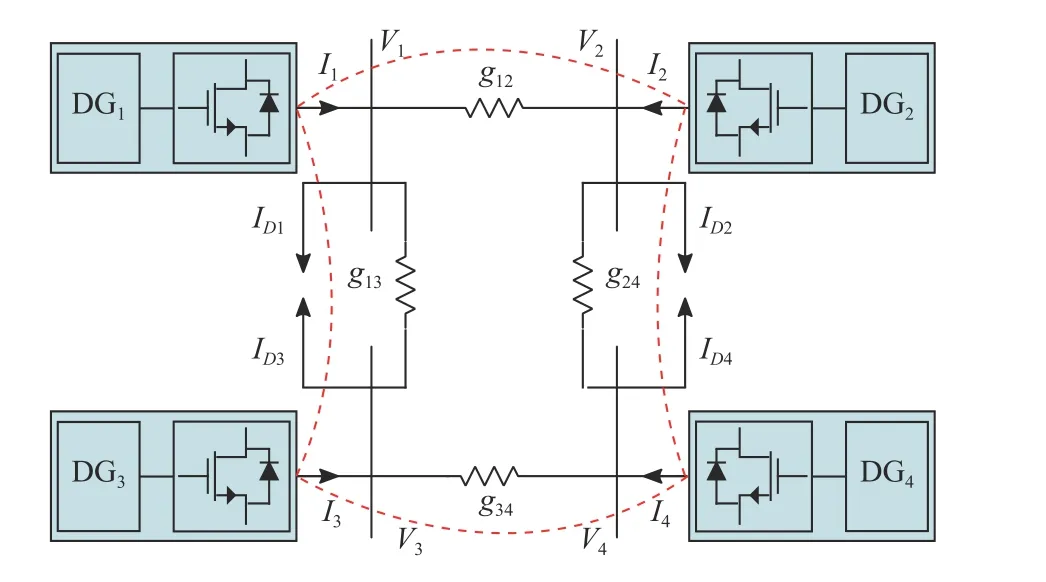
Fig. 1. Multiple-bus DC microgrids. Dash lines: communication network.

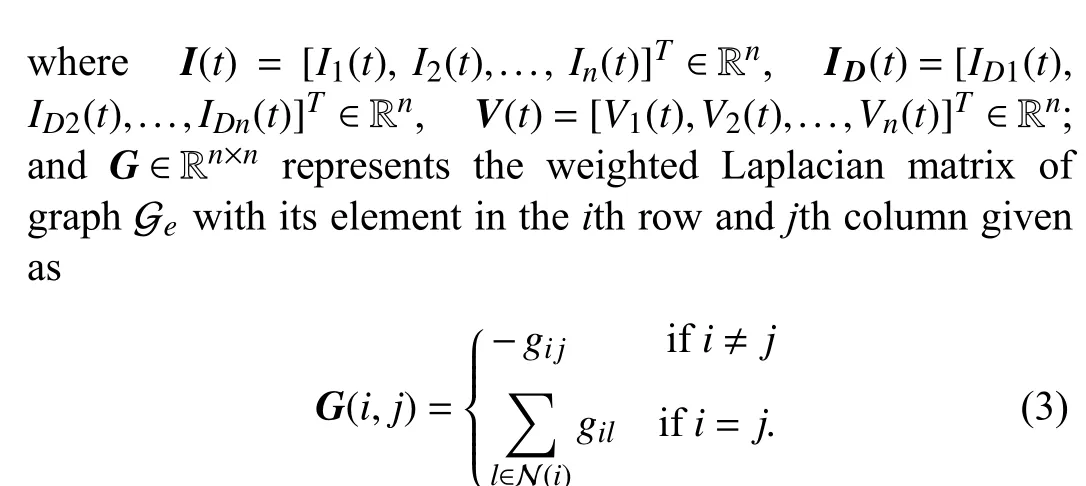
Note thatGis generally referred to as the nodal admittance matrix in power engineering.

B. Generation Cost and Constraints

,

C. Optimal Control Objectives

To improve the energy efficiency and ensure the safe operation of the DC microgrid, two control objectives are considered in this study, i.e., generation cost minimization and average bus voltage regulation.

III. OPTIMALITY CONDITION BASED ON VIRTUAL INCREMENTAL COST

To achieve the control objectives through distributed control algorithms, the optimization problem is first analyzed in this section. A virtual incremental cost is designed to accommodate the generation constraints of the DGs, based on which an optimality condition is derived to facilitate the control design.

A. Equal Incremental Cost Condition

For a multiple-bus DC microgrid, only DG output voltages are generally independently controlled via converters, the output currents are indirectly controlled via voltages. Since the control objectives of generation cost minimization and average bus voltage regulation involve both currents and voltages, the goal of this study is to develop voltage control designs that can simultaneously achieve these objectives.

If all DGs operate within the output current limits, the simple optimality condition (9) allows for voltage control designs that can achieve not only generation cost minimization but also average bus voltage regulation.However, when some DGs are required to generate output currents exceeding their limits based on (9), these DGs will switch to current control mode and keep their output currents at their limits, while the remaining DGs operate at the equal incremental cost for generation cost minimization [10], [13].Under such a condition, the bus voltage regulation performance will be jeopardized.

B. Virtual Incremental Cost with Constraints Consideration

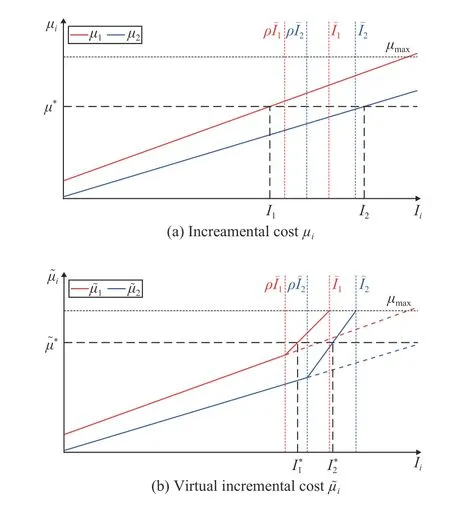
Fig. 2. Illustrations of µi and ～µi.

IV. DISTRIBUTED DT OPTIMAL CONTROL DESIGN

To achieve the control objectives, a distributed DT optimal controller is proposed in this section before introducing the event-triggered mechanism.

A. DT Sampling

Considering that digital controllers and digital communication systems are the foundation of modern control systems, it is preferable to directly design DT controllers based on DT sampled signals of the system.

B. Distributed DT Optimal Control Design

C. Equilibrium Point and Stability Analysis

Since the bus voltageVican track its referenceVref(i)quickly and accurately with the help of converter inner control loops, the dynamics of DGs is hence neglected to simplify the analysis. As a result, it is assumed thatVi=Vref(i)in the following analyses [19].

Rewriting (15) in a compact form yields the voltage dynamics of the DC microgrid with the proposed DT optimal controller

Proof:Please see Appendix A.

From Lemma 1, one can notice that the control objectives can be achieved if the microgrid converges to the equilibrium points. The convergence analysis of the proposed DT optimal controller is presented in the following theorem.

Theorem 1:Consider a DC microgrid modeled as (2) and controlled by the distributed DT optimal controller (15). Then the DG output currents and bus voltages converge to their equilibrium points characterized by (19), (20) asymptotically.The control objectives of generation cost minimization and average bus voltage regulation are achieved.

Proof:Please see Appendix B.

V. DISTRIBUTED PET OPTIMAL CONTROL DESIGN

For the distributed DT optimal controller (17), each local controller needs to periodically update its control signal and communicates its local information ～µito its neighbor(s). In practice, it is preferable for local controllers to send information to their neighbors only when it is required.Therefore, a distributed PET mechanism is developed for (17)in this section to reduce the communication traffic.

A. Periodic Event-Triggered Mechanism

B. Distributed PET Optimal Controller Design

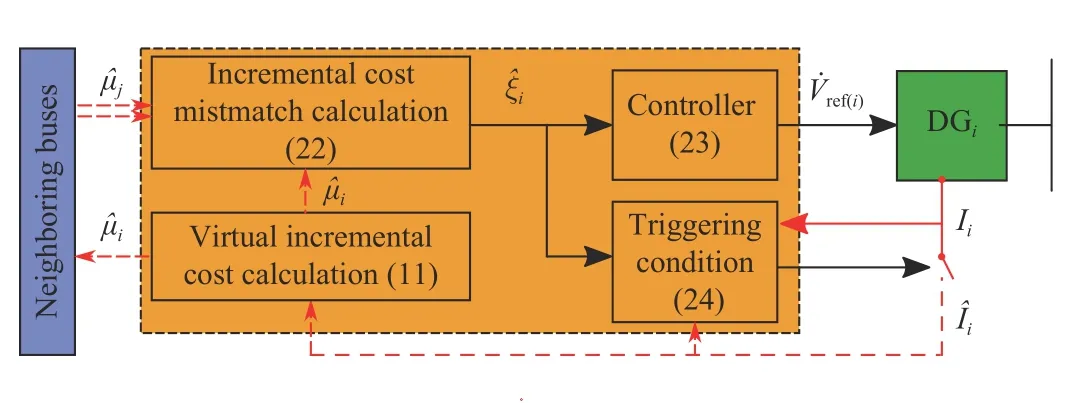
Fig. 3. Structure of the distributed PET optimal controller.

C. Equilibrium Point and Stability Analysis

Rewriting (23) in a compact form yields the voltage dynamics of the DC microgrid with the proposed PET optimal controller

Similarly, the convergence analysis of the proposed PET optimal controller is presented in the following theorem.

Theorem 2:Consider a DC microgrid modeled as (2) and controlled by the distributed PET optimal controller (23)along with the triggering condition in (24). Then the DG output currents and bus voltages converge to their equilibrium points characterized by (19), (20) asymptotically. The control objectives of generation cost minimization and average bus voltage regulation are achieved.

Proof:Please see Appendix D.

VI. CASE STUDIES

To verify the effectiveness of the proposed distributed PET optimal controller, a switched-level DC microgrid illustrated in Fig. 1 is simulated. The model is developed using the Simscape Electrical toolbox of MATLAB/Simulink.

A. System Definition

For the simulated DC microgrid, the DGs are modeled as voltage source converters. Parameters of the simulated system are summarized in Table I. Based on these parameters, the upper bounds of the control gainscmaxand εmaxare calculated according to (16), (24), which are 0.0057 and 0.05,respectively. To maintain a certain safety margin for uncertainties, values of controller parameters are chosen as in Table II. To realize the bus voltage referenceVref(i), cascaded proportional-integral (PI) control loops are utilized. The PI gains are carefully selected to ensure that the voltage references can be quickly and accurately realized by the inner control loops.

TABLE I SYSTEM PARAMETERS

B. Case I: Performance Comparison

In this case, the performances of the proposed PET and DT optimal controllers are compared. The DC microgrid is subjected to various loading conditions as summarized in Table III. Initially, local loads are powered by local DGs and the bus voltages are all set to 1 p.u. The proposed controllers are deployed at 1 s. Afterward, additional load changes are introduced at 3 s and 5 s, respectively. The comparison results are shown in Figs. 4 and 5.

The performance of the proposed distributed PET optimal controller is shown in Fig. 4. As demonstrated in Figs. 4(a) and4(b), converter output voltages and currents converge to the steady-state value within 0.5 s when the controller is deployed at 1 s. At 3 s, loads at all buses are increased, andload1becomes larger than the 1 p.u.. Even though the converter output currentI1initially exceeds the converter limits due to the load change, the proposed PET optimal controller quickly regulates it to the converter limits within 0.5 s. It demonstrates the output current regulation capability of the proposed controller. Finally, similar performance can be observed when additional load changes are introduced at 5 s.

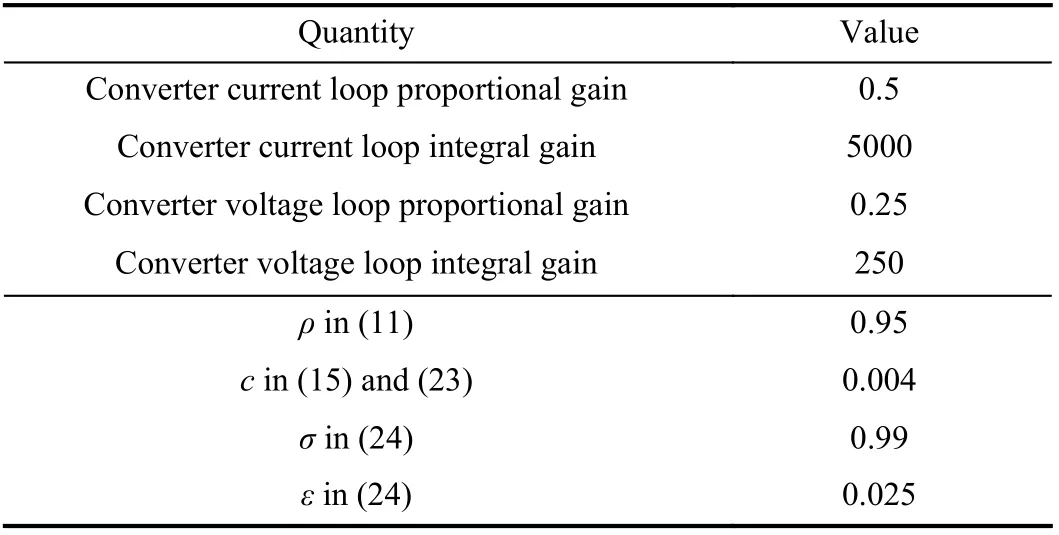
TABLE II CONTROL PARAMETERS

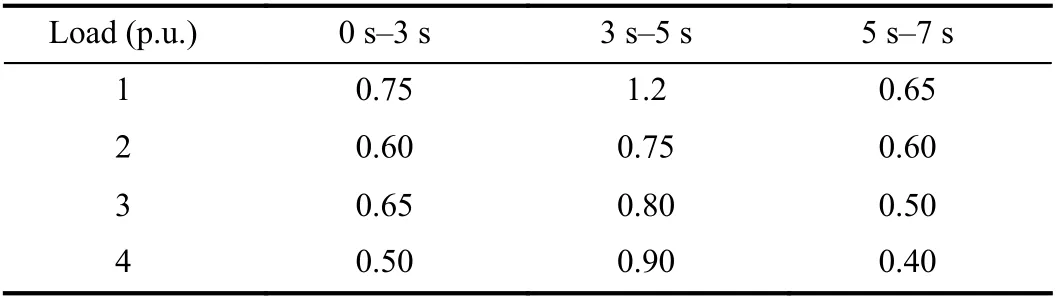
TABLE III LOAD SETTINGS

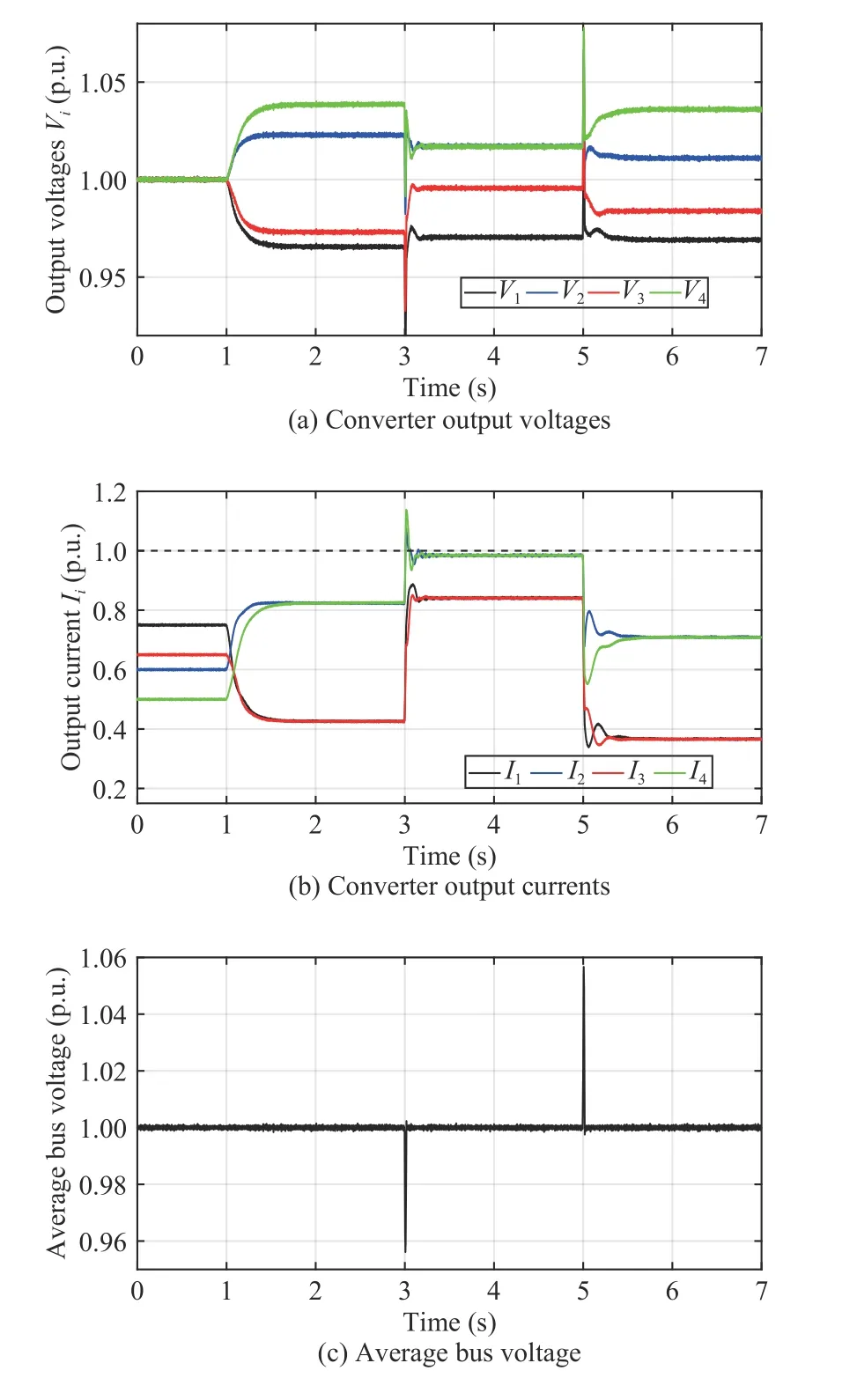
Fig. 4. Control performance of the distributed PET optimal controller.

Fig. 5. Control performance of the distributed DT optimal controller.

To validate the optimality of the proposed distributed PET optimal controller, the ground truth of the optimization problem P1 is solved by the convex optimization algorithm in MATLAB, and the two results are compared in Table IV. One can notice that when the stead-state currents are smaller than their limits, the errors between the generation cost of the proposed method and that of the ground truth are close to zero. When some steady-state currents are kept at the current limits (from 3 s to 5 s), the error becomes larger since only near-optimal solution is obtained by the proposed method,which is smaller than 0.6%. Hence, the proposed method can achieve generation cost minimization.

Furthermore, Fig. 4(c) demonstrates the average bus voltage performance of the proposed PET optimal controller. Notice that average bus voltage is maintained at the nominal value of 1 p.u. in the steady-state as designed. Hence, the proposedmethod can also achieve average bus voltage regulation.

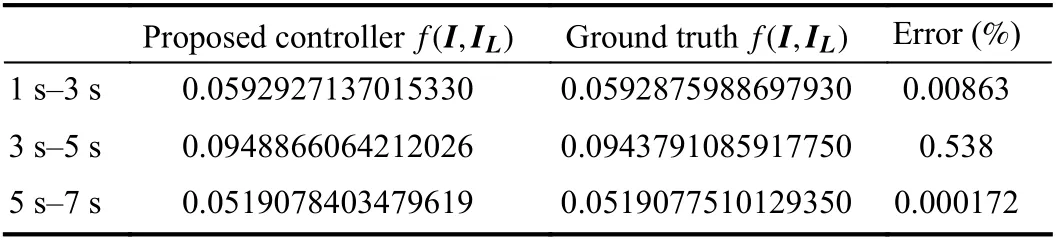
TABLE IV OPTIMALITY VALIDATION

Fig. 6(a) shows the triggering instants of the proposed PET optimal controller. It is evident that more frequent communications are triggered when control deviations are large, i.e.,immediately after the load changes at 1 s, 3 s, 5 s, whereas the communications among controllers decrease when the system approaches the steady-state. This means that the algorithm can dynamically adjust communication demands based on operating conditions, which significantly reduces overall communication traffic. As demonstrated in Fig. 6(b), the DT optimal controller needs to communicate 12 000 (4 × 3000) times,while the PET one only requires about 664 times in total.

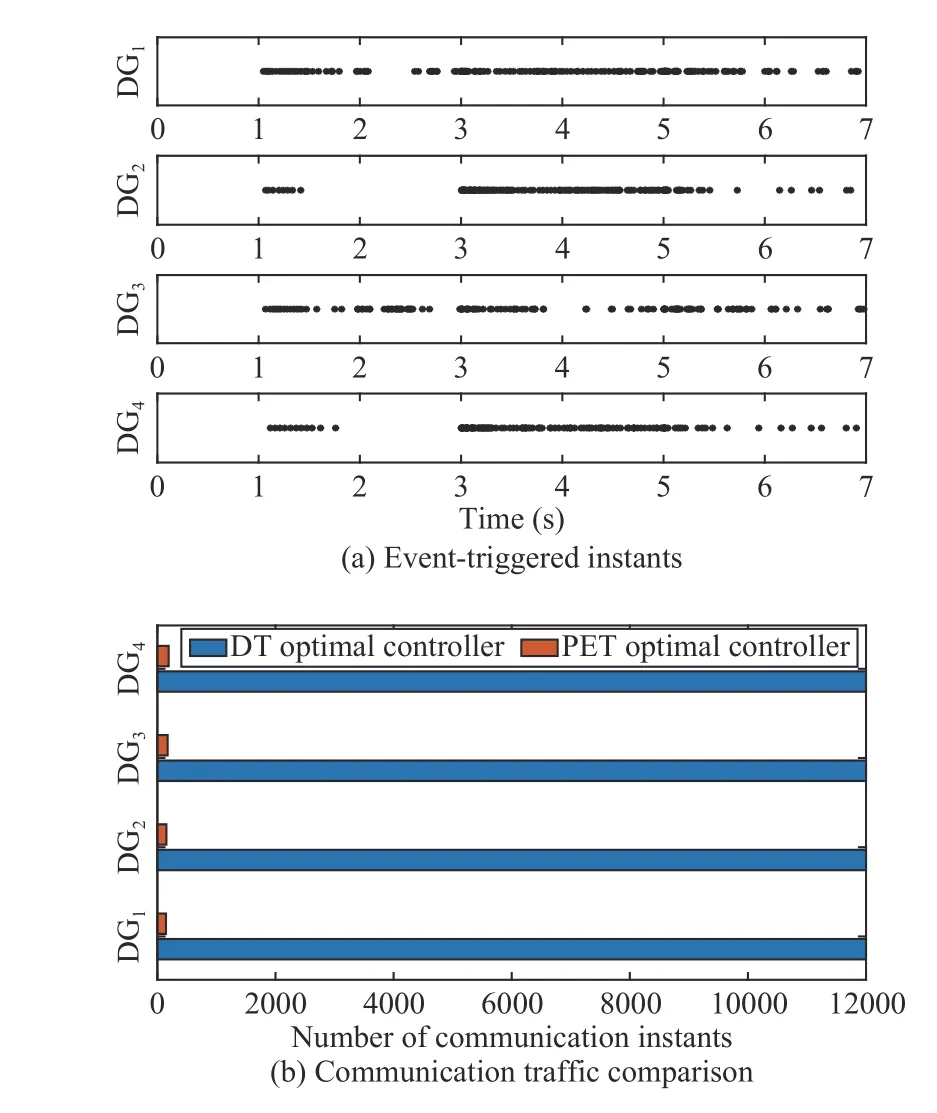
Fig. 6. Event-triggered instants and communication traffic comparison.

The performance of the proposed distributed DT optimal controller is shown in Fig. 5. It can be observed that the DT optimal controller has a similar performance as the PET optimal controller. However, the communication traffic of the PET optimal controller is significantly lower than the DT optimal controller, which is illustrated in Fig. 6.

C. Case II: Communication Delay Studies

In this case, the proposed PET optimal control is tested with constant communication delays. The DC microgrid is subjected to the same load changes in Case I.

Fig. 7. Control performance of the distributed PET optimal controller with a 2-ms communication delay.

Fig. 7 illustrates the performance of the PET optimal controller with a 2-ms communication delay. It can be observed that the control performance is similar to the one in Fig. 4. This is attributed to the fact that the proposed controller is implemented with a sampling period ofT=2 ms.Since the local information is only required to be communicated to its neighbors within 2 ms, the effects of the 2-ms communication delay can thus be reduced.

The performance of the PET optimal controller with a 6-ms communication delay is shown in Fig. 8. It can be observed that even though the system is stable, there are significant voltage and current oscillations. A further increase in the communication delay may destabilize the system.

In conclusion, the proposed PET optimal controller can withstand a 6-ms communication delay or less. A smaller control gaincand a longer sampling periodTcan be selected to alleviate the effects of communication delays.

VII. CONCLUSION

In this article, a distributed PET optimal control scheme is proposed to achieve the generation cost minimization and average bus voltage regulation in DC microgrids. The designed virtual incremental cost helps to accommodate the generation constraints of DGs. The DT control design is inherently suitable for digital control and communication systems. The PET mechanism not only reduces the communication requirement but also avoids the Zeno phenomenon. The closed-loop system stability and convergence of the proposed control strategy are proved by the Lyapunov synthesis for switched systems. Simulation studies validate the control performance.

Fig. 8. Control performance of the distributed DT optimal controller with a 6-ms communication delay.

APPENDIX A PROOF OF LEMMA 1

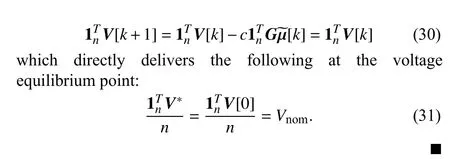
APPENDIX B PROOF OF THEOREM 1

APPENDIX C PROOF OF LEMMA 2

I[k+1]=I[k]ˆξ∗=0

Setting in (26) yields that at the current equilibrium point. Additionally, according to the triggering condition (24) we have

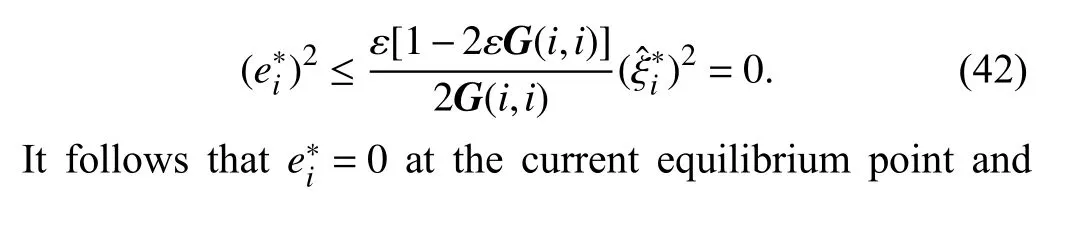
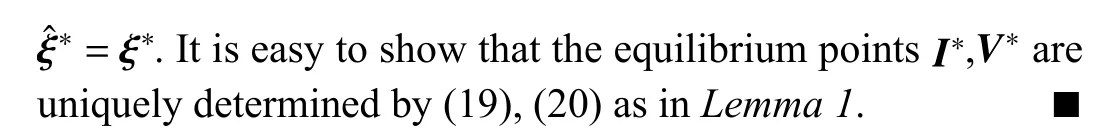
APPENDIX D PROOF OF THEOREM 2