Coordination of Networked Nonlinear Multi-Agents Using a High-Order Fully Actuated Predictive Control Strategy
2022-04-15GuoPingLiu
Guo-Ping Liu,
Abstract—This paper is concerned with the coordinative control problem of networked nonlinear multi-agents (NNM)with communication delays. A high-order fully actuated (HOFA)model is introduced to describe the nonlinear multi-agents. Based on this model, a HOFA predictive coordination method is proposed to compensate for the communication delays actively and achieve simultaneous stability and consensus. This method largely simplifies the design of networked nonlinear multi-agents and makes the control performance be same for networked nonlinear multi-agents with and without communication delays.The analysis on the closed-loop systems derives the simultaneous stability and consensus criteria of networked nonlinear multiagents using the HOFA predictive coordination method. With the presented way of designing HOFA predictive coordination controllers, a simulated example demonstrates the advantages of the proposed method.
I. INTRODUCTION
THE rapid development of network technology accelerates the development of networked multi-agent systems, such as the Internet of things and industrial Internet systems. A networked multi-agent system is a multi-dimensional complex system integrating communication networks and physical environments. Through the integration of computing,communication and control technologies, it can realize the real-time perception, dynamic control and information service of large-scale engineering systems, make the systems more efficient and coordinative, and have important and wide application prospects [1]–[3]. Networked multi-agent systems have widely been used in the fields of energy, manufacturing,aerospace, telemedicine, etc. Due to the introduction of networks, there are inevitably communication constraints,such as delays, loss, disorder and attacks on data, which bring great challenges to the design and analysis of networked multi-agent control systems [1].
Much research work has been carried out on the influence of communication constraints (particularly, network delays)on the control performance (e.g., consensus) of networked multi-agent systems [4], [5]. The main methods of dealing with the consensus problem of networked multi-agent systems are the time-delay system method, switching system method,Markov jump system method, stochastic system method,event-triggered control method, etc. The time-delay system method transforms the networked multi-agent control system into a system with variable time-delays so that the system can tolerate a maximum time-delay upper bound and maintain a certain expected system performance [6]. The switching system method describes the networked multi-agent system under bounded uncertain data delay and packet loss effects as a discrete-time system with arbitrary switching so that the existing switching control system theory can be applied directly [7]. The Markov jump system method focuses on the Markov chain characteristics of network delays, and constructs the networked multi-agent system as a Markov jump system for consensus analysis [8]. The stochastic system method provides a powerful tool for analysing the system consensus of networked multi-agent systems with random communication constraints [9]. The event-triggered control method can greatly improve the resource utilization of the networked multi-agent system, but the control performance changes little [10]–[12]. Generally speaking, most control methods of networked multi-agent systems use a passive way to suppress communication constraints, which makes the consensus conditions of the system relatively conservative.
For the communication constraints in networked multi-agent systems, the predictive control strategy has incomparable advantages over other control methods. Considering how to compensate for communication constraints actively and taking advantage of the characteristics that a network can transmit data in packets, the networked predictive control method has been proposed [13]. This method breaks through the traditional control mode of point-to-point single data transmission, and adopts the idea of predictive control to compensate actively for the communication constraints in a networked multi-agent system so that its control performance is almost the same as that of the system without networks.Following the networked predictive control strategy, a networked multi-agent predictive control method has been proposed to compensate for network delays of multi-agents with a directed topology and non-uniform agents via a distributed dynamic output feedback protocol [14]. To solve the simultaneous stability and consensus problem of networked multi-agent systems with communication delays and data loss, further design and analysis of the networked multi-agent predictive control systems has provided the necessary and sufficient conditions of achieving both output consensus and input–output stability [15]. Then, a cloud predictive control scheme for networked multi-agent systems has been presented to reduce the expenses for establishment,operation, and maintenance of the systems tremendously based on its computational efficiency and speed via cloud computing [16]. Although a great number of research achievements have been made in networked multi-agent predictive control [17], [18], most of them focus on linear multi-agents. How to deal with nonlinearities of multi-agents needs further research.
Nowadays, most of nonlinear control systems are generally described in the form of a first-order state space model. Based on this model, several nonlinear control methods have been applied to networked nonlinear multi-agent systems, such as the feedback linearization method [19], the back-stepping method [20], the sliding mode method [21], [22], the Lyapunov method [23]. But, there are still various restrictions on those methods. For example, the feedback linearization method needs strong Lie differentiable conditions, the backstepping method is employed only for a special class of systems with a triangular model form, and the Lyapunov method needs to find appropriate Lyapunov functions which are not unique. Generally, it is hardly to realize the global stabilisation and consensus of networked nonlinear multiagent control systems even in the case of no communication constraint.
According to the high-order fully actuated (HOFA) system approach [24], most of physical nonlinear systems can be expressed as a HOFA model, which is another system description form and has more universality, simplicity and flexibility for nonlinear system design and analysis. Based on the HOFA model, this paper studies the coordinative control problem of networked nonlinear multi-agents. Two cases are studied: One is the multi-agents without communication delays and the other is the multi-agents with communication delays. For the first case, a HOFA coordination scheme is presented. For the second case, a HOFA predictive coordination method is proposed to compensate for communication delays actively. Both the HOFA coordination scheme and HOFA predictive coordination method achieve simultaneous stability and consensus of networked nonlinear multi-agents.
II. COORDINATED CONTROL OF MULTI-AGENTS WITHOUT COMMUNICATION CONSTRAINTS
There are various mathematical models to describe physical control systems, such as the first order state space model and the transfer function model. Following the HOFA system approach [24], then-th order fully actuated discrete-time model is utilised to represent nonlinear multi-agents as follows:

Actually, the combination of (9) and (10) forms the closedloop networked nonlinear multi-agent system without communication constraints using the HOFA coordination scheme.
III. COORDINATED CONTROL OF MULTI-AGENTS WITH COMMUNICATION DELAYS
In networked multi-agents, there usually exist various communication constraints, for example, delays, data loss,attacks, quantisation, synchronisation, etc. For the sake of simplicity, only the communication delays are considered here. Let the communication delay from thej-th agent to thei-th agent be fixed and denoted bysij, and
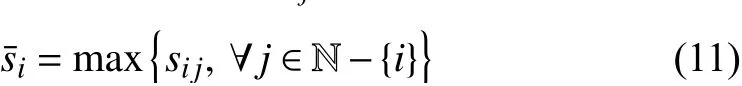
be the largest communication delay from all other agents to thei-th agent.
To simplify the presentation, it is also assumed that all the agents of networked nonlinear multi-agents are fully connected via communication networks. This will also make the calculations of the output predictions of all the agents much easier. The most effective way of compensating for the communication delays is the predictive control strategy. In the case of the communication delays, following scheme (6), a HOFA predictive coordination scheme of the agents is proposed as follows:


which is needed in (13). The stability and consensus of the closed-loop networked nonlinear multi-agent system using the HOFA predictive coordination method proposed in this section will be analysed in the next section.
and
IV. SIMULTANEOUS STABILITY AND CONSENSUS ANALYSIS OF CLOSED-LOOP MULTI-AGENT CONTROL SYSTEMS
A networked multi-agent control system can achieve consensus, but it does not imply that the stability of the system is guaranteed, which is usually ignored by most researchers.For practical applications, both the consensus and stability of a networked multi-agent control system should simultaneously be analysed. Following Definition 1 in [15], a definition is introduced below.
Definition 1:Networked multi-agent control system (1) with controller (12) achieves input-output stability and output consensus simultaneously if

which are induced from (9) and (10), respectively. Similarly,the following results for (20) and (21) can recursively be derived:

which is the same as (10) of the networked nonlinear multiagents without communication delays. So, the closed-loop systems for the two cases (one is with communication delays and the other is without communication delays) are exactly the same when the HOFA coordination scheme or HOFA predictive coordination method is employed.
Equation (38) can compactly be expressed as


Clearly, all the networked nonlinear agents achieve consensus. According to Definition 1, it can be concluded that the networked nonlinear multi-agents are of simultaneous stability and consensus using the HOFA predictive coordination method. Therefore, summarising the above gives the following theorem.
Theorem 1:Networked nonlinear multi-agent (1) with the HOFA coordination controller (6)–(8) or HOFA predictive coordination controller (12)–(14) achieves simultaneous stability and consensus if and only if matrixHin (43) is Schur stable.
Remark 1:The key advantage of the HOFA system approach is to remove the nonlinearities of a nonlinear system and transform it to a desired linear system through the controller design. When this approach is applied to design the controller of a networked nonlinear multi-agent system,Theorem 1 shows that the stability and consensus conditions of the closed-loop system are related only to both its transformed linear system and the linear part parameters of the controller.
V. DESIGN OF THE AGENT CONTROLLER PARAMETERS
There are many ways to design the parameters of the HOFA predictive coordination controllers of networked nonlinear multi-agents. This section presents two steps to determine those parameters.

Clearly, the first step guarantees that the individual agents are stable and have the desired control performance when there is no coordination between the agents. The second step ensures that all the networked multi-agents coordinate with simultaneous stability and consensus.
VI. AN EXAMPLE
To illustrate the performance of the HOFA predictive coordination method for networked nonlinear multi-agents with communication delays proposed in this paper, an example is provided in this section. Three different order fullyactuated discrete nonlinear agents are considered as follows:l

The communication graph of the networked three-agent system is assumed to be fully connected, as shown in Fig.1.
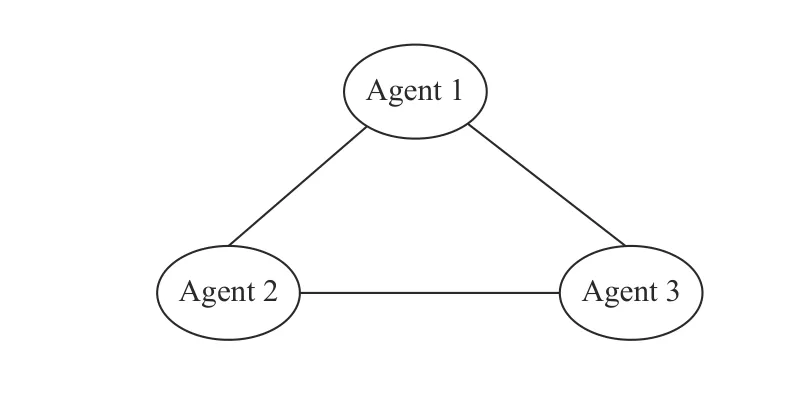
Fig. 1. The communication graph.
Following the two steps of designing the PI and coordinative parameters introduced in Section V, firstly, let the coordinative parameters be zeros and chooseq1=q2=q3=0in (8) to make the characteristic equation (49) of the individual agents become
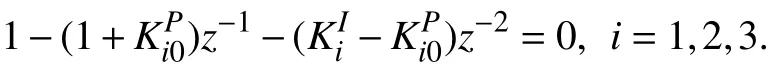
To assign the closed-loop poles of the three agents at 0.91±0.21j(Agent 1), 0.92±0.22j(Agent 2) and 0.93±0.23j(Agent 3), which provide good transient dynamical performance, using the pole assignment method leads to the following PI parameters:

which are within the unit circle. So, according to Theorem 1,the closed-loop networked three-agent system is stable and all the three agents also achieve the output consensus.
Let the reference inputr(t) be a given square wave with the period of 300 steps and amplitude between 1 and –1. Four cases are illustrated here to compare the performance of the different control strategies: no coordination, coordination without communication delays, coordination without compensating for communication delays, and coordination with compensating for communication delays.

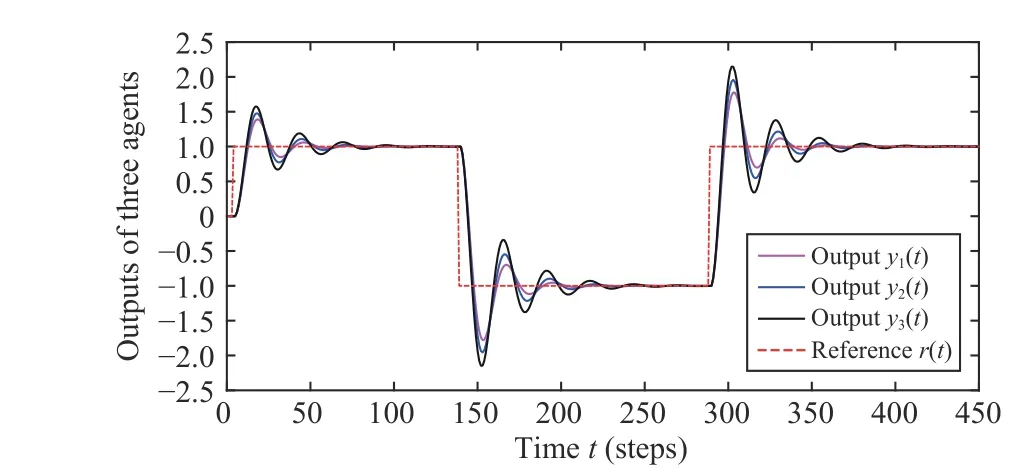
Fig. 2. The output responses of the three agents (Case 1).
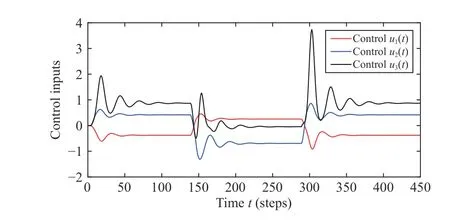
Fig. 3. The control inputs of the three agents (Case 1).
Case 1:No coordination fori= 1, 2, 3. The output responses of the three agents shown in Fig. 4 illustrate that there exists not only the large steadystate error between the reference and the output of each agent but also the significant difference between three agent outputs.
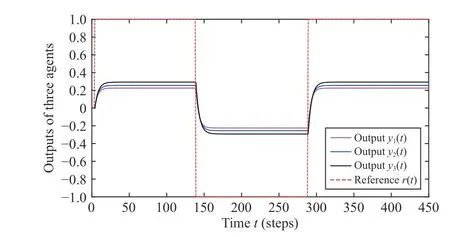
Fig. 4. The output responses of the three agents without the integrator(Case 1).
Case 2:Coordination without delays
This case assumes that there is no communication delay between networked three agents, i.e., the communication delayssij= 0, fori,j= 1, 2, 3,i≠j. Then, from (12) and (13),the controllers of the three agents are
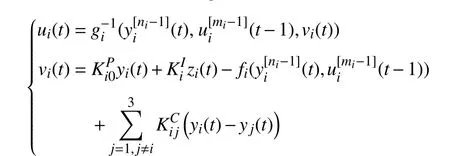
fori= 1, 2, 3. Using those controllers, the output responses and control inputs of the three agents are shown in Figs. 5 and 6. The simulation results demonstrate that all the outputs of the three agents are almost the same. So, the coordination of the three agents is achieved.
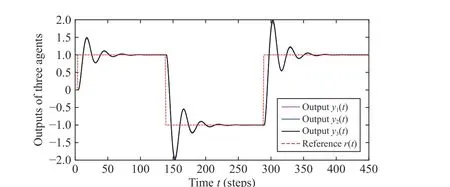
Fig. 5. The output responses of the three agents (Case 2).
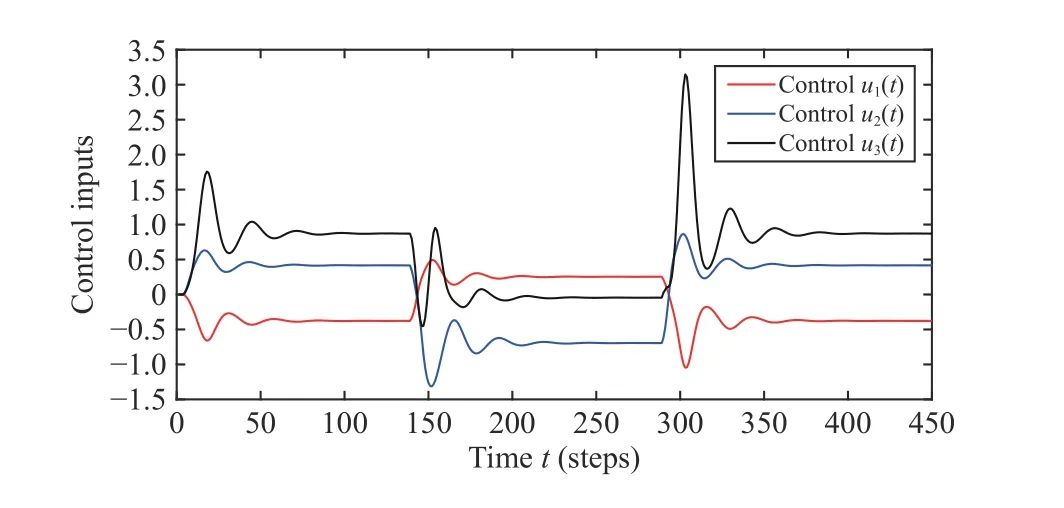
Fig. 6. The control inputs of the three agents (Case 2).
Case 3:Coordination without compensating for delays
There usually exist communication delays between networked multi-agents. Here, it is assumed that the communication delays between the three agents are below:

fori= 1, 2, 3. For this case, the output responses and control inputs of the networked three agents are shown in Figs. 7 and 8. The results indicate that all the three agents without compensating for the communication delays between the agents are unstable.
Case 4:Coordination with compensating for delays

Fig. 7. The output responses of the three agents (Case 3).
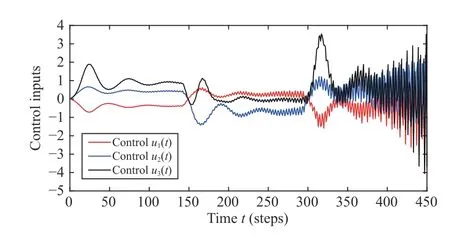
Fig. 8. The control inputs of the three agents (Case 3).
The active compensation strategy for delays is applied when there exist communication delays between networked three agents. The proposed HOFA predictive coordination controllers (12) and (13) of the agents for this case are fori= 1, 2, 3. Employing the above controllers, the output responses and control inputs of the three agents with communication delays given in Case 3 are shown in Figs. 9 and 10. The simulation results demonstrate that all the three agents achieve simultaneous stability and consensus, and the control performance is exactly the same as the one of Case 2.It also shows that the communication delays between the three agents are completely compensated by the HOFA predictive coordination method presented in Section III.

Fig. 9. The output responses of the three agents (Case 4).
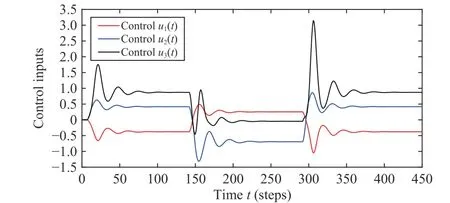
Fig. 10. The control inputs of the three agents (Case 4).
VII. CONCLUSIONS
This paper has addressed the coordinative control problem of a class of networked nonlinear multi-agents. To compensate for communication delays, a HOFA predictive coordination method has been proposed to make the closedloop networked nonlinear multi-agent system achieve simultaneous stability and consensus. Compared with other existing coordination methods of networked nonlinear multiagents, the HOFA predictive coordination method is simple,active and universal. Also, it has two important advantages:firstly, the control performance of the closed-loop networked multi-agents is the same in the two cases: with communication delays and without communication delays; Secondly, the necessary and sufficient conditions derived for the simultaneous stability and consensus of networked nonlinear multi-agents are independent of communication delays. The parameters of the HOFA predictive coordination controller are designed in two steps. The simulation results illustrated in this paper have confirmed the above advantages. In fact, there still exist various challenges on the HOFA predictive coordination of networked nonlinear multi-agents. They include the internal nonlinear uncertainties (such as modelling error), external uncertainties (such as random disturbances), and time-varying communication constraints in most practical multi-agent systems. A possible way to overcome those challenges will be to combine the proposed method in this paper with other existing control methods, for example, robust control methods, adaptive control methods, disturbance rejection methods, networked control methods and so on. The proposed HOFA predictive coordination method still needs further research to deal with those challenging issues.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Energy Theft Detection in Smart Grids: Taxonomy,Comparative Analysis, Challenges, and Future Research Directions
- On the System Performance of Mobile Edge Computing in an Uplink NOMA WSN With a Multiantenna Access Point Over Nakagami-m Fading
- Continuous-Time Prediction of Industrial Paste Thickener System With Differential ODE-Net
- Unmanned Aerial Vehicles: Control Methods and Future Challenges
- A Braille Reading System Based on Electrotactile Display With Flexible Electrode Array
- A Short-Term Precipitation Prediction Model Based on Spatiotemporal Convolution Network and Ensemble Empirical Mode Decomposition
