Distributed Optimization Algorithm for Multi-Robot Formation with Virtual Reference Center

Jingyi Huang, Shuaiyu Zhou, Hua Tu, Yuhong Yao, and Qingshan Liu,

Citation: J. Y. Huang, S. Y. Zhou, H. Tu, Y. H. Yao, and Q. S. Liu,“Distributed optimization algorithm for multi-robot formation with virtual reference center,”IEEE/CAA J. Autom. Sinica, vol. 9, no. 4, pp. 732–734,Apr. 2022.

J. Y. Huang, S. Y. Zhou, H. Tu, and Y. H. Yao are with the School of Mathematics, Southeast University, Nanjing 210096, China (e-mail: jingyi_huang@seu.edu.cn; sy_zhou@seu.edu.cn; tuhua@seu.edu.cn; yhyao@seu.edu.cn).

Q. S. Liu is with the School of Mathematics, Southeast University, and also with the Jiangsu Provincial Key Laboratory of Networked Collective Intelligence, Nanjing 210096, China (e-mail: qsliu@seu.edu.cn).

Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.

Digital Object Identifier 10.1109/JAS.2022.105473

Dear editor,

In this letter, we use a distributed optimization approach to solve a class of multi-robot formation problem with virtual reference center.We investigate the design and analysis of the constrained consensus algorithm to solve the optimization problem with a sum of objective functions with some local constraints. In the multi-robot system with virtual reference center, each robot has messages on its own constraints and objective function, as well as the message about the formation that interacts with the virtual reference center. At the same time, all the robots collaborate to find the minimum value of the function defined by the formation. To find the optimal formation, we propose an algorithm with fixed step size with better performance. In addition, we use a combination of the Hungarian assignment algorithm and the proposed formation algorithm to get the optimal matching formation of the multi-robot system.

Distributed formation control of multi-robot systems has emerged as an active research area over the past decades. This problem finds applications in different fields, such as path planning, goal searching,formation and rendezvous [1], [2]. Generally, the distributed formation optimization is described with a connected network of many robots. In the literature, distributed formation control of multirobot systems has been extensively studied. For the problem of formation forming and changing, [3]–[5] use the coordination errors between robots to propose a distributed formation control strategy without assuming each robot knowing the complete state of the leader. Reference [6] proposes a control framework in a nonlinear multi-agent system to deal with the problem of distributed faulttolerant containment control (FTCC). For the assignment strategy,[1] proposes a method to assign the best goal to each robot and calculate the collision-free path for each robot to its goal destination iteratively. The convex optimization strategy for a large-scale robot team is considered with both algorithm scalability and real-time performance in [7] and [8]. Besides, [9] investigates the dynamic task assignment for multi-robot system and propose two task assignment strategies.

The main contribution of this letter is the proposition of the distributed optimization with gradient projection (GP) algorithm to minimize the formation distance and the Hungarian algorithm to minimize the assignment cost function. The formation is controlled using the relative position between the robots and the virtual reference center. The simulations are presented to verify the effectiveness of the proposed algorithm with good convergence performance for obtaining the global optimal solution, especially for the case of large-scale formations.

Problem description and formation algorithm: The optimization problem for the distributed multi-robot formation withmrobots is described as

Robotigenerates its new estimate at timek+1 according to the following formula:

For solving the problem, we first subtract the minimum element of each row inC, and subtract the minimum element of each column inC. Then, we can find out the independent zero elements in the matrix(that is, only one 0 element in each row and column). If the number of independent zero elements is the same as the order of the matrix,the assignment is completed. Otherwise, the matrix needs to be adjusted and we need to keep calculating until the number of independent zero elements are equal to the order of the matrix.Finally, we transform all zero elements in matrix into one and the other elements into zero to obtain the optimal matrix. The position of the non-zero element represents the assigned result. For example, if χi j=1, it means that theith robot matches thejth target point.

After obtaining the optimal solution, there is only one element in each row and column of the matrix with the value of 1 and the rest is 0. The position of the non-zero element represents the assigned result. For example, if χi j=1, it means that theith robot matches thejth target point. Then we give the Hungarian task assignment algorithm combining with the proposed formation formulas in Algorithm 1.

Algorithm 1 Distributed Formation Algorithm with Virtual Reference Center Initialization:p, q, h, q0 1: Set , (virtual reference center’s position).Δ,L 2: Calculate and α.3: Initialize the task assignment matrix χ.Iterations:4: while The objective function f is not convergent do k=1 5: for : Maximum number of iterations do i=1:m 6: for do 7: the iterations in (7) in distributed manner.8: end for 9: end for 10: Calculate the assignment matrix χ using the Hungarian algorithm.11: Update q and h according to the new assignment matrix χ.12: Calculate the values of the objective function and output.13: end while 14: return q

Simulation results: In this section, we will show the optimal matching between the initial formation and the optimal formation of the multi-robot system by a simulation example. We consider the formation problem on a two-dimensional plane. We set the target formation is composed of three concentric circles, the number of robots is 48, and the virtual reference center is the origin point. We obtain the optimal solution in (4) by the iterations in (6).

The final result is shown in Fig.1, in which the green points represent the initial positions of robots, the red points form the final formation, and the dotted lines represent the relationship and moving tracks between each robot and the target point. Furthermore, the value of the objective functionfin (1) is shown in Fig.2, from which we can see that the objective function decreases as the algorithm iterates.

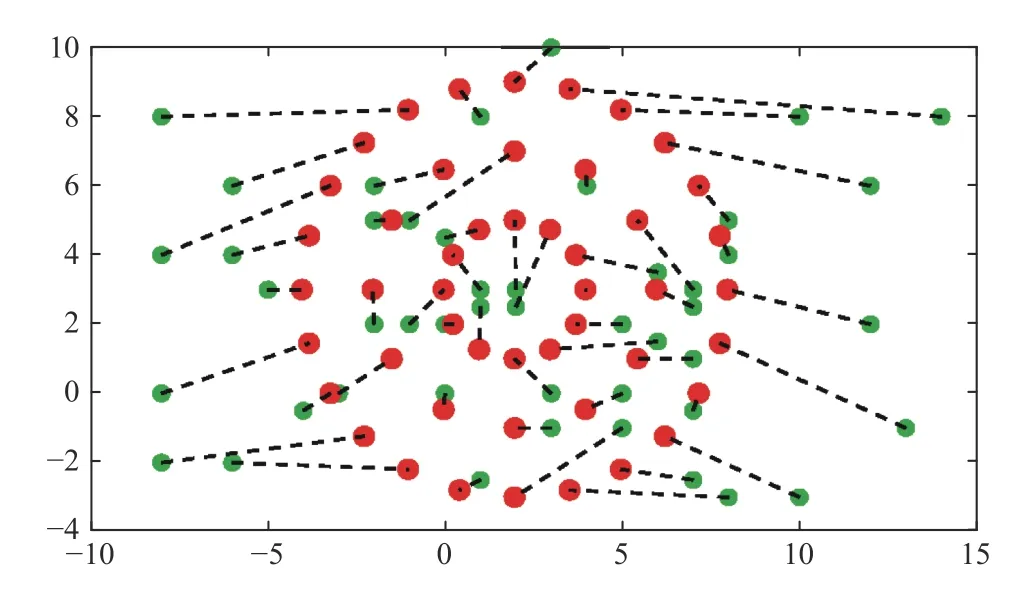
Fig. 1. Optimal formation solved by the proposed algorithm.

Compared with the algorithm in [11] for solving the above formation problem, the proposed algorithm gets the optimal formation after 10 projection iterations and 1 task assignment with 1 outer loop, but the algorithm in [11] needs 20 projection iterations and 1 task assignment with 300 outer loop. Therefore, the proposed algorithm simplifies the iterations with better performance for the scenario of large-scale formation.

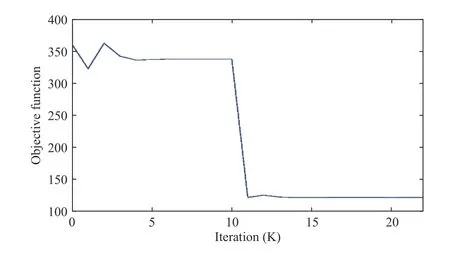
Fig. 2. The evolution of the objective function using the proposed algorithm.

Conclusions: In this letter we propose a fixed step algorithm for multi-robot formation with virtual reference center and analyze its convergence to obtain the global optimal solution. Furthermore, we combine the Hungarian task assignment algorithm with the proposed formation algorithm and apply it to the global formation optimization. The simulation shows the results and some properties of the proposed algorithm. The convergence of the algorithm can be seen to be fast for large-scale formations, which is a potential advantage of the algorithm.

Acknowledgments: This work was supported in part by the National Natural Science Foundation of China (61876036), and the Jiangsu Provincial Key Laboratory of Networked Collective Intelligence (BM2017002).