Searching for Best Network Topologies with Optimal Synchronizability: A Brief Review

Guanrong Chen,

Abstract—The Laplacian eigenvalue spectrum of a complex network contains a great deal of information about the network topology and dynamics, particularly affecting the network synchronization process and performance. This article briefly reviews the recent progress in the studies of network synchronizability, regarding its spectral criteria and topological optimization, and explores the role of higher-order topologies in measuring the optimal synchronizability of large-scale complex networks.

I. INTRODUCTI ON

NETWORK science has grown to be a broad discipline after a continued and persistent research pursuit from various scientific and engineering communities, especially in multi-agent systems, data science, statistical physics, applied mathematics, structural biology and social studies [1]–[3]. In fact, this interdisciplinary field of network science has developed very rapidly in recent years. On the one hand,network science is a self-contained discipline overlapping the classical graph theory developed since the era of Euler in the 18th century [1]–[3], followed by the comprehensive Erdös-Rényi random graph theory [4] and the recent developments of Watts-Strogatz small-world network model [5] and Price-Barabási-Albert scale-free network model [6], [7]. On the other hand, multi-agent systems theory has become indispensable in network science and engineering, offering new approaches to investigating many real-world applications of complex dynamical networks.

Meanwhile, the studies of dynamical synchronization among networked multi-agent systems have developed swiftly with fruitful theoretical results and new findings, particularly from the scientific communities of network science and control systems. Actually, synchronization of coupled systems is one of the oldest scientific research topics, which can be traced back to as early as the Dutch scientist Christian Huygens who in 1665 discovered perfect synchrony of two pendulum clocks fastened to a beam [8]. Since then, the study of synchronization of networks among dynamical systems or oscillators has gone through a long way with many significant results and discoveries, and remains to be a very active research subject in science and engineering today.

The concept of network synchronization may be roughly classified into state synchronization and phase synchronization, but only the former will be addressed by this article. It is well known that in most cases synchronization is a desirable behavior, e.g. coordination of multiple mobile agents, while in other cases it can be undesirable, e.g. data traffic congestions.One typical case in point where synchronization is preferable is its essence for the functioning of biological neuronal systems [9]: “Synchronous behavior of neural assemblies is a central topic in neuroscience. It is known to be correlated with cognitive activities [10] during the normal functioning of the brain, while abnormal synchronization is linked to important brain disorders, such as epilepsy, Parkinson’s disease,Alzheimer’s disease, schizophrenia and autism [11]. Hence the interest is in the topic of neural synchronization, which has been extensively explored theoretically [12].” When synchrony is beneficial, therefore, one would like to maximize it, motivating the current research on optimizing the synchronizability of complex networks. A survey of some earlier research works on various aspects of complex network synchronization is presented in [13].

The currently fast-evolving research direction on network synchronization has created a corpus of exciting opportunities as well as great challenges to both network scientists and system engineers. A complex dynamical network has typically large numbers of nodes and edges, with higher-dimensional dynamical node-systems such as nonlinear oscillators, which are interconnected in some complicated topologies. It took quite a long time for researchers to understand the intrinsic relationship between topology and synchronizability of a general complex network, which turns out to be essential for many real-world applications.

This article briefly reviews the studies of complex network synchronization in relation to the network topologies, focusing on the synchrnizability of general networks with typical topologies such as the aforementioned random-graph networks, small-world networks and scale-free networks, as well as totally homogeneous networks.

Specifically, this article reviews the basic notion and research progress of network synchronization and synchronizability. Section II provides some preliminaries on the general network model and network synchronization formulation. Section III addresses the issue of network synchronizability and presents two criteria. Section IV describes the optimal network synchronizability based on homogeneous topologies. Section V discusses the recent progress in measuring optimal synchronizability using tools from higher-order network topologies. Finally, Section VI concludes the survey with a brief future research outlook.

II. PRELIMINARIES

This section introduces a general network model, which covers the aforementioned random-graph, small-world and scale-free networks, and then describes the general network synchronization problem.

A. Network Model

A diffusively connected, undirected and unweighted continuous-time network ofNidentical node-systems can be described by [14]

B. Network Synchronization Problem

Network (1) is said to achieve (complete state)synchronizationif, and only if,

To derive criteria for achieving synchronization of network(1), spectral analysis based on the network Laplacian eigenvalues (6) is a powerful and effective tool to use, as can be seen above and further discussed below.

In retrospect, the first synchronization criterion for network(1) was established in [16], [17], in terms of the smallest nonzero Laplacian eigenvalue λ2in (6), namely,

III. NETWORK SYNCHRONIZABILITY AND CRITERIA

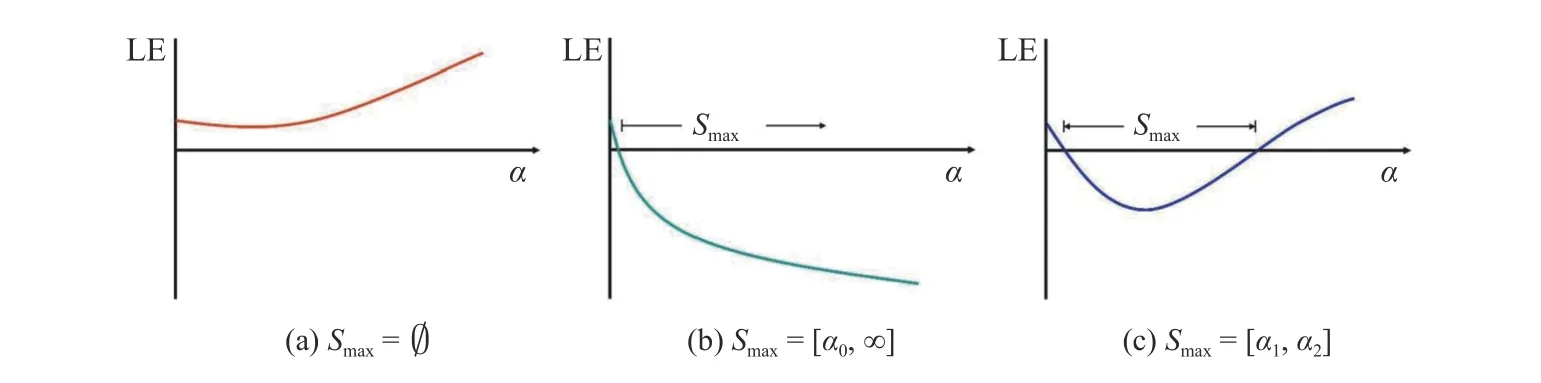
Fig. 1. Network synchronization regions.

These two criteria can be illustrated graphically by Fig. 1,where the curve in each figure is the conditional Lyapunov exponent (LE) of network (1), which can be roughly understood here as the boundary of the Laplacian eigenvalue set [18]. In figure (a), the curve is never negative (i.e., the synchronization region is empty), therefore the network will not be synchronizing. In figure (b), the curve is negative over an unbounded internal [α0,∞) on theα-axis (i.e., the synchronization regionSmaxis unbounded). In figure (c), the curve is negative over a bounded internal [α1,α2] on theαaxis (i.e., the synchronization regionSmaxis bounded).

Later it was found, both numerically [19] and analytically[20], that the network synchronization regionSmaxcan be a union of several intervals, namely the curve in Fig. 1 (c) may bend down and then bend up again alternatively around theαaxis, where the number of bending times depends on the order of the characteristic polynomial of the network Laplacian matrix. In this case, however, it was observed that the eigenratio criterion (9) may not work properly [21] in the case where the synchronization region is a union of several intervals since the ratio might fall into somewhere between two such intervals.

IV. NETWORK TOPOLOGIES WITH BEST SYNCHRONIZABILITY

To compare the synchronization performances of two networks, the concept ofsynchronizabilityis introduced,which refers to the ability of self-synchronizing without external control input or structural perturbations. The interest here is to compare two networks to see which one has a“better” synchronizability in the sense that it is easier or faster synchronizing and/or has stronger robustness in resisting perturbations, so that the eigenvalue λ2or the eigenratio λ2/λNcan remain inside the corresponding synchronization region.

It is easy to see that

i)for criterion (8), the larger the λ2, the better the network synchronizability;

ii)for criterion (9), the larger the ratio λ2/λN, namely the closer to 1, the better the network synchronizability.

To this end, it is interesting to find what kinds of network topologies might have the best possible synchronizability. To search for optimal network topologies that may have the best synchronizability, it was found [22] that, in any group of networks with same number of nodes and same number of edges, the totally homogeneous networks are optimal, better than others in the same group of networks. A totally homogeneous network is characterized by the degrees, girths and pathsums of its nodes, defined respectively as follows [22]:

i)Degree of a nodei, denoted byki, is the number of its adjacent edges.

As small-sized examples of totally homogeneous networks,those shown in Fig. 2 are respectively optimal ones from their own groups of networks with same number of nodes and same number of edges, in the sense that comparing to the other networks in the same group they have the largest λ2and λ2/λN[22].

It can be seen from Fig. 2 that all optimal totally homogeneous networks are homogeneously and symmetrically connected, with many cycles. Indeed, these are important features of optimal networks with best synchronizability observed from extensive simulations [22], [24], and verified by higher-order topologies as further discussed below.Nevertheless, this conjecture remains to be further proved mathematically.

V. EXPLORING HIGHER-ORDER TOPOLOGIES

As mentioned, cycles are important and indeed essential for having optimal network synchronizability, which are main subjects for study in algebraic topology [25]. In complex networks, their higher-order topologies involve many cycle motifs of different orders, such as cliques (fully-connected subgraphs) of different orders like triangles, tetrahedrons and so on, as well as cavities of different orders [23].

For a given network, define

m0= number of nodes,

m1= number of edges,

m2= number of triangles,

m3= number of tetrahedrons,

and so on. Then, the Euler characteristic number is computed by

χ=m0−m1+m2−m3+···

Furthermore, define

r0= 0 by convention,r1= rank of node-edge adjacency matrix (called incidence matrix in elementary graph theory),

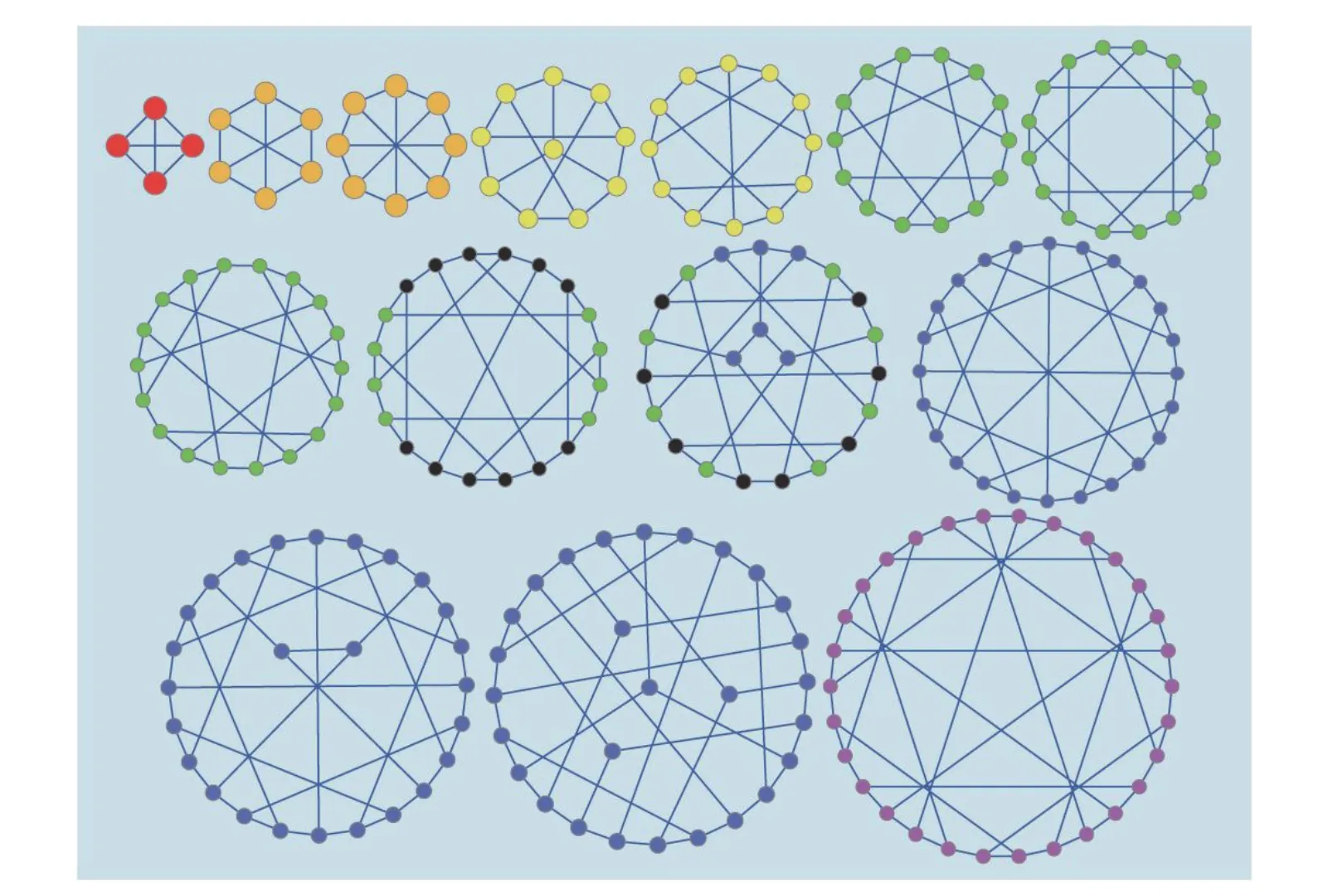
Fig. 2. Optimal totally homogeneous network examples [22].

Fig. 3. Four types of networks. From left to right: regular network, small-world network, random-graph network, totally homogeneous network [23].

r2= rank of edge-face adjacency matrix,

r3= rank of face-polyhedron adjacency matrix,and so on. Then, the Betti numbers are computed by

βk=mk−rk−rk+1,where

β0= number of 0th-order cavities (connected subgraphs,called components in elementary graph theory),

β1= number of 1st-order cavities,β2= number of 2nd-order cavities,

and so on. To this end, the Euler-Poincaré formula is given by

χ=m0−m1+m2−m3+···=β0−β1+β2−β3+···

To show how these higher-order topological characteristics could be useful for studying the network synchronizability,consider four types of comparable typical networks as an example, each with 20 nodes and 40 edges: a regular network,a small-world network, a random-graph network and a totally homogeneous network, as shown in Fig. 3 [23].

For these four types of networks, the simulation and calculation results are summarized in Table I.

It can be observed from Table I that the synchronizability of the four types of networks follows the following ordering:totally homogeneous network > random-graph network >small-world network > regular network, where > means“better than”. This ordering of synchronizability is consistent with other reports in the literature and is clearly supported bythe criterion based on λ2, as well as the Betti numbers (the bigger, the better) and the Euler characteristic number (the smaller, the better, taking into account the negative sign).

TABLE I NUMERICAL RESULTS OF FOUR TYPES OF NETWORKS [23]

It can also be seen that the eigen-ratio criterion has a little inconsistency between regular network and small-world network in this example. This seems due to the multiple synchronization region problem mentioned above [21] and the imprecise definition of a small-world network, which actually is not much different from the regular network in this example.

According to extensive simulations and observations, as those shown in Table I, the Euler characteristic number appears to be the best criterion to be used for determining the network synchronizability. Since the Euler characteristic numbers are integers, they clearly differ from each other by integers, while eigenvalues differ from each other only in decimals that could be difficult to distinguish in some cases.

VI. CONCLUSIONS

This article presents an overview on the state-of-the-art development in the studies of complex network synchronization, and discusses the progress in searching for best possible network topologies with optimal synchronizability. It reports the finding of the key roles of homogeneous structures and cycle components in enhancing the network synchronizability, especially the most recent recognition of Euler characteristic numbers or Betti numbers as a reliable measure for the optimal synchronizability, using which best network topologies can be clearly identified.

Higher-order topologies, and generally algebraic topology theory [25], provide powerful and effective tools for in-depth investigation of complex network dynamics such as diffusion,synchronization, spreading and evolution [26], as also discussed recently in [27]–[34], which should be further explored. In particular, higher-order cycles are important to study for their key roles in supporting the optimal network synchronizability [35], [36].