基于灰色马尔可夫模型的器材故障预测研究

黄俊超， 胡 勇（空军勤务学院，江苏 徐州 221000）

0 引 言

飞机飞行训练强度大、难度高，对航空器材的可靠性要求高。器材故障会降低飞机的出动率，进而直接影响飞行部队战斗力。因此做好器材故障预测显得十分重要。器材故障预测能够提前预测到系统的运行状态即将发生的故障，可以通过对预测结果的分析，提前做好预防准备以避免或减少故障带来的损失，节省大量人力物力，相比于故障诊断具有前瞻性。

目前对于飞机器材故障预测的研究取得了许多成果，常见的基于数据驱动的预测技术有时间序列分析法、人工神经网络预测法、基于滤波器的预测法及灰色理论预测法。诸多研究表明，将不同模型进行有机组合能够充分发挥各自优势，提高预测精度，因此本文提出将灰色GM（ 1,1）模型与马尔可夫模型相结合的预测方法。

1 灰色马尔可夫组合模型的建立

灰色理论是把进行预测的系统看做一个灰色系统，然后使用微分方程模型求解预测结果。其中的灰色GM（ 1,1）模型有计算简便、对原始数据需求量少、不需要考虑影响因素等特点，比较适合于预测规律性相对明确的参数，对具有指数变化趋势的参数具有较好的预测精度。但是对于器材故障数据这类波动频率、随机性都比较大的数据序列的预测精度较差，无法对历史数据中的有用信息进行充分提取。

然而相对比于灰色GM（ 1,1）模型，马尔可夫模型预测过程能够通过状态转移概率矩阵来展现系统潜在的规律，从而描述具有随机性的动态过程。因此将上述两个模型相结合，采用灰色预测模型来揭示器材故障发生的总体趋势，然后采用马尔可夫链来体现状态与状态间的转换规律，就可以有效改善器材故障这类波动性较强的数据的预测效果。

1.1 建立灰色GM（ 1,1）模型

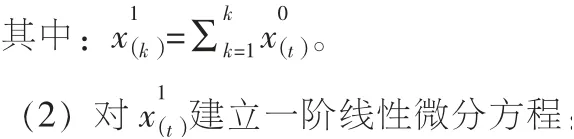
（3）运用最小二乘法，求得、，得到微分方程：

1.2 建立灰色马尔可夫模型

（1）首先进行状态区间划分

根据灰色GM（ 1,1）模型所展现出的故障时间点变化的总体趋势，以实际故障时间点与GM（ 1,1）模型预测值的相对比值的取值范围为依据，将等长划分为个状态区间：

（2）构建步状态转移矩阵

设系统状态集合为｛,,…,E｝，（）表示由状态E经过步转移到状态E的概率，则：

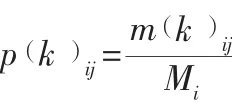
其中：（）为原始数据经过步由状态E转移到状态E的次数；M为状态出现的次数。

记步状态转移概率矩阵为（），则：

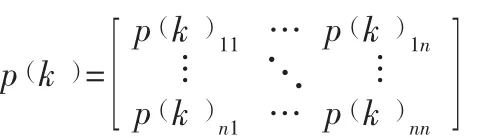
（3）计算灰色马尔可夫预测值

灰色马尔可夫预测值：

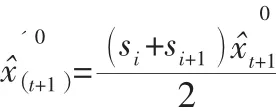
2 实例分析

本文以30台主油泵装机后发生故障的时间点作为研究对象，根据前27台主油泵故障时间点，对最后3台油泵的故障时间点进行预测，并于实际故障时间点进行对比，以检验模型预测效果。原始数据见表1故障时间。

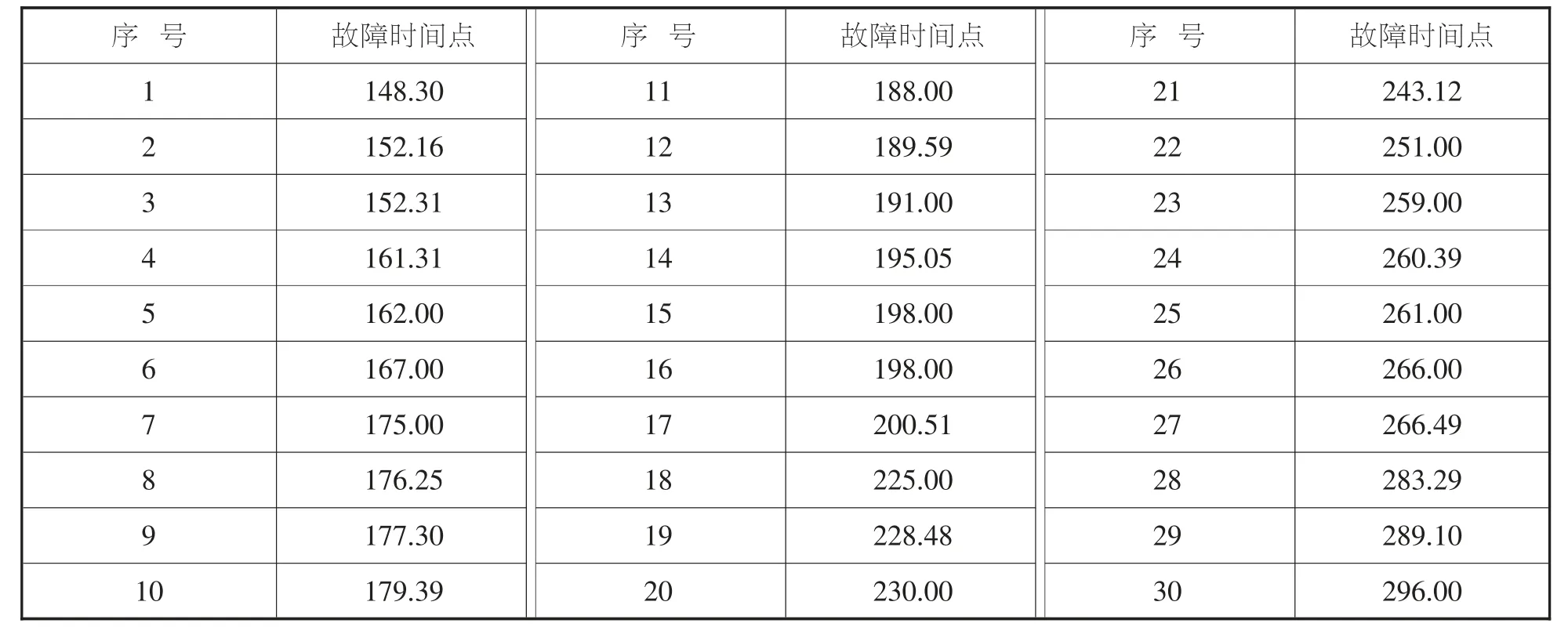
表1 故障时间点

2.1 进行灰色GM（ 1,1）模型预测

首先建立原始序列：

表2 灰色预测结果

2.2 进行灰色马尔可夫模型预测

（1）确定状态区间

故障发生实际时间点与GM（ 1,1）模型预测值的相对比值的取值范围为=［0.9 6,1.08 ］，等长度划分为四个区间，则各个状态对应的区间分布如表3所示：

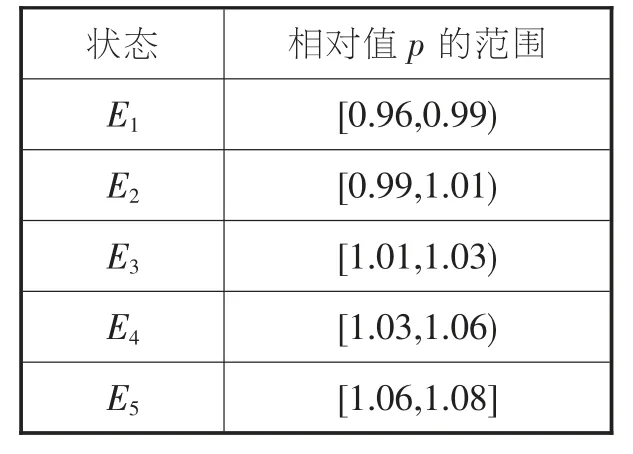
表3 状态区间

（2）计算状态转移概率矩阵

分别计算出（≤ 4）步转移矩阵：

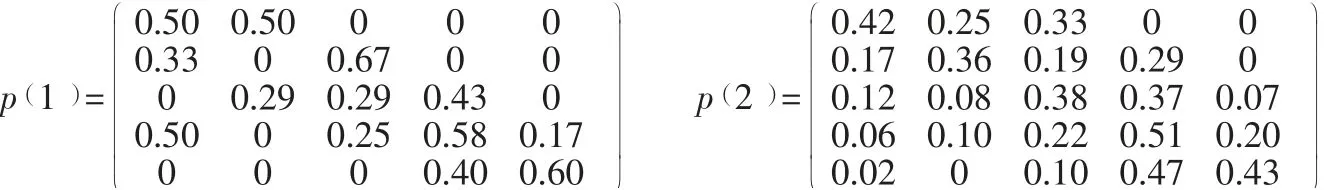
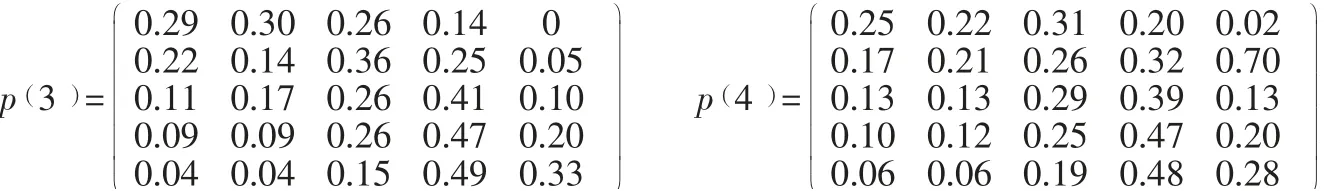
以28号数据为例进行预测，状态转移区间预测过程如表4所示：

表4 状态转移预测计算表

剩余两组数据以同样方法进行预测，得到最终预测结果见表5。

表5 最终预测结果

2.3 预测精度判定

将预测值与实际值进行比对，计算出相对误差分布如表6所示。

表6 预测结果对比

可视化对比如图1所示。

图1

可以明显看出，灰色马尔可夫预测结果相对误差极小，说明该模型对油泵故障时间点有很好的预测效果，可以为实际工作提供参考。

3 结束语

本文根据油泵故障时间点的原始数据，建立了基于灰色马尔可夫模型的器材故障预测模型，实例分析表明该模型能够很大程度上降低预测误差，具有很好的预测效果。在实际工作中，可以通过对预测结果的分析，提前做好预防措施以及维修准备，有效提高飞机保障效益。