不同材料延性断裂韧性与裂尖拘束的关联及其影响因素分析
2022-04-14赵家鑫王国珍涂善东轩福贞
赵家鑫,王国珍,涂善东,轩福贞
(华东理工大学 承压系统与安全教育部重点实验室,上海 200237)
0 引言
目前,含缺陷结构的断裂预测和安全评定主要采用基于断裂力学的方法,材料的断裂韧性是一个重要的输入参数[1]。大量研究[2-4]表明,断裂韧性受试样或结构几何、裂纹尺寸、加载方式和材料性能的影响,这种影响一般称为裂尖拘束效应,其本质是结构对材料裂尖塑性变形的阻碍。裂尖拘束的增加导致裂尖正应力和三轴应力的增大(断裂驱动力增大),从而使材料的断裂韧性降低。材料的断裂韧性测试一般使用标准平面应变高拘束试样,而实际结构中裂纹的拘束一般较低。由于标准试样和结构裂纹拘束的不匹配,导致断裂评定的不准确性。为提高评定的精度,需要考虑裂尖拘束对材料断裂韧性的影响。为此需要研究建立材料断裂韧性与裂尖拘束的定量关联,采用拘束修正的断裂韧性进行结构断裂评定[3-4]。
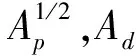
本文基于文献中大量不同几何和尺寸试样(不同面内/面外拘束)的延性断裂韧性试验数据,结合有限元计算,研究不同材料延性断裂韧性和统一拘束参数Ad之间的关联,并采用数值模拟的方法,分析研究材料力学性能参数对关联线的影响。
1 试样材料、几何尺寸与断裂韧性
为建立材料延性断裂韧性与统一拘束参数Ad的关联线,本文收集了文献[14,17-22]中不同材料、不同几何和裂纹尺寸试样的延性断裂韧性数据。试验材料主要为合金钢,包括X90[17],X80[18],20MnMoNi55[19],A508[14],40H[20],16MND5[21]和TP304[22]。表1示出了这些材料的力学性能参数,其中40H-A和40H-B钢的回火温度分别为450,680 ℃[20],TP304-A和TP304-B钢的试验温度分别为93,288 ℃[22]。
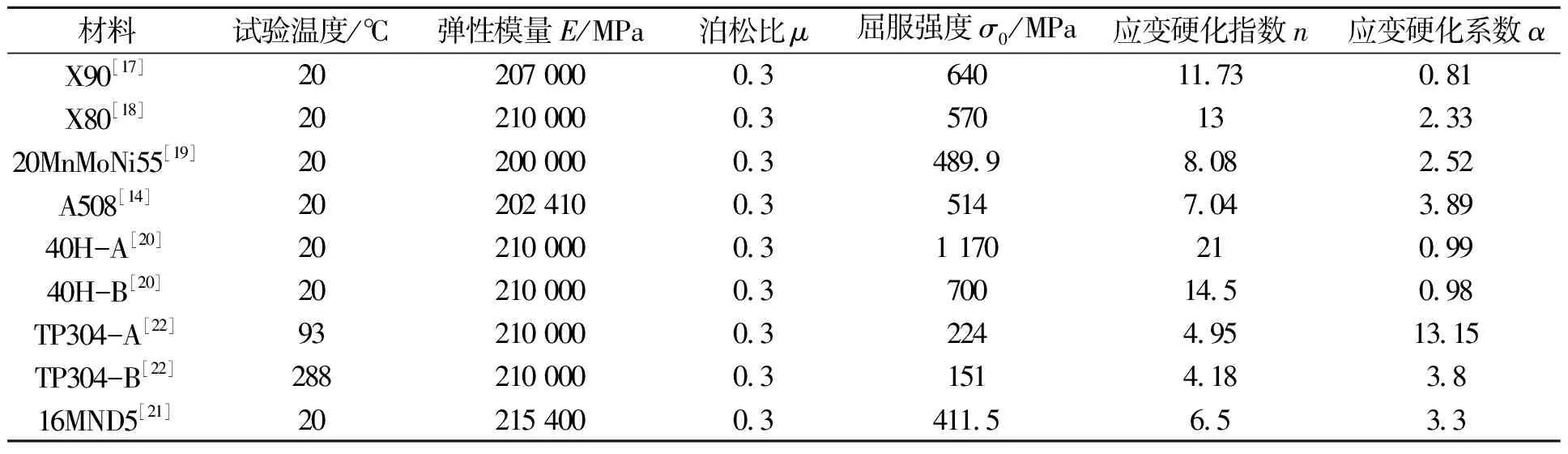
表1 材料力学性能参数Tab.1 Mechanical property parameters of the materials
表2示出了所有材料的试样几何尺寸、断裂韧性和拘束参数Ad值。试样主要包括单边缺口拉伸(SEN(T))试样和单边缺口弯曲(SEN(B))试样。所有试样的延性断裂韧性值Jc通过文献[14,17-22]中的试验或数值模拟的J-R阻力曲线获得。
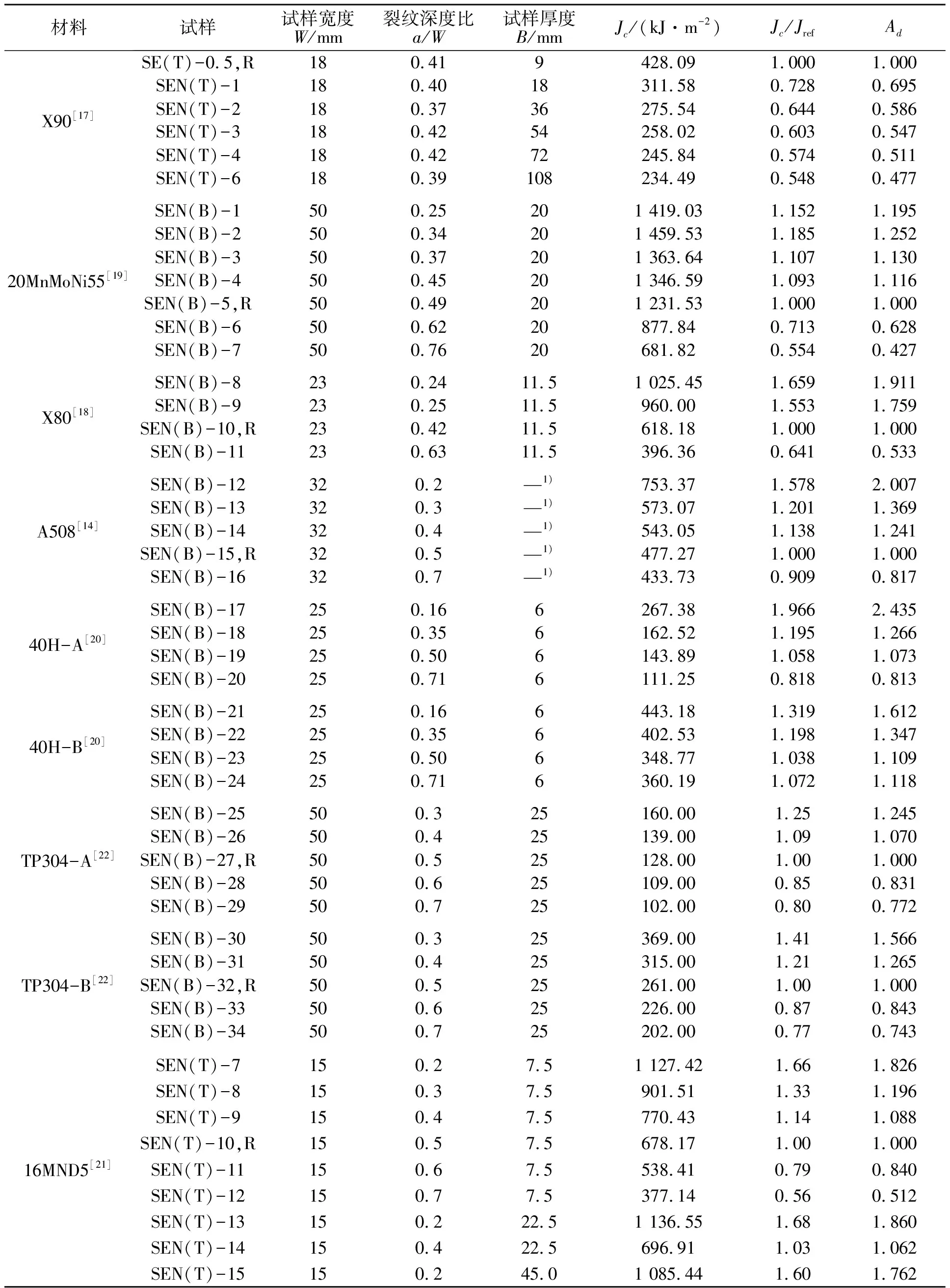
表2 不同材料试样的几何类型、尺寸、断裂韧性与拘束参数值Tab.2 The geometry types,sizes,fracture toughness and constraint parameters for specimens of different materials
2 统一拘束参数Ad
基于CTOD的统一拘束参数Ad[14]的定义如下:
Ad=δ/δref
(1)
式中,δ为试样或结构裂纹的CTOD值;δref为标准高拘束参考试样在断裂时的CTOD值。
对于不同的断裂韧性试样,用有限元法可以计算得到其断裂时的δ值,从而用式(1)可计算得到Ad值,并可以构建标称断裂韧性Jc/Jref与Ad间的统一关联线[14]。随着Ad值的增大(拘束降低),材料断裂韧性提高[14]。在工程结构的断裂预测和评定中,Jc/Jref-Ad关联线可用来获得材料拘束相关的断裂韧性。
3 统一拘束参数Ad的有限元计算方法
为了建立断裂韧性与统一拘束参数Ad的关联,对表2中不同试样的Ad值通过Abaqus软件[23]建立的三维试样有限元模型进行计算。典型的SEN(T)和SEN(B)试样的有限元模型如图1所示。由于试样几何结构与载荷的对称性,只建立1/4模型进行有限元分析。在SEN(T)试样端面上施加均匀分布的力载荷,在SEN(B)试样中心刚体上施加竖直向下的位移载荷。所有有限元模型网格均采用三维8节点网格(C3D8R)。为了提高模型非线性迭代的收敛性,模型裂尖采用根半径r0=2.5 μm的钝化裂尖,裂纹尖端区域采用聚焦环网格(图1(c))。采用表1中的材料力学参数进行有限元计算。
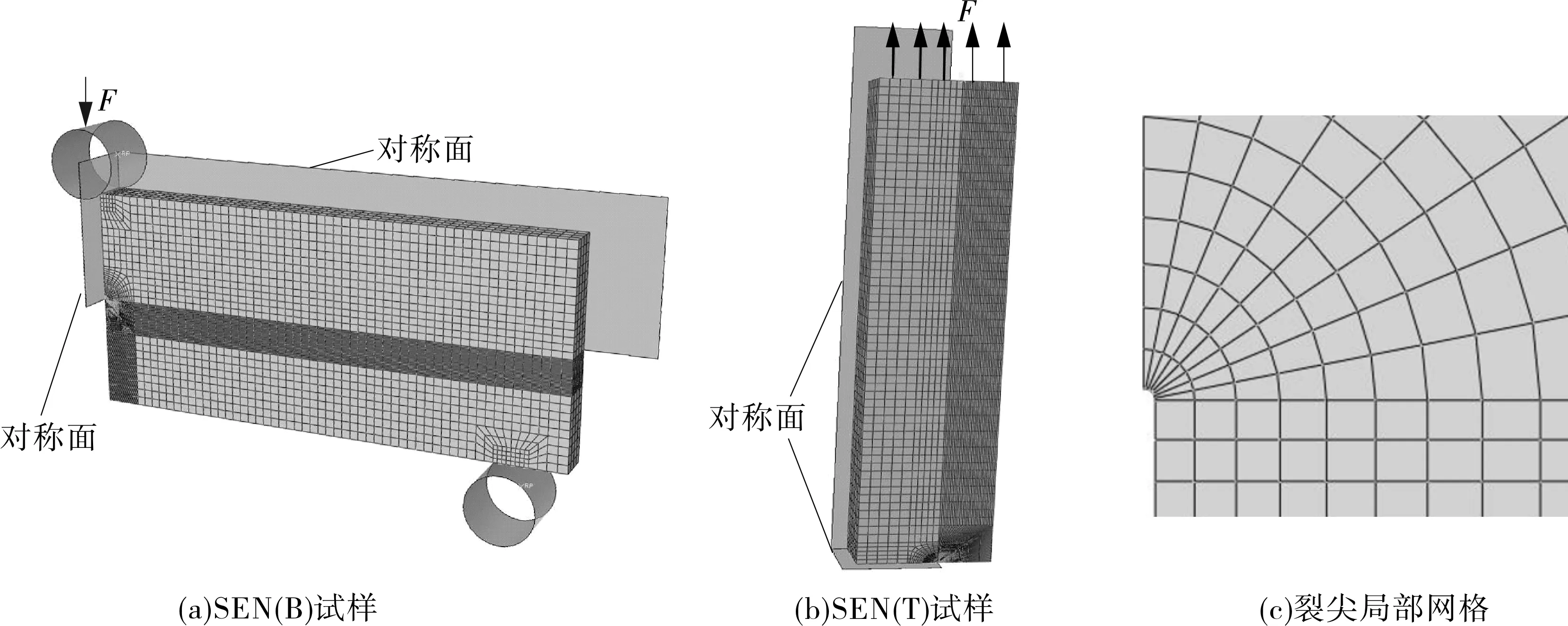
图1 SEN(B)试样和SEN(T)试样的三维有限元模型和裂尖局部网格
统一拘束参数Ad采用式(1)计算。式(1)中的CTOD在有限元计算中采用90°相交线法确定,即从裂尖引出两条互成直角且对称的直线,两直线与裂纹两边交点间的距离即为CTOD[14]。表2中标有R的标准高拘束试样取为参考试样,取试样厚度方向在断裂韧性Jc下的平均CTOD作为试样的δ和δref值,代入式(1)计算Ad值,计算结果列于表2。表2中40H和TP304钢的Ad数据来源于文献[20,22]。
4 延性断裂韧性与统一拘束参数Ad的关联
用表2中的数据建立材料断裂韧性与统一拘束参数Ad的关联。图2示出不同材料的标称断裂韧性Jc/Jref与参数Ad的关联线,其中Jref是标准参考试样的断裂韧性。在构建不同材料的Jc/Jref-Ad关联线时,关联线上每个数据点均为相应试样在各自断裂韧性Jc下的Ad值,此时通过式(1)可知Ad的分子为相应试样裂纹尖端J积分达到Jc时裂尖的CTOD值。对于同种材料的关联线,不同试样的Ad会存在分散,这主要源于各试样断裂韧性Jc的分散性。
从图2可看出,每一种材料都对应唯一一条Jc/Jref-Ad关联直线,且断裂韧性Jc/Jref都随Ad的增加(拘束的减小)而线性增加。对于标准参考试样,Jc/Jref与Ad值均为1,因此每一条直线都通过交点(1,1)。图2中的所有Jc/Jref-Ad关联直线的方程可以用下式表达:
Jc/Jref=aAd+b
(2)
式(2)中的系数a和b可以通过对图2中的数据点进行线性拟合得到。拟合的每种材料的系数a和b见表3。图2中9种材料的Jc/Jref-Ad关联直线及式(2)的关联方程可用于基于J-Ad二参数法纳入统一拘束的结构断裂预测和评定中[16,20]。在工程应用时,将结构裂纹的Ad值代入式(2)可以计算得到材料拘束修正的断裂韧性值,用该值进行评定,可提高评定精度[16,20]。
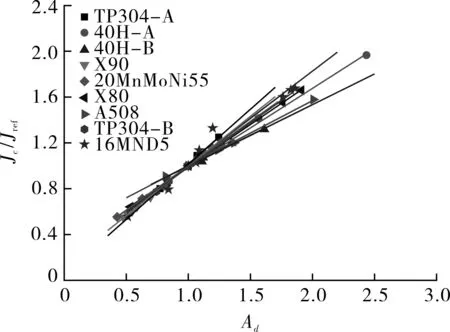
图2 不同材料的标称断裂韧性Jc/Jref和统一拘束 参数Ad的关联线Fig.2 The correlation lines between the normalized fracture toughness Jc/Jref and Ad of different materials
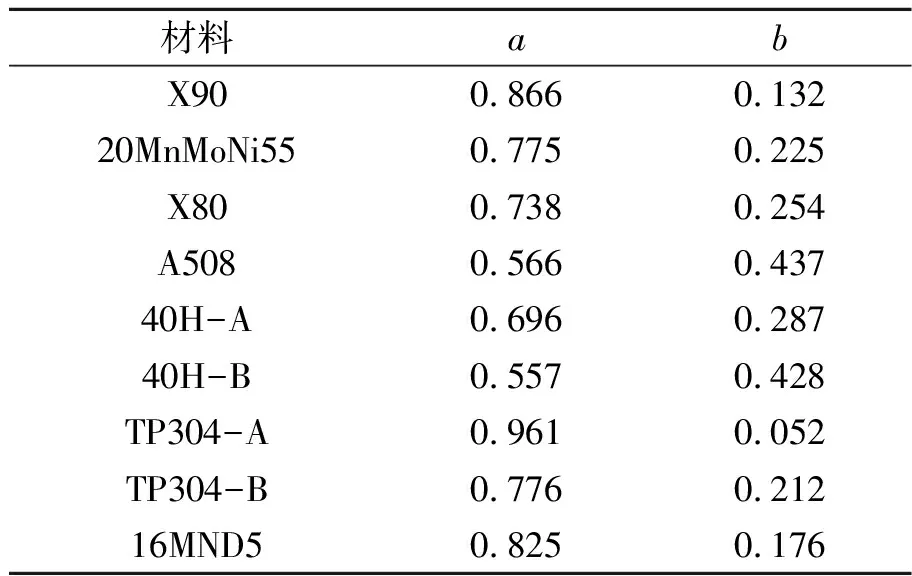
表3 不同材料Jc/Jref-Ad关联方程式(2)中的系数a,b值Tab.3 Constants a and b in the Jc/Jref-Ad correlation equation (Eq.(2)) for different materials
式(2)中的系数a是Jc/Jref-Ad关联线的斜率,其值的大小反映了材料断裂韧性对拘束的敏感性。较高的a值表明材料的断裂韧性对拘束较敏感。表3中的数据表明,TP304-A和X90钢的断裂韧性对拘束的敏感性较高(较高的a值);20MnMoNi55,X80,TP304-B和40H-A钢的断裂韧性对拘束的敏感性适中(中等的a值);A508钢和40H-B钢的断裂韧性对拘束的敏感性较低(较低的a值)。不同材料的断裂韧性对拘束的敏感性不同,可能源于它们不同的力学性能和断裂特性。力学性能的差异主要体现在表1中不同材料的屈服强度和硬化指数的不同,断裂特性的差异主要与微细观断裂机制的不同相关。力学性能和断裂特性对材料断裂韧性与拘束关联的影响(即对拘束敏感性的影响)将在下一节进行深入研究。
5 影响Jc/Jref-Ad关联线的因素分析
为了定量地理解影响Jc/Jref-Ad关联线的材料力学性能和断裂特性因素。本节基于GTN(Gurson-Tvergaard-Needleman)延性损伤模型的数值模拟方法,研究材料力学性能参数(应变硬化指数和屈服强度)和断裂特性参数对Jc/Jref-Ad关联线的影响。
5.1 基于GTN损伤力学模型的延性断裂模拟方法
合金钢延性断裂的微观机理包括微孔洞的形成、长大和聚合三个阶段。GTN损伤力学模型描述了这一延性断裂机理,是广泛使用的、基于有限元法模拟材料延性断裂的损伤力学模型[24-25]。其已成功用于模拟不同试样[26]和含裂纹结构[24](如管道,压力容器等)的延性断裂模拟和分析。在笔者研究组的前期工作中[13,25],已采用嵌入GTN模型的有限元方法模拟得到了不同几何尺寸A508钢试样的J-R阻力曲线,并用试验结果进行了验证。GTN模型及对材料延性断裂模拟的有限元方法在文献[24-26]中有较为详细的介绍。本文采用该方法,研究材料力学性能和断裂特性参数对Jc/Jref-Ad关联线的影响。
GTN模型中有9个参数,分为三类。第一类是3个本构参数q1,q2,q3;第二类为孔洞形核参数,包括材料初始孔洞体积分数f0、孔洞形核体积分数fN、孔洞形核平均应变εN和孔洞形核率标准差SN;第三类是临界孔洞参数,包括孔洞聚合临界体积分数fc和断裂临界孔洞体积分数fF。本文以A508钢作为基础研究材料,其GTN模型参数在前期工作中已标定得到[25]。其中模型本构参数q1=1.5,q2=1,q3=2.25;孔洞形核参数f0=0.000 2,fN=0.002,εN=0.3,SN=0.1;临界孔洞参数fc=0.04和fF=0.17。
采用二维平面应变SEN(B)试样模型(如图3(a)所示)进行研究,试样宽度W=32 mm,裂纹深度比a/W= 0.2,0.3,0.4,0.5,0.7(改变试样拘束水平),裂纹扩展区网格尺寸为0.1 mm[25](见图3(b))。用嵌含有GTN模型的Abaqus[23]有限元软件模拟SEN(B)试样的J-R阻力曲线,通过0.2 mm钝化线法测得材料的延性断裂韧性Jc。
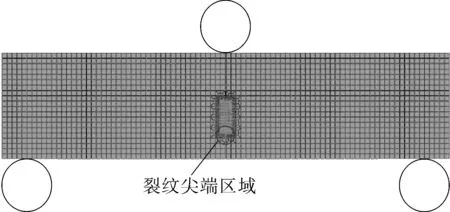
(a)二维平面应变SEN(B)试样
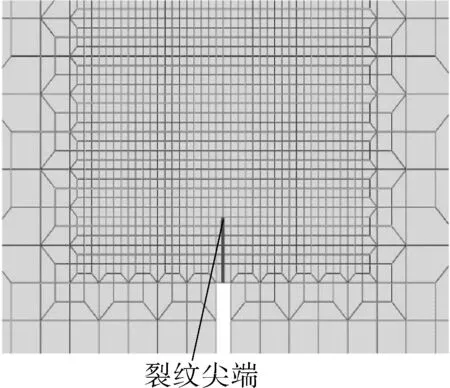
(b)裂纹扩展区网格图3 基于GTN模型模拟延性裂纹扩展的二维平面应变 SEN(B)试样的有限元模型(a/W=0.2,W=32 mm)和 裂纹扩展区网格Fig.3 Typical 2D SEN(B) finite element model(a/W=0.2, W=32mm) and meshes in crack growth area for ductile crack growth simulation based on GTN model
5.2 应变硬化指数n对Jc/Jref-Ad关联线的影响
为探究应变硬化指数n对Jc/Jref-Ad关联线的影响,保持A508钢的屈服强度σ0和GTN模型参数不变,参数化改变材料硬化指数n,n的取值范围(n=3~12)覆盖大部分金属材料,其中n=7.04相应于A508钢的硬化指数值。对不同n值下不同裂纹深度比a/W的SEN(B)试样的J-R曲线进行了模拟。图4示出a/W=0.2和0.7的两个典型试样的不同n值下的J-R曲线,表明n对深裂纹(a/W=0.7)的J-R阻力曲线有更大影响。当裂纹扩展量较小时,较低n值的J-R曲线较高;当裂纹扩展量较大时,较高n值的J-R曲线较高。n值对J-R曲线的影响与材料硬化对裂尖应力状态的影响及其随裂纹扩展的变化有关。不同n值下每一SEN(B)试样的延性断裂韧性Jc通过在其J-R曲线上用0.2 mm钝化线法测量得到。为了计算不同n值下每一SEN(B)试样的拘束参数Ad值,用二维平面应变SEN(B)试样的准静态有限元模型计算J-CTOD关系。图5示出不同n值下两个典型SEN(B)试样的J-CTOD关系曲线。随着n值增大,J-CTOD关系曲线斜率增大。采用a/W=0.5的SEN(B)试样作为标准参考试样(其断裂韧性值为Jref),通过J-CTOD关系曲线和式(1),可以计算得到每一SEN(B)试样在断裂J积分Jc下的拘束参数Ad值。
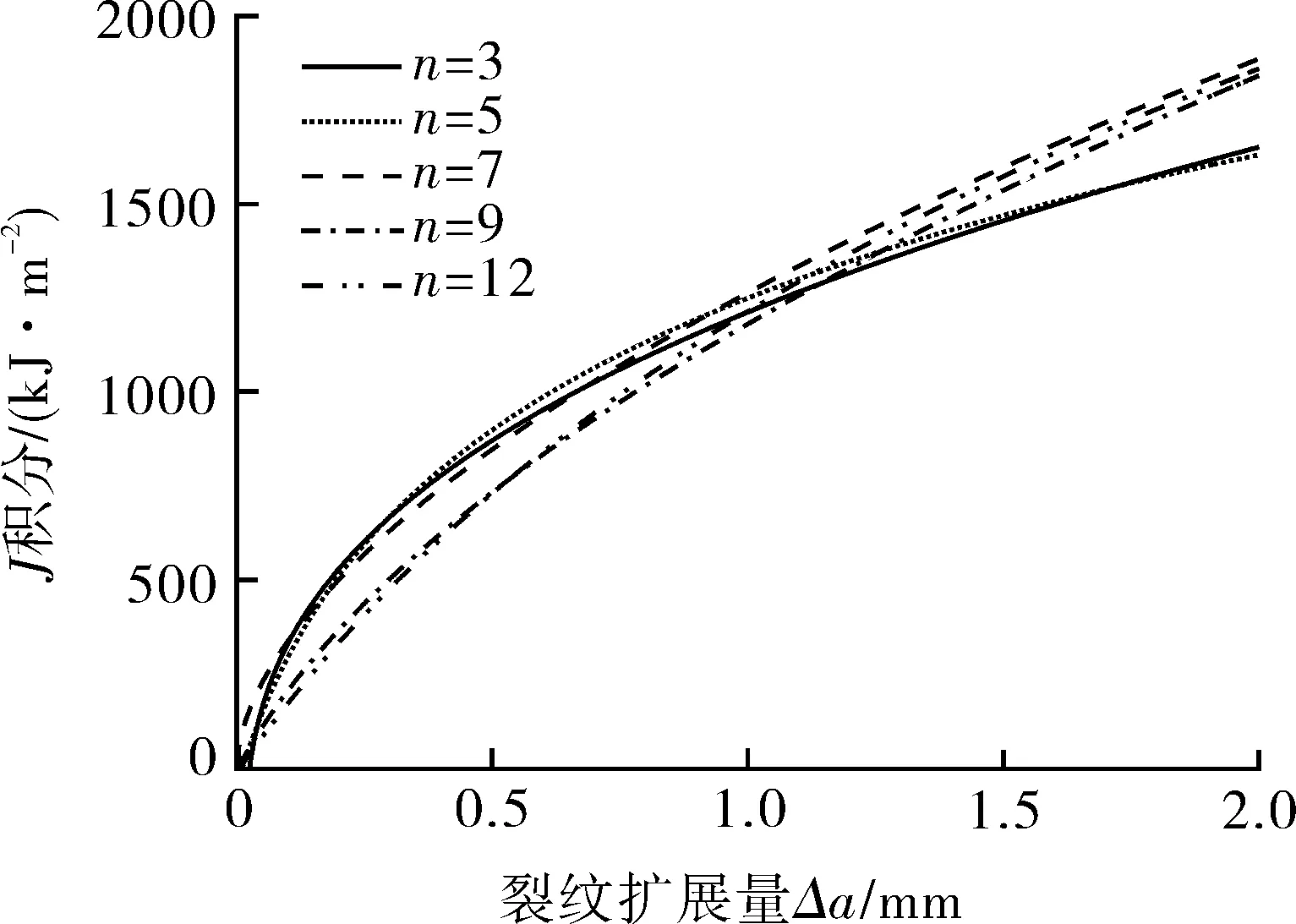
(a)a/W=0.2
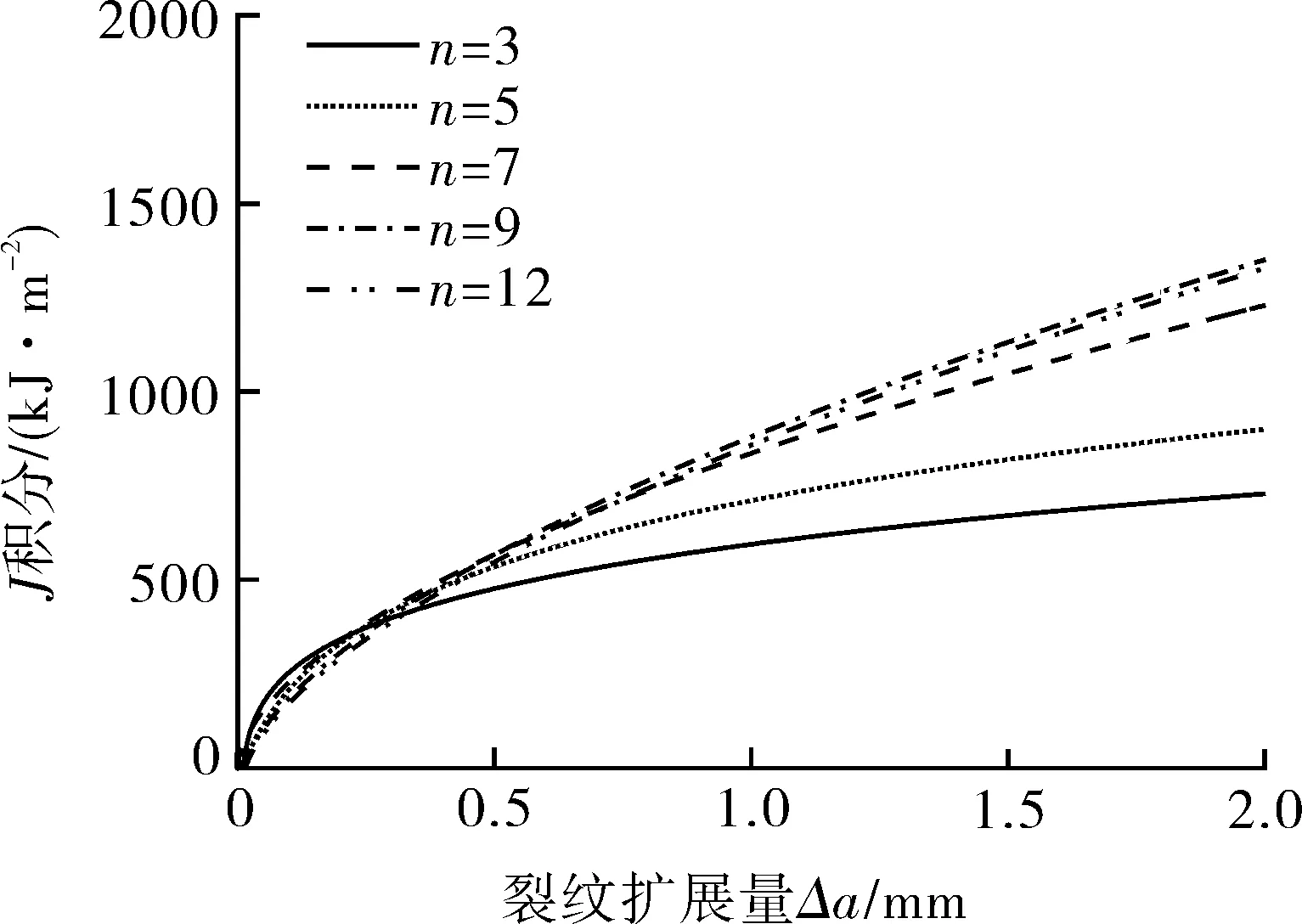
(b)a/W=0.7图4 基于GTN模型模拟得到的不同n值材料的 典型试样a/W=0.2和a/W=0.7的J-R阻力曲线Fig.4 The J-R resistance curves simulated based on GTN model for typical specimens with a/W=0.2 and a/W=0.7 for the materials with different n
按上述方法计算得到不同试样的Jc/Jref与Ad值以后,便可获得不同n下的Jc/Jref-Ad关联线,如图6所示,可以看出,n对关联线的斜率有显著影响。不同n值下,依照式(2)中的Jc/Jref-Ad关联方程拟合的系数a和b值列于表4。
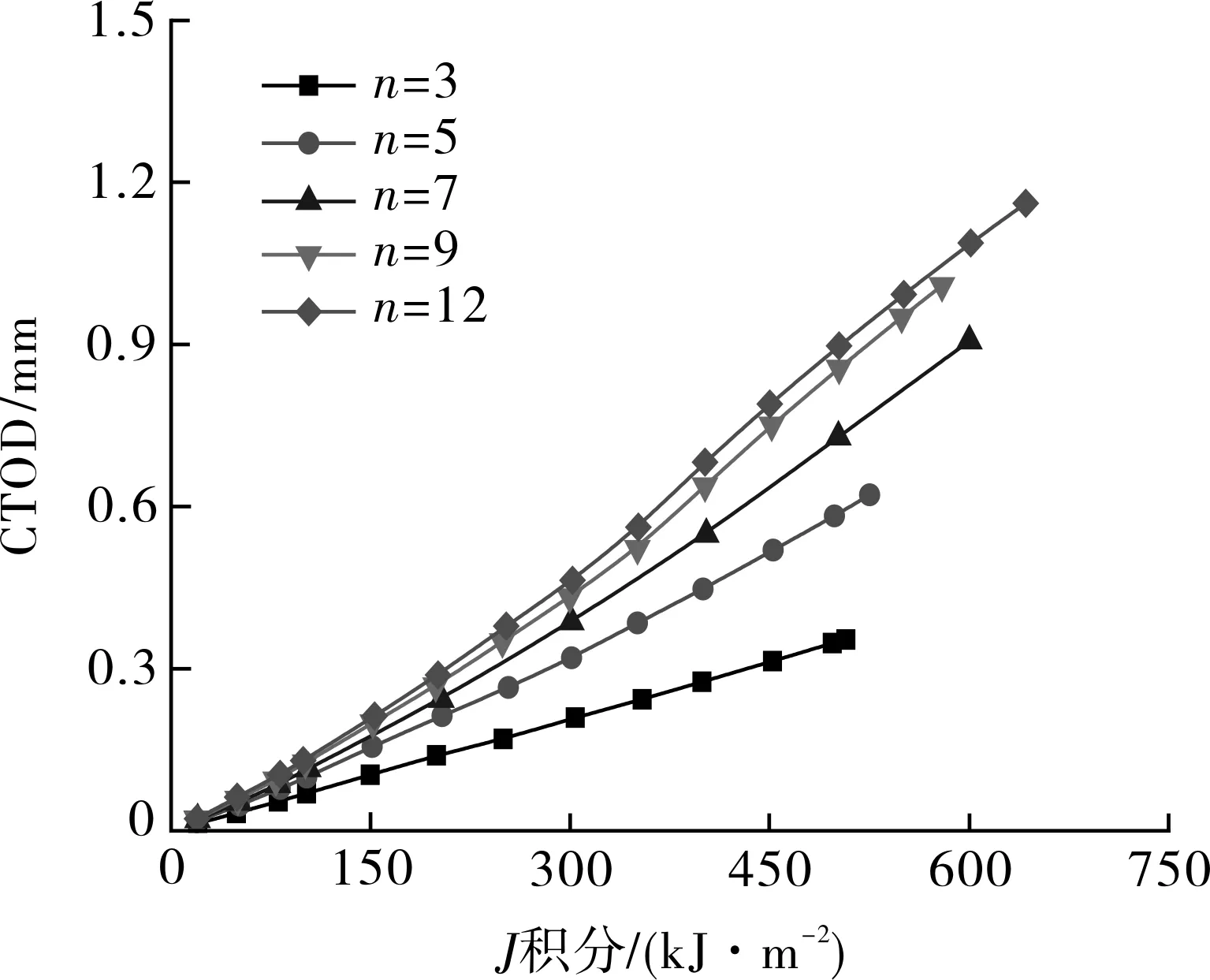
(a)a/W=0.2
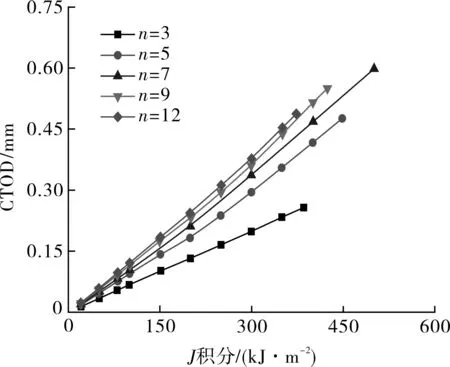
(b)a/W=0.7图5 典型试样a/W=0.2和a/W=0.7在不同n下的 CTOD随J积分的变化Fig.5 Change of CTOD with J-integral for typical specimens with a/W=0.2 and a/W=0.7 for the materials with different n
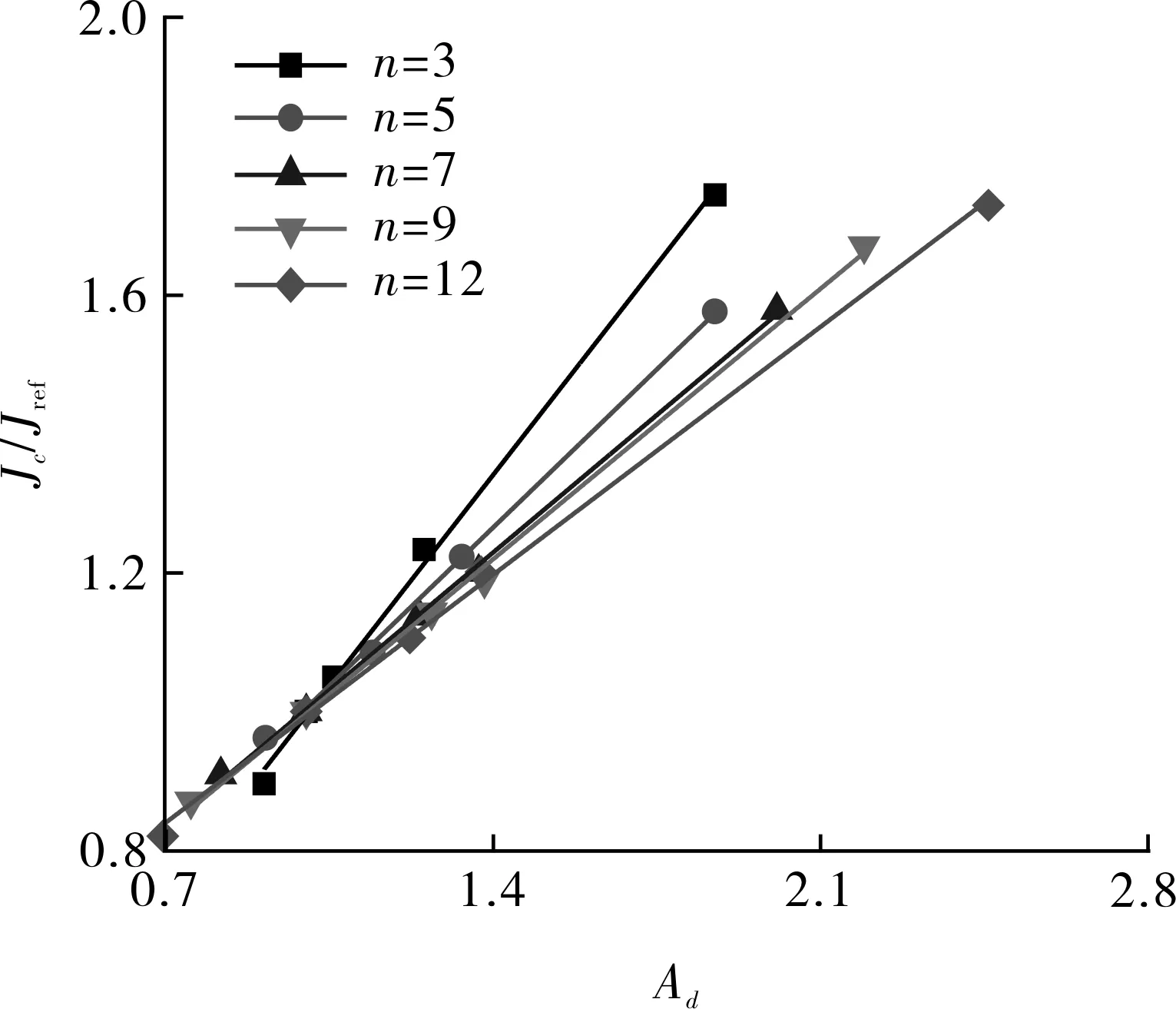
图6 不同n值材料的Jc/Jref-Ad关联线Fig.6 The Jc/Jref- Ad correlation lines for the materials with different n
由图6和表4中的数据表明,随着n的减小(材料应变硬化能力提高),关联线斜率升高(a值增大)。这说明n值低的材料的断裂韧性对拘束的变化敏感。这一结果与文献[27]中基于三轴应力的拘束分析基本一致。因此图2中TP304钢斜率大的原因可能主要源于其较低的n值(见表1),40H钢斜率小的原因可能主要源于其较高的n值(见表1)。对于n值较小的材料,其应变硬化能力强,当裂尖拘束发生较小变化时,其裂尖应力和应力三轴度可能发生较大变化,这将会导致材料断裂韧性Jc发生较大变化。因此,对于n值较小的材料,由于其断裂韧性对拘束比较敏感,在结构断裂预测和评定中应特别需要考虑拘束效应的影响。
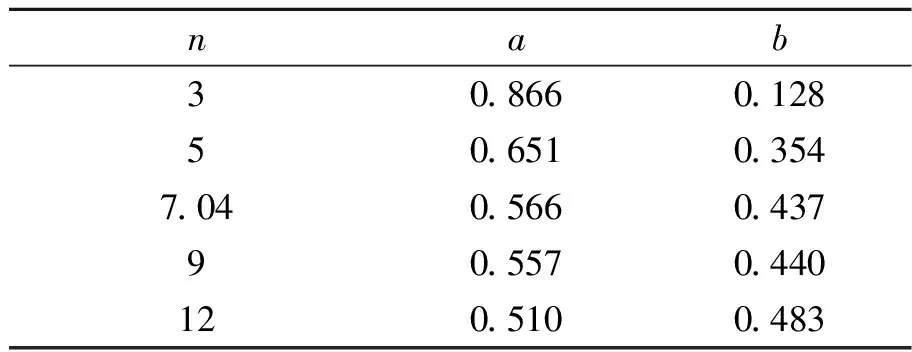
表4 不同n值材料Jc/Jref-Ad关联方程(式(2))的系数a,b值Tab.4 Constants a and b in the Jc/Jref-Ad correlation equation (Eq.(2)) for the materials with different n
5.3 材料屈服强度σ0对Jc/Jref-Ad关联线的影响
为探究材料屈服强度对Jc/Jref-Ad关联线的影响,保持A508的硬化指数(n=7.04)与GTN模型参数不变,参数化改变材料的屈服强度σ0(以A508钢的σ0= 514 MPa为基值,每隔200 MPa改变σ0),使σ0的取值范围(σ0=314~1 114 MPa)覆盖大部分金属材料。对不同σ0的不同裂纹深度比a/W的SEN(B)试样的J-R阻力曲线进行了模拟,图7示出两个典型试样(a/W=0.2和0.5)的阻力曲线,表明随着σ0增大,J-R曲线升高。不同σ0值下每一SEN(B)试样的延性断裂韧性Jc通过在其J-R曲线上用0.2 mm钝化线法测量得到。为了计算不同σ0值下每一SEN(B)试样的拘束参数Ad值,用二维平面应变SEN(B)试样的准静态有限元模型计算J-CTOD的关系。图8示出不同σ0值下两个典型SEN(B)试样的J-CTOD关系曲线。随着σ0值减小,J-CTOD关系线斜率增大。采用a/W=0.5的SEN(B)试样作为标准参考试样(其断裂韧性值为Jref),通过J-CTOD关系线和式(1),可以计算得到每一SEN(B)试样在断裂J积分Jc下的拘束参数Ad值。
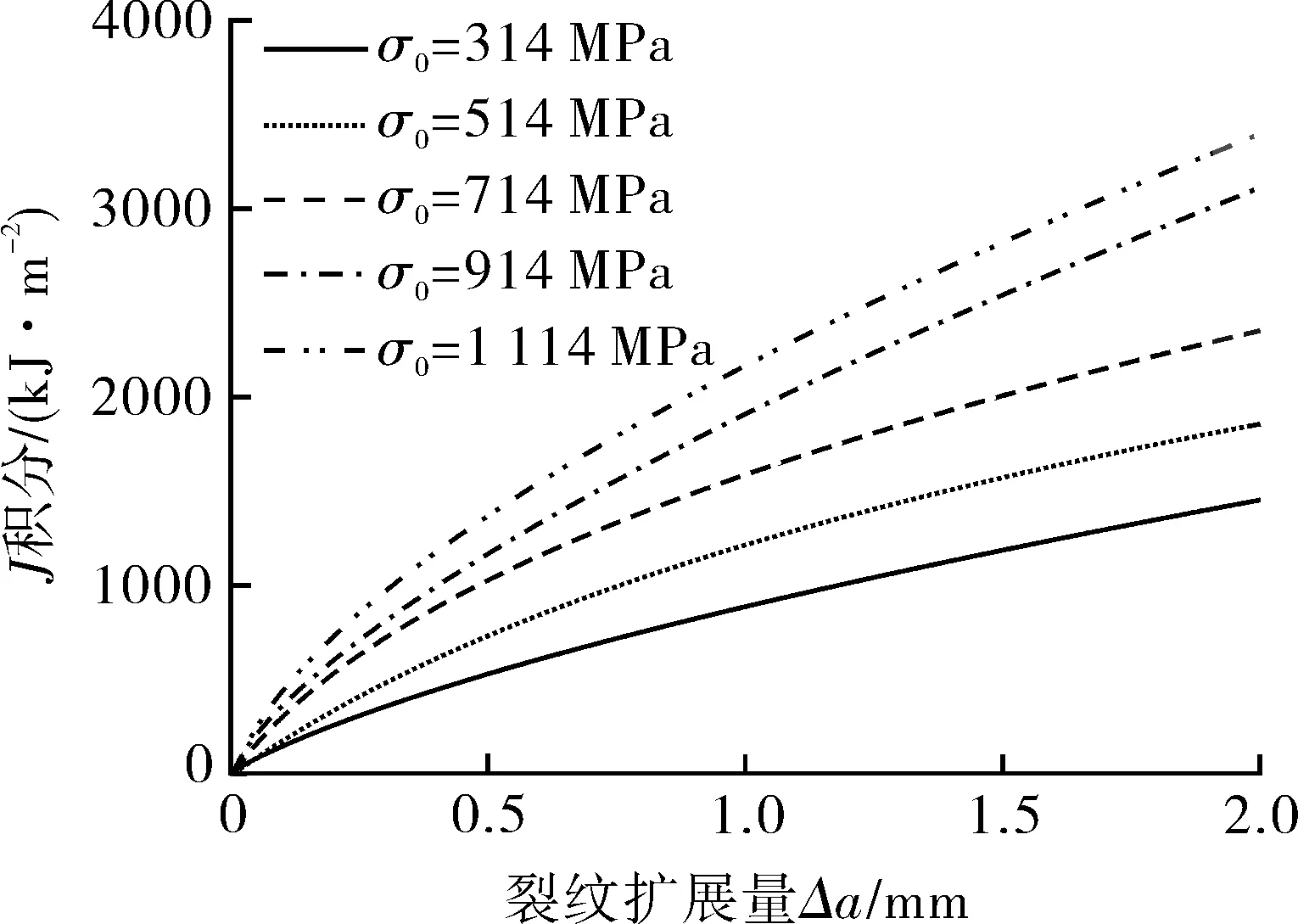
(a)a/W=0.2
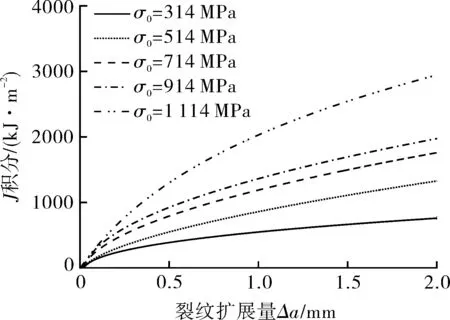
(b)a/W=0.5
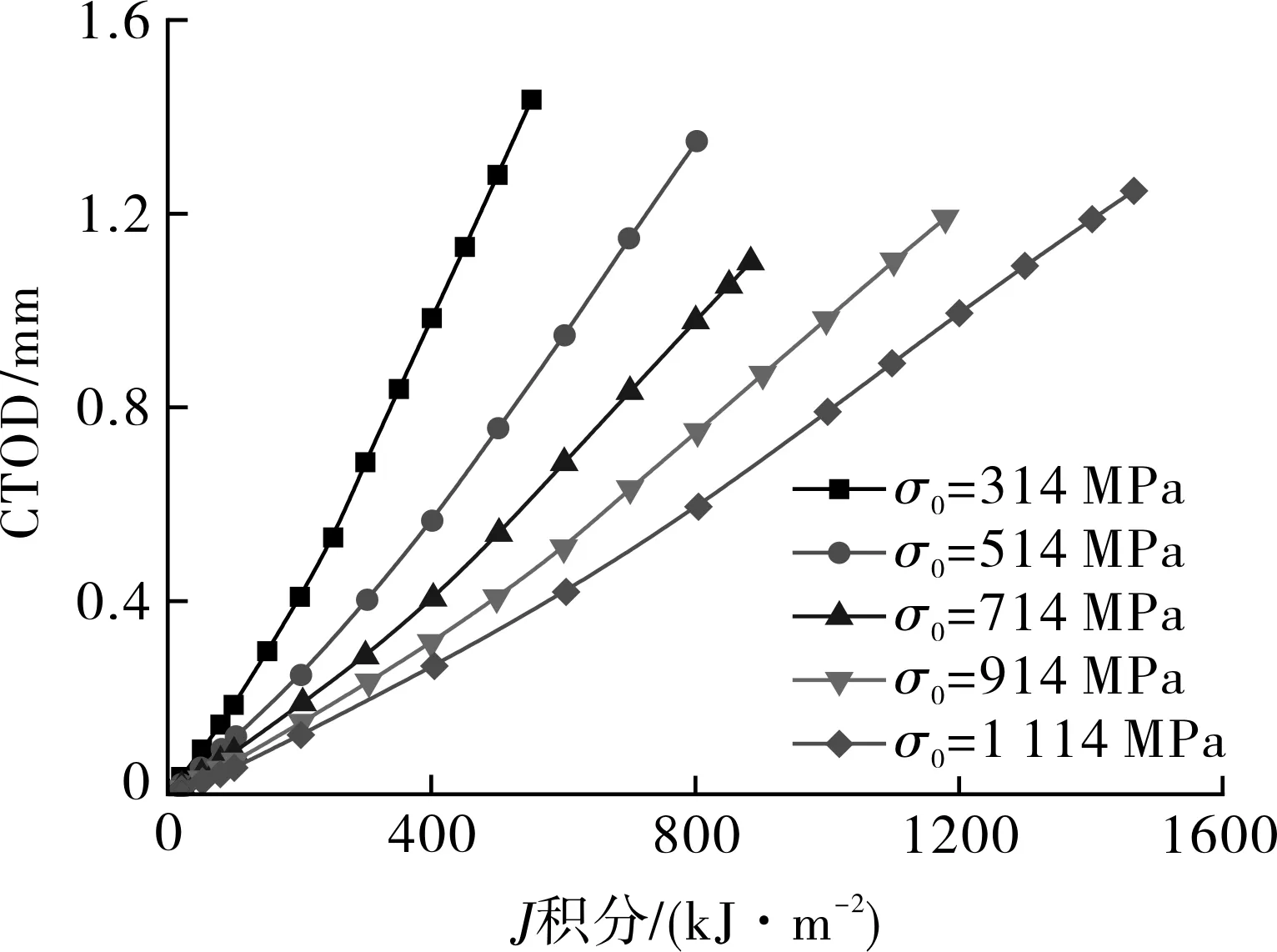
(a)a/W=0.2 (b)a/W=0.5图8 不同屈服强度σ0下典型试样的CTOD随J积分的变化Fig.8 Change of CTOD with J-integral for typical specimens under different yield strength σ0
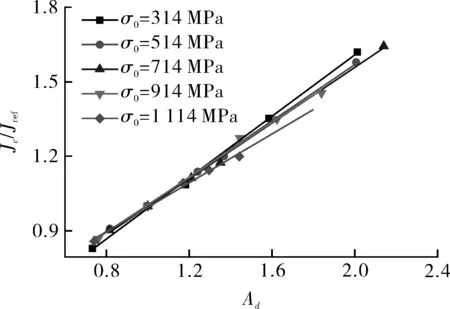
图9 不同屈服强度σ0下材料的Jc/Jref-Ad关联线
for the materials with different yield strengthσ0
基于Jc/Jref与Ad值,获得的不同σ0下的Jc/Jref-Ad关联线,如图9所示。图中显示σ0对关联线的斜率影响较小,不同σ0下Jc/Jref-Ad关联方程(式(2))拟合的系数a和b值列于表5中。图9和表5表明,随着σ0的减小,关联线的斜率(a值)略有增大,这说明σ0较低的材料,其断裂韧性对拘束较为敏感。
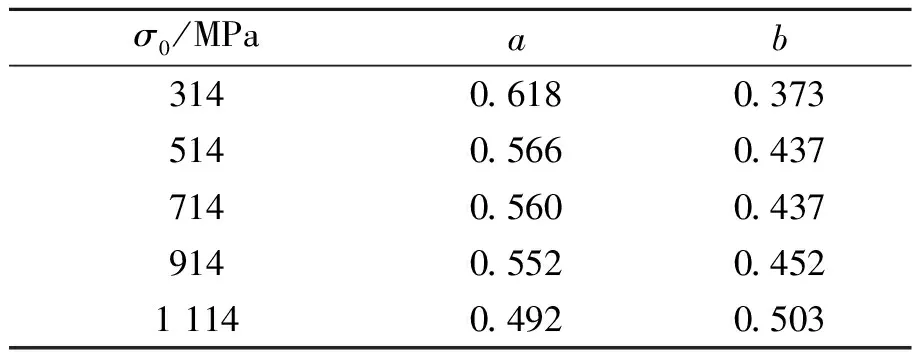
表5 不同屈服强度σ0下Jc/Jref-Ad关联方程(式(2))的系数a,b值Tab.5 Constants a and b in the Jc/Jref-Ad correlation equation (Eq.(2)) for the materials with different yield strength σ0
5.4 材料断裂特性对Jc/Jref-Ad关联线的影响
初始孔洞体积分数f0是GTN模型的参数之一。材料的延性断裂韧性随着f0的增加而降低,因此可通过改变f0来改变材料的断裂特性。为探究材料断裂特性对Jc/Jref-Ad关联线的影响,保持A508钢的真应力-应变曲线和其余GTN模型参数不变,参数化改变f0。由于材料的延性断裂韧性对很低的f0值的变化不太敏感,f0值在A508钢的最小(f0=0.000 2)的基础上放大100倍得到最大值(f0=0.02)。因此f0的取值范围为f0=0.000 2~0.02,以得到较宽范围变化的材料延性断裂韧性。图10示出有限元模拟的a/W=0.2和0.5的两个典型试样在不同f0值下的J-R曲线,表明随着f0的增大,J-R阻力曲线降低(材料断裂阻力降低)。每个试样的断裂韧性Jc和拘束参数Ad的计算方法同5.2节。图11示出不同f0下材料的Jc/Jref-Ad关联线,关联线斜率随着f0的增大而增大,这表明断裂阻力较低的材料的断裂韧性对拘束的变化较敏感。拟合得到的不同f0下材料的Jc/Jref-Ad关联方程(式(2))的系数a,b数值列于表6。由图11和表6表明,当f0发生较大变化时,关联线斜率(a值)变化并不很大,这表明材料断裂特性对Jc/Jref-Ad关联线的影响不显著。
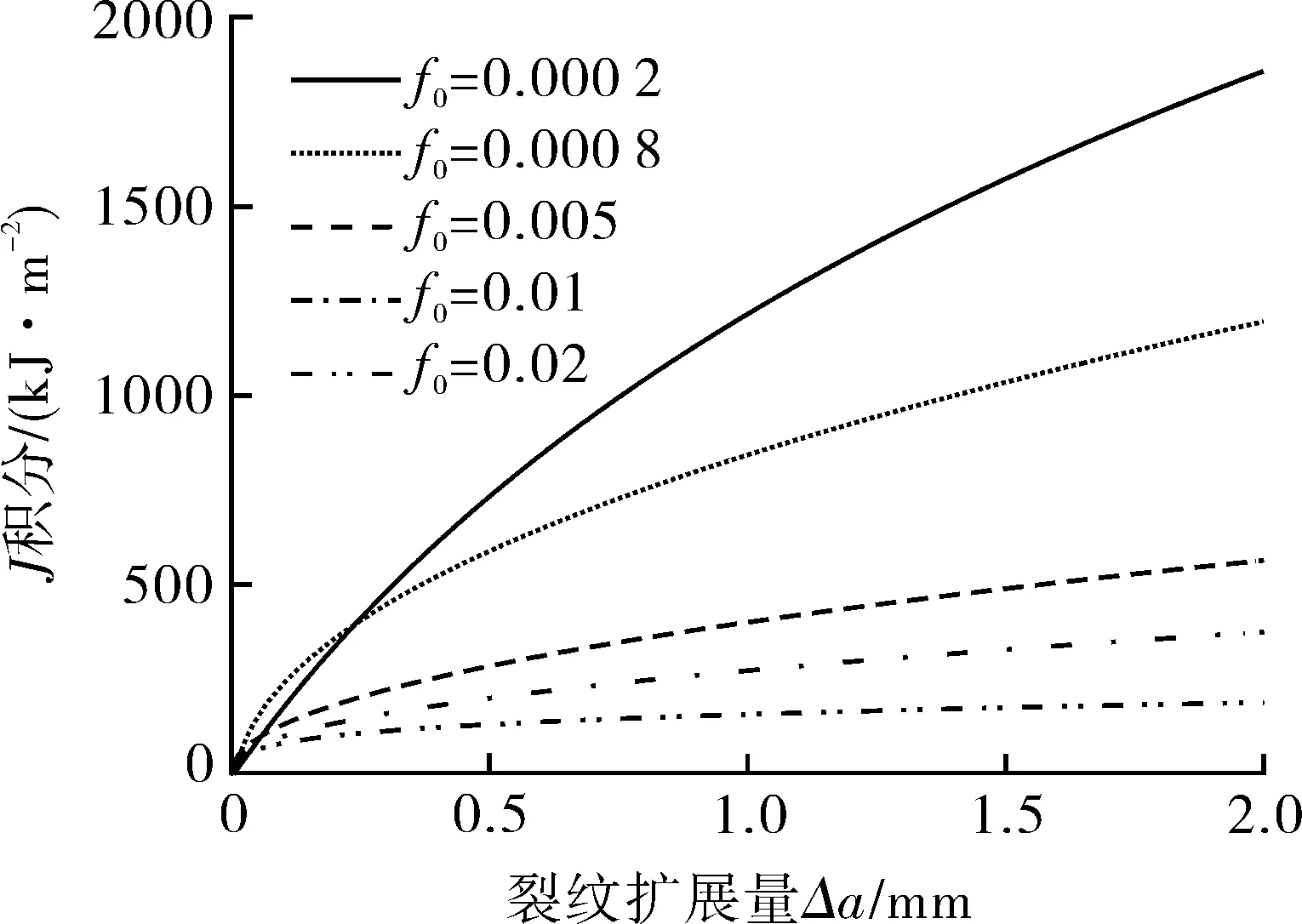
(a)a/W=0.2
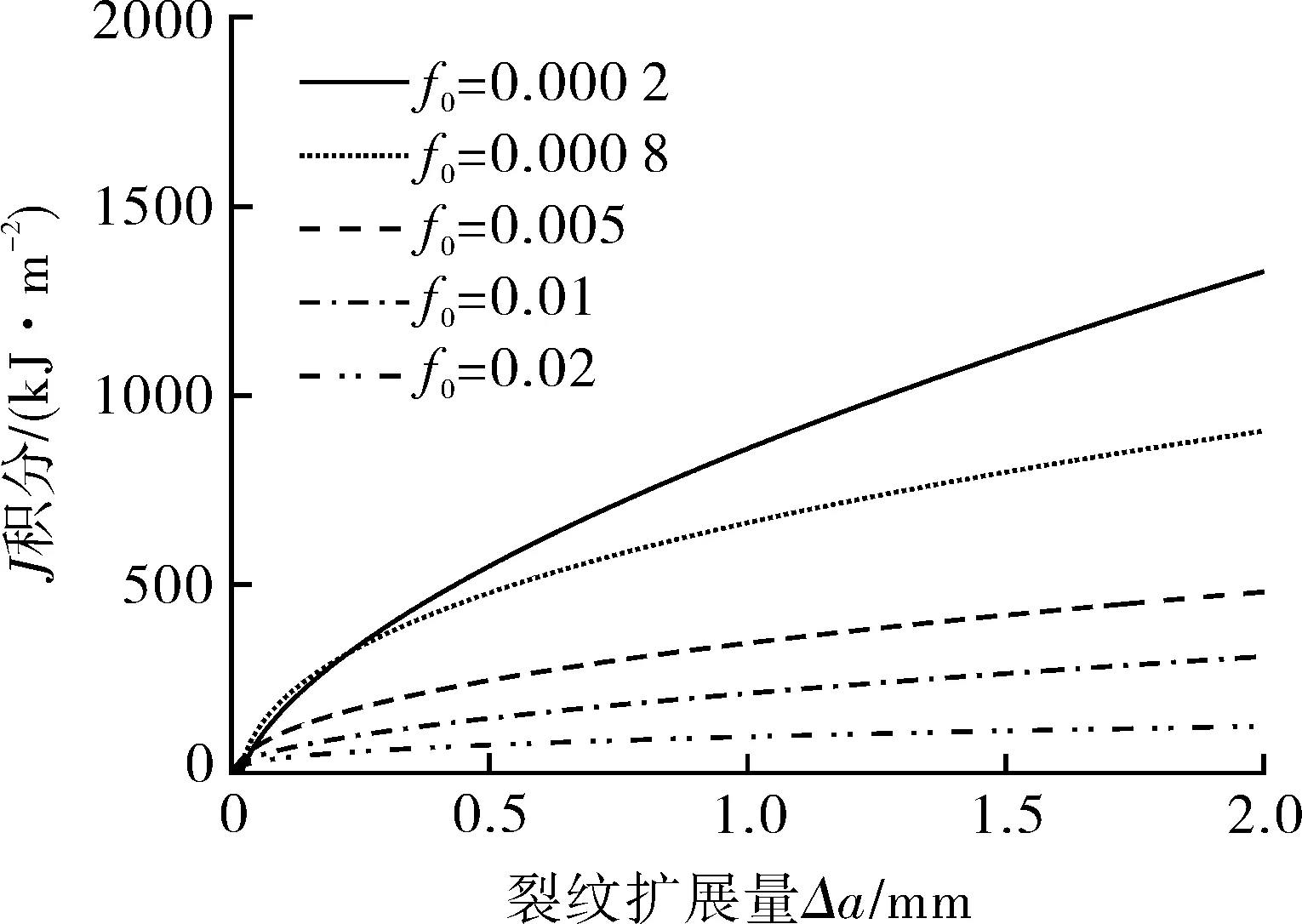
(b)a/W=0.5图10 不同f0下典型试样的J-R阻力曲线Fig.10 The J-R resistance curves of typical specimens for materials with different f0
上述第5.2~5.4节的结果比较表明:n对Jc/Jref-Ad关联线斜率的影响最大;初始孔洞体积分数f0的影响次之;屈服强度σ0的影响最小。低硬化指数n,低屈服强度σ0和高f0(低断裂阻力)的材料的延性断裂韧性对裂尖拘束的变化比较敏感。对于这类材料的结构,在断裂预测和评定中要着重考虑裂尖拘束对断裂韧性的影响。图2中不同材料延性断裂韧性对拘束敏感性的不同的原因应当是硬化指数、屈服强度和断裂特性三者综合影响的结果。
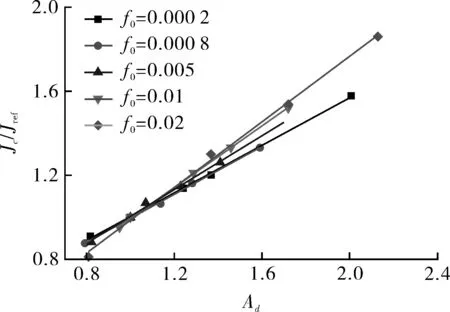
图11 不同f0下材料的Jc/Jref-Ad关联线Fig.11 The Jc/Jref-Adcorrelation lines for the materials with different f0
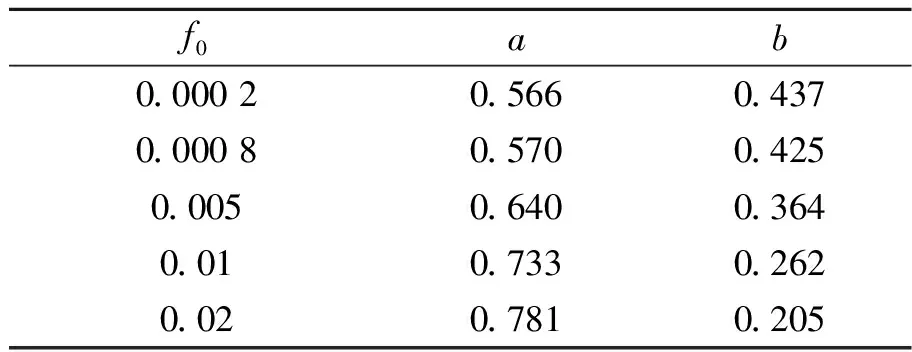
表6 不同f0下材料Jc/Jref-Ad关联方程(式(2))的拟合系数a,b值 Tab.6 Constants a and b in the Jc/Jref-Adcorrelation equation (Eq.(2)) for the materials with different f0
6 结论
(1)不同材料、不同几何尺寸试样的标称化延性断裂韧性Jc/Jref与统一拘束参数Ad之间呈线性关系。随拘束的降低(Ad值增大),材料断裂韧性增大。得到了不同材料的Jc/Jref-Ad关联方程,其可用于基于J-Ad二参数法纳入统一拘束的结构断裂预测和评定中。
(2)影响材料Jc/Jref-Ad关联线的主要因素包括材料的应变硬化指数n,屈服强度σ0和断裂特性(以参数f0表征的断裂阻力)。其中n对Jc/Jref-Ad关联线斜率的影响最大;f0的影响次之;屈服强度σ0的影响最小。
(3)低硬化指数n,低断裂阻力f0和低屈服强度σ0的材料的延性断裂韧性对裂尖拘束的变化较敏感。对于这类材料的结构,在断裂预测和评定中要着重考虑裂尖拘束对断裂韧性的影响。
