一种低复杂度的仿射投影算法

杨海斌

（湖南理工职业技术学院，湘潭 411004）

0 引言

自适应滤波在通信、控制、雷达、声学回声消除等许多领域都有应用。稀疏性是信号或信道参数中普遍存在的特性。遗憾的是，传统的自适应滤波算法，如最小均方（LMS）、归一化LMS（NLMS）和仿射投影算法都没有利用信号或信道模型中的稀疏性来提高学习性能。然而，利用信道的稀疏性可以显著提高学习过程的收敛速度或稳态性能。因此，在经典算法中引入了许多改进来利用稀疏性。一个著名的利用稀疏性的算法族是比例算法族，另一种著名的利用稀疏性的策略是将惩罚函数加入到传统算法的代价函数中，但这些方法中加入了一些常规算法，从而增加了算法的计算量。

本文采用了不同于在比例算法族中加入一些特征的方法，而是考虑到回声信道的稀疏脉冲响应包含几个能量很高的系数，而且大部分系数都接近于零。因此，利用一些关于小系数不确定性的知识，可以将小于假定不确定性的系数用零代替，以降低计算代价。除了上述利用稀疏性的方法外，还利用集员滤波技术，提出了低复杂度的仿射投影算法。当误差小于预定门限时，集员滤波策略避免了新的更新，从而进一步降低了计算量。

1 集员滤波

在集员滤波中，令Ω表示所有感兴趣的“输入-期望”数据对(,)的集合，用可行集Θ表示(,)属于Ω时，所有使输出误差幅度在门限内的系数矢量∈R 构成的集合，故Θ可表示为：

此外，定义包含所有权向量的约束集()，使得在给定的迭代时，其误差的大小以为上界，即

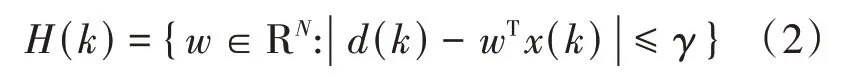
其中()，()分别为输入向量和期望信号。另定义资格集合()为()，=0,1,2,…,的交集，即：

当→时，资格集合收敛到可行集。然而，由于实际问题，我们无法计算()；但通过约束集()可得到的信息计算一个点估计值。

2 低复杂度的仿射投影算法

仿射投影算法权向量更新过程描述如下：

其中为正则化因子，是为防止被零除引入的很小的常数，是步长，称为仿射投影算法阶数，()为由个输入信号向量()组成，()=()-()为误差信号，()、()分别为维×1误差向量和期望信号，当集员滤波运用到仿射投影算法中时，则利用（）式中的后个约束集来实现，此时（）式可写成：

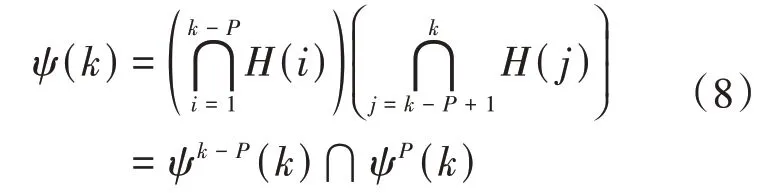
式中，ψ()表示前-个约束集的交集，ψ()表示后个约束集的交集。并定义门限向量()∈R，即：

为利用回声信道稀疏性，定义丢弃函数f:R→R为：

其中为正常数。当输出估计误差大于门限时，即 |(-)|= |()-()(-)|>γ(),=0,1,…,-1时，低复杂度的仿射投影算法更新绝对值大于的自适应系数。优化准则为：

并且受制于约束条件:

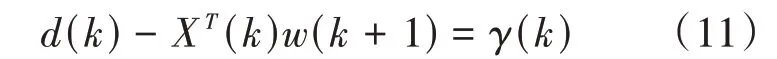
为了计算该优化问题的解，使用拉格朗日乘子方法得到

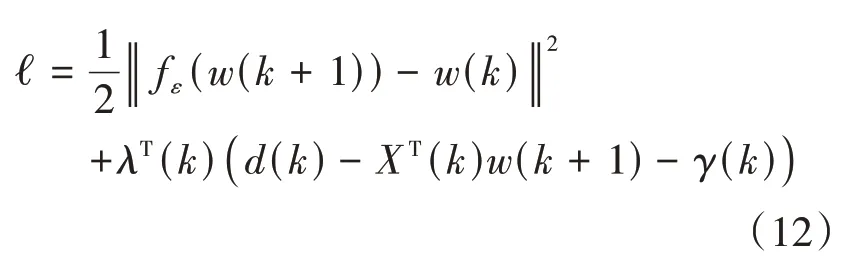
其中()=[()()…λ()]是拉格朗日乘子。取上述方程关于(+1)的梯度，令其等于零，得到

其中，F((+1))是f((+1))的雅可比矩阵，为了形成递推，利用投影近似子空间跟踪紧缩方法，将F((+1))和f((+1))分别用(+1)和F(())替换。得到

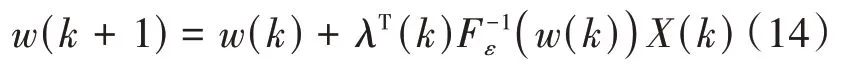
将此方程代入约束关系（11），得到()为

然后，将（10）代入（9），得到如下递推规则

其中，=2,…,

则：

其中：=[1 00]为×1维向量。

于是得到低复杂度的仿射投影算法如下：

其中：

3 仿真

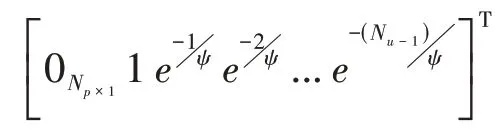
图1 稀疏路径脉冲响应，ψ=8

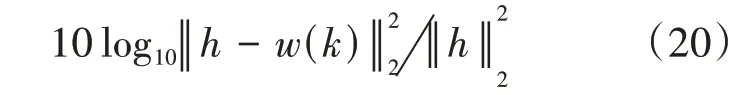
图2和图3分别给出了信噪比为20 dB和30 dB时三种算法归一化失调收敛曲线，从图中可看出，由于LCSM-APA算法和APA算法利用了过去3次迭代时的输入信号向量，加快了LCSM-NLMS算法的收敛速度。LCSM-APA算法具有与APA算法相似的性能，但其计算复杂度低。

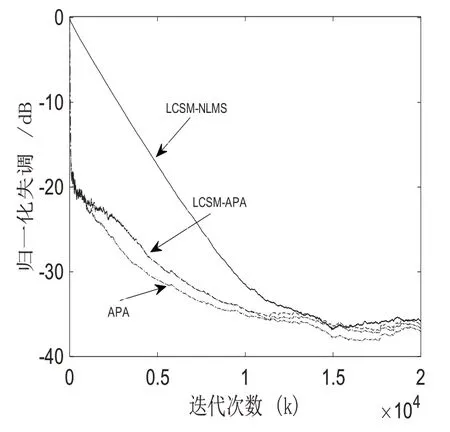
图2 新算法与相关算法收敛性能比较（SNR=20 dB）

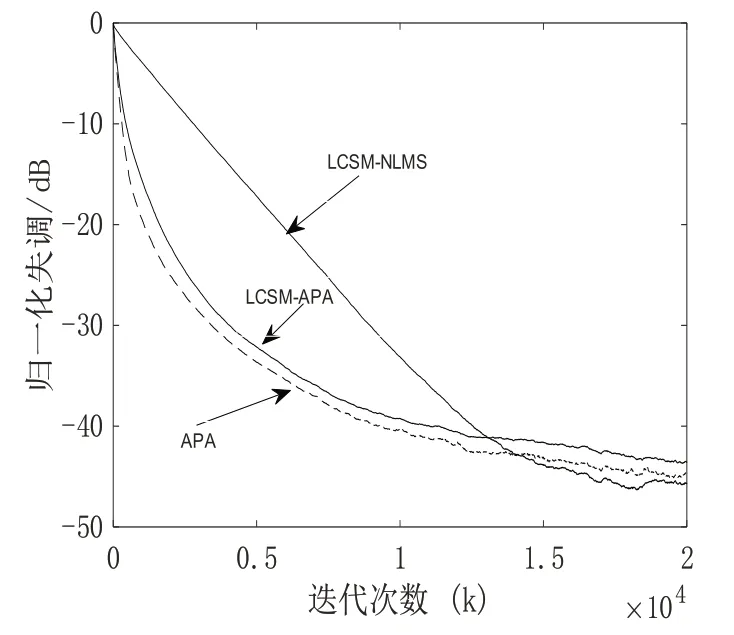
图3 新算法与相关算法收敛性能比较（SNR=30 d B）

4 结语

本文提出了一种新的低复杂度仿射投影算法，所提算法考虑到回声信道的稀疏脉冲响应包含几个能量很高的系数，而且大部分系数都接近于零。因此，利用一些关于小系数不确定性的知识，可以将小于假定不确定性的系数用零代替，以降低计算代价。此外，该方法还与集合成员技术结合，以达到更低的计算负担和更低的更新率。数值仿真结果表明，新的低复杂度仿射投影算法在计算资源方面优于仿射投影算法，且由于新算法利用了过去迭代时的输入信号向量，加快了基于集员技术的低复杂度NLMS算法的收敛速度。