热毛细液层非模态稳定性分析*
2022-04-13郑晟胡开鑫
郑晟 胡开鑫
(宁波大学机械工程与力学学院力学系 宁波 315211)
0 引言
热毛细对流是由液体表面温差引起表面张力梯度驱动的流动,是空间等微重力条件下流体的主要运动形式,广泛存在于微流控[1,2]、熔焊[3]、薄膜镀层[4]等工业应用中。鉴于其在晶体生长中的重要性[5],近几十年来围绕热毛细对流已开展了大量研究[6-7],包括理论分析、数值模拟以及地面和空间实验。Davis[8]和Schatz等[9]分别在1987年和2001年对相关内容进行了综述。
热毛细流动的稳定性直接影响晶体生长的质量,因此一直受到广泛关注。Smith等[10]采用线性稳定性方法研究了无限大平板上的热毛细液层,发现其失稳机制取决于Prandtl 数。Chan等[11]应用上述液层模型研究了重力效应对热毛细稳定性的影响,其临界参数与空间实验结果[12]相符。2016年Kang等[13]在中国 实践十号返回式科学实验卫星中对环形液池的热毛细对流进行了空间实验,结果显示流体从稳态到振荡态过程中存在定向传播的热流体波.
以往热毛细对流失稳的理论研究多采用模态分析方法,即假定小扰动随时间呈指数变化。虽然该方法可预测扰动的长时间变化,但是对于许多情况,例如管道流动,模态分析得到的临界Reynolds 数与实验观测不符。流动转捩对初始状态和外加扰动十分敏感。因此有研究发展了非模态理论,研究流动失稳的短期效应[14-17]。对于热毛细对流,在一些情况下模态分析得到的临界Reynolds数Rec量级达到Rec≈O(104)或O(105)[18],远大于一般情况下的转捩Reynolds数,因此可能存在亚临界条件下的流动失稳。此外非模态理论已应用于一些热毛细力驱动的流动,研究结果与实验相符[19]。本文采用非模态方法研究热毛细液层的流动稳定性对初始扰动和外加激励的敏感性,并 讨论Reynolds 数和Prandtl 数的影响。
1 控制方程
采用图1 所示热毛细液层模型,即厚度为d的无限长液体薄层因液面温度梯度而产生对流。x、y、z分别表示流向、展向和法向。流动为平行剪切流(包括回流和线性流)。

图1 热毛细液层模型Fig.1 Schematic of thermocapillary liquid layers
流动的无量纲控制方程组分别为连续性方程、动量方程和能量方程,即
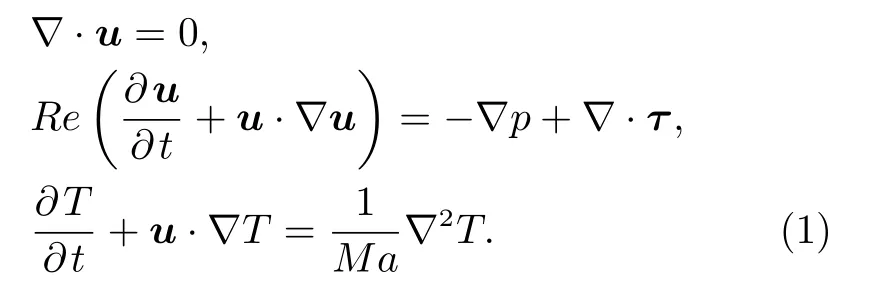
边界条件如下。
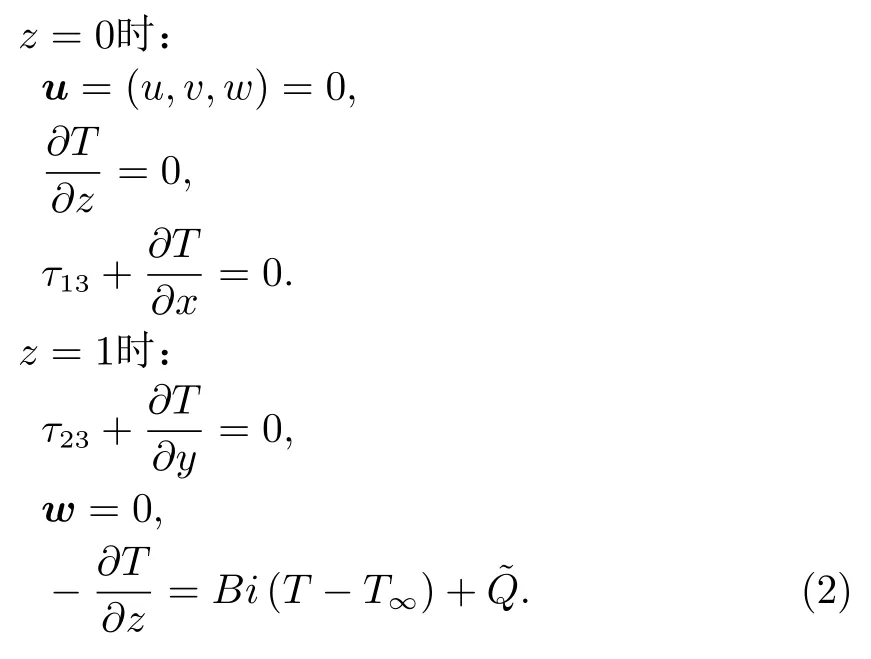
其中:u、p、T、t分别为速度、压强、温度和时间;τ为应力张量;T∞为无穷远处温度;Q˜为外加热通量。在刚性平面处(z=0),要求速度无滑移且竖直方向无热通量;在自由面处(z=1),前两式表示热毛细力提供流动剪切力,第三式表示法向速度为0,第四式表示竖直方向热通量与T −T∞呈线性关系。
Reynolds数Re、Marangoni数Ma和Prandtl数Pr分别定义为
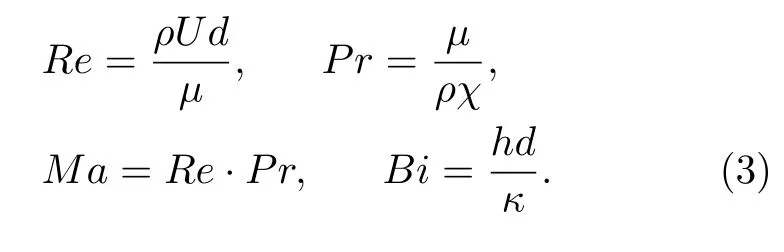
其中,ρ为流体密度,U为流体特征速度,d为液层厚度,µ为动力粘度,χ为热扩散系数,h为传热系数,κ为热导率。为了简略起见,在这里只讨论Bi=0的情况。流体为牛顿流体,则本构方程为τ=S,应变率张量S=∇u+(∇u)T。
任宏等[6]认为,该区域的矿床形成主要经历了海相热卤水喷流-沉积交代阶段、变质叠加改造阶段和近地表浅部氧化淋滤次生富集阶段三个阶段,铜钴元素的初始富集主要发生在同生沉积交代成矿阶段。热水同生沉积岩主要由海底热水发生同生沉积作用而形成,有少量陆源碎屑物质的混入。岩石发育纹层状、厚层块状等构造,硅质岩中金属硫化物呈浸染状、层纹状等产出[24]。
考虑如下两种形式的基本流[8]。线性流:
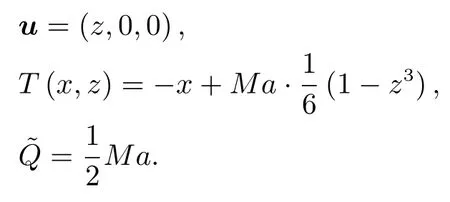
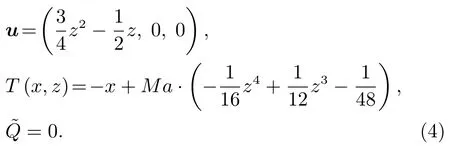
回流:前者速度呈线性分布,而后者法向质量流量为0。
以下分析流动稳定性。首先采用模态分析方法,在基本流场中叠加正则小扰动,有

其中,σ为复频率,α和β分别表示在x和y轴上的空间波数。总波数和波的方向角分别用
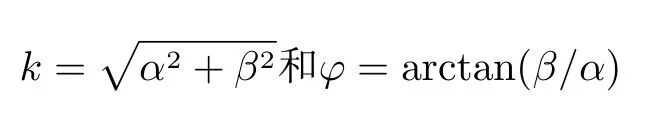
表示。σ可以通过Chebyshev 配点法求解。下标0 表示基本流,以下方程中无下标量表示扰动。
采用非模态分析方法研究初始状态和外加扰动对流动稳定性的影响。设扰动演化方程具有如下形式:
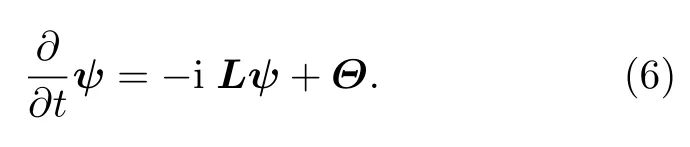
其中,ψ=(u,v,w,T)为扰动量,L为演化算子(可以由模态分析得到),Θ为外加激励。对于无外加激励的情况,可用瞬态增长函数G(t)反映流场对初始扰动的放大,即t时刻扰动能量与初始时刻扰动能量之比;对于外加激励为频率ω的简谐函数情况,可用反馈函数ℜ(ω)反映流场对外加信号的放大,即输出扰动能量与输入扰动能量之比。计算公式分别为[20]
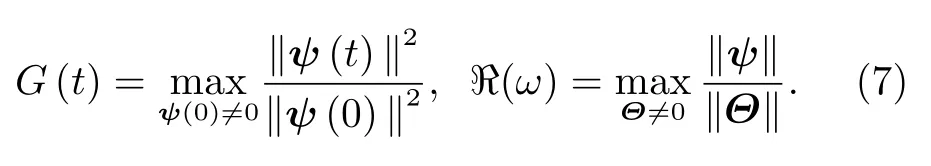
范数‖·‖2表示扰动能量E,可定义为[21]
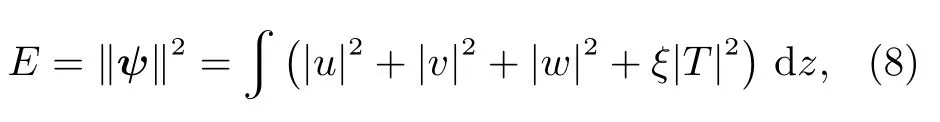
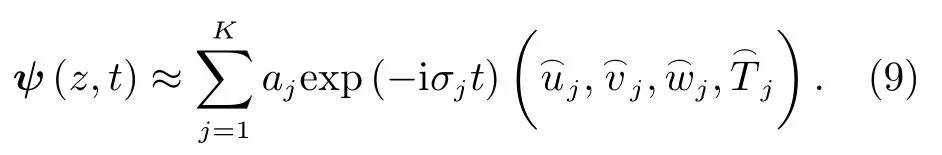
2 数值结果
图2 显示了不同Re数下扰动的瞬态增长函数G(t)。可以看到线性流小Pr下的亚临界流动中(线性流Pr=0.002 的临界Marangoni数Mac≈3.41)存在较大的瞬态增长,扰动经过一段短暂增长之后开始衰减。因此可以定义最大瞬态增长
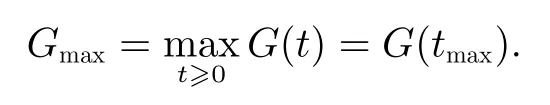
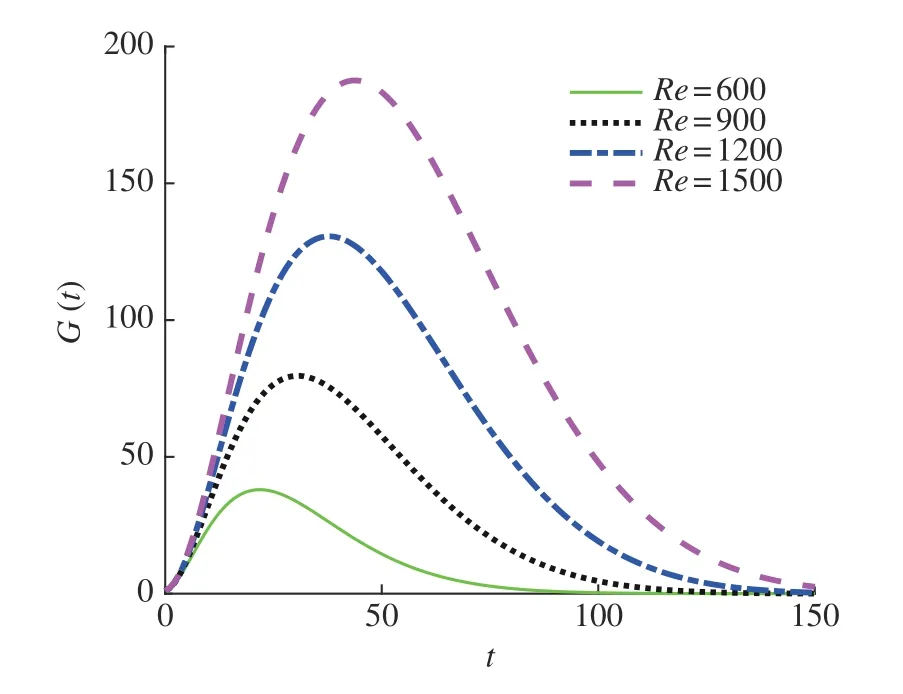
图2 线性流Pr=0.002,k=4,ϕ=90°不同Reynolds 数下瞬态增长函数G(t)随时间t 的变化Fig.2 Variation of G(t) with time of the linear flow at Pr=0.002, k=4,ϕ=90° with various Reynolds numbers
随着Re增大,Gmax及对应的时间tmax明显增大。对于反馈函数,可以类似定义最大扰动放大ℜmax=maxℜ(ω)。图3 表明在小Pr下Gmax和ℜmax近似与Re2成正比。图4 显示了大Pr下不同Pr的反馈函数ℜ(ω)。可以看到,回流大Pr下的亚临界流动中(回流Pr=150 的临界Mac≈383.7)存在较大的扰动放大。图5显示了回流大Pr下ℜmax随Pr和Re的变化,可以看到ℜmax分别随Re5和Pr5呈线性增长,渐近线分别为ℜmax≈3.28Re5+12.05和ℜmax≈1.92×10−9Pr5+15.45。能量分析表明大Pr下扰动能量主要来自表面热毛细力做功。比较瞬态增长和扰动放大的量级发现|ℜmax|2≫Gmax,表明热毛细液层对外加噪声比初始状态更为敏感。
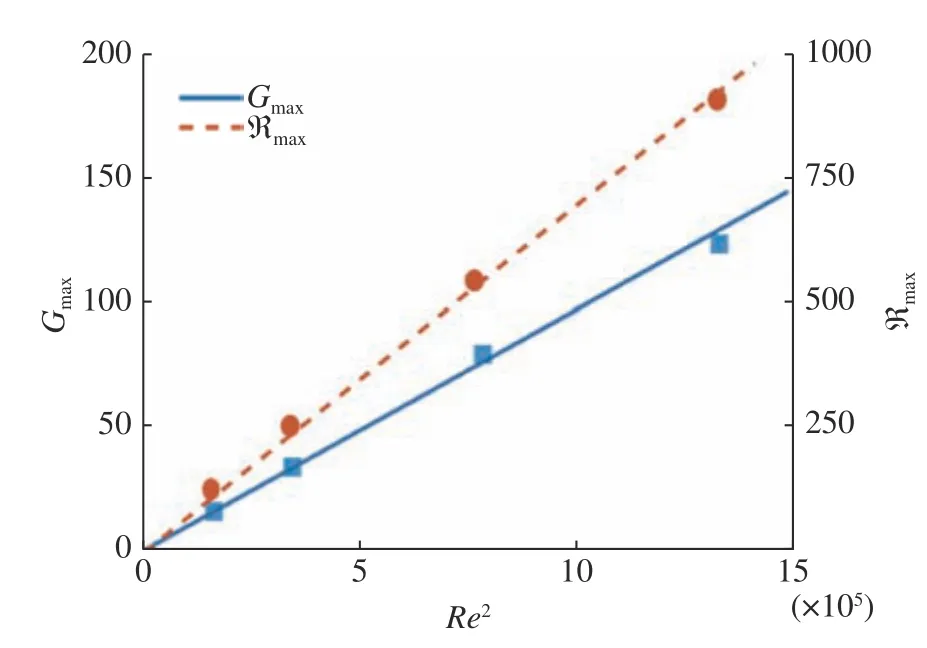
图3 线性流Pr=0.002,k=4,ϕ=90°最大瞬态增长Gmax 和最大扰动放大ℜmax随Reynolds 数的变化Fig.3 Maximum transient growth function Gmax and the maximum response function ℜmax versus Reynolds numbers of the linear flow at Pr=0.002,k=4,ϕ=90°
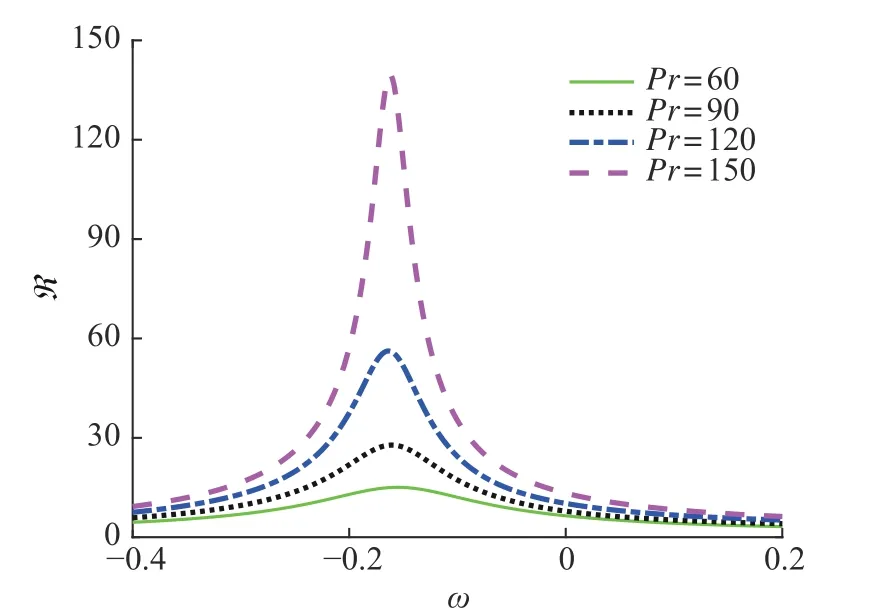
图4 回流Re=2,k=2.3,ϕ=0°不同Prandtl 数下扰动放大 ℜ随实频率 ω 的变化Fig.4 Response function ℜ versus the real frequency ω of the return flow at Re=2,k=2.3,ϕ=0°with various Prandtl numbers
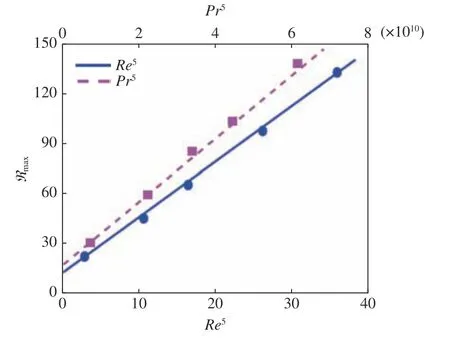
图5 回流k=2.3,ϕ=0°最大扰动放大ℜmax随Prandtl 数和Reynolds 数的变化Fig.5 Maximum response function ℜmax versus the Prandtl numbers and Reynolds numbers at k=2.3,ϕ=0°
图6 与图7 分别显示了线性流和回流对不同频率和波数外加激励的放大情况。定义最优扰动放大可以发现,相比大Pr,小Pr下的流动存在更大的扰动放大,并且小Pr数下的流动在靠近90°时取到ℜopt,而大Pr下在0°时取到该值。在平面管道流动中,ℜopt均存在于90°附近[16]。随着频率ω的增大,线性流小Pr下的最优扰动从β轴(β ≈4)变为α ≈0.45,β ≈3;大Pr回流的最优扰动从α ≈2.3减小到α ≈1.5。此结果说明随着外加激励频率ω的增大,最优扰动波数逐渐减小。

图6 线性流Pr=0.002、Ma=3 在不同实频率下α −β平面内 lgℜ的等值线Fig.6 Level lines of the logarithm of the response lgℜin the α −β plane for the linear flow at Pr=0.002,Ma=3 with various real frequency
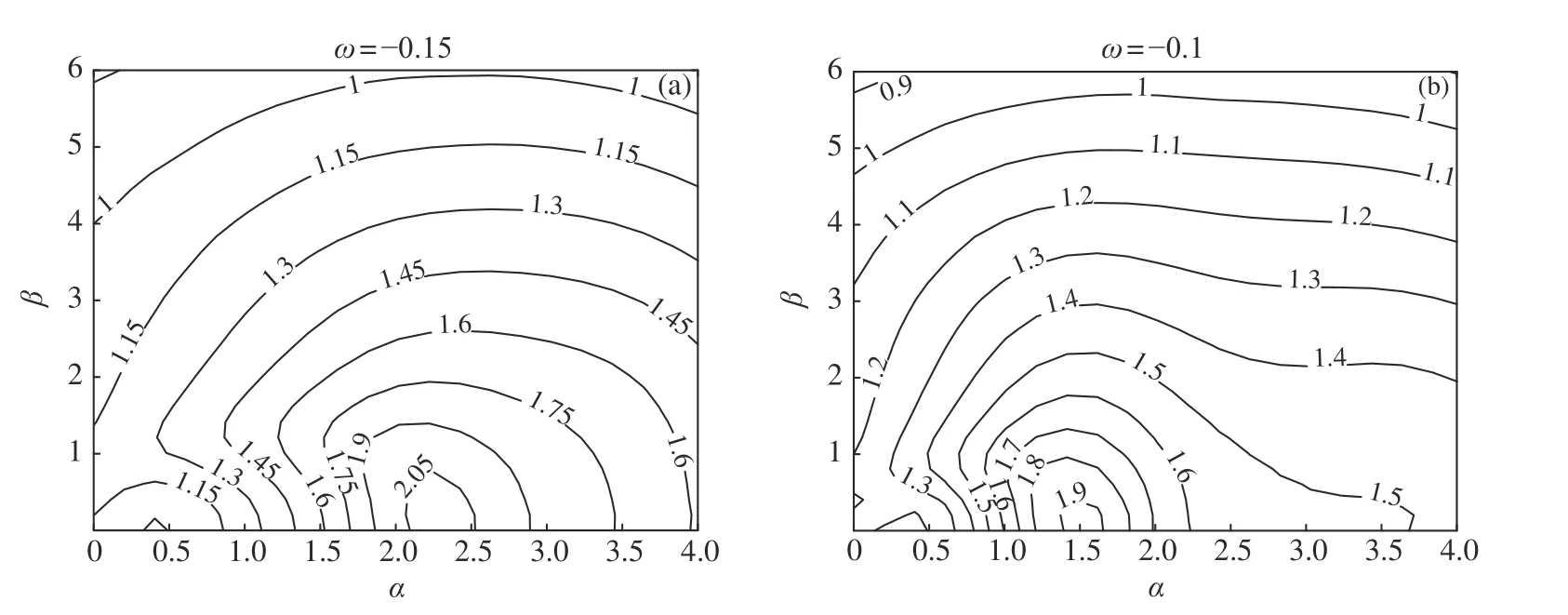
图7 回流Pr=150,Ma=300 在不同实频率下α −β平面内 lgℜ的等值线Fig.7 Level lines of the logarithm of the response lgℜin the α −β plane for the return flow at Pr=150,Ma=300 with various real frequency
图8 和图9 显示了不同Pr下输入和输出的扰动流场及温度场。可以看到扰动输出速度和温度的量级远大于输入的量级。在小Pr下输入和输出的流场中均有流向条纹(沿流速度大于或小于平均流速的狭窄区域)。此放大机制为“举起”机制[16],即流向条纹是由流向涡放大产生的。输入和输出流场在竖直方向上的涡数量分别为1 和2,而在平面管道流动中,涡数量都是1[16]。输入温度在液层底部为0,而输出温度在全场均有分布。在大Pr下,输入速度和温度只分布于靠近液面处,输出温度分布在液层内部,而在平面管道流动中,输入速度分布于全流场[16]。大Pr下Re的量级仅为O(1),此时温度场十分关键,放大主要是热毛细效应。Smith[22]发现大Pr下热毛细液层的不稳定性主要是由垂直方向热对流引起的。当Pr增大时,热对流比热传递更重要,因此ℜmax随Pr的增大而增大(见图3 和图4)。
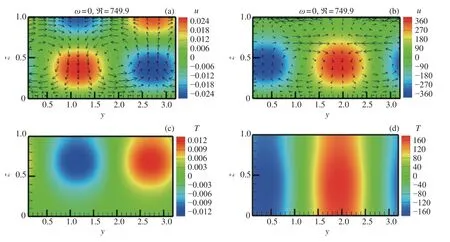
图8 线性流Pr=0.002,Ma=3,k=2,ϕ=90° 扰动放大对应的扰动场。(a) 输入速度场,(b) 输出速度场,(c) 输入温度场,(d) 输出温度场Fig.8 Perturbation fields corresponding to the response for the linear flow at Pr=0.002, Ma=3, k=2,ϕ=90°.(a) Input velocity field,(b) output velocity field,(c) input temperature field and(d) output temperature field
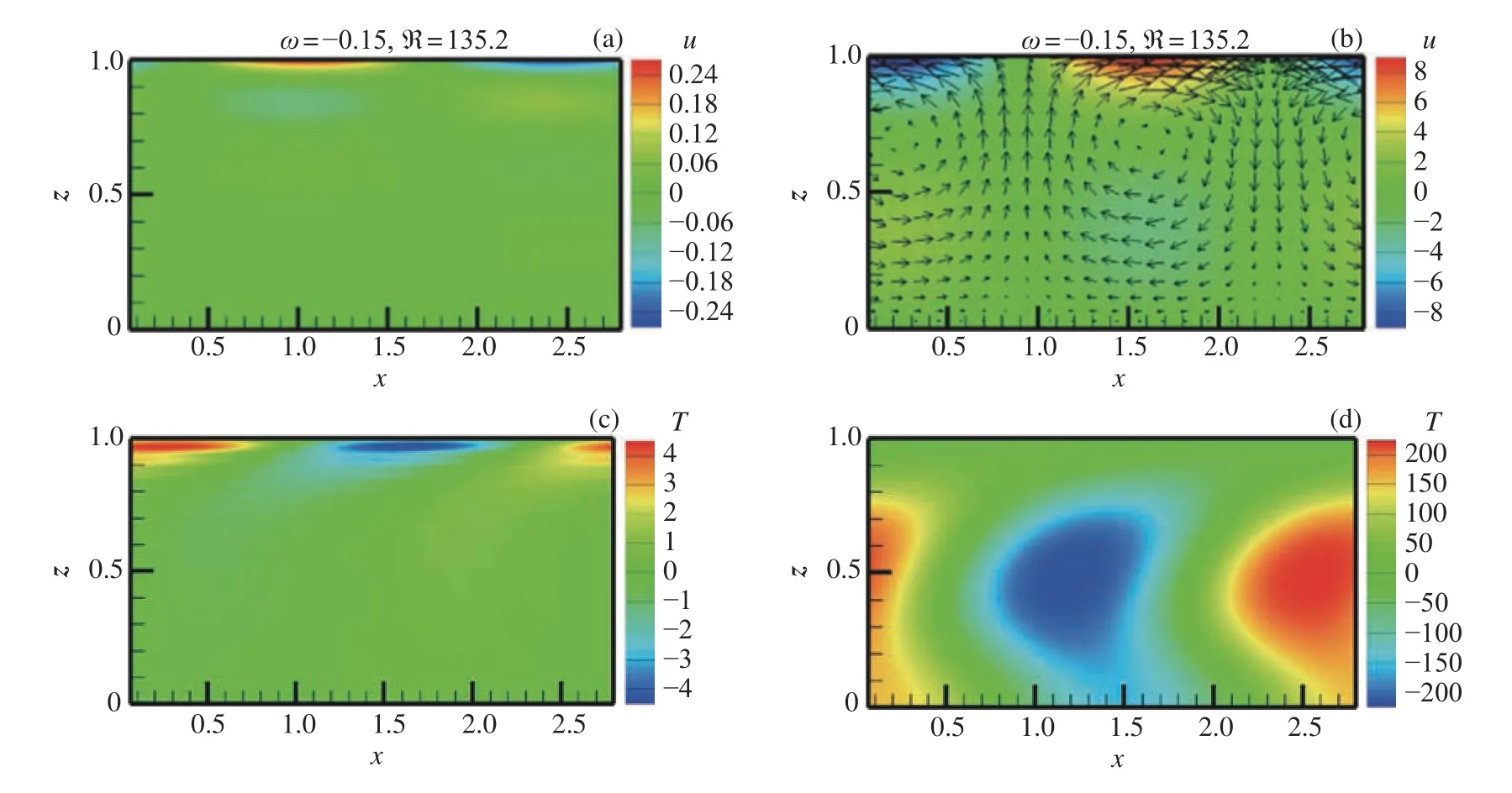
图9 回流Pr=150,Ma=300,k=2.3,ϕ=0° 扰动放大对应的扰动场。(a) 输入速度场,(b) 输出速度场,(c) 输入温度场,(d) 输出温度场Fig.9 Perturbation fields corresponding to the response for the return flow at Pr=150, Ma=300,k=2.3,ϕ=0°.(a) Input velocity field,(b) output velocity field,(c) input temperature field and(d) output temperature field
3 结论
利用非模态稳定性方法研究了热毛细液层对初始扰动和外加激励的放大,得到以下结论。
(1)线性流和回流小Pr下的亚临界流动对初始扰动和外加激励均十分敏感,最大瞬态增长Gmax和最大扰动放大ℜmax与Re2近似成正比。
(2)回流大Pr下的亚临界流动中存在对外加激励的显著放大,ℜmax分别随Re5和Pr5呈线性增长。
(3)相比于大Pr,小Pr的流动存在更大的扰动放大。随着外加激励频率ω的增大,最优扰动波数逐渐减小。
(4)流场和温度场表明,扰动输出速度和温度的量级远大于输入的量级。在小Pr下,输入和输出的流场中均有流向条纹,但竖直方向的涡数量及温度分布不同;在大Pr下输入的速度和温度只分布于靠近液面处,而输出温度分布在液层内部。两者放大机制不同。
