基于施工过程的大断面隧道变形动态释放规律分析*

孙州

(1.上海同岩土木工程科技股份有限公司， 上海 200092；2.上海同岩公路养护工程有限公司， 上海 200092；3.上海地下基础设施安全检测与养护装备工程技术研究中心， 上海 200092)

随着高速公路的快速发展，大断面隧道数量增多。国内外学者针对大断面隧道开展了大量研究，如刘长祥等分析了大断面隧道围岩的变形过程；何昌国分析了大跨隧道合理预留变形量；单超等分析了大跨浅埋隧道偏压段的横向偏移规律；曹成勇等结合下穿高速公路大跨隧道，分析了隧道开挖的力学行为；李利平等分析了大断面隧道围岩的渐进破坏过程；吕志强结合东天山隧道，研究了大断面隧道的开挖支护技术；郭军等对大跨公路隧道进行了支护参数优化分析；伍国军等结合施工过程，对浅埋大跨公路隧道进行了支护参数优化分析；蔡鑫等分析了附加荷载作用下大跨隧道的围岩压力和结构内力变化规律；王仁杰等进行了大跨隧道扁平率优化研究。上述研究多侧重于大断面隧道支护参数的优化。该文依托宁波将军山隧道，开展大断面隧道变形动态释放规律研究，探索合理的支护施作时机，为类似工程提供参考。

1 工程概况

将军山隧道沿线地形为中间高、两端低，沟谷纵横，风化强烈，山上植被茂盛，覆盖层为第四系残积土和坡洪积碎石、含砾石粉质黏土，下伏为全～微风化晚侏罗统西山头组凝灰岩。隧道净空断面宽度为16.8 m，高度为10.85 m，高跨比为0.65，属于大断面隧道。

根据围岩级别和隧道断面情况，隧道Ⅴ级围岩段采用复合式衬砌结构形式：初期支护为φ42×5双排小导管，长5 m，纵向间距3 m，环向间距0.42 m；中空注浆锚杆长4.5 m，纵向间距0.5 m，环向间距1.0 m；喷射砼，第一层厚度为26 cm，采用I20b型钢@0.50 m，第二层厚度为20 cm，采用φ25格栅拱架@0.50 m；二次衬砌采用C40砼，厚度55 cm。

2 计算模型与参数选取

2.1 建立模型

基于现场Ⅴ级围岩段地质特征建立三维数值计算模型，超前小导管注浆加固采用实体单元模拟，锚杆采用Cable结构单元模拟，初期支护采用Shell结构单元模拟。隧道埋深约18 m，模型长、宽、高分别为180、100、55 m。左右边界为水平约束，下边界为垂直约束，上边界为自由边界。沿隧道纵向50～90 m处分别在拱顶、边墙每隔20 m设置监测点。计算模型见图1。

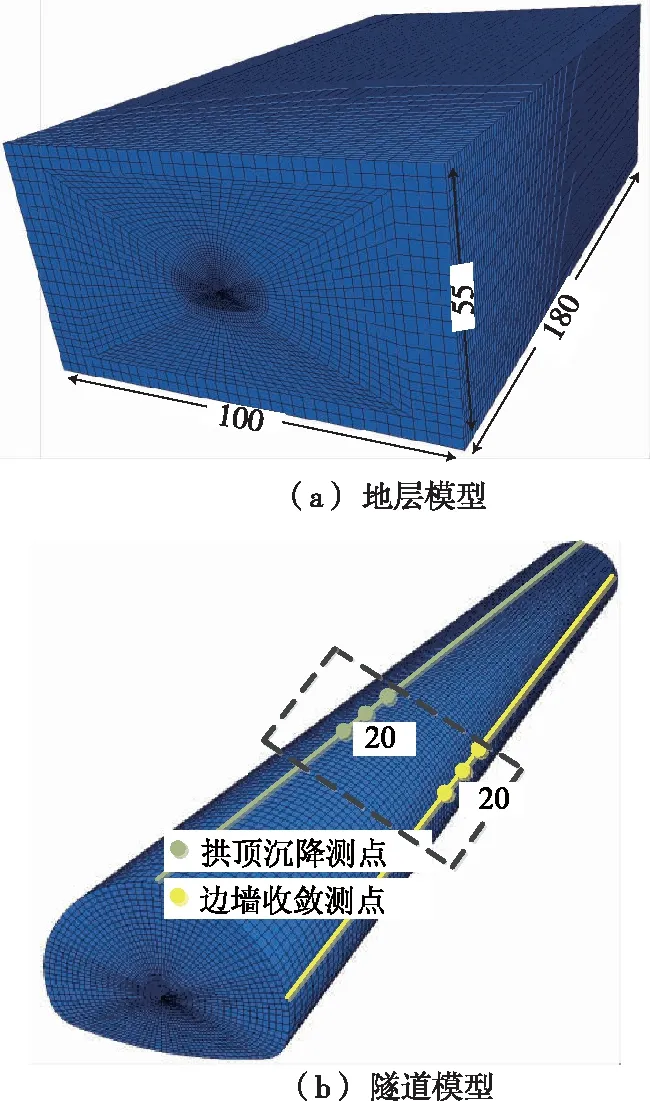
图1 隧道计算模型(单位：m)

2.2 参数选取

根据JTG 3370.1—2018《公路隧道设计规范》，各级围岩的力学参数见表1。

表1 围岩的物理力学参数

初期支护结构弹性模量根据钢筋砼计算原理采用等效截面计算，即将钢拱架、格栅拱架弹性模量折算为喷射砼弹性模量。计算方法为：

E=E0+AgEg/Ac

式中：E为折算后砼弹性模量；E0为原砼弹性模量；Ag为钢拱架截面积；Eg为钢材弹性模量；Ac为喷射砼截面积。

锚杆与围岩之间采用摩擦接触，围岩与初期支护及初期支护与二次衬砌之间采用共节点模拟。锚杆等的力学参数见表2、表3。

表2 锚杆的力学参数

表3 钢拱架等的力学参数

2.3 模拟工序

采用台阶法开挖，上台阶长度为15 m、开挖进尺为1 m，下台阶开挖进尺为3 m。台阶法计算模型见图2。

图2 台阶法计算模型

3 隧道变形动态释放规律分析

3.1 拱顶沉降

不同监测点的隧道拱顶沉降随开挖进尺的变化见图3。由图3可知：拱顶3个测点的沉降随开挖进尺的释放规律基本一致，均随着开挖进尺的增加而逐渐增大，分为缓慢增长、快速增长、趋于稳定3个阶段，距施工掌子面距离越近的测点，其沉降开始时间、稳定时间越早。隧道未开挖到监测断面时，拱顶沉降为4 mm；隧道监测断面上台阶开挖前，拱顶沉降释放20%；下台阶开挖前，拱顶沉降为9.6 mm，释放48%。根据《公路隧道施工技术规范》，二次衬砌施作应在变形基本稳定(位移达到总位移的80%～100%)后进行，二次衬砌施作时机建议距离开挖面42～60 m。

图3 拱顶沉降随开挖进尺的变化

拱顶沉降速度随开挖进尺的变化表现为先增加后减小(见图4)。以1号监测断面为例，开挖距离该监测断面越近，该断面的沉降速率越大，开挖到该断面时，沉降速率达到最大，为0.6 mm/m；之后随着开挖距离的增大，沉降速度逐渐减小，最终趋于稳定，沉降值约20 mm。

图4 拱顶沉降速度随开挖进尺的变化

3.2 边墙收敛

不同监测点的隧道边墙收敛随开挖进尺的变化见图5。由图5可知：3个测点左右边墙收敛随开挖进尺的变化规律一致，随施工推进，边墙收敛逐渐增大，收敛速度呈先增大后减小的趋势。以1号监测点为例，开挖到达该监测断面前，沉降速度逐渐增大，到达开挖断面时，变形速率达到最大，为0.55 mm/m，收敛变形为1.25 mm。监测断面上台阶开挖前，边墙收敛释放15.6%；下台阶开挖前，收敛变形为5.2 mm，边墙收敛释放65%；之后随着开挖距离的增大，沉降速度逐渐减小，最后趋于零，隧道收敛变形为8 mm。

图5 边墙收敛随开挖进尺的变化

3.3 锚杆轴力

隧道锚杆轴力分布见图6。各部位锚杆轴力均为拉力，整体表现为边墙和拱腰处锚杆轴力值大、拱顶和拱脚处锚杆轴力值小，断面内锚杆轴力最大值位于左右边墙位置，约45 kN。

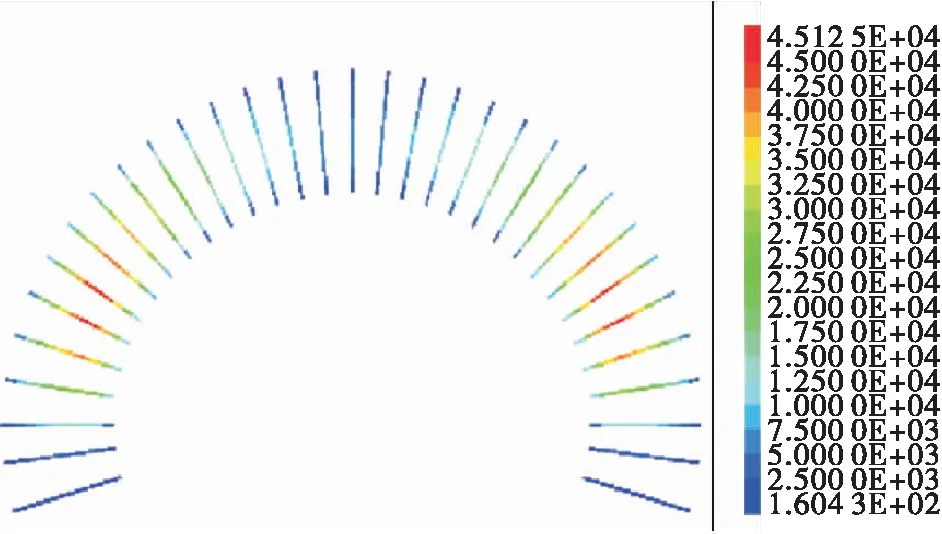
图6 中间断面锚杆轴力分布(单位：N)

选取监测断面内轴力最大的锚杆为监测锚杆，得到锚杆轴力随开挖进尺的变化曲线(见图7)。锚杆轴力的变化规律与拱顶沉降、边墙收敛基本一致，随着开挖进尺的增大而增大，但增大速度逐渐减小，最终趋于稳定，锚杆轴力稳定值约45 kN。锚杆有效控制了隧道周围岩体的变形，起到了悬吊加固与抑制围岩变形的作用。

图7 锚杆轴力随开挖进尺的变化

4 现场监测与分析

4.1 围岩压力分析

围岩压力的变化见图8。由图8可知：上台阶开挖后，围岩压力快速增加，随着围岩应力的重新分布，压力有所降低，拱顶与右拱腰处压力释放较大，分别为43.6%、49.2%；下台阶开挖后，围岩压力继续增加；二次衬砌施作后，各部位围岩压力逐渐趋于稳定。拱顶和右边墙处围岩压力较大，最大压力为150.2 kPa；左、右拱腰处的压力较小，分别为84.1、92.9 kPa。隧道围岩压力分布整体呈对称形式(见图9)。

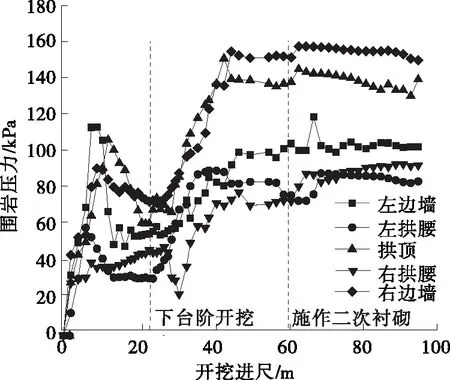
图8 围岩压力随开挖进尺的变化

图9 围岩压力分布(单位：kPa)

4.2 锚杆轴力分析

锚杆轴力随隧道开挖进尺的变化见图10。由图10可知：上台阶开挖后，锚杆轴力迅速增加，各部位锚杆处于受拉状态，拱顶处锚杆轴力最大；下台阶开挖后，锚杆轴力变化不大，最大为33.1 kN(68.6 MPa)，相对于模拟值偏小，主要是因为隧道开挖到锚杆支护位置时围岩已释放一部分变形，锚杆施作相对滞后。锚杆轴力分布整体表现为锚杆中心轴力大、两端轴力小(见图11)，表明锚杆穿过了围岩松动区，起到了悬吊加固与抑制围岩变形的作用。

图10 锚杆轴力随开挖进尺的变化

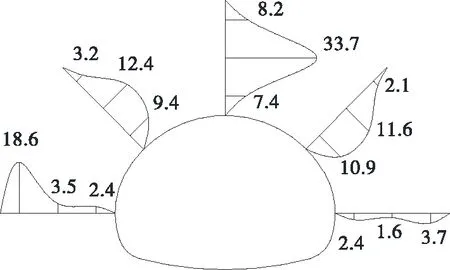
图11 锚杆轴力分布(单位：kN)

4.3 围岩变形

拱顶沉降随开挖进尺的变化见图12。隧道上台阶开挖后，拱顶沉降逐渐增加，前期沉降速度较快，之后沉降速率逐渐减小，最后拱顶沉降稳定为6.5 mm。拱顶和拱顶左边部分下沉量相对右边较大，且略有波动，主要是由于距离掌子面较近，受到前方爆破震动的影响。下台阶开挖后，拱顶沉降增加2 mm，总体沉降约8 mm，相对于数值模拟结果偏小，原因是隧道开挖前围岩已释放一部分变形、施作二次衬砌后没有继续监测围岩变形。

图12 拱顶沉降随开挖进尺的变化

隧道净空收敛的变化见图13。隧道整体向内收敛，最大值为6.5 mm，相对于模拟值偏小19%，主要是因为隧道开挖前围岩已释放一部分变形。

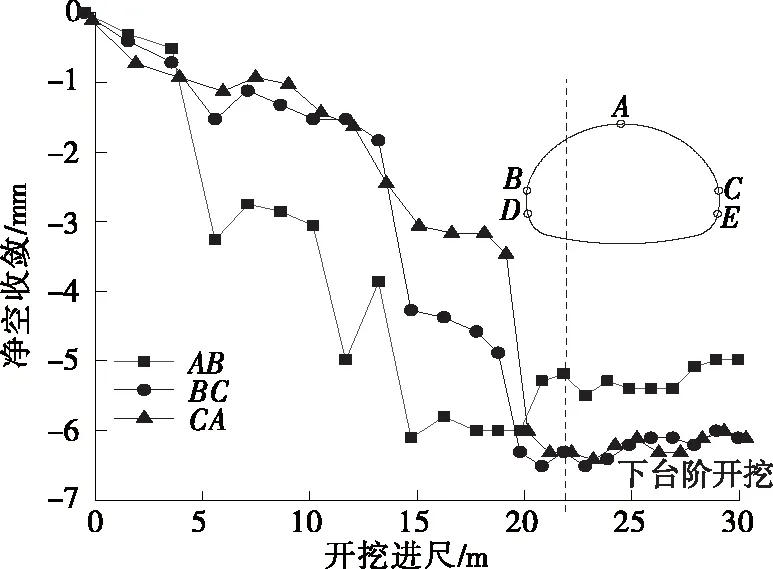
图13 净空收敛随开挖进尺的变化

5 结论

(1) 沿隧道纵向，隧道变形随开挖进尺的释放规律基本一致，变形随着开挖进尺的增加而增大，分为缓慢增长、快速增加、趋于稳定3个阶段。上台阶开挖后变形释放48%～65%，围岩压力释放43.6%～49.2%。

(2) 隧道变形收敛、锚杆轴力实测值分别比模拟值减小19%、27%，主要是由于隧道开挖前围岩已释放一部分变形。监测数据表明各指标均处于稳定状态。

(3) 隧道二次衬砌施作时机建议距离开挖面42～60 m。采用台阶法施工时，严格控制循环进尺、台阶长度等参数，从而确保围岩的稳定。