成兰铁路软岩隧道大变形控制技术及变形控制基准研究
2022-04-13郭小龙谭忠盛
郭小龙,谭忠盛,喻 渝
(1.北京交通大学 土木建筑工程学院, 北京 100044;2.中铁二院工程集团有限责任公司,四川 成都 610031)
高地应力软岩条件下挤压型大变形控制是目前隧道及地下工程领域面临的重要难题,国内外学者对此开展大量研究和实践,取得了丰硕的研究成果[1]。在支护理论方面,形成了轴变理论[2]、联合支护理论[3]、弧板支护理论[4]、松动圈理论[5]、主次承载区支护理论[6]、关键部位耦合支护理念[7]等。从支护理念上可分为刚性支护和柔性支护两大类,刚性支护包括高强弧板、提前施作大刚度二衬、重型拱架、钢管混凝土拱架等,柔性支护包括让压锚杆[8]、可缩性拱架[9-10]等。
随着大变形隧道实践工程的不断推动,发现单一的控制措施往往难以奏效,为此出现众多大变形联合控制措施,包括开挖方法、地应力调整、支护体系、变形控制标准等,进而形成复杂的变形控制技术。如乌鞘岭隧道采用断面形状优化、加大预留变形量、多重支护及加大衬砌刚度的支护结构,同时开挖方法上采用以实现快速封闭的短台阶及超短台阶法[11-12];兰渝铁路出现大量挤压型大变形隧道,包括木寨岭隧道[13]、两水隧道[14]、毛羽山隧道[15]等,其中尤其以木寨岭隧道变形最为严重,提出导洞应力释放,多层圆形支护,长锚杆(索),注浆加固的综合变形控制方案,同时提出了大变形控制分级管理理论和施工控制标准。随着大变形隧道围岩挤压程度不断提高,变形控制技术研究也逐渐从单一工况向考虑不同挤压程度的变形控制体系进行完善[16-17]。
从上述分析可以看出,虽然目前针对软岩隧道大变形控制技术已经从单一控制措施向多种措施联合应用发展,同时向不同大变形等级的变形控制体系逐渐完善。但目前来看大变形控制理念不明确,缺乏针对不同大变形等级,适用性强的软岩隧道大变形控制体系。
隧道变形控制基准是实现隧道信息化施工的重要基础,又是提高隧道施工安全性、经济性的重要手段[18]。尤其软岩隧道变形量大,变形速率快,如果预留变形量不足,即使围岩变形得到控制,依然会导致拆除支护、进行扩挖的后果[19]。随着新奥法的推广应用,国内外学者对隧道变形规律及控制基准进行了广泛研究。文献[20]认为通过大刚度支护控制深埋软岩隧道变形不仅不科学而且经济性差,应有一定的变形释放,其预留变形量约为20~30 cm。赵东平等[21]通过现场量测数据分析,基于一定保证率,建立了大断面黄土隧道预留变形量。王明年等[18]基于变形数据分析,提出了大断面海底隧道CRD法绝对位移控制基准。我国的铁路隧道设计规范中考虑隧道跨度、埋深、开挖方法等因素,对常规围岩分级条件下隧道预留变形量及变形控制基准进行了详细规定,但对于软岩隧道如何通过监控量测数据反馈分析得到变形控制基准未给出明确解答。因此许多学者采用理论分析[22]、数值计算[23-24]、模型试验[25-26]及现场试验[27-28]等方法对软岩隧道预留变形量及变形控制基准进行了研究。上述关于软岩隧道变形控制基准的研究中,大多以隧道预留变形量作为主要研究对象,未考虑基于施工过程的隧道变形特征建立变形控制基准。同时考虑大变形分级,针对不同变形控制体系,系统性建立软岩隧道变形控制基准的研究较少。
本文以成(都)兰(州)铁路典型软岩隧道工程为依托,基于大量工程实践,提出成兰铁路软岩隧道大变形控制理念及变形控制体系。同时对大量变形量测数据进行统计分析,考虑施工过程中变形发展规律,建立软岩隧道变形控制基准。
1 工程概况
成兰铁路为国铁Ⅰ级双线电气化铁路,采用客货共运,设计时速200 km/h,线路最小曲线半径为3 500 m,最大坡度9‰。
线路起于成都,向北经松潘、九寨沟接入兰渝铁路的哈达铺站。线路总长457 km,隧道总长332 km,占路线总长度的73%,其中53%的隧道段落穿越软岩地层。路线位于印度板块与欧亚板块相互碰撞缝合带附近,地质构造复杂,构造运动强烈,穿越龙门山断裂带,西秦岭断裂带和岷山断裂带,路线走向与主要构造带位置关系见图1。软岩地层主要为千枚岩、板岩,岩体强度低,整体性差,在高构造应力作用下挤压明显,极易造成隧道大变形[29-30]。
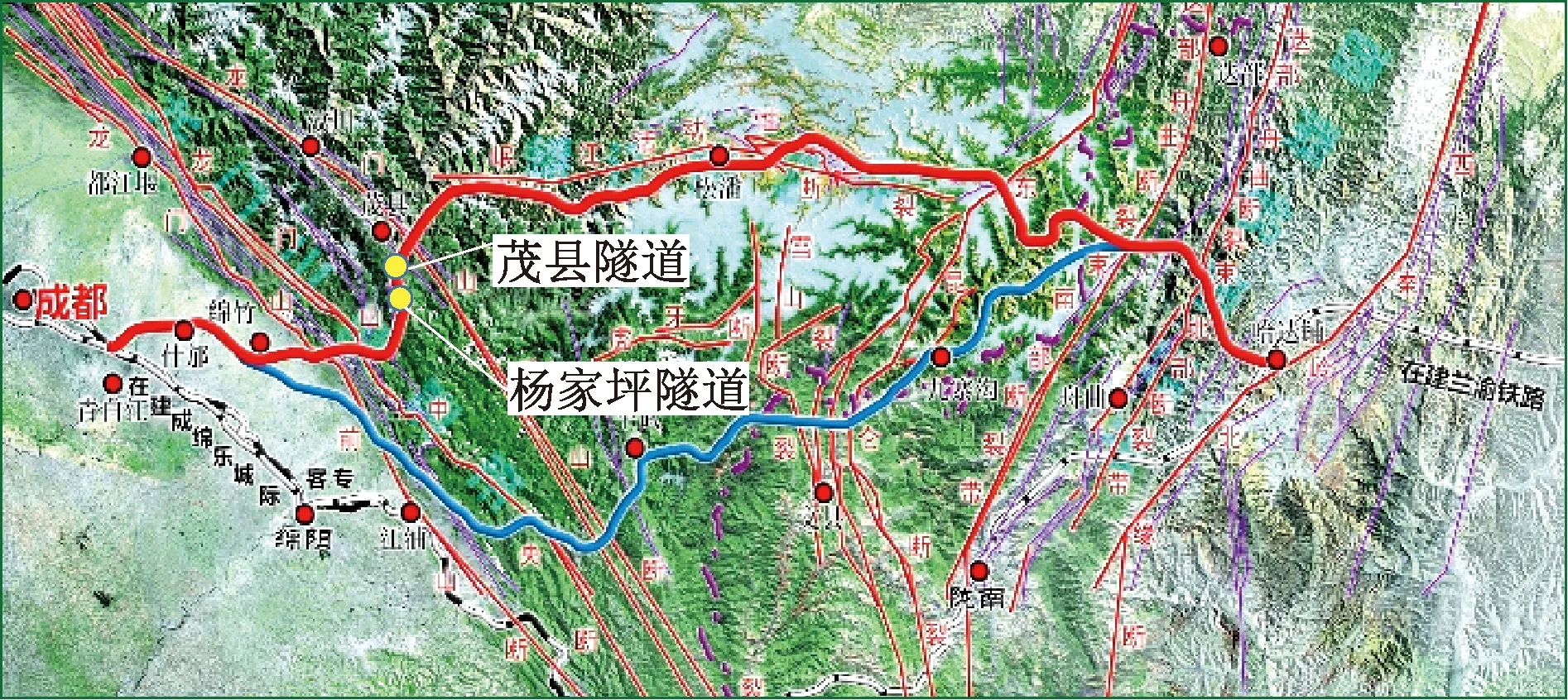
图1 成兰铁路走向及主要地质构造
本文以发生典型大变形的杨家坪隧道和茂县隧道为研究对象。杨家坪隧道全长12.84 km,最大埋深约718 m。茂县隧道全长10.01 km,最大埋深约1 656 m,两隧道通过核桃沟双线大桥相连。两隧道软岩段围岩主要为志留系茂县群千枚岩,受龙门山后山断裂带影响,岩体破碎,岩石单轴抗压强度为0.46~2.86 MPa[31-33],隧道开挖后岩石粉化现象严重。
2 大变形控制理念及大变形分级
2.1 大变形控制理念
目前国内外软岩大变形隧道工程实践中存在多种变形控制理念,包括“以抗为主”“抗放结合”“主动控制”等。
“以抗为主”是指通过大刚度初期支护(单层或多层)控制围岩变形,当围岩变形持续发展时提前施作大刚度二次衬砌以抵抗围岩变形。上述思路在实践过程中均有成功及失败案例。通过调研分析认为,“以抗为主”的理论成功控制围岩变形的案例多以轻微大变形等级为主,在实施过程中甚至体现出施工成本相对较低,施工效率高的优点。但随着围岩挤压程度不断提高,大变形等级不断增大,不少工程出现了二次衬砌开裂问题。因此,随着大变形等级增大,目前的控制体系不能承受极高的应力荷载,“以抗为主”的大变形控制理论难以取得成功[34-35]。“抗放结合”是指针对软岩隧道施工过程中对围岩变形进行适度释放,但围岩变形的释放需通过支护结构进行有效约束[19]。
随着对软岩隧道变形因素及变形机制认识的不断加深,逐渐认识到常规的被动提供支护功能的支护体系无法有效提高围岩的稳定性,不能达到“围岩支护围岩”的效果。因此,对于软岩隧道应采用“主动控制”理念,以改善围岩的应力状态为核心,减少对围岩扰动的同时主动加固围岩,充分发挥围岩的自承能力。
2.2 大变形分级标准
对隧道大变形进行分级,进而采用针对性措施,既可有效控制大变形,又可以节约成本[36-37]。Hoek等[38]提出了无支护条件下强度应力比与相对变形量的关系曲线,建立了被广泛采用的大变形分级标准。此外众多学者对大变形分级方法及标准进行了研究,分级指标多采用强度应力比和相对变形量,还包括初始地应力、绝对位移、弹性模量及综合系数等[39-41]。成兰铁路隧道工程基于大量实测数据,考虑一定支护抗力,形成大变形分级标准[42],见表1。

表1 成兰铁路隧道大变形分级标准
3 成兰铁路软岩隧道大变形控制技术
基于上述“主动控制”理念,成兰铁路提出“优化断面,强化锚杆、减少开挖分步,动态调整,分级控制”的软岩隧道大变形控制技术。
基于大变形分级,逐步优化隧道断面,提高支护结构的整体受力性能,又避免开挖空间的过度浪费。针对软岩隧道变形速率快的特点,选择合理的锚杆类型与参数,提高施工效率,及时发挥作用控制围岩变形。同时尽量减少开挖分步,轻微大变形段采用二台阶带仰拱法,中等大变形段采用二台阶法,严重与极严重大变形段采用三台阶法,施工过程严格控制台阶长度,初期支护尽早封闭成环,从而及时为围岩提供支护抗力。通过加深地质工作,探明隧址区的地应力及岩体强度特征,结合已开挖段变形特征,采用动态设计的手段,及时调整大变形等级,采取相应措施[43]。
结合成兰铁路软岩隧道大变形控制实践,对上述变形控制措施进一步说明。
3.1 断面优化
施工期间针对成兰铁路典型软岩隧道进行了地应力测试,包括茂县隧道、杨家坪隧道、柿子园隧道、松潘隧道、榴桐寨隧道等。测试结果表明成兰铁路隧址区地应力场类型为σH>σh>σv型,以水平应力为主。如杨家坪隧道最大水平主应力(σH)平均值为21.86 MPa,最小水平主应力(σh)平均值为11.51 MPa,垂直应力(σv)为8.81~9.98 MPa,水平侧压力系数达2.19~2.48。茂县隧道最大水平主应力为25.99 MPa,最小水平主应力为20.00 MPa,水平侧压力系数为1.58[44-46]。成兰铁路隧址区以构造应力为主,边墙位置受构造应力的强烈挤压作用,边墙变形显著,支护结构极易造成弯曲变形破坏。单线铁路隧道“瘦高型”断面形式对边墙变形及应力控制不利,同时仰拱较大矢跨比也不利于结构受力。虽然圆形断面整体受力效果更好,但空间利用率低,施工成本高[37]。因此,基于大变形分级,考虑结构受力和施工成本,逐渐增大隧道边墙曲率,增大仰拱矢跨比,从而改善结构受力,控制隧道变形,见图2、图3。图中S、L分别为仰拱的计算关系矢高、计算跨度。

图2 单线隧道支护结构断面示意(单位:cm)

图3 双线隧道支护结构断面示意(单位:cm)
3.2 锚杆支护技术
锚杆作为主动控制技术的重要组成部分,在控制软岩隧道大变形方面具有重要作用[36]。为充分发挥锚杆的主动控制作用,成兰铁路在软岩隧道锚杆形式、支护参数、施工机械、作用效果等方面进行了研究。
3.2.1 锚杆类型分析
目前锚杆形式众多,受力原理及作用效果存在显著差别。端锚式锚杆虽然施作简单,技术成熟,但由于软岩隧道围岩强度低,难以产生足够的锚固力。软岩隧道由于围岩松软、强度低、有明显的塑性变形,围岩可能产生沿锚杆的流动变形,因此,这类岩体应采用全长黏结式锚杆[19]。
此外,由于软岩隧道锚杆成孔困难,钻孔深度大,导致灌浆效率低,施工质量差,因此传统的砂浆锚杆适应性较差。自进式中空锚杆钻、锚一次成型,同时通过中空杆体进行压力注浆,不仅可以提高锚杆的施工效率,而且保证施工质量。因此成兰铁路软岩大变形隧道优先选用自进式中空锚杆。
3.2.2 锚杆支护参数
一般认为锚杆长度主要取决于围岩松动圈厚度,锚杆应穿透松动圈。因此为了充分发挥锚杆主动控制围岩变形的作用,结合围岩松动圈测试结果,对锚杆参数进行优化[34]。
采用声波法和地质雷达法开展了围岩松动圈值测试,测点布置见图4。严重大变形段围岩波速随深度变化规律见图5,1#测点由于难以进行保水耦合,未测得围岩波速。取边墙围岩松动圈平均值,最终围岩松动圈测试结果见表2[42]。
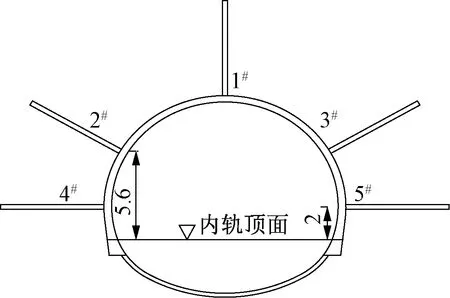
图4 声波法测点布置示意(单位:m)

图5 严重大变形段围岩波速随深刻变化规律

表2 围岩松动圈测试结果
结合不同等级大变形隧道围岩松动圈范围,锚杆长度见表3[42]。
基于围岩松动圈测试结果,建立围岩强度应力比与松动圈厚度的拟合式为
LP=-3.244lnNc-0.315
(1)
式中:LP为围岩松动圈厚度,m;Nc为岩体强度应变比。

表3 软岩大变形隧道松动圈值及锚杆长度
全长黏结锚杆承载力计算式[47]为
(2)
式中:Sa、Sb为锚杆纵向、环向间距;ψ为锚固长度对黏结强度的影响系数;Pa,b为锚杆支护抗力;D为锚杆钻孔直径,取50 mm;L为锚杆锚固长度,取锚杆长度的一半;fmg为黏结材料与围岩黏结强度,软岩地层取0.3~0.8。
假定锚杆提供的支护力与初始地应力之比为0.04,考虑锚杆纵向间距与钢拱架的关系,参考相关工程经验,纵向间距取1.2 m,则锚杆环向间距计算结果见表4。
则软岩隧道锚杆支护参数见表5。

表5 锚杆参数优化
对于严重及极严重大变形段,采用长短组合锚杆进行支护。长短锚杆对大变形控制作用分别从力学机制和施工工艺两方面进行分析。首先隧道开挖后围岩为渐进式破坏,松动圈随开挖和时间逐渐增大,施作短而密的锚杆,可有效提高围岩力学性质,形成承载拱,发挥围岩的承载能力。随着松动圈的进一步发展,短锚杆随塑性区整体向内移动,长锚杆施作后将承载拱与深部围岩形成整体,使围岩应力向深部转移,从而有效降低结构荷载。其次,由于隧道围岩稳定性极差,多采用三台阶法(预留核心土)进行施工,施工空间严重制约了长锚杆的施作,使锚杆施作时机滞后,上台阶锚杆在中台阶开挖后进行施作,不能及时发挥锚杆锚固作用。长短组合锚杆指隧道拱部先进行短锚杆施作,待中台阶开挖完成后一次性完成中上台阶长锚杆施作。短锚杆可以及时施作,对浅层围岩进行及时加固,与拱架共同作用,提供的支护反力可以减少即时松动圈内剪胀变形,同时使浅层围岩形成压缩拱,改善结构受力,控制围岩变形[48-50]。
短锚杆应达到围岩瞬时松动圈厚度,长锚杆达到稳定松动圈厚度,其中瞬时松动圈按60%稳定松动圈厚度确定[5]。
3.2.3 长短组合支护效果
为进一步明确长短组合锚杆在软岩隧道中的变形控制作用,在茂县隧道1#斜井(严重大变形段)开展了等长锚杆、长短组合锚杆对比试验,其中长短组合锚杆布置示意见图6[46,51]。XJ1K0+232~220为等长的8 m锚杆试验段,记为A1试验段;XJ1K0+220~208为长短组合锚杆试验段,长锚杆为8 m,短锚杆为3 m,记为A2试验段。试验段长锚杆轴力分布见图7。

图6 长短组合锚杆布置示意
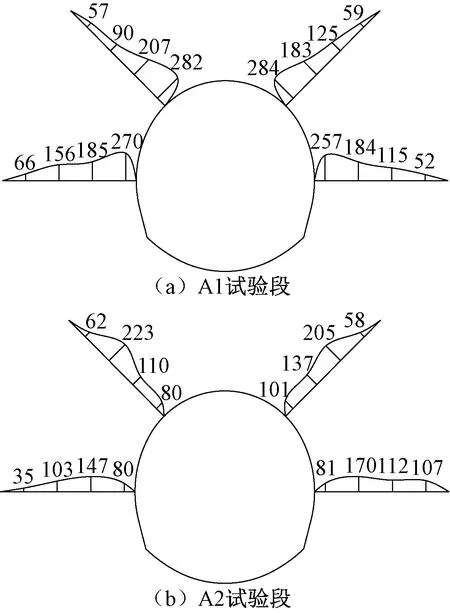
图7 锚杆对比试验段锚杆受力包络图(单位:kN)
由图7可知,等长锚杆与长短组合锚杆试验段长锚杆轴力分布明显不同,等长锚杆轴力随着围岩深度增加逐渐减小,而长短组合锚杆轴力呈现中间大,两头小的分布。其主要原因是软岩大变形隧道中浅层围岩破坏非常严重,变形量大,使锚杆轴力非常大,同时,台阶施工时在拱架下沉作用下,一定的剪应力使轴力增长。而长短组合锚杆由于短锚杆形成的浅层压缩拱使浅层围岩变形相对较小,降低了长锚杆浅层段剪应力,长锚杆为使浅层压缩拱与深层围岩协调变形,中性点向深部围岩转移。
两组试验典型断面隧道变形时程曲线见图8。图8中,A为拱顶下沉,S1、S2为边墙收敛。

图8 试验段变形时程曲线
由图8可知,从变形发展过程来看,上台阶施工完成后两试验段变形量基本相当,但由于A2试验段采用了长短组合锚杆支护,隧道变形速率及最终变形量明显小于A1试验段,可使拱顶下沉减少30%左右。说明短锚杆随着施工推进,逐渐发挥对变形的控制作用,但其控制效果需随开挖过程逐渐体现。
3.3 开挖方法优化
目前对于软岩大变形隧道开挖方法,多采用三台阶分部开挖,但三台阶开挖方法初支封闭距离长,对围岩形成多次扰动,施工空间小,不利于长锚杆施工。同时由于软岩隧道变形量大,变形速率高,三台阶开挖成洞性差,如台阶连接处由于隧道变形造成钢拱架连接不密贴,喷射混凝土不密实等,造成结构受力薄弱,进一步加剧边墙变形。
为明确二台阶带拱仰开挖方法的变形控制效果,选取杨家坪隧道DK117+420—DK117+480作为试验段(中等大变形段),分别进行三台阶开挖方法和二台阶带仰拱开挖方法试验。分别对隧道变形、接触压力、拱架应力及锚杆轴力进行监测,测点布置见图9。

图9 测点布置
3.3.1 隧道变形
两种开挖方法下典型围岩变形时程曲线见图10。由图10可知,隧道变形受施工过程影响显著,变形呈台阶式增长,尤其当采用三台阶开挖时,中下台阶开挖时隧道变形速率明显增大。同时比较两种开挖方法的隧道变形过程,二台阶带仰拱开挖方法的变形收敛时间和变形量明显小于三台阶开挖方法。
3.3.2 围岩压力
初支与围岩接触压力时程曲线见图11。

图11 初支与围岩接触压力时程曲线
由图11可知,围岩接触压力受台阶开挖影响更加明显,三台阶开挖时尤其明显,受扰动影响,中下台阶开挖时围岩接触压力会出现减小现象,而二台阶带仰拱开挖方法下,围岩接触压力持续增长,当长锚杆施作后增长速率明显减小。虽然二台阶带拱仰开挖方法的围岩接触压力在前期较大,但由于长锚杆的及时施作,当初支封闭成环时两种开挖方法的围岩接触压力基本相当,但后期三台阶开挖方法的围岩接触压力仍保持较大速率的增长,造成最终围岩接触压力较大。
上述分析说明,二台阶带仰拱开挖方法对围岩的扰动较小,结构整体性更好,虽然由于变形释放较小,造成前期围岩接触压力较大,但由于长锚杆的及时施作,充分发挥了长锚杆对围岩的支护作用,最终围岩接触压力较小,初支与围岩接触压力包络图见图12。图12中,括号内外数值分别为两台阶带仰拱法和三台阶法开挖时初支与围岩接触压力值。

图12 初支与围岩接触压力包络图(单位:MPa)
3.3.3 钢架应力
型钢拱架应力时程曲线见图13。由图13可知,拱架承受压应力。三台阶开挖时,拱架应力增长波动明显,尤其是当中台阶开挖时拱肩部位应力变化明显。二台阶带仰拱方法开挖时,拱架应力随开挖进程持续增长,但长锚杆施工完成后边墙部位拱架应力增长速率明显减小。从最终结果来看,二台阶带仰拱法可以减小拱架上部应力,增大边墙及仰拱应力,充分利用拱架承载力,控制边墙位移。
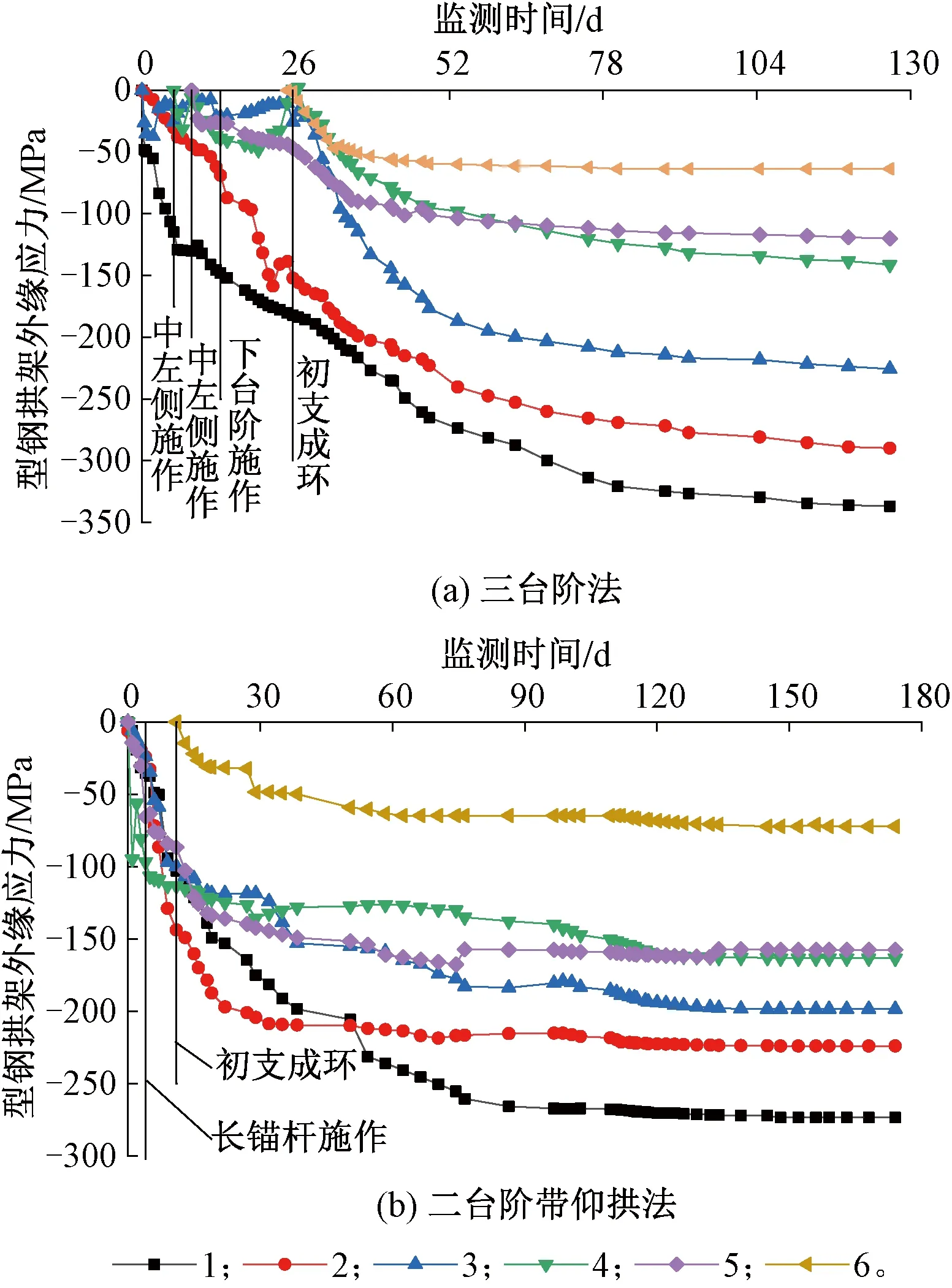
图13 初支型钢拱架应力时程曲线
3.3.4 锚杆轴力
边墙锚杆轴力时程曲线见图14。

图14 锚杆轴力时程曲线
三台阶开挖方法下锚杆轴力在施作后快速增长,但在下台阶、仰拱开挖时出现明显减小,说明台阶开挖扰动的作用阻碍了锚杆控制作用的发挥。而二台阶带拱仰开挖时,锚杆施作后轴力持续增长,受后续施工影响较小。同时比较两种开挖方法,初支封闭时锚杆轴力,二台阶带仰拱开挖方法明显大于三台阶开挖方法,说明锚杆发挥了更大的控制作用。这也是虽然二台阶带仰拱法应力释放较小但是结构受力较小的重要原因。
3.4 二次衬砌施作时机[52]
二衬结构安全性是软岩隧道面临的重要难题,而二次衬砌施作时机对结构安全性具有重要影响,同时也是反映软岩隧道主动支护理念的重要方面。
由于软岩具有显著的流变特性,其流变荷载具有明显的时间效应,考虑隧道施工过程,大部分流变荷载将由二衬承担。虽然在大变形隧道实践过程中也不乏通过提前施作大刚度二衬控制围岩变形的成功案例,但这与大变形等级、岩体挤压程度相关。同时大刚度二衬控制围岩变形与抗放结合的主动控制理论不符,科学性及经济性较差。
基于茂县隧道1#斜井未施作二衬的隧道变形长期监测结果见图15,目前的变形主动控制手段可以使围岩变形达到阶段性稳定,但如果长时间未施作二次衬砌,柔性初期支护会由于流变荷载发生承载力下降,变形加剧现象。结合主动控制的大变形控制理念,认为二衬可以在初期支护达到第一稳定阶段后施作,这样既可以通过有效控制的位移释放,减小二衬受力,同时又可以利用二衬的大刚度控制围岩流变。

图15 茂县隧道1#斜井变形时程曲线
基于实测变形数据统计,以初期支护变形达到第一稳定阶段变形量95%对应的变形速率作为二次衬砌施作变形速率标准,以不同大变形等级统计结果的80%保证率确定二次衬砌施作时机。对达到二次施作速率标准的时间进行统计,确定不同大变形等级下隧道二衬施作时间,进一步方便现场实际应用,隧道变形稳定时间(ti)正态分布曲线见图16。最终成兰铁路软岩隧道二次衬砌施作标准见表6。

图16 隧道变形稳定时间正态分布曲线

表6 成兰铁路软岩隧道二衬施作标准
3.5 型钢拱架
目前国内隧道拱架多采用格栅拱架和型钢拱架,其中格栅拱架与混凝土黏结性好,具有较好的受力性能,型钢拱架刚度大,支护力强。为探明不同拱架类型的作用效果,在茂县隧道1#斜井的严重大变形段开展了格栅I20b、I20b+I20b、H175三种类型拱架的现场试验,其变形时程曲线见图17[46,51]。

图17 不同类型拱架变形时程曲线
由于H175型钢拱架刚度大,从变形速率和变形量来看,明显优于其他两种类型的拱架。由此可知,增大支护刚度,可以有效控制围岩变形。但支护刚度增大,初期支护所受荷载明显增大,因此,针对不同大变形等级,应逐步提高初期支护中拱架的刚度,既可以有效控制围岩变形,又可以适当进行荷载释放。
同时,随着大变形等级的逐渐提高,型钢拱架破坏不仅表现为横断面的弯折,而且表现为纵向的失稳,因此,为加强拱架的整体性,采用工字钢加强拱架的纵向连接。
3.6 工艺优化
现场试验过程中,针对大变形特点,提出如下施工工艺优化:
(1)优化超前支护布置
超前支护是保持掌子面稳定,保证施工安全的重要手段。软岩隧道不仅拱部围岩稳定性差,而且边墙也常出现围岩剥落、掉块等情况。因此,将目前常用的拱部120°超前支护扩大为180°。
(2)锁脚锚杆布置优化
锁脚锚杆布置以径向方式施作,并在边墙钢架分布式施作,对保证钢架的整体稳定,防止钢架局部失稳起到了较好效果,锁脚锚杆优化见图18。
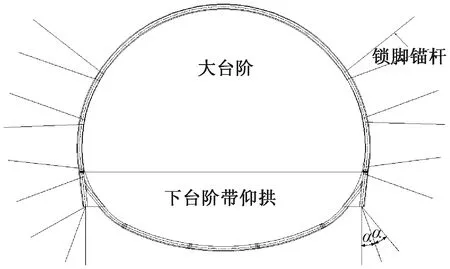
图18 锁脚锚杆优化
(3)锚杆垫板优化
随着锚杆加长,开挖工法优化,锚杆所受轴力不断增大,现场出现了锚杆与垫板、螺帽不匹配问题,锚杆破坏以螺帽拉脱,垫板凹陷为主。因此现场采用加大加厚的锚杆垫板,垫板边长为20 cm,厚度为1 cm。
3.7 施工机械配套
前期我国隧道机械化配套施工的目的主要集中于提高施工进度,改善作业环境等,随着施工技术的不断提高,围岩变形机制研究不断深入,机械化施工不仅关系着施工进度、施工质量,而且对施工安全、变形控制效果更具有显著的影响。尤其对于软岩大变形隧道,必须主动支护围岩,在减少对围岩扰动的同时,主动改善围岩的应力状态是关键,因此,大断面开挖,长锚杆施作,及时支护是必然选择。而上述技术措施的实现,必然需要机械化配套施工[53-54]。
施工机械除常规的挖掘机、装载车、出碴车外,主要涉及到锚杆钻机、混凝土喷射机及拱架台车[43]。
在钻爆阶段,由于炮眼深度浅,数量大,可采用手持风钻进行施工,以数量换速度。但由于软岩隧道系统锚杆长度大,手持风钻工效低,拱部长锚杆施作角度限制大。同时由于进口锚杆钻机价格昂贵,为此课题组联合厂家研发了针对软岩隧道的锚杆专用钻机,不仅可实现360°全环施工,而且双臂同时施工,工作效率高,现场应用表明8 m长自进式锚杆的施作时间可控制在20 min以内。
软岩大变形隧道多采用大刚度型钢拱架,如I20b、HW175甚至H200型钢。随着型钢型号提高,拱架单位质量逐渐增大,不仅造成工人劳动强度大,而且单榀架设时间长。尤其采用上述大断面开挖方法时,双线隧道上台阶HW175型钢拱架的重量达10 kN以上,采用人工架设时难度极大。为此引进三臂拱架台车,增加拱架架设效率的同时,将上台阶拱架由5节改为3节,既减少受力薄弱环节又可以节省时间。
3.8 动态调整
虽然上述分析针对大变形等级提出了针对性措施,但由于地质条件的变异性,勘测技术的局限性,大变形分级预测技术的不完善性[1,55],在隧道勘察阶段及施工阶段,面对复杂多变的地质条件,很难快速、准确的判断大变形等级,进而采用针对性措施。
因此,成兰铁路针对软岩大变形隧道采用动态设计的理念,在勘察及施工前期大量实测资料的基础上,对大变形等级进行初步判定。在此基础上,结合施工过程中围岩揭露情况,埋深,已施工段结构变形及受力情况以及必要的试验测试数据,采用“多方会诊”,对大变形等级进行确认及短距离预测,及时调整施工方案,实现动态调整。
3.9 成兰铁路软岩隧道变形控制体系
基于上述研究,并参考一定的工程经验,成兰铁路软岩隧道变形控制体系见表7[42]。

表7 成兰铁路软岩隧道变形控制体系
4 基于施工过程的隧道变形特征
4.1 变形数据统计
基于上述变形控制技术,分别对大变形等级条件下单、双线隧道变形进行分类统计,变形监测项目分别为拱顶下沉A、边墙收敛S1和S2,其中S1-1、S1-2、S2-1和S2-2分别为S1和S2的位移监测点。由于断面型式、开挖方法较多,以双线隧道为例,S1位于拱肩,S2位于边墙,见图19。

图19 隧道变形量测点布置示意
单线铁路隧道轻微、中等、严重大变形段监测断面分别为153、96、68个,双线铁路隧道轻微、中等、严重大变形段监测断面分别为101、199、35个。极严重大变形段缺少统计样本。部分隧道变形分布见图20。
由图20可知,虽然对隧道变形进行了分类统计,但由于地质条件及施工条件的复杂性,隧道变形量具有较大的离散性,而且随着变形等级提高,离散性变大。如轻微大变形段边墙位移最小值为46.6 mm,最大值276.9 mm,相差约5.9倍;严重大变形段边墙位移最小值为66.2 mm,最大值为561.99 mm,相差近8.5倍。这主要是由于软岩隧道变形影响因素众多,大变形等级越高,地质条件、隧道支护措施及施工过程越复杂,导致隧道变形离散性越大。
4.2 隧道变形特征分析
4.2.1 典型变形时程曲线
典型断面隧道变形时程曲线见图21。由图21可知,三种大变形等级下隧道变形与时间密切相关,按隧道变形速率可分为快速增长阶段、持续增长阶段和缓慢增长阶段,并且大变形等级越高,快速增长阶段变形速率越大,变形振荡增长越明显,变形持续时间越长。同时隧道变形时程规律受开挖方法影响,边墙位移尤其明显,中下台阶开挖时,边墙位移速率明显增大,变形呈台阶式增长。

图20 单、双线隧道变形分布
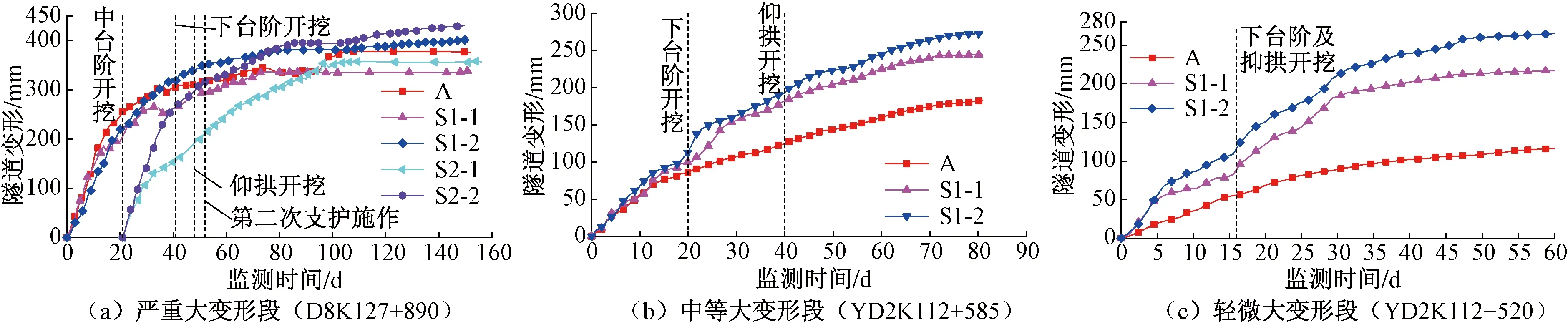
图21 典型断面变形时程曲线
4.2.2 各施工阶段隧道变形占比分析
结合施工过程,对各施工阶段隧道变形量与总变量的比值(变形占比)进行统计,其中单线隧道严重大变形段统计结果见图22。

图22 单线隧道严重大变形占比分布
由图22可知,严重大变形段各施工阶段隧道变形占比相对集中于某一区域内。隧道变形主要发生在上台阶施工期间,变形占比达到41.5%~47.3%,中、下台阶及仰拱施工期间变形占比逐渐减小。并且拱顶下沉在中、上台阶施工期间变形占比明显高于边墙位移,仰拱施工后变形占比低于边墙位移变形占比,因此,在隧道施工期间,前期应重点关注拱顶下沉变形,后期应加强边墙位移控制。最终不同大变形等级下隧道各施工阶段变形占比平均值分布见图23。

图23 隧道变形时空效应分布图
通过严重大变形段与中等大变形段隧道变形时空效应分布可知,随着大变形等级提高,隧道变形在上台阶施工期间变形占比减小,仰拱施工后变形占比增大,说明随着大变形等级提高,围岩流变性增强,隧道变形的时间效应更加明显。同时隧道变形的时空效应受开挖方法影响明显,轻微大变形段采用二台阶带仰拱开挖方法,开挖分步少,初支封闭时间短,变形释放更小,仰拱施工后变形占比更大。
同时比较发现,拱顶下沉与边墙位移的时空效应差别较大,边墙位移在仰拱施工后变形占比更大,时间效应更加明显,对变形控制不利,而隧道以边墙位移为主,因此以边墙位移为准,各施工阶段变形占比见表8。

表8 各施工阶段隧道变形占比
5 隧道变形控制基准
5.1 隧道变形量统计规律
虽然隧道变形量受各种因素影响具有一定离散性,但某一大变形等级下隧道变形相对集中于一定范围内,其分布服从统计学中的正态分布规律[56]。因此本文采用数理统计学方法对隧道变形数据进行处理,进而确定隧道预留变形量。
当分布函数中方差σ2未知时,由于样本方差S2是总体分布方差σ2的无偏估计,则
(3)
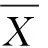
则隧道变形量平均值的置信水平为(1-α)的一个置信区间为
(4)
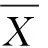

图24 隧道变形量区间估计示意
对上述隧道变形量统计样本进行分布规律显著性检验,并进行分布函数拟合,隧道变形量分布频数直方图及拟合函数见图25、图26。

图25 单线隧道变形分布直方图

图26 双线隧道变形分布直方图
由图25、图26可知,在显著性水平为0.05水平下,通过回归方程的显著性检验,虽然部分变形量级存在缺失,但某一大变形等级下隧道变形量统计数据显著性地来自正态分布总体。隧道变形量分布频数在某一范围内相对集中,通过分布拟合公式及置信区间的计算公式,隧道变形量平均值及95%置信区间上、下限见表9。

表9 隧道变形量置信区间计算结果 cm
由表9可知,随着变形等级的提高,隧道变形量平均值、95%置信区间上、下限不断增大,而且双线隧道变形量明显大于单线隧道。同时,随着变形等级提高,隧道变形由边墙位移为主向均匀变形过渡。如单线隧道轻微、中等和严重大变形段,拱顶下沉与边墙位移平均值的比值分别为0.56、0.89和1.03。这主要是随着大变形等级的提高,隧道埋深逐渐加大,地应力分布向静水压力分布规律变化,同时隧道断面向圆形过渡,边墙位移优势逐渐减小。
5.2 隧道预留变形确定
基于实测数据统计值,考虑量测丢失位移(15%)[42,57],取拱顶下沉的下限和边墙边移的上限,参考其他工程经验,对统计结果进行适当调整。其中极严重大变形段缺乏统计数据,但为与大变形分级相对应,根据隧道变形量随大变形等级提高而逐渐增大的规律,取严重大变形段隧道预留变形量上限作为极严重大变形段预留变形量的下限,最终成兰铁路软岩隧道预留变形量见表10。

表10 隧道预留变形量建议值 cm
5.3 基于施工过程的变形控制基准
上述预留变形量为隧道变形控制总量,但隧道变形随开挖逐渐增大。根据上述各施工阶段变形占比分析,当地质条件、支护参数及开挖方法确定时,某一施工阶段变形量与总变形量的比值相对集中于一数值。即以预留变形量为隧道变形控制的总基准,当某一阶段累计变形占比超过总基准的一定变形比例,则推测隧道最终变形量可能会超过预留变形量,造成初支侵限。以严重大变形段为例进一步说明,隧道采用三台阶法开挖,根据图23及表8可知,大量数据统计结果表明,当中台阶开挖至监测断面时,S1-1及S1-2变形占比平均值为42.4%。如监测断面S1-1或S1-2在中台阶开挖前变形占比大于42.4%,则根据变形随台阶开挖的发展规律,在不采取其他措施的情况下,当隧道开挖完成后最终变形量会超过预留变形量。同时当下台阶开挖时变形占比超过中、上台阶开挖时累积变形占比68.4%时,则最终变形量极有可能超过预留变形量。
基于上述思路及不同大变形等级下隧道施工过程变形规律,将边墙位移作为控制目标,以预留变形量为总基准,以施工阶段累计变形占比作为过程控制基准,成兰铁路软岩隧道位移控制基准见表11,其中极严重大变形段参考严重大变形段。其中轻微大变形段采用二台阶带仰拱开挖方法,中等大变形段采用二台阶开挖方法,严重与极严重大变形段采用三台阶开挖方法。

表11 基于施工过程的隧道变形控制基准
隧道大变形应进行过程干预,分阶段控制,表11的意义在于施工过程中通过监控量测对隧道变形进行预测,在隧道变形即将达到阶段变形标准前及时采取措施,从而有效控制隧道变形,避免初支侵限的发生。
6 工程试验验证
6.1 工程验证试验段
为了进一步验证软岩隧道变形控制体系的适用性,业主单位联合设计、监理、科研及施工单位,开展了大变形控制工程试验验证。基于上述控制体系,分别选取杨家坪隧道、茂县隧道作为试验点,每个试验段长度为40 m,试验段具体信息见表12。

表12 工程应用试验段大变形分级结果
6.2 应用效果分析
以隧道变形为主要考察目标,各工程应用试验段典型断面变形时程曲线见图27。

图27 典型隧道变形时程曲线
由图27可知,隧道变形时程规律符合典型的快速增长-减速增长和稳定阶段的变化规律。但随着大变形等级提高,隧道变形量逐渐提高,变形稳定时间逐渐增长,变形在初支封闭后经历一定时间增长后逐渐趋于稳定。
以边墙收敛S2为目标,对试验段变形量进行统计,随里程分布见图28。单线轻微段、单线严重段、双线轻微段、双线中等段隧道边墙收敛最大值分别为389.4、896.0、481.2、575.5 mm,分别占预留变形量的97.40%、99.56%、96.24%、95.90%;平均值分别为339.6、698.0、417.2、507.0 mm,分别占预留变形量的84.90%、77.56%、83.44%、84.50%。单线严重段由于围岩条件的复杂性及三台阶法开挖的复杂性,变形离散性更大,边墙收敛平均值与预留变形量之比较低,其他三个试验段边墙收敛平均值与预留变形量之比均在80%以上。由此可知,隧道预留变形得到了充分利用,同时未出现初支侵限,隧道变形得到有效控制,支护效果良好。
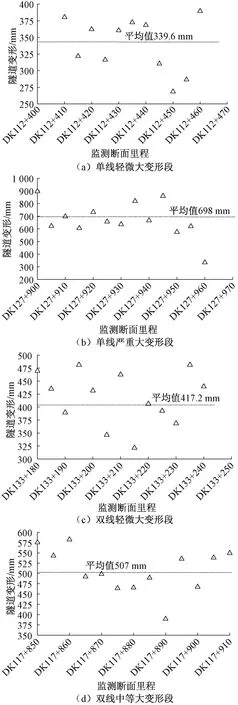
图28 隧道边墙收敛随里程分布图
7 结论
通过对成兰铁路软岩隧道变形控制技术总结和变形量测数据统计分析,提出软岩隧道变形控制技术及变形控制基准,得出结论如下:
(1)锚杆为控制软岩隧道变形的关键措施之一,宜采用全长黏结式锚杆,配备专用机械化设备,随大变形等级提高,逐渐增大锚杆长度,其中严重和极严重大变形段采用长短组合锚杆,实现锚杆的快锚固,早承载。
(2)针对不同大变形等级,逐渐优化隧道断面,尽量采用大断面开挖,既可以减少围岩扰动,又可以减少空间限制对长锚杆施作的影响,从而控制围岩变形,提高施工效率,二衬作为安全储备,在初支变形稳定后施作,保证结构的长期稳定性。
(3)基于主动控制的软岩隧道支护理念,成兰铁路提出“优化断面,强化锚杆,减少开挖分步,动态调整,分级控制”的软岩隧道大变形控制技术,现场应用取得了良好的效果。
(4)高地应力软岩隧道变形受岩体强度应力比及开挖方法影响明显,不同大变形等级下隧道变形量具有一定的离散性,但隧道变形量整体服从正态分布,考虑爆破至变形监测采集时间段的丢失位移,基于95%的区间估计确定隧道预留变形量的方法具有较强的工程应用性。
(5)基于变形数据统计分析,建议成兰铁路轻微大变形段、中等大变形段、严重大变形段和极严重大变形段单线隧道预留变形量分别为10~20、25~35、35~45、大于45 cm,双线隧道预留变形量分别为20~30、25~40、40~60、大于60 cm。
(6)考虑大变形分级和开挖方法,基于隧道施工过程建立高地应力千枚岩隧道变形控制基准,通过监控量测实时监测隧道变形,及时采用措施,可以有效防止初支侵限。
