干燥数学模型和动态模拟进展
2022-04-13王伟民
陈 键,王伟民
(云南化工设计院有限公司,云南 昆明 650041)
干燥过程是一个复杂的传质、传热过程,不仅消耗大量能量,而且还会影响干燥品质,目前还很难依靠理论研究来解决这一问题。因此,国内外学者以干燥试验为基础,与理论相结合,来研究物料的干燥过程[1-3]。值得注意的是,实验室研究是以小份量的实验材料为基础,不能很形象的说明物料干燥过程中的内部情形。数学模型和计算机模拟为干燥器的设计以及干燥参数的设定提供了重要工具[4,6]。
1 假设的提出
根据传热传质的基本理论,用偏微分方程表示高温干燥时的物料干燥过程。假设无物料的干燥只发生在降速阶段,那么对于无相变干燥的数学模型作如下假设[6-7]:
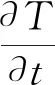
做出以上的假设之后,在进行干燥数学模型的建立以及运算方法的选择上就会很方便。
2 薄层干燥模型的建立
建立干燥模型时,对于物料内部水分的特性,通常依据薄层干燥方程做描述。薄层方程模型分为三类:扩散、半经验半理论和经验模型[8],而最具代表性的Newton方程和Page方程广泛的应用于农产品以及食品干燥行业,方程如下:
Newton方程:MR=exp(-kt)
(1)
(2)
对(2)取对数可得:
ln(-lnMR)=lnK+Nlnt
(3)
由此看出,lnMR 与t呈线性关系,根据经实验数据,可以应用Origin 7.0拟合方程或是最小二乘法回归求出相应的K的数值。
3 深层干燥模型的建立
深层干燥模型是以薄层干燥为基础,更深入的探究物料干燥过程,包括物料本身以及热空气的状态变化,为干燥工艺以及干燥参数的确定起到良好的指导作用。
3.1 深层干燥模型
基于在1中提出的6点假之外,对应的深层干燥物料做分薄层处理,而每一薄层都可应用薄层理论作运算[9-11],基本步骤如下:
1)把干燥物料在纵向上分为若干薄层n,每层的厚度为Δx;2)把干燥时间分为较短的时间间隔Δt,称为时间步长;3)把物料在横向上分成较小的距离间隔Δl,称为距离步长。有关系式如下:
Δl=v×Δt(v为物料传送速度)
(4)
4)进入第一层的热空气的湿含量以及温度为已知,经过规定的干燥时间后,利用薄层理论计算热风通过后第一层物料的水分含量;5)应用热质传到条件,计算热空气通过第一层后物料后的状态,即热空气的温度与湿度;6)干燥第二层时,以通过第一层物料的空气状态为基础,用同样的办法进行计算第二层物料的水分含量以及热空气的状态;7)重复上述计算,一直计算完所有料层为止;8)之后将时间增加Δt,物料向前移动Δl,进行步骤1)~6)的计算;9)重复步骤1)~8),直到达到物料干燥要求的含水率为止。
对于步骤3),给出以下解释:
如果物料在干燥过程中是以传送形式移动,利用上述描述进行计算;如果物料固定不动,则省略步骤3)。
3.2 偏微分干燥模型
在以上所述的基础之上,通过热质传递理论,建立偏微分方程如下:
1)质平衡方程
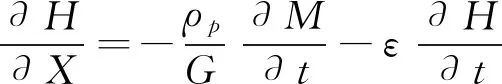
(5)
2)热平衡方程

(6)
3)热传递方程
(7)
4)干燥速率方程(或薄层干燥方程)
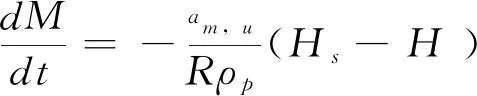
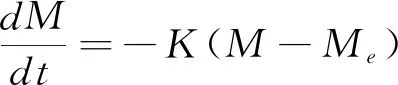
(8)
(9)
(10)
(11)
根据(1)、(8)、(9)、(10)四个偏微分方程,利用有限差分法可以进行求解,并且得到物料的温度、水分以及热空气的温度、湿度4个未知量。
3.3 模拟计算
模拟计算时,由于干燥装置的不同,有以下情况:
对于固定干燥床[12],可以把物料每一层作为一个节点,每个薄层物料的水分和温度以及热空气的温度和湿度用双下标表示。第一个下标表示薄层高度位置,第二个下标表示时间。
对于传动干燥床[11],可以把物料每一层作为一个节点,每个薄层物料的水分和温度以及热空气的温度和湿度用双下标表示。第一个下标表示薄层高度位置,第二个下标表示时间,第三个下标表示横线移动距离。
根据空气流向,模拟可以从上或从下物料层开始,实际情况选择前差还是后差方法,再根据提供的干燥模型进行计算,直至完成整个计算。
对偏微分法方程进行差分离散[13-16](采用向前差分方法):
1)对于固定干燥床:
(12)
(13)
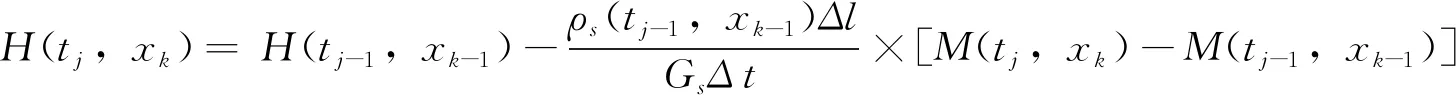
(14)
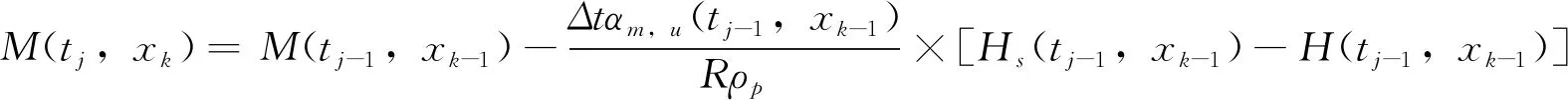
(15)
M(tj,xk)=M(tj-1,xk-1)-ΔtK(tj-1,xk-1)×[M(tj-1,xk-1)-Me] (降速阶段)
(16)
式(15)与(16)也可以用下式代替:
M(tj,xk)=Me-MR(tj,xk)×(M0-Me)
(17)
2)对于传动干燥床:

(18)
×{αh[T(li,tj-1,xk-1)-θ(li,tj-1,xk-1)] -
×[hfg+Cv(T(li,tj-1,xk-1)-θ(li,tj-1,xk-1))]}
(19)

(20)

(恒速阶段) (21)
M(li,tj,xk)=M(li,tj-1,xk-1)-ΔtK(li,tj-1,xk-1)×[M(li,tj-1,xk-1)-Me]
(降速阶段)(22)
式(21)与(19)也可以用下式代替:
M(li,tj,xk)=Me+MR(li,tj,xk)×(M0-Me)
(23)
对于以上的差分方程,还要考虑到允许误差,这里给出一个松弛因子ω,使得运算加快收敛[17]。
当然,其它所求量同样这样设定,使结果更为精确。
以上公式中:H为空气t时刻的湿度;Hs为物料表面空气湿度;M为物料的平均含水率;Me为物料平衡含水率;T为空气的温度;θ为物料的温度;cp为物料的比热容;cv为水蒸气的比热容;cw为水的比热容;ca为空气的比热容;ρa为空气的密度;ρp为物料的密度;k为物料干燥系数;a为单位体积物料的表面积;am,u为对流传导系数;h为对流换热系数;hfg为水蒸气的汽化潜热;G为物料流量;ε为空隙率;Ga为空气质量流量;Gs:为物料表面空气质量流量;Hvap为蒸发焓。
3)初始与边界条件
在初始值问题中,部分边界上的函数值和部分的函数偏导值是给定的。在初始值问题之中的独立变量值之一是时间t。在边界值的问题中,边界上的信息是给定的。
①一般干燥过程的初始条件[12]:
M=M0;θ=θ0;H=H0;T=T0
一般干燥过程的边界条件[18]:
边界条件的一般形式为:
(24)
G表示场域D的边界,为边界上的s的逐点函数。
三类边界条件如下:
第一类边界条件:φ|G=g(s)
(25)
(26)
第三类边界条件:(L含偏微商的算符;p,f为给定函数)
L≡-▽(p▽)+f
(27)
②一般干燥边界条件:
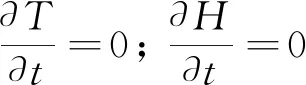
4)物料干燥过程模拟框图
模拟框图的建立,是实现计算机语言选择以及编程的重要前提[1,8]。在建立框图以前,基本的准备工作,包括数学模型、计算方法、相关参数和初始及边界条件要全部确定。干燥过程的基本模拟框图如1所示。
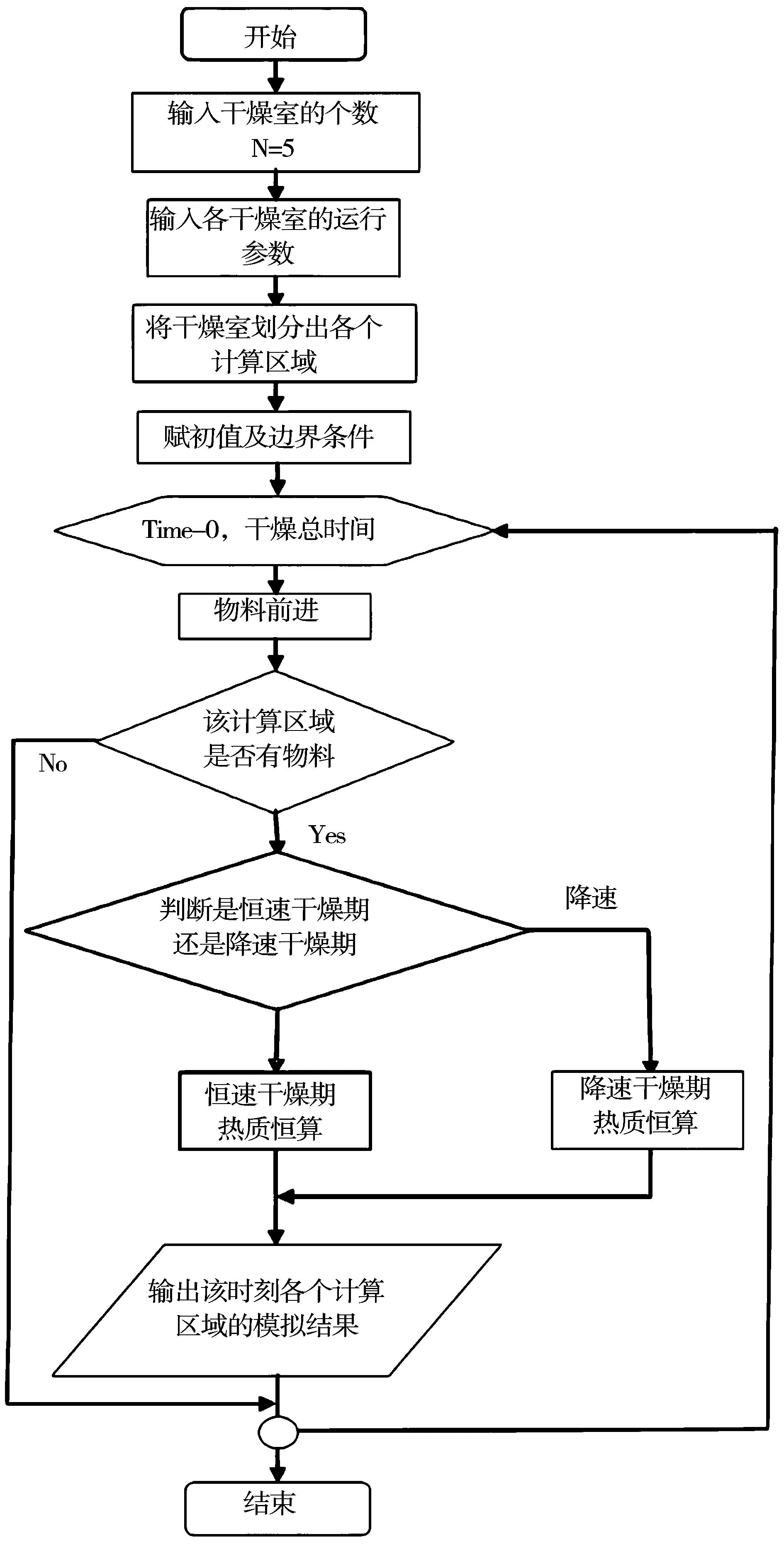
图1 基本模拟框图
4 干燥模型数据模拟结果分析
根据对物料干燥过程的动态模拟,所得数据与实验结果相对照,经过正交分析、方差分析以及最小二乘法对所得模拟数据拟合[11-13],并与所做实验结果相对比,若发现不足,对干燥模型的相关条件进行改正,使之模拟结果更加真实化。
5 结语
就目前干燥过程模型而言,基本都是以薄层干燥理论为基础,再进行对深层干燥过程的探究。通过基本的假设条件,对干燥过程做一理想化的模型,通过数值方法进行模拟,得到的数据具有借鉴性,据此做深入分析、整理,获取干燥过程过程最佳工况数据。因此,干燥过程模型的建立,一方面有利于实际干燥过程的参数的确定以及干燥设备的设计,另一方面也有利于干燥产品质量的提高。
