独塔对称自锚式悬索桥简化解析解研究

周德，张羽龙，王宁波，黄方林 ,周天睿

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中建七局投资有限公司，河南 郑州 450000)

自锚式悬索桥造型优美，跨越能力大，特别适用于地质条件受限且主跨在150～400 m 范围内具有景观要求的桥位。这种桥型主缆锚固在加劲梁上[1-2]，是一种自平衡体系，受力上也较地锚式悬索桥更复杂，其分析多采用基于有限元理论的数值仿真技术[3-5]。然而，对大型结构进行仿真分析，存在建模工作量大、修改模型繁琐和计算耗时久等不足，迫切需要一种简化且快速的计算方法。国内外许多学者对自锚式悬索桥计算理论上进行了大量研究。BATHE 等[6]把U.L 列式和T.L 列式进行了详细推导，但推导结果子矩阵较多，构造也比较复杂。杨孟刚等[7]基于U.L 的虚功增量方程，建立了一套完整的非线性有限元法，用于求解索力。黄琼等[8]基于能量法，提出一种计算两塔三跨自锚式悬索桥受力性能的简化计算方法，但其在求解时未考虑辅助跨的影响。王晓明等[9]将自锚式悬索桥分为主缆系统和塔梁系统，根据自锚式悬索桥自平衡体系及主缆的耦合特性，推导出简化解析公式，通过Newton-Simpson 方法求解，并和有限元计算结果进行对比。王邵锐等[10]考虑缆-梁联合作用的恒载状态计算方法，基于加劲梁的挠度理论，通过梁段的平衡微分方程、几何方程和物理方程推导出加劲梁的线形和索力的解析关系。刘超等[11]针对分段悬链线法收敛性能差、计算效率低等问题，提出了一种新的数值计算方法用于自锚式悬索桥主缆线形找形。向中富等[12]借鉴结构力学中位移法的求解思路，提出一种基于主缆内力状态计算吊索力的实用计算方法。上述研究多以双塔自锚式悬索桥为研究对象，专门针对独塔自锚式悬索桥的偏少。而在桥梁初步设计阶段，通常需要频繁修改设计，变更计算参数，工作量大，迫切需要一种快速求解的方法，使设计人员迅速了解参数修改后的桥梁受力状态。为此，本文根据独塔对称自锚式悬索桥的受力特点，提出一种基于最小势能原理的简化计算方法，并以主跨(150+150)m 九乔路自锚式悬索桥为算例，对该方法的适用性进行验证。

1 简化力学模型

1.1 力学模型

如图1所示，将独塔对称自锚式悬索桥在主缆和吊索处切断，桥梁分离为主缆体系和加劲梁体系，切断处主缆力和吊索力均用集中力来代替，分别为图中Fv和Fi(i=1,2,3,…,n)。

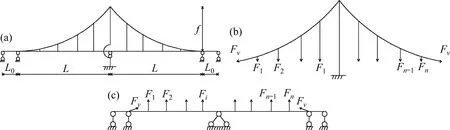
图1 独塔对称自锚式悬索桥简化力学模型Fig.1 Simplified mechanical model of a single-tower symmetrical self-anchored suspension bridge

1.2 基本假定

根据独塔对称自锚式悬索桥受力特点，理论推导时作如下假定：

1) 成桥状态在恒载作用下，桥梁保持“梁平塔直”线形，主缆线形为二次抛物线，吊索保持竖直状态；

2)加劲梁为等截面；

3)加劲梁和主塔之间采用简支约束。

2 成桥状态下内力和变形的简化解析解

根据成桥状态下“梁平塔直”的基本假定，可推导独塔对称自锚式悬索桥成桥索力和主缆力的解析解。

如图2所示，取加劲梁体系为研究对象，该体系主要受主缆力、吊索力和辅助跨传递的附加力，其中，qd为恒载折算的均布荷载；Hv和Hd对应主缆力的竖直分量和水平分量；m0，Qf对应辅助跨传递的附加力矩和附加力；若辅助跨跨度为L0，均布荷载为qf，则m0=qf/8，Qf=5qfL0/8。

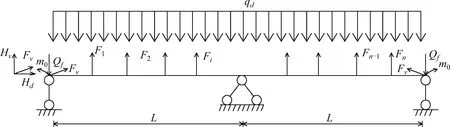
图2 成桥状态时独塔对称自锚式悬索桥加劲梁受力示意图Fig.2 Stiffening beam schematic diagram of the force in the completed state

忽略剪切变形产生的应变能，恒载作用下系统应变能为：

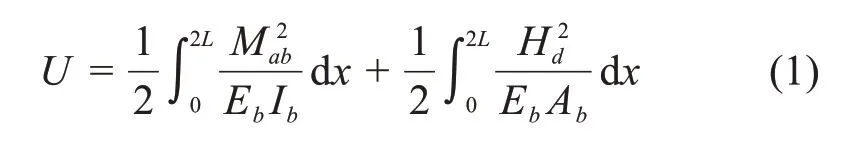
式中：Mab，Eb，Ib，Ab和L分别为加劲梁在任意截面的弯矩、弹性模量、惯性矩、面积和跨度。

若主缆单位长度重量为qc，则恒载作用下其承受的等效均布荷载q0为：

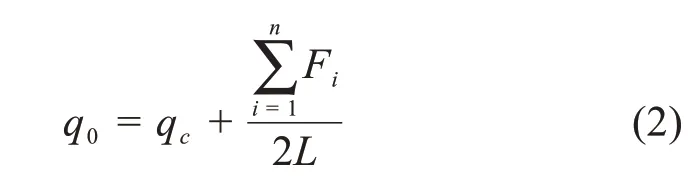
根据主缆线形为二次抛物线的基本假定，若矢高为f，则主缆水平分力Hd为：

加劲梁成桥状态时任意截面弯矩为：

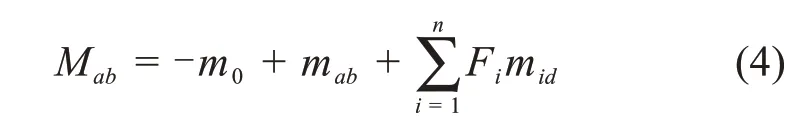
式中：mab为恒载qd，Fv和附加力Qf引起的加劲梁弯矩；mid为吊索力为单位力时引起的弯矩。

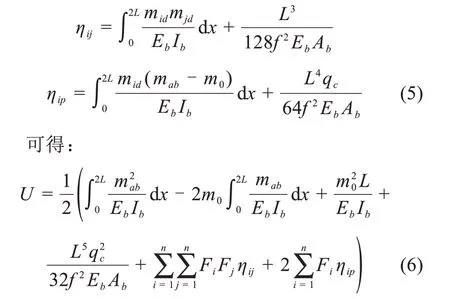
根据成桥状态时“梁平塔直”基本假定，δi=0，即：

根据卡式第二定理，

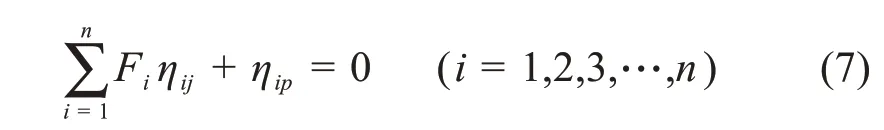
根据式(7)即可求出成桥状态时恒载作用下吊索力，再将吊索力代入式(2)和式(3)，可求出成桥状态时主缆的水平分力，进而求出主缆合力。

3 运营状态下内力和变形的简化解析解

3.1 恒载和活载作用下吊索力

如图3所示，运营状态在恒载和活载共同作用下，依然取加劲梁体系为研究对象，图中，q＇为恒载和活载折算而成的均布荷载，且q＇=qd+ql，ql为活载折算的均布荷载，pj为集中力，，，，Hb，和分别为恒载和活载共同作用下的吊索力、主缆力及其竖直分量、加劲梁轴力、辅助跨传递的附加力和附加力矩。

图3 恒载+活载作用下加劲梁计算简图Fig.3 Calculation diagram of a stiffening beam under dead load+live load

忽略剪切变形产生的应变能，恒载和活载共同作用下系统应变能为：

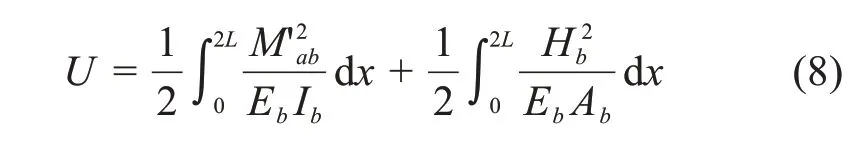
式中：为恒载和活载共同作用下加劲梁在任意截面的弯矩，其大小为：

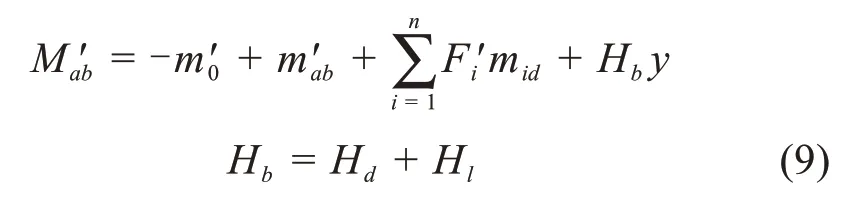
式中：为恒载、活载、主缆力和附加力共同引起的加劲梁弯矩；mid为吊索力为单位力时引起的弯矩；Hb为恒载和活载共同作用下加劲梁轴力；Hl为活载作用时主缆水平分力；y为加劲梁挠度；附加力矩m′0和前述m0计算方法保持相同。

根据卡氏第二定理，同理可求出恒载和活载共同作用下吊索力。

3.2 活载作用下主缆力

主缆在活载作用下产生的水平分力Hl可通过顺桥向变形协调条件进行求解，即加劲梁压缩量应等于主缆锚固点水平距离减小量。如图4 所示，取微小单元为隔离体，主缆长度为ds，荷载作用后长度为ds+Δds，du和dv分别为主缆水平投影增量和竖向投影增量。

图4 主缆微单元示意图Fig.4 Schematic diagram of the main cable micro unit

引入变形协调条件，可得：

式中：Ac为主缆横截面积，Ec为主缆弹性模量。

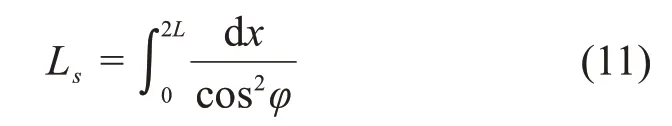
根据式(10)可求出活载作用下主缆的水平分力Hl。

3.3 恒载和活载作用下内力和变形的简化解析解

图5为恒载和活载共同作用下独塔对称自锚式悬索桥加劲梁受力示意图。图6为加劲梁解除主塔处竖向约束后由外荷载和支座反力引起的加劲梁挠曲线示意图。

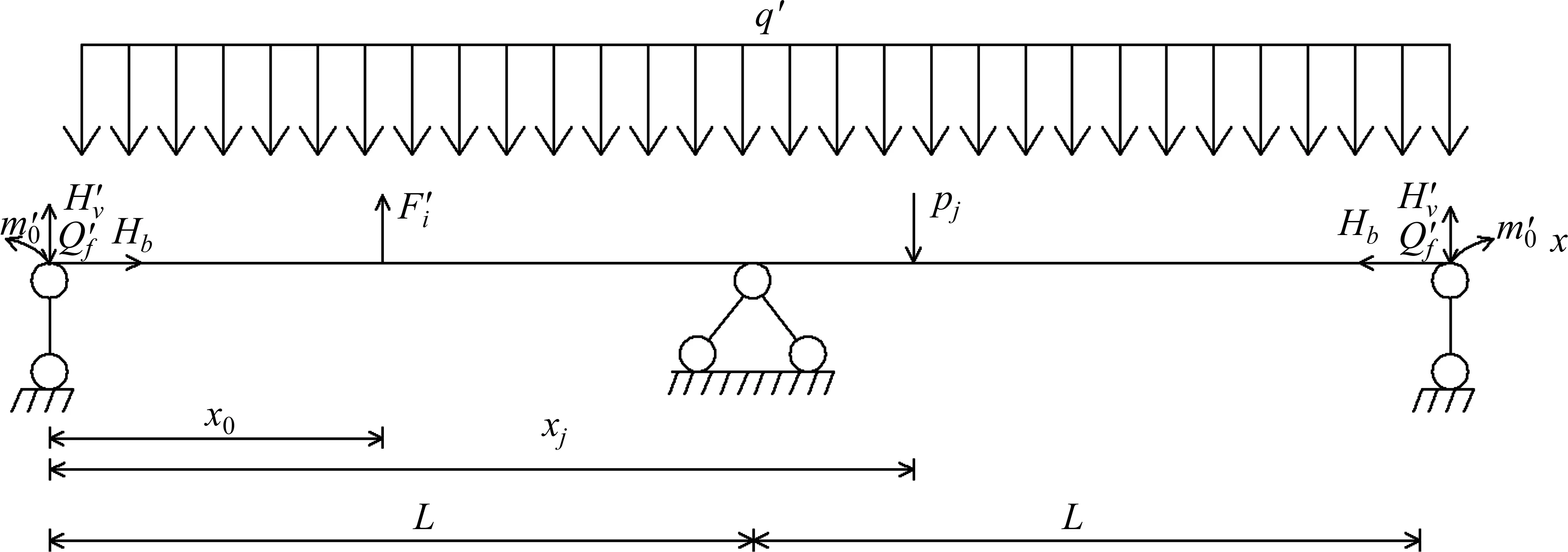
图5 恒载+活载共同作用下独塔对称自锚式悬索桥加劲梁受力示意图Fig.5 Stiffening beam schematic diagram of the force of a single-tower symmetrical self-anchored suspension bridge under dead load and live load

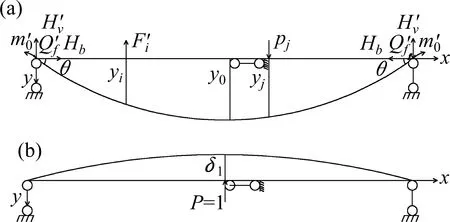
图6 大跨度独塔自锚式悬索桥加劲梁挠曲线示意图Fig.6 Schematic diagram of stiffening beam deflection curve of long-span single-tower self-anchored suspension bridge

忽略剪切变形产生的应变能，系统应变能为：

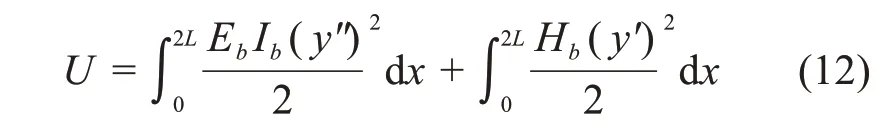
外力势能为：

式中：y为跨度2L的简支梁挠度；yj，yi分别为集中活载pj，吊索力位置处对应的挠度；θ为挠曲线两端的转角。

总势能为：

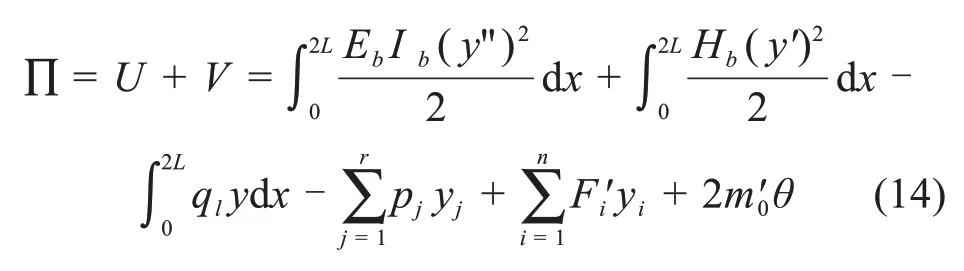
基于Ritz 法，解除支座后简支梁挠度y可用三角级数表示如下：

式中：am为待定系数。

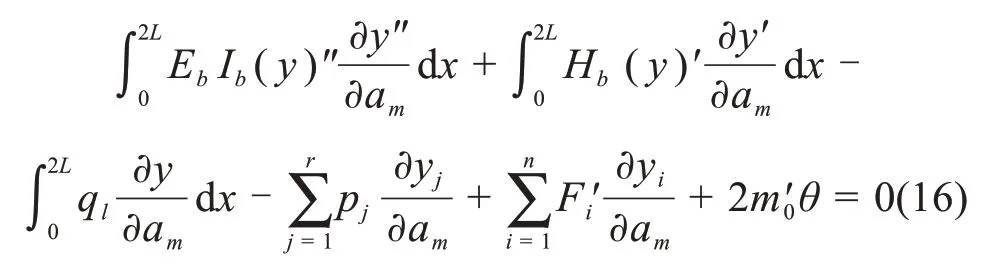
解方程并整理得：

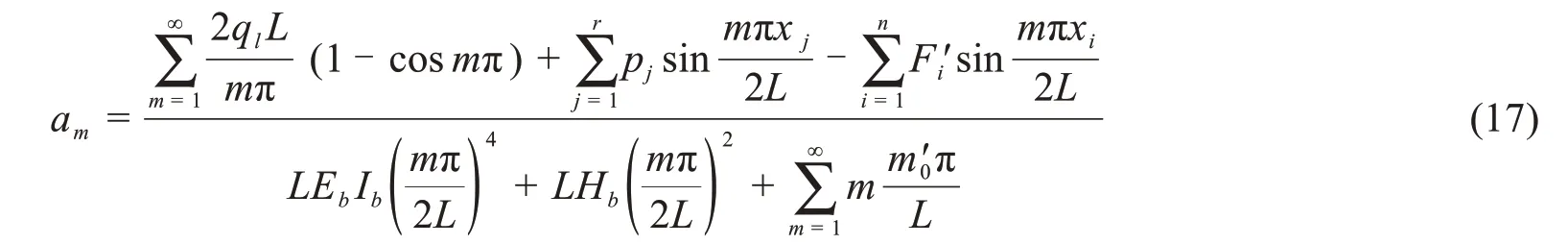
解除支座竖向约束后，简支梁在跨中处由恒载和活载共同作用引起的挠度y0为：

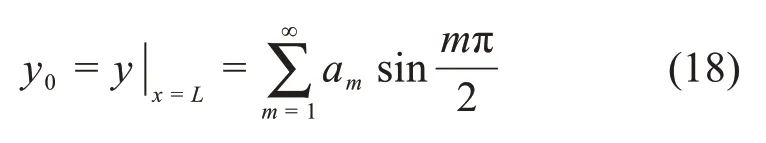
而作用在支座位置处单位力产生的挠曲线y1为：

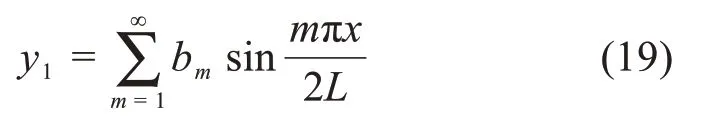
同理可得：

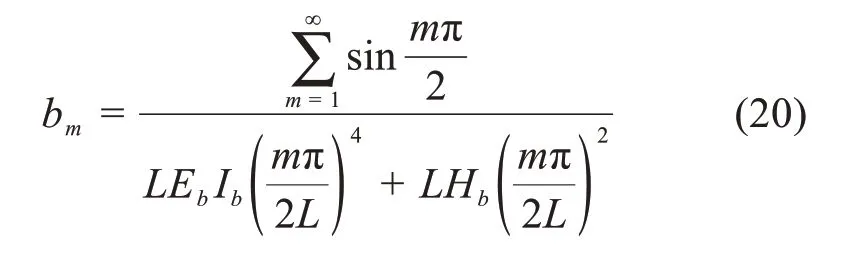
解除支座竖向约束后，简支梁在跨中处由单位力产生的挠度δ1为：

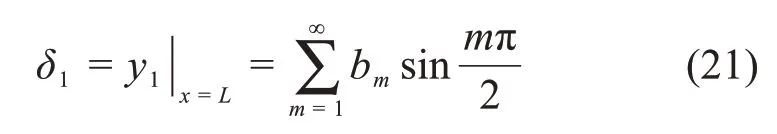
由支座处约束条件可得：

解方程得：

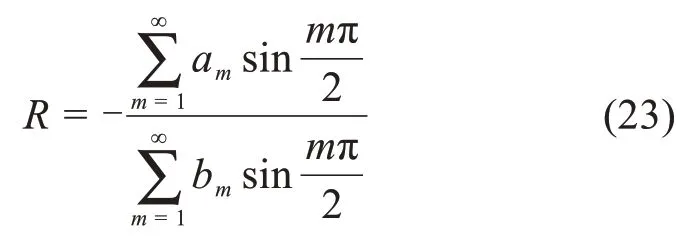
得到总挠度函数为：

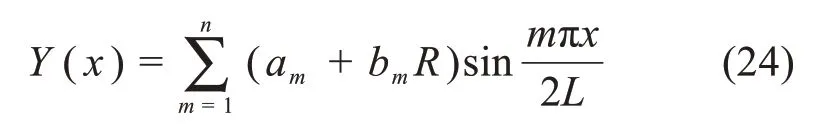
进而求出加劲梁弯矩如下：

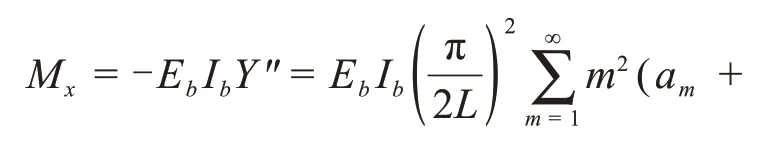
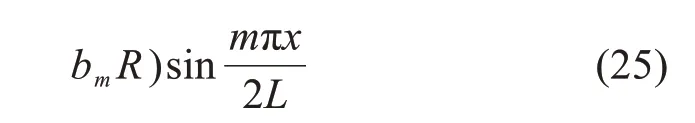
式(24)和式(25)即为含辅助跨的独塔对称自锚式悬索桥内力和变形的简化解析解，若无辅助跨则计算时m0和取零即可。

4 算例分析

4.1 工程概况

如图7 所示，九乔路独塔自锚式悬索桥全长368.4 m，跨径布置为30 m+2×150 m+30 m，桥面宽40 m，采用半漂浮体系。缆索为双跨双索面线形，理论跨径140.635 m，矢跨比为1/12。索塔高67.0 m，采用异型双柱式钢筋混凝土箱型结构，壁厚1.2 m。索塔基础采用矩形承台，长×宽×高为25.6 m×15.6 m×6.0 m。全桥设15 对吊索，吊索顺桥向标准间距为8 m，均采用高强度镀锌平行钢丝。

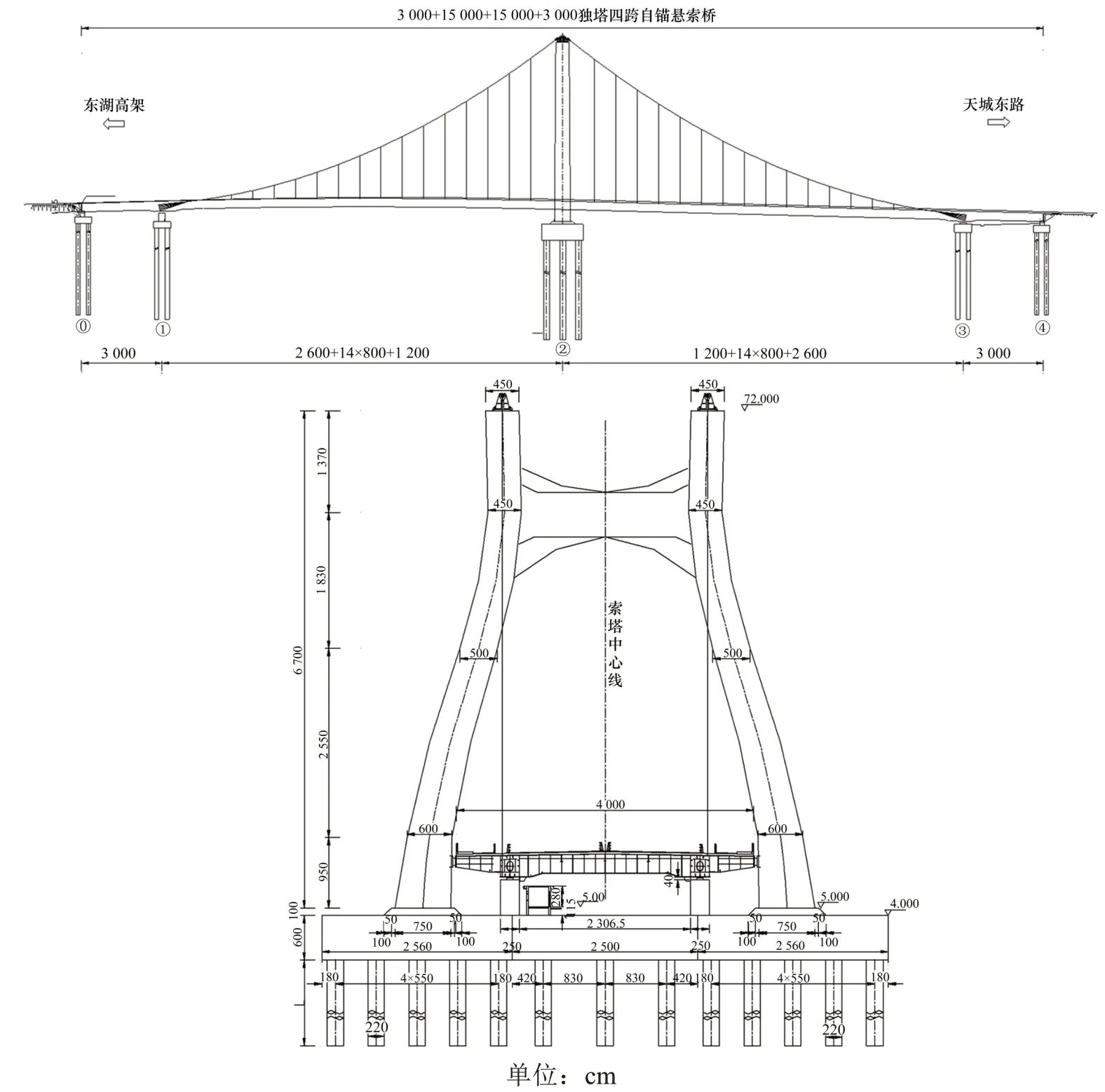
图7 九桥路大桥总体布置图Fig.7 Overall layout of Jiuqiao Road Bridge

材料参数取值如表1所示。

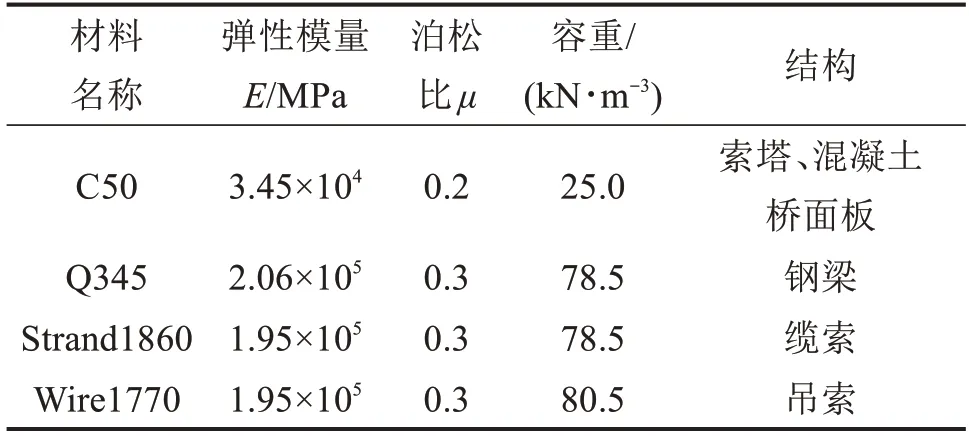
表1 材料参数Table 1 Material parameter

4.2 有限元模型

采用有限元分析软件Midas Civil 2020 建立九乔路自锚式悬索桥空间仿真模型。建模时，索塔和加劲梁均采用梁单元模拟，缆索、吊索均采用只受拉索单元模拟，混凝土板和钢板采用空间板单元模拟，通过调整缆索和吊索力确定合理成桥状态。边界条件按实际情况施加。全桥空间有限元仿真模型如图8所示。

图8 九乔路大桥有限元模型Fig.8 Finite element model of Jiuqiao Road Bridge

4.3 结果对比

基于本文推导的简化方法，采用MATLAB 编制程序，按照以下步骤求解：

1)对成桥状态进行分析，根据卡氏第二定理，求出恒载作用下吊索力和主缆水平分力；

2) 通过变形协调条件，求出活载作用时主缆的水平分力增量；

3) 根据卡氏第二定理，同理，求出活载作用时吊索力和主缆力；

4) 基于Ritz 法，根据最小势能原理，求待定系数，求解Ym；

5) 求解Ym+1，当∣Ym+1-Ym∣＜ε时(本文ε取0.001，此时m为21)，结束求解。

根据上述步骤对九乔路自锚式悬索桥内力和变形解析解进行求解，并与有限元数值解进行对比。图9 为成桥状态下索力对比图。图10 为双向6车道全桥满布静活载(公路I 级)作用下竖向挠度对比曲线。由图可见：2 种方法的计算结果吻合较好，索力最大偏差为11.12%，发生在吊索1处；竖向挠度偏差在15%以内。产生偏差的原因是简化解析解求解时加劲梁假设为等截面，与实际情况存在差异。

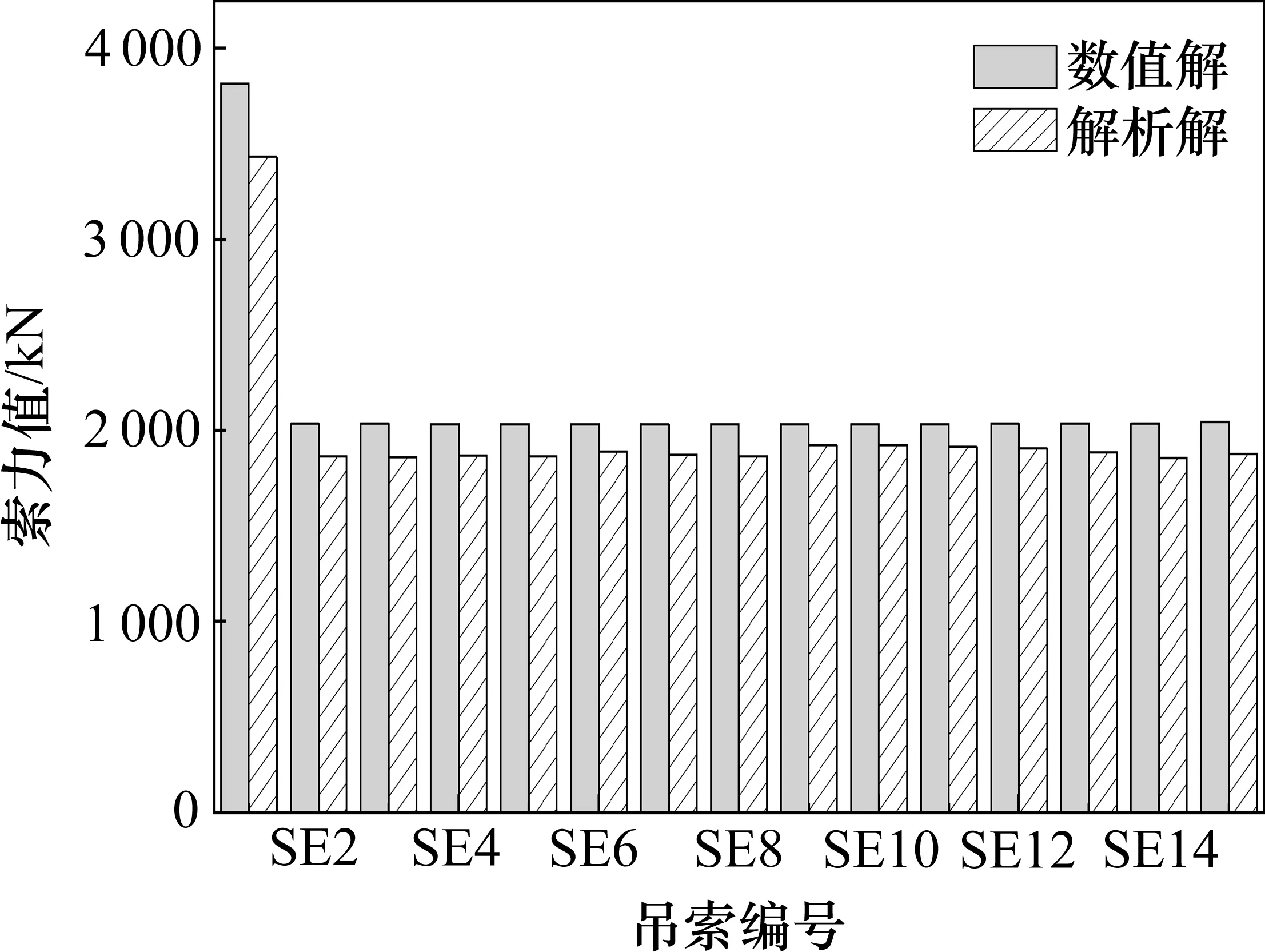
图9 成桥状态下九乔路大桥索力解析解与数值解对比(半桥)Fig.9 Comparison of analytical and numerical solutions of the cable force of Jiuqiao Road Bridge in the completed state(half bridge)

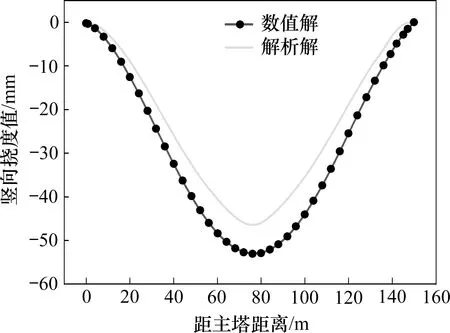
图10 活载作用下九乔路大桥挠度对比(半桥)Fig.10 Comparison of deflection of Jiuqiao Road Bridge under live load(half bridge)

5 结论

1) 基于最小势能原理，提出了一种求解独塔对称自锚式悬索桥内力和变形的简化解析方法。采用该方法对跨径布置为(150+150)m 的九乔路独塔自锚式悬索桥求解时，其计算结果与有限元仿真分析结果吻合较好，竖向挠度、弯矩和索力的分布规律基本保持一致，计算值2 种方法相差在15%以内，具备工程适用性。

2) 本文提出的简化解析解可为独塔对称自锚式悬索桥的初步设计阶段快速计算内力和变形及设计优化提供有益参考。

3) 本文提出的方法，未考虑非线性及刚度折减的影响，因此，对于跨度大于200 m 以上的独塔自锚式悬索桥，其简化解析解有必要做进一步的研究。