混凝土骨料周围水泥浆收缩裂纹形成机制

2022-04-13蔺海晓邵元元周淼

铁道科学与工程学报 2022年3期

蔺海晓，邵元元，周淼

(1.河南理工大学土木工程学院，河南焦作 454000；2.河南省地下工程与灾变防控重点实验室，河南焦作 454000)

混凝土是工程建筑中的重要材料之一，影响混凝土力学性能的因素很多，其中裂纹的影响尤为显著[1-3]，其中水泥浆硬化的干燥收缩引起混凝土由外向内的干缩变形裂纹，进而影响混凝土的健康发展，引起人们高度重视[4-5]。水泥浆硬化收缩会导致特征应力的变化，达到凝胶的抗拉强度时，将萌生裂纹。而特征应力是物体内一个或多个特征应变引起的自平衡力，不受任何其他外力和表面约束。众多学者对混凝土硬化过程中的收缩导致裂纹扩展问题开展了一系列研究。宋义敏等[6]以数字散斑相关方法对试验中采集的散斑图像数据进行分析,研究混凝土试件硬化过程中试件表面变形场演化特征。于本田等[7]开展了混凝土的早期收缩、抗裂和力学试验，并利用核磁共振仪和扫描电子显微镜对混凝土孔结构和微观形貌进行了测试，揭示抑制收缩开裂的机制。EGUCHI 等[8]将骨料、水泥浆作为混凝土两相，建立了混凝土硬化收缩预测模型，预测结果与试验测试值基本吻合。LI 等[9]基于毛细张力理论和混凝土微观孔隙，建立了自密实混凝土早期自收缩的预测方法。YOO 等[10]认为自收缩的起点应从应变和内部温度发生变化时开始，分别提出了考虑减缩剂影响的自收缩终值计算公式及预测模型。尹月明等[11]基于断裂力学理论得到界面层中弧形裂纹的应力强度因子，并根据复合型裂纹幂准则判断弧形裂纹是否发生开裂，进而来研究混凝土开裂强度的变化规律。SIRTOLI等[12]探究了ACI 209.R-92 预测模型的适应性，发现ACI209.R 模型虽然在干燥收缩方面模型计算值与实验结果吻合良好，但自收缩预测值与实验结果差异较大。为了预测混凝土硬化收缩产生微裂纹，将混凝土视为由线弹性球形骨料和均匀的线弹性水泥浆基体组成，建立了简单的线弹性预测模型，推导骨料中的特征应力状态[13]。但由于引起骨料周围裂纹的特征应力的大小和类型未知，这些模型的应用均受到了限制。因此，本文在采用环向传感器测试特征应力的基础上，通过光滑界面和完全结合界面断裂力学数理模型，数值分析裂纹扩展应力水平的上限和下限，并计算作为时间函数的预期裂纹扩展。

1 圆柱内特征应力测试

由于混凝土硬化过程中的收缩、刚度和黏弹性以不同速率变化，因此难以采用合适的数学模型对混凝土硬化的复杂过程进行预测。为了测得水泥浆收缩产生的特征应力，采用一种环向压力传感器，测试周围水泥浆收缩时环向压力传感器中形成的特征应力。

试验中使用高收缩水泥浆体，通过添加大量的硅微粉来增加硬化过程中的早强性，加快混凝土早期的自收缩，水泥浆的组分分别为水泥、硅微粉、水和超塑化剂，按120:24:36:1 的比例混合混合均匀。环向压力传感器放置在圆柱形模型的中心(如图1)，在传感器周围浇筑水泥浆，在水泥浆硬化过程中，通过环向压力传感器测试特征应力，如图2 所示，同时在显微镜(SAM-DENEB)下观测试件缺口处裂纹的萌生及扩展情况。

从图2 可以看出，大概在前16 h，水泥浆未出现裂纹，而大约22 h 左右，出现裂纹，而且随时间增加裂纹逐渐增长，大约115 h 时，裂纹形成并贯穿整个试件。试验中使用的水泥浆体硬化迅速，而且由于贯通裂纹是在超过100 h 形成的，因此在100 h的龄期内，弹性模量和断裂能几乎保持不变。为了便于后面断裂力学模型中的计算，采用Langmuir 函数关系对圆柱体中的测试压力进行曲线拟合，曲线拟合曲线如图2所示，拟合函数如式(1)所示，相关系数达0.979 3以上。

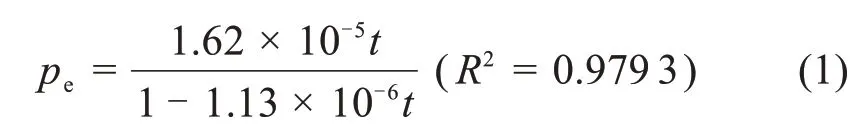
式中：pe为测试压力，MPa；t为时间，h。

嵌入水泥浆柱体中心的环向压力传感器承受水泥浆自由收缩(εmf)作用，对传感器的约束作用将产生夹紧压力。假定应力分布为平面，则传感器承受的压力(pe)在平面内是静压力，传感器上的压力将产生线性弹性应变(εs)，其应力-应变关系可表示为：

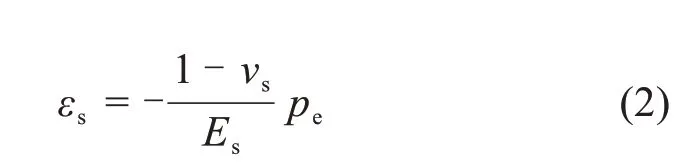
式中：Es和νs为传感器的弹性模量和泊松比。

在水泥浆和传感器界面的平衡条件下，传感器对水泥浆基体施加均匀压力，则水泥浆内部的应力可表示为：

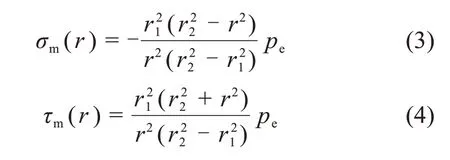
式中：r1和r2分别为传感器外径和水泥浆基体外径(如图1)；σm(r)和τm(r)分别为水泥浆内r位置的径向和切向应力。

将水泥浆基体的自由收缩率(εmf)与界面压力引起的弹性应变量(εm)叠加，得到水泥浆基体中的应力-应变关系：

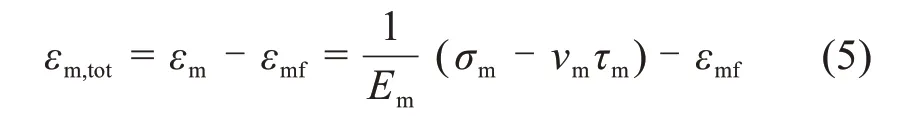
式中：Em和νm为水泥浆基体的弹性模量和泊松比。

考虑水泥浆基体和传感器界面(r=r1)的相容性(基体变形和传感器变形相等)，则：

求解给出平面应力条件下嵌入水泥浆收缩基体中的传感器内压力的线性弹性解：

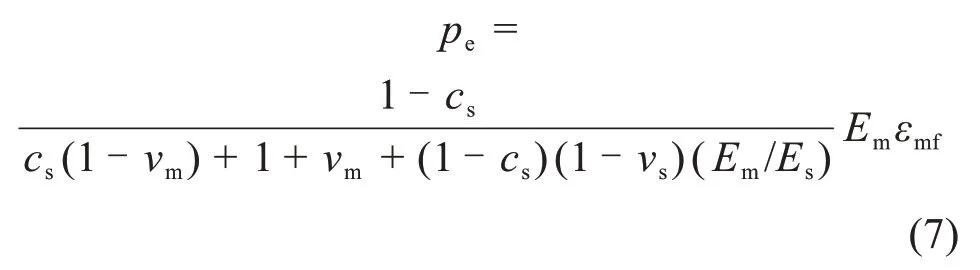
式中：cc为体积分数传感器体积相对于总体积的比值。

式(7)中水泥浆弹性模量和收缩率的乘积控制着压力，混凝土硬化过程中这2 种性能变化迅速。因此，在计算时必须对这些材料特性进行精确测试。应力传感器只能测量球体内部的应力，同时使用应力测量的结果以及式(7)中的线弹性解来估计其他几何形状中的应力。为此，引入了一个表示“有效刚度和收缩率(Emεmf)*”的参数。

当测得的特征应力与式(7)中的线弹性解相等时，有效刚度和收缩率的乘积可表示为：

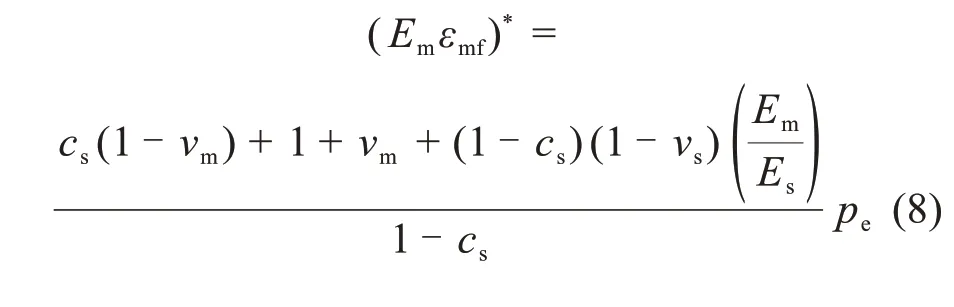
2 球内特征应力理论

在混凝土内部，骨料总是包裹在水泥浆内，在此，为了计算方便，假设骨料为球形，建立混凝土骨料水泥浆硬化过程的特征应力模型，如图3所示，其中，骨料半径为R1，周围均匀地包裹一层水泥浆，半径为R2。

图3 球形骨料水泥浆收缩特征应力分析模型Fig.3 Eigenstress analysis model of spherical aggregate and cement paste

球形骨料受水泥浆自由收缩率(εmf)的约束，将在球体内部产生压力(p)。压力与球形骨料的线弹性应变(εa)相关，在静压力状态，球形骨料的应力-应变关系可表示为：

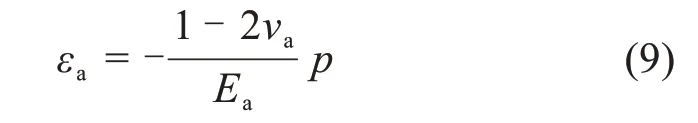
式中：Ea和νa分别为骨料的弹性模量和泊松比。

在水泥浆的内表面，需要一个均匀压力p来平衡，则水泥浆内部的应力可表示为[14]：

式中：σm(R)和τm(R)分别为水泥浆内部R位置的径向和切向应力。

水泥浆基体中的应力与弹性应变(εm)有关，水泥浆基体中的总应变与弹性应变和收缩应变的关系可表示为：

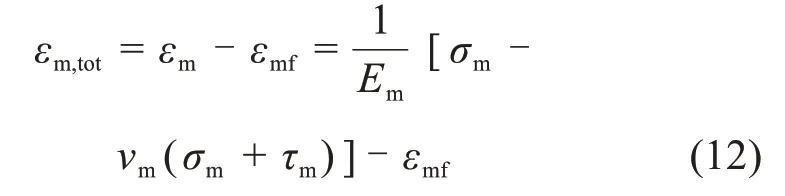
式中：Em和νm分别为水泥浆的弹性模量和泊松比。

在传感器和水泥浆界面处(R=R1)，应其相容性要求，则有：

通过求解上述方程，得到球内压力的线弹性解为：

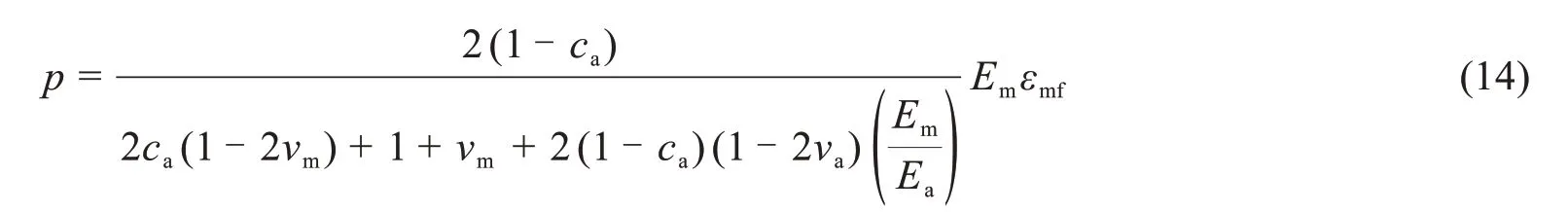
式中：ca为球体骨料体积与总体积(球体和水泥浆)的比值，。

将式(8)(有效刚度和收缩率的乘积)代入式(14)，即可得到水泥浆基体收缩中骨料的特征应力：

3 断裂力学模型

假设球形骨料附近存在裂纹尖端，由于水泥浆基体收缩作用在骨料上加紧压力是裂纹扩展的驱动应力。基于LEUNG[15]提出的2 种断裂力学模型进行水泥浆基体的断裂力学分析。该模型给出了裂纹尖端在加紧应力下的应力强度因子的上下界。通过将应力强度因子与水泥浆基体的临界应力强度因子相等来确定临界驱动应力，进而确定裂纹扩展的临界驱动应力。

基于2条裂纹在骨料两侧无限大水泥浆基体扩展的假设，特征应力p作为裂纹开口处的驱动应力，在此采用线弹性断裂力学模型。通过假设水泥浆基体和骨料之间的2种不同边界条件，分析临界应力强度因子的上限和下限(如图4 所示)[16]：1)假设水泥浆基体和骨料之间完全脱黏且无摩擦，推导临界应力强度因子的下限。2) 考虑水泥浆基体和骨料界面的完全结合，确定上限。

图4 断裂分析模型Fig.4 Fracture analysis model

对于光滑界面的应力强度因子(Ka)可表示为：

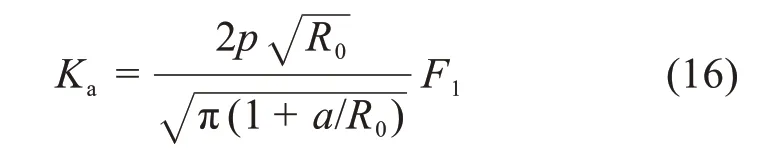
对于完全结合界面的应力强度因子(Kb)可表示为：

式中：F1和F2为裂纹长度a的函数，该长度a与骨料半径R0归一化处理。

为了使得2 个应力强度因子Ka和Kb易于比较，它们应具有相同类型的表达式，因此，引入2个依赖于归一化裂纹长度(a/R0)的裂纹长度因子Fa和Fb，进而分别得到式(16)和式(17)的新的应力强度因子表达式：

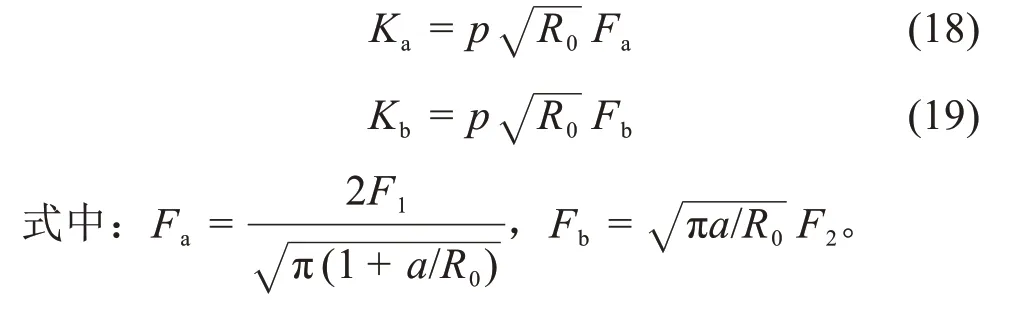
式(18)和式(19)表明边界条件的差异仅受影响因子Fa和Fb的影响。

当应力强度因子K大于或等于临界应力强度因子Kcr时，裂纹将扩展。临界应力强度因子是一种材料特性，用裂纹尖端平面应力的假设来确定：

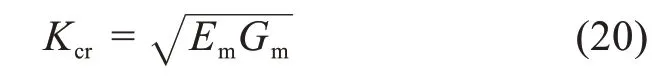
式中：Gm为水泥浆基体的断裂能。

当应力强度因子Ka和Kb与临界应力强度因子Kcr相等时，可获得裂纹扩展的临界驱动应力pcr，在该临界驱动应力作用下，靠近骨料的裂纹将进一步扩展到水泥浆基体中。通过式(18)～(20)，获得临界压力pcr的上限和下限。

对于光滑界面，临界压力成为裂纹扩展的下限压力(pcr-low)：

对于完全结合界面，临界压力成为裂纹扩展的上限压力(pcr-up)：

对于硬化基体材料，材料性能随时间而变化，因此临界压力也随时间而变化。

4 数值结果与分析

在假定传感器和骨料的性质相同的情况下，给定材料的物性参数如表1 所示，对式(15)中水泥浆材料性质的影响进行计算，结果如图5所示。

表1 材料物性参数Table 1 Material physical parameters

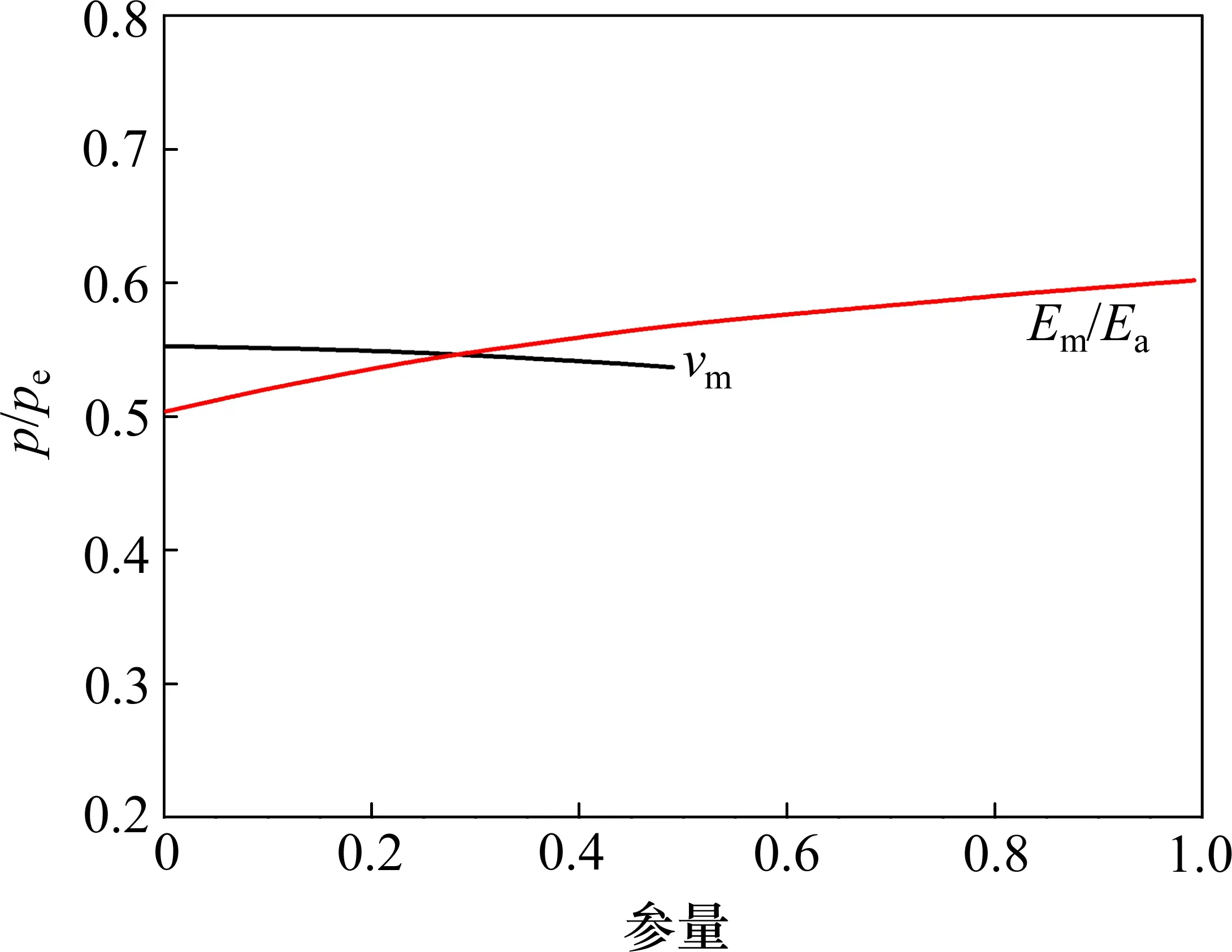
图5 材料参数变化特性Fig.5 Variation characteristics of material parameters

图5 为在表1 给定参数的情况下，根据式(15)计算得到的水泥浆基体参数变化对相对特征压力变化的影响。从图5中可以看出，水泥浆材料性能νm和Em/Ea对相对特征应力的影响非常有限。因此，这些特性参数的时间的依赖性和黏弹性对计算特征应力时的影响是无关紧要的，可以将其排除在分析之外。即通过使用与时间无关的线弹性材料特性和环形传感器中特征应力的测试结果，可以以合理的精度估算嵌入水泥浆体的骨料中的约束应力。

图6给出了裂纹长度因子随着归一化裂纹长度(a/R0)的变化规律。从图6 可以看出，对于0.01 到3的归一化裂纹长度，边界条件的差异导致因子F1和F2随着归一化裂纹长度变化趋势不同，F1随着归一化裂纹长度增大呈指数增大，而F2随着归一化裂纹长度增大呈指数减小[16]。这不仅使得应力强度因子的表达式(16)和式(17)不同，而且因子变化趋势也不同。为了获得相同形式的应力强度因子表达式(18)和式(19)，引入的裂纹长度因子Fa和Fb具有相同的变化趋势，仅定量上存在差别。图6还显示了归一化裂纹长度(a/R0)在0.64 和0.56 时2 个因子(Fa和Fb)的最大值(0.74 和0.45)，这种尺寸的裂纹很可能会进一步扩展到水泥浆基体中。

图6 裂纹长度因子与归一化裂纹长度的关系曲线Fig.6 Crack length factor on normalized crack length

假设水泥浆基体在超过100 h 时的临界应力强度因子为常数，并基于拉伸试验测试的水泥浆体的弹性模量和三点弯曲法测试的水泥浆体的断裂能(Em=22 GPa，Gm=5 N/m)[17]，可根据式(21)和式(22)计算得到随归一化裂纹长度变化的临界压力。在图7 中分别给出了水泥浆基体(R0=10 mm)和骨料在光滑界面和完全结合界面时临界压力随归一化裂纹长度增大的变化规律。从图7可以看出，临界压力对裂纹尺寸具有显著的的依赖性，当裂纹尺寸较小时，临界压力随裂纹尺寸增大急剧减小，在归一化裂纹长度在0.5～0.7之间达到极小值，当裂纹尺寸较大时，临界压力随裂纹尺寸增大缓慢增大。对于光滑界面，归一化裂纹长度为0.64 时，最小临界压力为4.46 MPa；而完全结合界面，归一化裂纹长度为0.56 时，最小临界压力为7.45 MPa。同时，同一归一化裂纹长度时，光滑界面时的临界压力均小于完全结合界面时的临界应力，即光滑界面时比完全结合界面更容易导致裂纹扩展。而实际界面的临界压力介于光滑界面和完全结合界面裂纹扩展所需临界压力之间。

根据式(1)和光滑界面模型和完全结合界面模型，裂纹扩展的临界时间随归一化裂纹长度的变化规律如图8 所示。根据图2 中的特征应力和图7中所示的临界压力，可以确定特征应力等于给定裂纹长度(a)的临界压力的临界时间。在图8中，分别给出了完全结合界面和光滑界面的临界时间与归一化裂纹长度的函数关系。并使用式(1)中特征应力关系式对临界时间进行了预测(450 h测试时间之后)。从图8 可以看出，在相同归一化裂纹长度时，完全结合界面的裂纹扩展临界时间远大于光滑界面裂纹扩展临界时间。同时，在归一化裂纹长度0.64 时，光滑界面在115 h 时裂纹扩展；而在归一化裂纹长度0.56 时，完全结合界面在673 h 时裂纹扩展。而且，对于完全结合界面，只有归一化裂纹长度在一定范围内，才存在裂纹扩展临界时间。总而言之，在水泥浆硬化过程中收缩时，水泥浆基体与骨料的完全结合界面难以导致裂纹扩展，而光滑界面更容易导致裂纹扩展，实际界面对应裂纹扩展难易程度介于完全结合界面和光滑界面之间。