悬挂式止水帷幕圆形基坑承压含水层地下水非稳定流计算

葛晓永, 张姝伊, 陈 征, 王旭东

(1.南京市江北新区中心区发展有限公司， 江苏 南京211816； 2.南京工业大学 交通运输工程学院， 江苏 南京 211816)

1 研究背景

基坑工程中常常采用止水帷幕控制地下水流动[1-2]，止水帷幕的设置改变了地下水流动的边界条件，加剧了基坑地下水流动的复杂性，给基坑地下水流动的定量计算带来了困难[3]，由此造成基坑降水设计的不合理。基坑工程中承压水易造成基坑突涌风险[4]，直接对基坑工程施工和周边环境安全产生影响[5]，现有的地下水计算方法无法满足设置了止水帷幕的基坑中承压含水层减压降水设计的要求。

Henry Darcy提出的达西定律奠定了地下水流动的理论基础，其后Theis[6]、Boulton[7]，Hantush等[8]依据地下水流动数学模型给出了理想条件下地下水流动问题的解析解，但这些理想模型的解析解无法满足分析基坑工程中复杂地下水流动问题的要求。基坑工程中常采用落底式和悬挂式两类止水帷幕控制地下水流动。落底式止水帷幕形成了地下水流动的隔水边界，含水层处于全封闭状态，吴林高[9]、高旭等[10]、王旭东等[11]、陈征[12]分别提出了矩形、条形、圆形区域隔水边界条件下的地下水水头降深解析解，为落底式止水帷幕基坑的地下水流动提供了计算方法。 受含水层分布、基坑开挖深度等条件的限制，悬挂式止水帷幕更为常见，止水帷幕的设置造成基坑地下水流动更为复杂，大大增加了地下水计算模型的求解难度。目前，悬挂式止水帷幕基坑的地下水流动计算主要采用大井法[13]，该方法在考虑止水帷幕对地下水流动的影响上存在局限性，为了解决这一问题，贺翀等[14]、彭祎等[15]、张志红等[16]对大井法进行了改进，利用水力梯度近似考虑止水帷幕对地下水流动的影响，拓展了大井法的应用范围。但这些方法都是基于地下水稳定流动的前提下建立的，无法反映基坑降水过程中含水层地下水的非稳定流动特性。

为了充分考虑悬挂式止水帷幕对圆形基坑中地下水流动的影响，反映地下水的非稳定流动特性，合理地开展悬挂式止水帷幕圆形基坑承压含水层的减压降水设计，本文通过建立悬挂式止水帷幕圆形基坑承压含水层地下水非稳定流动计算模型，利用Laplace变换和有限Fourier余弦变换，并结合Stehfest数值逆变换提出悬挂式止水帷幕圆形基坑地下水非稳定流的计算方法，以期为基坑工程中承压含水层的减压降水设计提供理论依据。

2 悬挂式止水帷幕圆形基坑地下水计算模型

悬挂式止水帷幕圆形基坑半径为a，坑内总抽水量为Q。承压含水层均质各向异性，厚度为M，承压含水层初始承压水头水平，止水帷幕插入承压含水层的深度为d，其计算模型如图1所示。

图1 悬挂式止水帷幕圆形基坑承压含水层地下水计算模型

鉴于悬挂式止水帷幕基坑地下水流动的复杂性，为了简化悬挂式止水帷幕基坑地下水流动的计算，忽略基坑内地下水流动和地下水流动引起的水头损失，以图1所示的承压含水层ABCDE区域中地下水流动为研究对象，将止水帷幕(AB)设定为地下水流动隔水边界，假设基坑抽水量与流过BC边界的流量相等，并以BC边界中点的水头降深表示基坑内承压含水层的水头降深。根据质量守恒定律和达西定律，以承压含水层水头降深表示的悬挂式止水帷幕圆形基坑地下水计算模型为：

(1)

式中：M为承压含水层厚度，m；d为止水帷幕插入承压含水层的深度，m；a为圆形基坑半径，m；Q为抽水井抽水量，m3/d；s为水头降深，m；kr、kz分别为承压含水层径向和竖向渗透系数，m/d；Ss为承压含水层储水率，m-1。

3 圆形基坑地下水计算模型求解

由悬挂式止水帷幕圆形基坑承压含水层地下水计算模型可知，承压含水层水头降深s(r,z,t)为空间坐标r、z和时间t的函数。为了求解上述计算模型，首先需将模型进行Laplace变换和有限Fourier余弦变换，推导Laplace空间的水头降深解。在此基础上，运用Stehfest数值逆变换求得地下水水头降深。

3.1 Laplace空间地下水计算模型

将承压含水层水头降深s(r,z,t)的Laplace变换映像函数[17]定义为：

(2)

式中：p为Laplace变换变量。

通过对计算模型式(1)的地下水流动方程和定解条件进行Laplace变换，Laplace空间的地下水计算模型为：

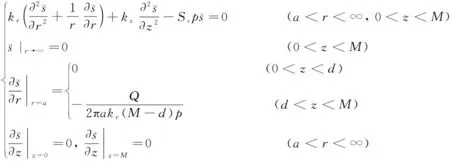
(3)

3.2 计算模型的有限Fourier余弦变换

在Laplace变换的基础上，通过对地下水计算模型式(3)中的自变量z进行有限Fourier余弦变换，将偏微分地下水流动方程转换为常微分方程，从而实现对地下水流动方程的求解。

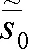
(4)

(5)

对于n=0和n≠0两种情况，模型式(3)经有限Fourier余弦变换得到的地下水计算模型分别为：

(6)

(7)

计算模型式(6)和(7)中的微分方程均为0阶虚宗量Bessel方程，其通解分别为：

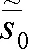
(8)

(9)

利用地下水流动区域边界条件，结合Bessel函数的性质[18]，当r→∞时，I0(r)→∞，K0(r)→0。通解式(8)和(9)的特解分别为：

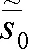
(10)

(11)

式中：K1为1阶第二类虚宗量Bessel函数。

3.3 Laplace空间水头降深解

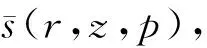
(12)

将公式(10)和 (11)代入公式(12)，可得到Laplace空间中悬挂式止水帷幕圆形基坑承压含水层的水头降深解为：

(13)

3.4 悬挂式止水帷幕圆形基坑地下水非稳定流解

因公式(13)无法直接通过Laplace逆变换求得水头降深解s(r,z,t)，只能通过对Laplace空间解的数值反演确定承压含水层的水头降深解。对于悬挂式止水帷幕圆形基坑的地下水流动问题，可采用Stehfest法[19]进行数值反演求得实际空间水头降深解s(r,z,t)，其计算方法为：

(14)

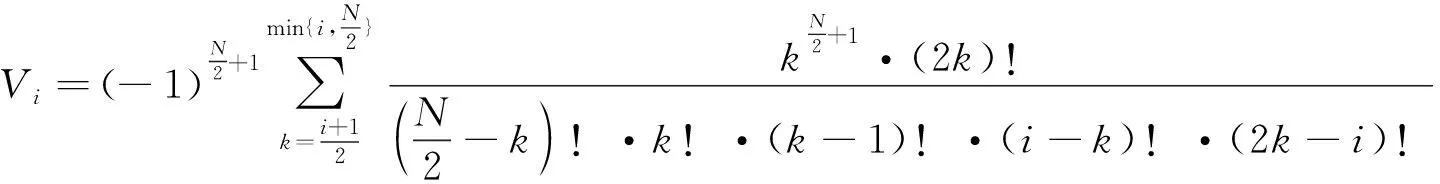
(15)

将公式(13)代入公式(14)中，可得承压含水层水头降深的半解析解：

(16)

公式(16)明确了悬挂式止水帷幕圆形基坑中承压含水层抽水量与承压含水层水头降深的关系，反映了止水帷幕对地下水流动的影响，为基坑工程承压含水层的减压降水设计提供了计算方法。

4 验证与讨论

4.1 水头降深半解析解验证

为了验证悬挂式止水帷幕圆形基坑承压含水层地下水非稳定流解的正确性，取a→0，地下水计算模型就转化为承压含水层非完整井的地下水流动问题。根据Bessel函数的性质，当a→0时，有：

(17)

将公式(17)代入公式(13)中，Laplace空间的解转化为:

(18)

公式(18)与Laplace空间无限承压含水层非完整井的地下水非稳定流计算公式[20]相同，由此验证了悬挂式止水帷幕圆形基坑水头降深Laplace空间解的正确性。

图2给出了悬挂式止水帷幕圆形基坑不同半径下减压降水时坑外承压含水层中水头降深(z=0)分布。由图2可见，随着圆形基坑的半径逐渐减小，水头降深逐渐逼近承压含水层非完整井的解答[21]，由此说明了Stehfest法在地下水非稳定流Laplace逆变换计算中的适用性和准确性。

图2 圆形基坑不同半径下坑外含水层水头降深分布

4.2 止水帷幕对基坑内外含水层水头降深的影响

基坑设置止水帷幕的目的是阻隔基坑地下水流动，图3为止水帷幕插入承压含水层不同深度时基坑外承压含水层水头降深(z=0)径向分布，图4为基坑内含水层水头降深与止水帷幕插入深度的关系。由图3、4可知，随着止水帷幕插入承压含水层深度的增加，坑外含水层水头降深逐渐减小，尤其是在2a(2倍基坑半径)范围内水头降深减小明显(图3)，有效减轻了基坑工程降水引起的周边环境效应；坑内含水层水头降深随着止水帷幕插入深度的增加而增大，在止水帷幕插入比d/M大于0.6时水头降深增大尤为明显(图4)，止水帷幕的设置减小了承压含水层的水头压力，有利于防止基坑突涌和保障基坑工程施工安全。由此可见，止水帷幕的设置对基坑内、外的地下水控制均起到了积极作用。

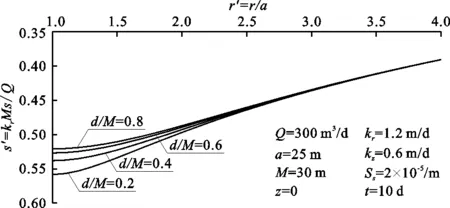
图3 止水帷幕不同插入深度时基坑外承压含水层水头降深径向分布

图4 基坑内含水层水头降深与止水帷幕插入比的关系

4.3 止水帷幕对基坑抽水量的影响

工程实践中基坑内承压含水层需维持一定的水头降深，以防止基坑突涌的发生。

图5给出了含水层在定降深条件下基坑抽水量与止水帷幕插入比的关系。图5中的计算结果表明，基坑抽水量随着止水帷幕插入含水层深度的增加而减小，尤其是当止水帷幕插入比d/M大于0.6时，基坑抽水量明显减小。止水帷幕在控制坑内外地下水流动的同时，也减小了基坑的抽水量。含水层水头降深、基坑抽水量与止水帷幕插入深度的变化规律可为工程实践中止水帷幕长度的优化设计提供参考。

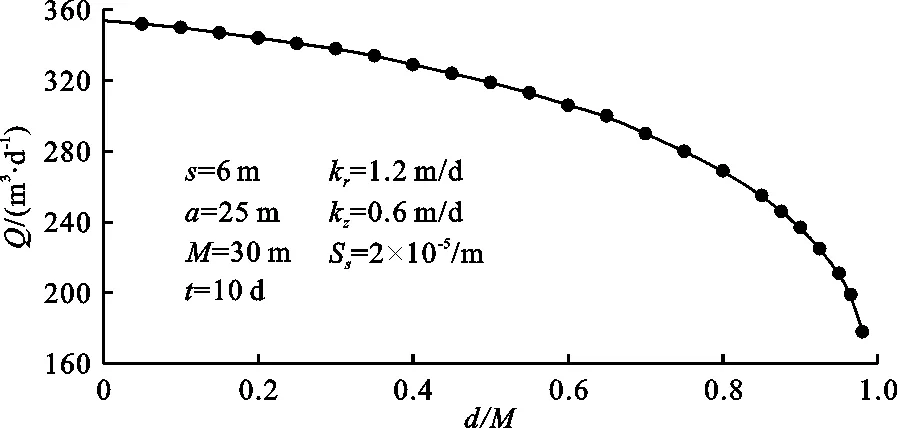
图5 基坑抽水量与止水帷幕插入比的关系

5 工程案例分析

5.1 工程概况

上海宝钢分公司三热轧工程旋流池圆形基坑采用地下连续墙围护结构[22]，旋流池基坑半径a=14.8 m，基坑开挖深度为35.3 m，地下连续墙入土深度为53 m。

场地主要分布有潜水和承压水，其中潜水赋存于①层杂填土和②1～③2层粉质黏土，③3层淤泥质粉质黏土、④层淤泥质黏土、⑤层粉质黏土为隔水层，承压水主要赋存于⑦1层砂质粉土和⑦2层粉砂，⑧1层粉质黏土具有较好的隔水性。将⑦1层砂质粉土和⑦2层粉砂合并为同一承压含水层，承压含水层厚度M约为26.7 m，地下连续墙插入承压含水层深度d=11 m，形成悬挂式止水帷幕。

旋流池基坑内设置4口降压抽水井(CH1、CH4、CH5、CH6) 和一口观测井G1，坑外有降压抽水井CH2，抽水井兼具观测井作用。基坑围护结构、降水井和观测井布置如图6所示。

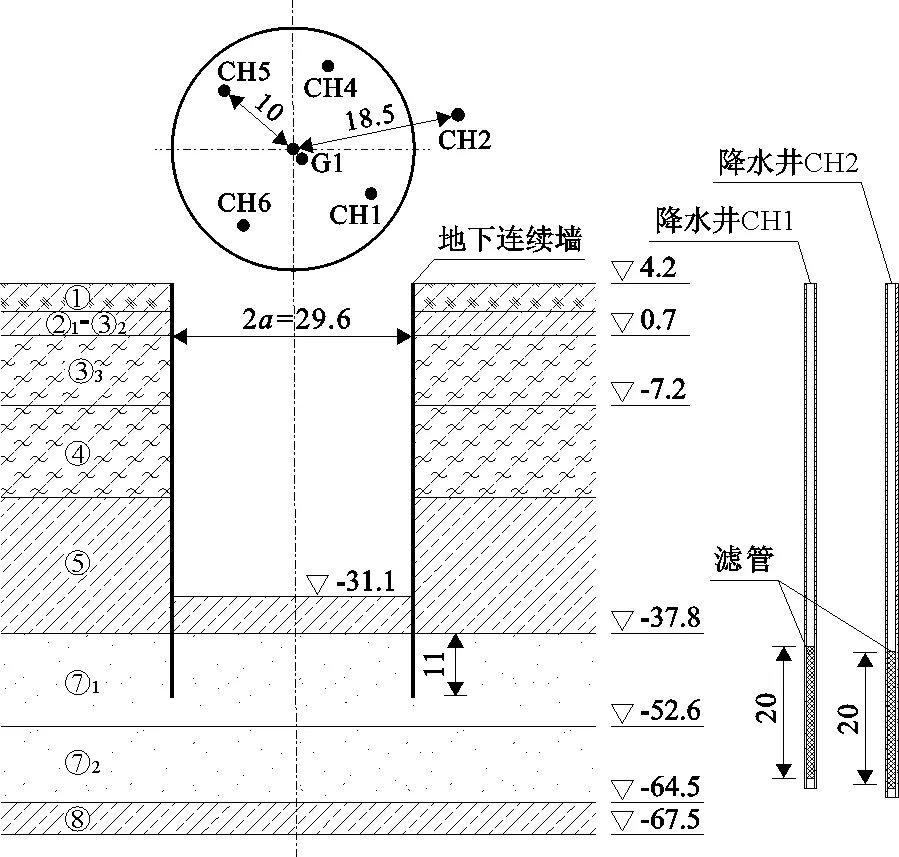
图6 案例工程圆形基坑围护结构、降水井和观测井布置(单位：m)

5.2 基坑现场抽水试验

根据坑外CH2单井现场抽水试验结果，求得⑦层承压含水层渗透系数k、贮水率Ss分别为0.85 m/d和1.62×10-4m-1。

为了验证悬挂式止水帷幕对地下水的阻隔作用，利用坑内抽水井CH1进行抽水试验，基坑总抽水量Q为17.9 m3/h，抽水时间t=24 h，测得坑内CH4、CH5、CH6、G1 4口井的平均降深为6.67 m，坑外观测井CH2的降深为5.46 m。

5.3 水头降深对比分析

为了验证悬挂式止水帷幕基坑承压含水层水头降深半解析解在实际工程中的适用性，对工程案例进行了计算分析，计算结果与实测水位降深对比如表1所示。

表1 案例工程承压含水层水头降深计算值与实测值对比

表1中计算结果表明，实测值和计算值之间具有良好的一致性，反映了悬挂式止水帷幕圆形基坑内、外承压含水层水头降深的分布规律。坑内水头降深的计算值较实测值小0.59 m，相对误差为8.8%，从工程实践角度，计算结果偏于安全，相对误差已能够满足基坑降水工程的实际要求，表明了悬挂式止水帷幕圆形基坑承压含水层地下水非稳定流计算方法的工程适用性。

6 结 论

(1)针对悬挂式止水帷幕基坑中复杂的地下水流动，提出了悬挂式止水帷幕圆形基坑承压含水层地下水非稳定流计算方法，计算方法考虑了止水帷幕的边界条件，采用数值逆变换实现了悬挂式止水帷幕圆形基坑地下水非稳定流的定量计算。

(2)计算分析表明，止水帷幕改变了基坑承压含水层的地下水流动，减小了基坑外含水层水头降深，加大了基坑内含水层水头降深，止水帷幕的设置有利于防止基坑突涌的发生和减轻基坑降水对周边环境的影响。当止水帷幕插入比d/M大于0.6时，止水帷幕对含水层地下水流动的影响明显，对基坑止水帷幕的优化设计有积极的意义。

(3)工程实例分析表明，计算结果合理反映了基坑内外承压含水层水头降深的分布规律，悬挂式止水帷幕圆形基坑承压含水层地下水非稳定流计算方法显示了良好的工程适用性，为基坑承压含水层的减压降水设计奠定了基础。