土坝渗压分析一元线性回归模型构建与应用
2022-04-12秦根泉苏晓林
秦根泉 田 慧 苏晓林
(1.四创科技有限公司,福建 福州 350100;2.福州大学土木工程学院,福建 福州 350100;3.福建省防灾减灾信息应用工程技术研究中心,福建 福州 350100)
大坝建成蓄水后,渗漏问题一直是影响大坝整体安全的一个重要因素。就土石坝而言,因防渗机理和筑坝材料特性的原因,大坝挡水渗流安全分析显得尤为重要[1]。前期,很多学者针对大坝渗流监测资料异常值成因分析、数据变化规律分析、安全监测系统研究及预测模型研究等展开了一系列的定性分析和工程实践验证,以此来评价工程的安全现状并推断未来变化趋势[2-4]。如雷艳等[5]基于实际工程特点建立考虑不同分区的有限元渗流分析模型,对水库土石坝进行了稳定-非稳定渗流分析,进而判断工程是否出现渗透破坏,为相似工程提供理论方法参考。吕高峰等[6]利用有限元分别计算测值异常增大前后的渗流场,并进行对比分析,以掌握测值异常增大对黏土斜心墙及渗流稳定的影响,为工程后期运行提供参考性意见。秦继辉等[7]将逐步回归模型(SRA)、小波神经网络模型(WNN)和基于逐步回归和小波神经网络的土石坝渗压预测模型(SRA-WNN)进行对比,得出在土石坝渗压预测中,前两种模型得到的预测误差均高于SRA-WNN模型,且建立SRA-WNN模型的输入因子更为合理,更能反映出大坝渗流状况。刘聪[8]结合工程实例,以土体渗透系数与土体体积应变之间的关系作为耦合的桥梁,用迭代耦合算法对该工程进行渗流与应力耦合分析,得出在工程设计时考虑渗流场和应力场耦合作用将会更加有利于提高土石坝体的安全性。王宇等[9]针对土石坝渗流安全预测预警,采用重标度极差分析方法(R/S分析),阐释了渗流时间序列具有分形标度不变性,揭示了渗流时间序列具有趋势性和随机性双重特性。
现有的研究偏重于对大坝渗流分析方法应用及特定的工程渗流安全问题进行分析,鲜有关于工程数字模型建立方法和应用效果的系统介绍。本研究依据东圳水库较为完整的大坝坝体渗压监测资料和统计学回归分析理论,对水库水位与渗压监测值的非确定性关系进行了公式推导,建立一元线性回归模型,实现了渗压值预测和水库安全允许水位控制的应用。通过对该工程29个渗压监测计的数据进行分析,得出了东圳水库大坝渗流监测相关性整体分析结果,并对该模型的可靠性和适用性进行了评价。
1 项目背景
东圳水库[10]位于福建省莆田市境内的延寿溪中游,是一座具有灌溉、防洪、发电、航运、养殖、游览等综合效益的大(2)型水利枢纽工程,防洪标准按1000年一遇洪水设计,10000年一遇洪水加20%校核,水库总库容4.35亿m3,电站总装机容量3台共计6320kW。该工程主要分为枢纽工程和渠道工程两大部分,其中枢纽工程由大坝、输水涵洞、溢洪道三部分建筑物组成。大坝坝型为黏土心墙坝,坝长367m,最大坝高58.6 m,顶宽8.34m,见图1。

图1 东圳水库大坝
东圳大坝于1960年建成,2014年除险加固时,建设了较为完备的变形、渗压和渗流监测项目。其中,渗压、渗流监测项目主要包括坝体渗流监测、绕坝渗流监测等。渗流监测在坝体设置了4个断面和左、右岸各一组绕坝断面,总共设置了29孔测压管,渗压监测项目基础信息见表1。测压管内监测数据于2018年4月25日始测,采用的是渗压计自动化监测,监测周期在运行初期为30min,正常运行期为8h。

表1 大坝渗压计编号信息
2 土坝渗压分析回归模型建立
2.1 数学模型建立方案
本文选取东圳水库大坝B0+090断面的渗压计BS3、BS4作为代表,通过收集、运用历史数据,研究模型构建方法并分析模型应用效果。建模过程包括数据预处理、建立数学模型、模型显著性检验。
2.2 监测数据预处理
2.2.1 数据预处理方法
前期研究表明,在一系列的大坝监测值中出现异常值是不可避免的。异常值对回归分析有显著影响,严重地影响对参数的估计,引起较大的残差,进而影响回归方程的拟合效果及预测预报性能[11]。常用的异常值统计检验法有拉伊达(3σ)、格拉布斯(Grubbs)、狄克松(Dixon)及t检验(3S,又称罗曼若夫斯基准则)等准则,均是以正态分布和小概率原理为基础的[12]。根据选取的数据特性,本文采用的方法是Grubbs准则。
根据Grubbs准则,服从正态分布的监测值序列若存在异常值,则有统计量
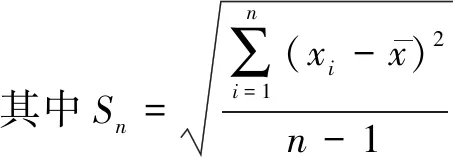
(1)

2.2.2 数据预处理结果
选取渗压计BS3、BS4各20组监测数据,根据上述计算公式,首先对渗压计监测数据进行预处理分析。采用Grubbs准则法对2个渗压计监测值和水库水位进行统一检验,得到其G统计量和临界值(显著性水平α=0.05),见表2。结果显示,仅2018年12月21日8时水库水位监测值的G统计量(4.25)大于临界值(2.56),检查发现,该数据对应的水位值为35.3m,低于水库死水位(50m),明显异常,应予以剔除。

表2 BS3与BS4号渗压计监测值与G统计量
2.3 建立数学模型
对于大坝渗流监控预报,目前出现了多种方法和模型,主要包括统计回归模型、时间序列模型、支持向量机模型以及神经网络模型等。其中,统计回归模型有着模型结构简单、参数少的特点,同时能够较好地处理非线性和高维数的问题,且在理论上得到的结果为全局最优。本文将大坝的坝体渗透系数、防渗措施、排水措施作为固定边界条件,水库水位作为大坝渗压值变化的唯一可变量,据此假定可建立水库水位和大坝渗压值的一元线性回归方程。
2.3.1 一元线性回归模型方程
假定存在一定关联性的两变量x与y,两者的关系是不确定的,则有一元线性回归模型的基本形式
(2)
式中:a、b、σ2是与x无关的未知参数;ε是不可预测的随机变量,且假定Eε=0,Dε=σ2。
又因ε为随机变量,则y也为随机变量,有
y~N(a+bx,σ2)
(3)
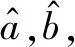
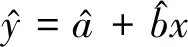
(4)
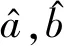
2.3.2 最小二乘法参数估计
针对x的一组不完全相同的值x1,x2,x3,…,xn做独立试验,得随机变量y的相应监测值y1,y2,y3,…,yn。因此,一元回归模型可以写为
(5)
若记
(6)

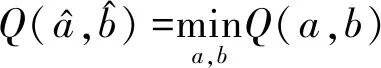
(7)
分别求Q(a,b)对a及b的偏导数,并令之为0,得
(8)
其中,根据样本数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),有
(9)
把(9)式代入(8)式,得
(10)
整理上述方程组,即得a、b最小二乘估计
(11)
即得y对x的回归方程

(12)
把xi代入式(12),有
(13)
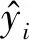
2.3.3 回归模型的显著性检验方法

(14)
相关系数R体现x与y线性相关程度。根据数据样本长度n和给定的显著性水平α(一般取值0.05或0.01),查临界值表可得临界值c。当|R|>c时,说明x与y两者存在线性相关关系;反之则说明x与y两者不存在线性相关关系。
2.3.4 回归模型建立与检验
根据上文预处理后的监测数据和建模方法,分别建立两个渗压计监测值与水库水位的一元线性回归模型,并根据式(14)对建立的模型进行显著性检验,结果见表3、图2。

表3 回归模型建立结果

图2 BS3与BS4号渗压计监测值与回归值比较分析
从表3可以看出,BS3和BS4渗压计的相关系数均在0.80以上,均大于临界值0.444,说明这两个渗压计监测值与水库水位存在显著的相关性;且由回归模型拟合得到的回归值基本符合监测数据的规律(见图2),说明以此建立的一元线性回归模型是有效的,可利用模型方程进行预测与控制。其中,确定的回归模型显示,渗压监测值相对水库水位变化的趋势是合理的,两者的变化斜率均小于1,分别为0.3500和0.3677,说明在渗流稳定的情况下大坝渗压与水库水位线性关系较为稳定。
3 应用回归模型预测与控制
3.1 模型预测方法
模型预测是指在大坝渗流稳定期,输入确定的水库水位值,对坝内某一具体位置的渗压值和变化范围进行预测。在获得经验回归方程后,对给定的x=x0,将x0代入经验回归方程,得
(15)
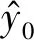

(16)
对于置信度1-α,可由
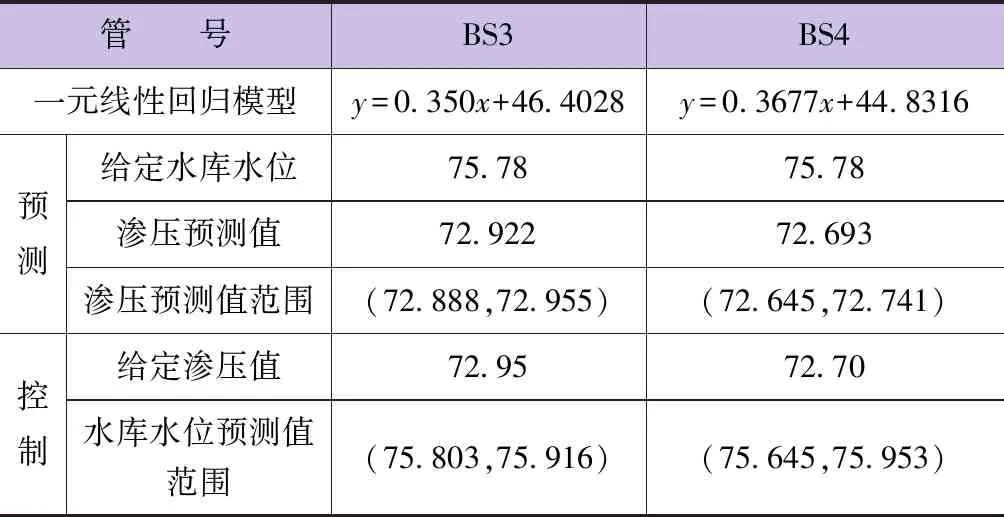
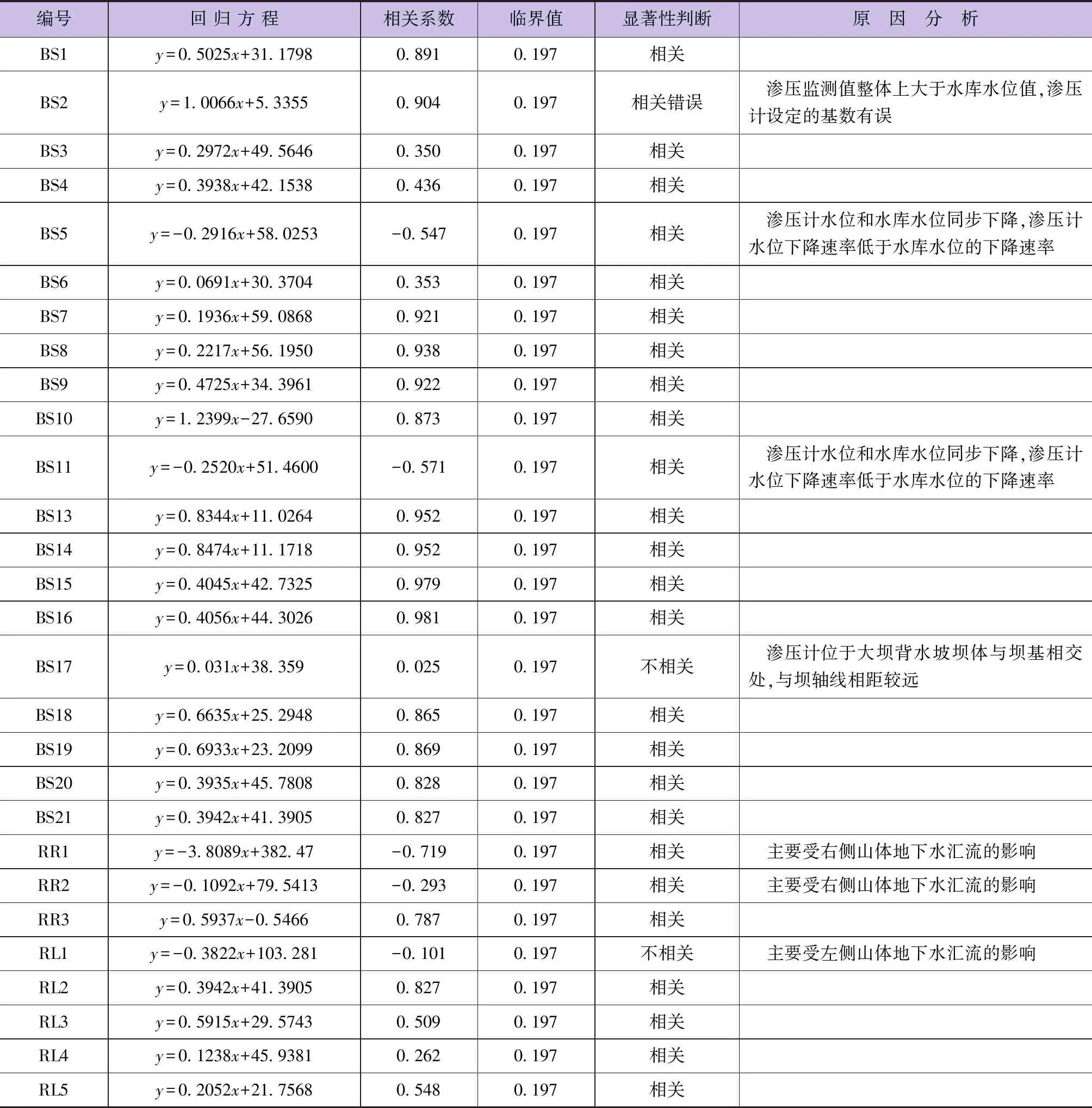
P={|t| (17) 得y0的置信度1-α的预测区间为 (18) 控制是预测的反问题,当渗压值y在某区间(y1,y2)内取值时,要求水库水位x1和x2,当x1 (20) 转化为等式方程组,求得x1和x2为 (21) 依据建立的一元线性回归模型,对于给定的水库水位和渗压值范围,预测和控制相应的预测渗压值、渗压值范围和水库水位范围,其结果见表4。 表4 回归模型预测与控制结果 模型预测结果显示,对于给定的水库水位75.78m,预测得到的渗压值分别为72.922和72.693,均在合理范围内,说明预测结果正常;预测得到的渗压值范围分别为(72.888,72.955)和(72.645,72.741),也在合理范围内。 模型控制结果表明,对BS3和BS4分别给定渗压值72.95和72.70,其1-α的置信区间均在合理范围,控制分析得到的水库水位预测值范围分别为(75.803,75.916)和(75.645,75.953),均在库水位正常运行范围内。 采用土坝渗压一元线性回归模型方法分别对东圳水库29组渗压计2019年9月1日—11月19日期间的监测数据建立了回归方程,并对监测序列中存在的异常情况进行归因分析(见表5)。由相关性分析结果可知,29支渗压计回归方程相关系数小于临界值(n=100,α=0.05)的渗压计编号为BS17、RL1。其他渗压计监测值与水库水位的线性相关性良好,相关系数最高可达0.981(BS16)。大坝渗压值与水库水位的相关性受监测点位置、地质条件、筑坝材料等多种因素影响。从监测点的位置分析,BS17渗压计所在位置为坝背水坡坝脚,离上游水库挡水边界距离较远,RL1位于大坝左右岸坝肩。受两岸山体地下水位或长距离的渗流路径影响,渗压计的数据和上游水位都有可能减弱相关性,该推论在东圳水库大坝的各渗压计回归方程相关性上得到了一定的验证。 表5 渗压监测序列相关性统计 a.依据水库水位和坝体渗压值之间存在明显的非确定相关性判断,对东圳水库两支渗压计采用最小二乘法建立渗压分析一元线性回归方程,并用相关系数法进行相关显著性检验,检验系数均在0.80以上,均大于临界值0.444,得出这两支渗压计监测值与水库水位存在显著的相关性。 b.通过对土坝渗流回归模型的预测和控制得到的两支渗压计渗压预测结果和水库安全控制水位均在合理范围,与实际测量值基本吻合。 c.经检验,东圳水库29支渗压计建立的一元线性回归模型的相关系数和显著性,总体较好,个别渗压计的异常情况原因基本查明,说明该模型方法在土坝渗压分析中是适用的。 d.本文提出的一元线性回归模型适用于稳定渗流期,鉴于渗流过程的复杂性和阶段性,今后可考虑时间、材料等多种影响因子的变化,进行多元线性回归分析。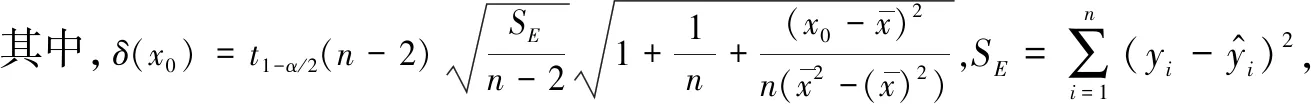
3.2 模型控制方法
3.3 预测与控制结果分析
4 模型项目应用评价
5 结 语
