基于辛普森数值微分法的成型砂轮廓形设计

黄帅可， 王战中， 孔德逊， 董文杰

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

黄帅可，王战中，孔德逊，等.基于辛普森数值微分法的成型砂轮廓形设计[J].石家庄铁道大学学报(自然科学版),2022,35(1):100-105.

双螺杆压缩机具有节能、高效、可靠性强、噪音低等明显优势，更能适应今后压缩机市场的发展需要，其市场需求将远远大于传统压缩机的增长速度，甚至在许多领域开始逐步替代传统压缩机[1-3]。双螺杆压缩机中的阴、阳转子是其关键核心部件，其加工质量的好坏直接影响着压缩机的性能。

在实际生产加工中，大多数厂家采用离散点数据的形式来表示由多段齿曲线组成的螺杆转子端面型线，但在进行砂轮廓形求解过程中，必须得先求出转子端面型线数据点处的一阶导数，求解过程繁琐。赵春秀等[4]对传统坐标计算法进一步推导得到了一种由端面数据点直接求解铣刀廓形的方法，减少了传统求解的计算量；Shen et al[5]为避免传统齿轮啮合理论中复杂的解析包络过程，提出了一种基于像素解法的成形砂轮廓形计算方法，利用数字图形扫描方法生成螺杆转子与成形刀具之间的磨削轮廓线；He et al[6]提出利用点向量包络线计算成型砂轮廓形的方法，通过点矢量在包络过程中的空间映射关系完成成型砂轮设计，避开了复杂的数值计算。这些通过复杂推导及数字方法的求解方式虽然也可以得到满足需求的砂轮廓形，但却使得求解复杂化，不便于设计及研究人员理解运用。

以加工双螺杆压缩机螺杆转子的成型砂轮为对象，在传统局部样条法确定边界条件求解一阶导数的前提下，提出利用辛普森数值微分法给定边界条件求解一阶导数并得到成型砂轮的廓形。该方法求解得到的成型砂轮廓形误差较小，无离群值，且在廓形的左右端较为光滑，为设计人员提供了参考。

1 转子螺旋面数学模型的建立

图1 螺杆转子及坐标系

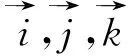
(1)

根据螺旋面的形成原理，当螺杆转子端面齿曲线τ绕z轴转过一个角度θ，且以导程T沿着z轴移动pθ时，螺旋面方程[7]可以表达为

(2)

式中,θ为角度参数，表示端面齿曲线沿着z轴转过的角度，顺着z轴看，顺时针方向为正；p为螺旋参数，表示端面齿曲线绕z轴转过单位角度时，沿着z轴方向移动的距离，其中p=T/2π。

(3)

由式(3)可以推出

nxy-nyx=pnz

(4)

式(4)为螺旋面的特性方程，是螺旋面的一个重要的性质，表示螺旋面上任意一点的坐标(x,y,z)与该点处法线坐标轴分量(nx,ny,nz)及螺旋参数p之间的关系。

2 基于离散点的成型砂轮廓形设计

图2 砂轮与转子坐标转换示意图

在实际加工中砂轮与转子的空间位置如图2所示，以转子的左端面中心为坐标原点建立转子坐标系O-xyz，使z轴与其回转轴线重合(向右为正)，x轴沿着转子与砂轮中心距方向，其正向指向砂轮轴线；在砂轮上建立坐标系Oc-xcyczc，zc轴与砂轮的回转轴线重合，xc轴与x轴重合且方向一致，yc与y轴由右手定则确定。以上2个坐标系是固定的，不随转子和砂轮运动。

转子与砂轮作相互包络运动，转子端面型线绕着转子的回转轴作螺旋运动，在某个位置时，使得转子与砂轮之间产生一条稳定的接触线C，该接触线为空间曲线。

在转子磨削加工过程中，接触线C相对于转子坐标系O-xyz是沿着z轴正方向作螺旋运动，形成转子螺旋槽；相对于砂轮坐标系Oc-xcyczc，则是接触线C绕着砂轮回转轴作回转运动，形成砂轮的三维廓形面。

如图2所示，若螺杆转子与砂轮回转轴之间的距离(中心距)为A，z轴与zc轴之间的夹角(安装角)为ω，则从转子坐标系O-xyz到砂轮坐标系Oc-xcyczc的转换式为

(5)

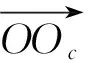
(6)

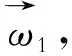
(7)

通过解除条件，整理式(6)与式(7)并通过式(4)得

nxz+nyAcotω+nz(A-x+pcotω)=0

(8)

令kx=∂xt/∂t，ky=∂yt/∂t,并将式(3)代入式(8)中，即可得到转子与砂轮的接触方程表达式

(xtkx+ytky)(xtcosθ-ytsinθ-pcotω-A)+PAcotω(kxcosθ-kysinθ)-p2θ(kxsinθ+kycosθ)=0

(9)

图3 砂轮廓形求解流程图

式(9)中A、ω和p都是常数，而其他值是关于θ的函数，所以此超越方程是关于θ的方程。通过牛顿迭代法求解该超越方程得到θ的值，将求解得到的θ代入式(2)中得到对应θ的齿面坐标点(x,y,z)，将齿面坐标点(x,y,z)代入转子与砂轮转换公式(5)中可以得到砂轮回转面上的坐标点(xc,yc,zc)，并通过式(10)表示砂轮的端面廓形，具体求解流程如图3所示。

(10)

式中,R为砂轮切削圆半径；zh为砂轮厚度。

3 接触方程中的一阶导数计算

由接触方程表达式(9)可以看出，求解θ角的关键就在于公式中的2个偏导数kx和ky，常用来求解一阶导数的方法为累加弦长参数三次曲线法[9-10]。该方法通过构造累加弦长来替代真实的曲线弧长，将对端面型线数据(xt,yt)导数的直接求解变为让xt与yt分别对弦长参数si求偏导，然后将得到的偏导数kx和ky代入接触方程表达式(9)中即可得到θ的解，进而得到砂轮的廓形。

在进行偏导数kx和ky求解前，应已知转子首末端点处的一阶导数。传统求解首末端点一阶导数为局部3次B样条曲线法，即对首末端点处先局部拟合，再对拟合曲线进行求导。该方法得到的导数精度较低，在进行后续砂轮廓形求解时，影响砂轮廓形数值的准确性。辛普森数值微分法在进行数值微分求解时具有较高的准确性，所以采用辛普森数值微分法进行首末端点一阶导数的求解，其公式[11]为

(11)

式中,y0、yn为转子端面型线首末端点的纵坐标；h为步长，h=x(2)-x(1)。

由式(11)求得首末端点一阶导数Dfirst和Dend。则累加弦长参数三次曲线法的边界条件为

(12)

令μ=hj-1/hj+hj-1,λj=1-uj,gj=6[(xj+1-xj)/hj-(xj-xj-1)/hj-1]/(hj-1+hj)，根据文献[9]可确定累加弦长参数三次曲线法的求解方程为

(13)

利用式(12)和式(13)可分别求得偏导数kx和ky，将偏导数kx和ky代入式(9)中并通过牛顿迭代法确定θ的取值，再由式(2)、式(5)和式(10)得到砂轮端面廓形坐标。

4 实例验证与分析

以某型号双螺杆压缩机阳转子为例，其中转子与砂轮几何参数如表1所示。

表1 阳转子与砂轮几何参数

分别利用局部3次B样条拟合法和辛普森数值微分法进行偏导数kx、ky和砂轮廓形的求解，并将两者计算得到的结果进行对比。表2为局部3次B样条拟合法、辛普森数值微分法和企业提供的用于实际磨削的砂轮廓形数值。

表2 2种方法及实际磨削转子的砂轮廓形值(部分) mm

图4为2种方法求得偏导数kx和ky的对比图，从图4可以看出局部3次B样条拟合法在首尾两端求解的偏导数有较大跳动，而辛普森数值微分法求解的结果在首尾两处没有较大的跳动。

图4 2种方法求解的kx和ky对比图

图5为用2种方法求解出的zh和R与企业提供的实际磨削转子的砂轮廓形数值对比的误差图。从图5可以看到用辛普森数值微分法求解的zh和R误差小且更光顺，而用局部3次B样条拟合法求解的zh和R，在砂轮廓形线两端有较大误差，需要再次处理，否则影响砂轮制造精度。

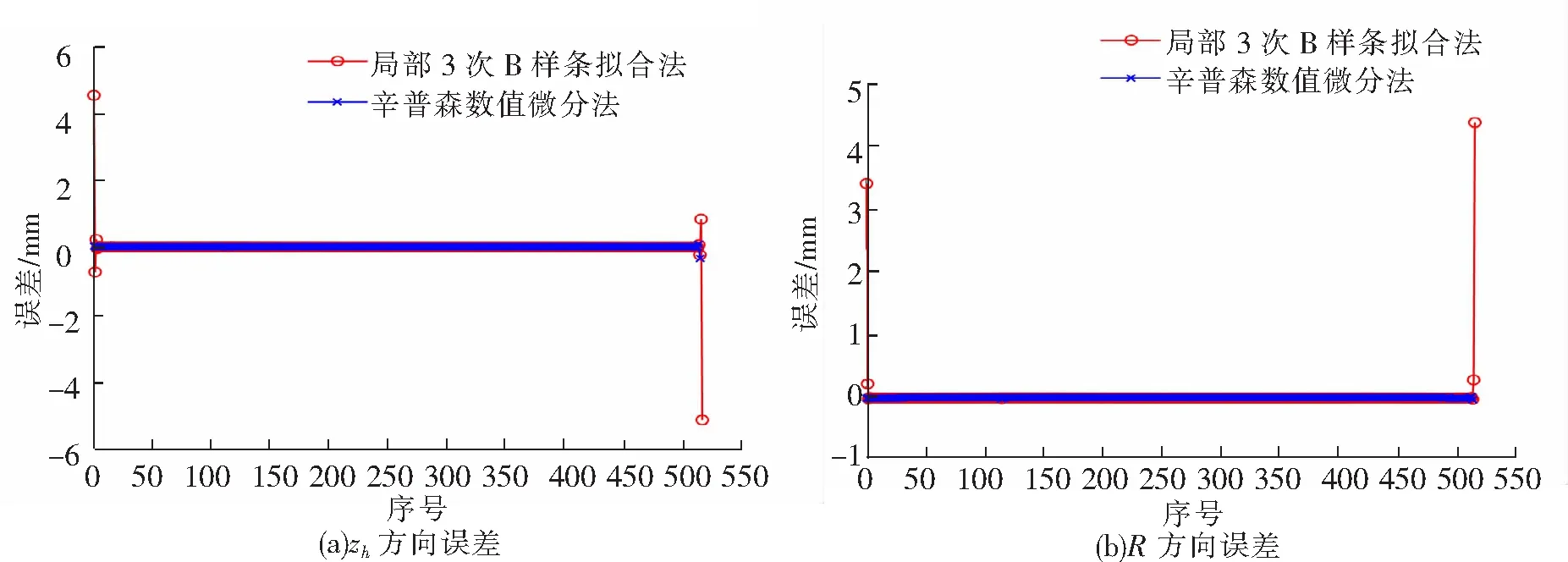
图5 2种方法在zh与R方向的误差对比图

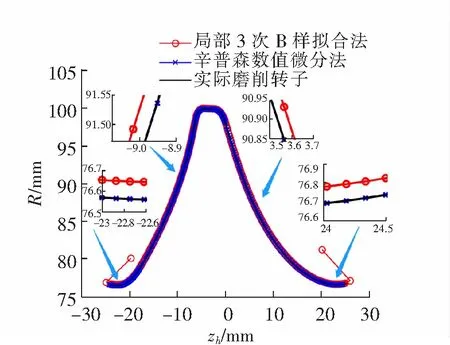
图6 2种方法与实际磨削转子的砂轮廓形对比图

图6为局部3次B样条拟合法、辛普森数值微分法及实际磨削转子的砂轮廓形。由图6可以看到辛普森数值微分法求解的砂轮廓形与实际磨削转子的砂轮廓形近乎完全重合，而局部3次B样条拟合法求解的砂轮廓形在很多位置与实际磨削转子的砂轮廓形并未重合。

为了更加准确地评估局部3次B样条拟合和辛普森数值微分法求解出砂轮廓形数值的精确度，采用可以避免误差抵消的平均绝对误差与平均绝对百分比误差来评估2种方法求解的砂轮廓形数值与实际磨削转子的砂轮廓形数值的误差。

平均绝对误差(MAE)是所有单个计算值与实际数值偏差的平均绝对值，平均绝对百分比误差(MAPE)则是平均绝对误差的百分比表示形式，两者的计算公式为

(14)

式中,Xobs为计算得到的砂轮廓形数值；Xb为实际磨削转子的砂轮廓形数值，即标准值；n为数据量总数。

通过式(14)分别计算局部3次B样条拟合法与辛普森数值微分法zh与R方向的2种误差，结果如表3所示。

表3 2种方法的误差结果

显然辛普森数值微分法zh与R方向的平均绝对误差和平均绝对百分比误差远远小于局部3次B样条拟合法，也就是说辛普森数值微分法的误差更小，其计算结果更为准确。

5 结语

以某型号双螺杆压缩机螺杆转子及转子磨削用砂轮为研究对象，基于包络法来确定螺杆转子与成型砂轮的接触条件式，分别采用局部3次B样条拟合法和辛普森数值微分法2种方法确定求解一阶导数的边界条件，借助累加弦长参数三次曲线法对接触条件式中关键的一阶导数进行求解，最终得到成型砂轮的廓形。

使用局部3次B样条拟合和辛普森数值微分法确定的2种砂轮廓形分别与企业提供的用于实际磨削转子的砂轮廓形数值进行对比。结果显示，辛普森数值微分法求解的成型砂轮廓形在光顺性和准确性上均优于局部3次B样条拟合法，这为成型砂轮的设计人员提供了重要的参考价值。

为了更加准确地评估局部3次B样条拟合和辛普森数值微分法求解出砂轮廓形数值的精确度，引入了平均绝对误差与平均绝对百分比误差，对2种方法得到的砂轮廓形数值与企业提供的用于实际磨削转子的砂轮廓形数值的误差大小进行比较。结果显示辛普森数值微分法zh与R方向的平均绝对误差和平均绝对百分比误差远远小于局部3次B样条拟合法。