基于优化残差卷积网络的滚动轴承变工况故障诊断

2022-04-12段泽森郝如江张晓锋夏晗铎

石家庄铁道大学学报(自然科学版) 2022年1期

段泽森，郝如江，张晓锋，程旺，夏晗铎

(石家庄铁道大学机械工程学院，河北石家庄 050043)

段泽森，郝如江，张晓锋，等.基于优化残差卷积网络的滚动轴承变工况故障诊断[J].石家庄铁道大学学报(自然科学版),2022,35(1):81-85.

0 引言

滚动轴承存在磨损等问题，导致各种故障的出现，很有可能会出现安全事故[1]。由于滚动轴承常被应用于变噪声和变负载共存的复合变工况中，经常出现收集到的故障信号被淹没的现象，进而导致故障的发生，使得机械设备发生非常严重的损坏[2]。因此，对复合变工况下滚动轴承运行状态的实时监测和故障诊断方法非常有理论意义和应用价值。

近些年，深度学习变得越来越热门，其算法成为人们广泛学习的对象，它利用深度网络结构对输入样本进行深层次、更全面特征提取，再经过每一层非线性激活函数实现特征的自动提取，克服了传统方法的缺陷[3-4]。利用深度学习在复杂多变的工况下对滚动轴承进行提取特征及故障识别，是未来发展的趋势，目的在于在众多干扰因素和振动信息共存情况下，能进行有效的特征提取和识别，是考验故障诊断模型稳定性的有效方法[5]。文献[6]使用改进残差网络对变工况下的滚动轴承进行故障诊断，该网络稳定性较好；文献[7]使用自适应一维卷积神经网络对滚动轴承进行故障诊断，该网络模型直接利用原始信号进行处理，最后的故障识别率达到了99%以上。但是，这些方法在模型结构与参数选择上并不是最优，这使得在处理复合变工况数据时没有较好的抗噪性和泛化性能。因此，提出了一种一维卷积与残差连接的优化模型，致力于在复杂工况下保持良好的稳定性，使得故障诊断更加精准。

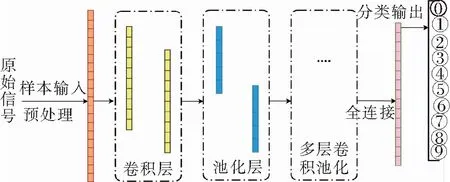
图1 一维卷积神经网络示意图

1 理论基础

1.1 一维卷积神经网络

一维卷积神经网络主要由多个卷积池化层、全连接层组成[8]，如图1所示。

卷积层主要是进行局部特征提取；池化层是通过对输入进来的特征信息进行降维、对特征进行压缩处理等；全连接层是把一个个深度处理过的局部特征进行整合，然后输入到分类器中[9]。

一维卷积公式为

(1)

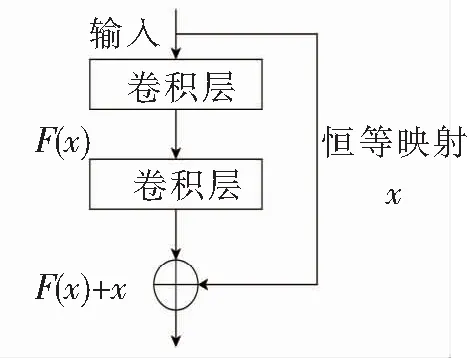
图2 残差块示意图

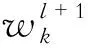
1.2 残差连接

残差神经网络(ResNet)的核心思想是引入残差模块来进行残差学习。残差块结构如图2所示，残差学习的定义为

y=F(x,{Wi})+x

(2)

式中，x、y分别为模块的输入、输出；F为将要学习的残差映射；Wi为模块参数[11]。

2 一维残差卷积神经网络模型设计

图3 一维残差卷积神经网络模型

针对滚动轴承在实际运行过程中由于变噪声、变负荷的复合工况的干扰和有效样本不足导致的故障诊断准确率低、泛化性能弱、抗噪能力差的问题，提出了一维残差卷积神经网络方法，如图3所示。其过程为：(1)一维滚动轴承振动数据输入网络输入层进行归一化预处理。(2)特征提取部分。经过卷积输出分成2部分：一部分保存为identity；另一部分继续输入到残差部分。残差部分采用了2个残差块组成，适量的残差块不仅能提高深度挖掘复合变工况中的有效特征信息能力，还能避免在训练过程中出现过拟合现象，每个残差块由多个BN层ReLU激活函数和一维卷积层组成，使用多个BN层不仅能替代池化层，还能改善梯度消失问题；加入多个ReLU激活函数能够加强池化层对故障特征信息的提取能力。2个残差块并进行2次跳跃连接构成整个残差连接部分。得到的结果再经过深层处理，最终得到提取的特征。(3)经过Dropout层、扁平层“压平”，然后通过全连接层和Softmax层进行分类。

3 实验仿真和结果分析

3.1 无负载噪声实验数据与设置

实验数据来自美国凯斯西储大学的SKF6205深沟球轴承实验台，负载为0，转速为1 797 r/min。以12 kHz频率采样，人为在内圈、外圈以及滚动体加工出不同程度的磨损，数据每个样本长度为3 000，共采用5 000个样本，根据不同的选取比例，其中训练集、测试集、验证集分别选取的数量为3 000、1 250、750。表1所示为10种工况，其中包括1种健康、9种轴承故障类型。实验所用网络结构设置如表2所示。

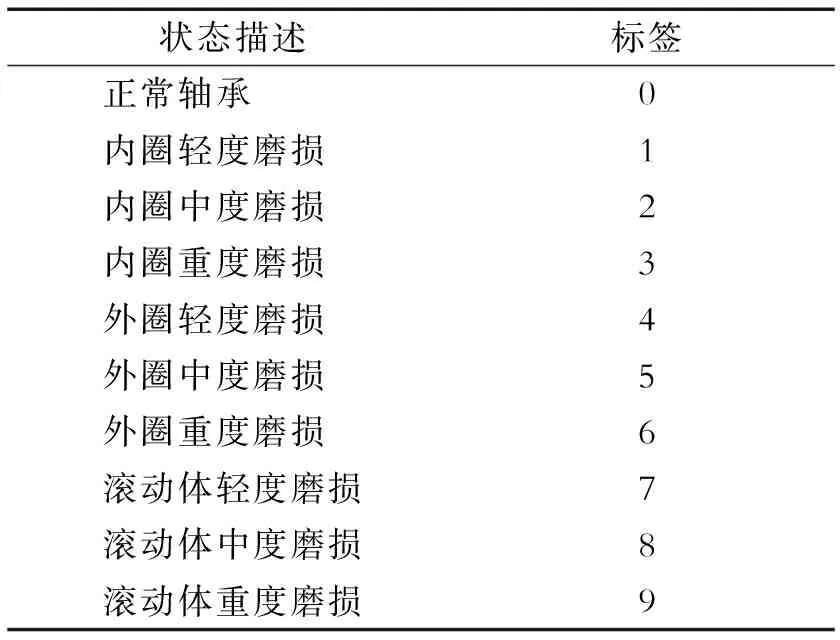
表1 滚动轴承10种故障类型

表2 参数设置

3.2 无负载和无噪声实验结果及分析

经过多次实验结果如图4所示，准确率、损失率和预测准确量分别如图4(a)、图4(b)和图4(c)。本文提出的模型利用1 250个测试样本得出的准确率为99%，损失率近乎于0.2。最后，图4(c)为预测准确量的结果，其中轻度外圈故障、重度的滚动体故障检测出错误，其他故障均能准确识别出来。

图4 实验结果

3.3 变工况实验数据与设置

在3.1节实验数据与结构设置的基础上，利用不同电机转速，选取对应的负荷数据分别为0、750、1 500、2 250 W。分别在样本中添加不同负荷和不同强度的信噪比(SNR)作为变负荷测试样本和变噪声测试样本。变工况数据的具体分类如表3所示。

表3 变工况数据

3.4 变工况实验结果及分析

3.4.1 变噪声工况故障诊断结果

图5 不同信噪比与不同模型准确率对比

滚动轴承运转过程中，零件振动以及相互摩擦会产生噪声，严重影响到轴承的运行状态。以1 500 W负荷下滚动轴承数据样本作为训练样本和测试样本。通过加入不同程度的高斯白噪声，得到信噪比为-10、-8、-5、-3、3、5、10 dB的变噪声测试样本，以检测每种方法的抗噪性，为了客观比较方法的优劣，对比实验依次使用了AlexNet、LeNet-5、一维CNN和本文方法进行对比，以上4种模型在不同噪声强度下的对比结果如图5所示。

根据图5所得，随着样本信噪比的降低，分类准确率结果明显下降，当测试样本的信噪比为-10 dB，噪声强度较强的情况下，本文方法的精度最高，达到了78.63%，LeNet-5方法精度为72.34%，而一维CNN、AlexNet方法的精度均低于60%。当样本的信噪比大于-3 dB时，本文方法、LeNet-5的方法能达到较高的精度。以上表明，与3种模型相比，本文方法具有更好的精度和更出色的抗噪声稳定性。

3.4.2 变负荷工况故障诊断结果

图6 不同方法的变负荷故障诊断结果

滚动轴承的载荷不可避免地会发生变化，因此故障诊断方法必须具有良好的泛化能力。因此，实验是在变负荷的条件下进行的，并与AlexNet、LeNet-5、一维CNN故障诊断方法进行了比较。负荷变化是指在0、750、1 500、2 250 W这4种不同的负荷数据中，用0-1、0-2和0-3分别表示在0负荷下的数据作为训练样本，以750、1 500、2 250 W负荷下的数据作为测试样本3组实验编号，其他实验组编号同理。不同方法的变负荷故障诊断结果如图6所示。

由图6可见，本文方法的故障准确率平均达到95.31%，均高于其他方法。这是因为带跳跃连接线的残差块通过构造跳跃线使得残差块增加了学习过程，通过多个卷积池化的深层处理，能够多层次和更全面挖掘特征信息。本文方法在变负荷工况条件下有较好的适应性和泛化能力。

3.4.3 复合工况故障诊断结果

设置变噪声、变负荷共存的复合工况环境，并与一维CNN方法比较，结果如图7所示。从图7(a)可得，一维CNN方法在3种不同噪声下，故障诊断准确率平均值最高为77.23%，最低为64.36%；从图7(b)可得，本文方法在3种较强噪声干扰下，故障诊断准确率平均值最高为92.32%，最低为86.73%。由此可得，本文方法的故障诊断准确率更高且平稳。